匹配Z变换完全匹配层在孔隙介质弹性波数值模拟中的应用

徐振旺

(中国石油天然气股份有限公司辽河油田分公司勘探开发研究院,辽宁盘锦124010)

真实的油气储层被认为最接近于含流体的孔隙介质,即主要由固体骨架颗粒和孔隙流体(如油、气和水等)组成。研究地震波在此类介质中的传播规律,对油气勘探开发具有重要的意义。近年来,孔隙介质弹性波传播的数值模拟研究屡有发表[1-3]。

地震波数值模拟是描述和认识地震波传播规律的主要手段之一。考虑数值模拟的计算可行性,将无限的介质区域人为地截断为有限区域,截断的边界称为人工边界。然而,人工边界的引入会导致强烈的边界虚假反射,影响数值模拟的真实性和准确性。为解决这一问题,人们研究了一系列的方法技术,主要包括两类:透射边界条件和衰减吸收层技术。

透射边界条件的本质是在人工边界处改用与原定解问题中不同的波动方程来求解全区域波场。最经典的透射边界条件是由CLAYTON等[4]提出的基于单程波动方程的旁轴近似吸收边界条件。由于该边界条件仅利用人工边界处的单层介质来吸收边界反射,故只需引入额外一层的计算量;而衰减吸收层技术则需要开辟与层数相关的内存进行计算,因此透射边界条件的计算效率相对更高。CLAYTON等提出的吸收边界条件所采用的低阶旁轴近似,能有效吸收近垂直入射的波场,但对大角度入射波场的吸收效果不佳。为提高对大角度入射波场的吸收能力,此后又发展了高阶旁轴近似吸收边界条件[5],然而高阶旁轴近似吸收边界条件要求时间步长必须满足某一条件的约束,这意味着时间递推稳定性条件变得更为苛刻,在时间域显式递推求解时需引入小时间步长,从而导致计算效率的降低。

衰减吸收层技术是在人工边界附近设置一定厚度的吸收层,使波在传播到吸收层时,按指数规律逐步衰减。目前最为成功的衰减吸收层技术是BÉRENGER[6]在求解Maxwell方程时提出的完全匹配层(perfectly matched Layer,PML)技术。理论上PML技术的吸收层内无波阻抗差异,因此反射系数为零。相较于透射边界条件,PML技术适用于较大范围入射角的地震波吸收,同时不影响时间递推稳定性条件。CHEW等[7]率先验证了PML技术在地震波数值模拟中的有效性;王守东[8]研究了PML技术在声波方程中的应用;陈可洋[9-10]提出了基于声波方程数值模拟的PML改进算法;高刚等[11]对PML的衰减因子进行了详细讨论,并对PML衰减因子的设定进行了理论研究;CHEN等[12]将PML技术应用于任意角度标量波动方程的数值模拟。上述PML研究均基于有限差分法,刘有山等[13]将PML技术应用于三角网格剖分的显式有限元地震波数值模拟。目前传统的分裂式PML技术研究较之前有所减少[14],张衡等[15]完成了分裂式的PML在TTI介质声波方程模拟中的加载;马锐等[16]提出在伪谱法弹性波模拟中使用SPML和海绵边界的混合边界条件,并取得了良好的吸收效果。

近20年来,PML技术不断改进,其中较为成功的改进技术是将经典PML中的复数坐标变换为复频移拉伸算子[17],称之为复频移拉伸(complex frequency shifted,CFS)PML(CFS-PML)技术。相较于传统的PML,CFS-PML能更有效地吸收近似掠射的入射波;非分裂形式的CFS-PML无需进行波场分离,可节省计算机内存。目前,非分裂形式的CFS-PML实现方法主要有卷积法(convolutional PML,CPML)[18]、积分法[19]和辅助微分方程法[20]。其中CPML应用广泛,最初应用于求解Maxwell方程组,而后逐步应用于地震波数值模拟[21-25]。MARTIN等[26]率先将CPML应用于一阶Biot方程的时间域有限差分法求解;HE等[27]对二阶Biot方程的有限元法求解提出了一种新的非分裂形式PML,并借助COMSOL软件平台讨论了其吸收效果。值得关注的是,SHI等[28]基于CFS-PML提出了一种匹配Z变换(matched Z-transform)PML(MZT-PML)技术,并将其应用于弹性波数值模拟。MZT-PML继承了CFS-PML所有优点,而采用Z变换技术使MZT-PML相比CPML能更直接地实现复频移拉伸算子,因此MZT-PML技术可被进一步应用于粘滞声波方程数值模拟[29]。

本文采用时域交错网格有限差分法,将MZT-PML技术扩展应用于孔隙介质弹性波传播的数值模拟,然后给出了在Biot方程加载MZT-PML的一般推导过程,最后通过数值模拟算例证明了MZT-PML技术的有效性。

1 方法原理

1.1 孔隙介质弹性波动方程

二维孔隙介质弹性波波动方程表示如下[30]:

式中:自由指标i和j在二维情形下分别可取x或y;哑指标k遵守爱因斯坦求和法则;δij表示Kronecker函数;μ表示剪切模量;λs=λ-α2M表示固体骨架的拉梅系数,其中λ表示饱含流体骨架的拉梅系数。

1.2 匹配Z变换完全匹配层

将(1)式和(2)式写成二阶位移格式和一阶速度-应力格式,并变换到频率域,有:

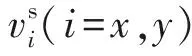
KUZUOGLU等[17]对(4)式进行改进并提出了如下的复频移拉伸算子(CFS-PML边界条件下),改善了大角度入射波的吸收效果:

式中:衰减参数dη,κη和αη均表示沿η坐标轴的实函数,具体公式见后文,dη≥0,κη≥1,αη≥0,其中η为自由指标,在二维情形下分别可取x或y。当κη=1和αη=0时,CFS-PML退化为传统的PML。将PML的复拉伸坐标代入(3)式中的第1个方程(第2个方程的处理跟第1个方程的处理过程相同,不再赘述),可得:

(5)式为关于频率的函数,如果将(6)式和(7)式进行傅里叶反变换到时间域,得到的波动方程将会产生卷积项。CPML的基本原理即为引入记忆变量,并采用递推卷积技术来计算卷积项,从而实现复频移拉伸算子的加载。我们注意到无论是时间域中的卷积或者频率域的乘法运算在Z域均简化为乘法运算,于是将(6)式和(7)式变换到Z域能相对容易地应用CFS-PML技术,这便是本文所采用的MZT-PML技术的基本思想。

MZT-PML在Biot方程中实现复频移拉伸算子的基本推导过程如下。将(5)式的复频移拉伸算子变换到Z域,同时将式中所有速度-应力方程变换到Z域。首先考虑(5)式在S域的倒数形式为:

式中:s表示复频率参数。对于任意变量P,从S变换到Z变换有如下对应关系:(s-P)↔(1-ePΔtz-1),故(8)式对应的Z变换结果为:

式中:Δt表示时间采样间隔。考虑到(1-z-1)/Δt为iω的Z变换,那么(6)式的Z域形式可表示为:

(11)式,(12)式和(13)式可进一步改写为:

其中,中间变量bη=e-(αη+dη/κη)Δt(η=x,y)。将(11)式、(12)式和(13)式代入(10)式,可得:

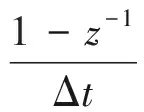
Ψσxy,y-ayz-1Ψσxy,y)+ρf(ΨPf,x-

axz-1ΨPf,x)+ρfKvfx

(17)

式中:aη=e-αηΔt(η=x,y);考虑到z-1表示离散时间域一个步长的延迟,那么(14)式、(15)式、(16)式和(17)式可以表示为如下的有限差分时间递推格式:

(21)

(18)式、(19)式、(20)式和(21)式即为包含了MZT-PML的时间域有限差分递推式。对于(3)式中的其它方程采用同样的方法处理即可以完成MZT-PML的加载,然后对这些方程采用空间四阶时间二阶交错网格有限差分法离散求解,则可算出全部分量的波场。

2 数值模拟及分析

为验证MZT-PML技术在孔隙介质弹性波数值模拟中的有效性及长时间模拟的稳定性,设计如图1 所示的均匀孔隙介质模型进行数值模拟实验。将得到的数值结果与参考解进行对比分析,并与采用CPML技术得到的数值解进行比较分析,以验证MZT-PML技术的可靠性。

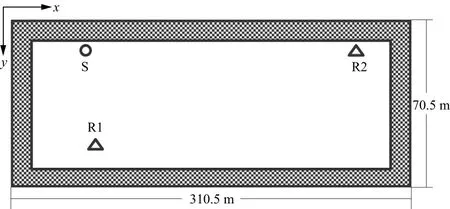
图1 二维均匀孔隙介质模型

均匀孔隙介质弹性波数值模拟包括两部分,图1中的阴影部分为MZT-PML吸收层区域,中间的空白部分为求解区域,模型为长条状,有利于检验MZT-PML吸收层对近似掠射入射波的吸收效果。圆圈S为震源激发位置,坐标为(30m,5.5m),震源为固相纵波源,主频为80Hz,三角形R1和R2为接收点,坐标分别为(40m,60m)和(300m,5.5m),该均匀孔隙介质模型的物性参数如表1所示。模型大小为310.5m×70.5m,空间离散时,x方向和y方向的相邻网格点间距均为0.5m,全区域离散网格点为622×142个。依据时间递推稳定性条件[26],时间步长应小于0.11ms,故此处设定时间步长为0.1ms,采样时间长度为600ms,时间采样点为6000个。MZT-PML吸收层的厚度为5m,包含10个有限差分单元。将震源置于顶部吸收边界附近,接收点R1和R2置于底部和顶部吸收边界附近。MZT-PML吸收层的吸收效果受衰减参数dη、κη和αη的控制。这3个衰减参数通常由以下3个公式确定[31]:

式中:η表示PML吸收层内一点到交界面的距离;L表示PML吸收层的厚度。本算例中,各衰减参数取值如下:dmax=-(pd+1)cplg(Rc)/2L,amax=πf0,κmax=-(pκ+1)blg(Rc)/2L,其中,Rc=10-5,pd=pκ=2,pα=1,b=10Δh,Δh为差分网格点最大间距,cp表示最大纵波速度,本算例中为快纵波速度;f0为子波主频。

表1 均匀孔隙介质模型的物性参数

图2为均匀孔隙介质模型加载MZT-PML后数值模拟得到的40ms,100ms和200ms时刻的波场快照。图2a和图2b分别为40ms,100ms和200ms时刻固相和流相的x分量,图2c和图2d分别为40ms,100ms和200ms时刻固相和流相的y分量。可以看出,MZT-PML技术对各个角度的入射波场都有良好的吸收效果。对比图2中固相和流相的波场快照,可发现慢纵波振幅比快纵波振幅大(波前超前的为快纵波,滞后的为慢纵波),流相和固相中的慢纵波相位相反,流相中的快纵波振幅相对更小,这种振幅上的差异导致图2b和图2d中并未显示出快纵波。

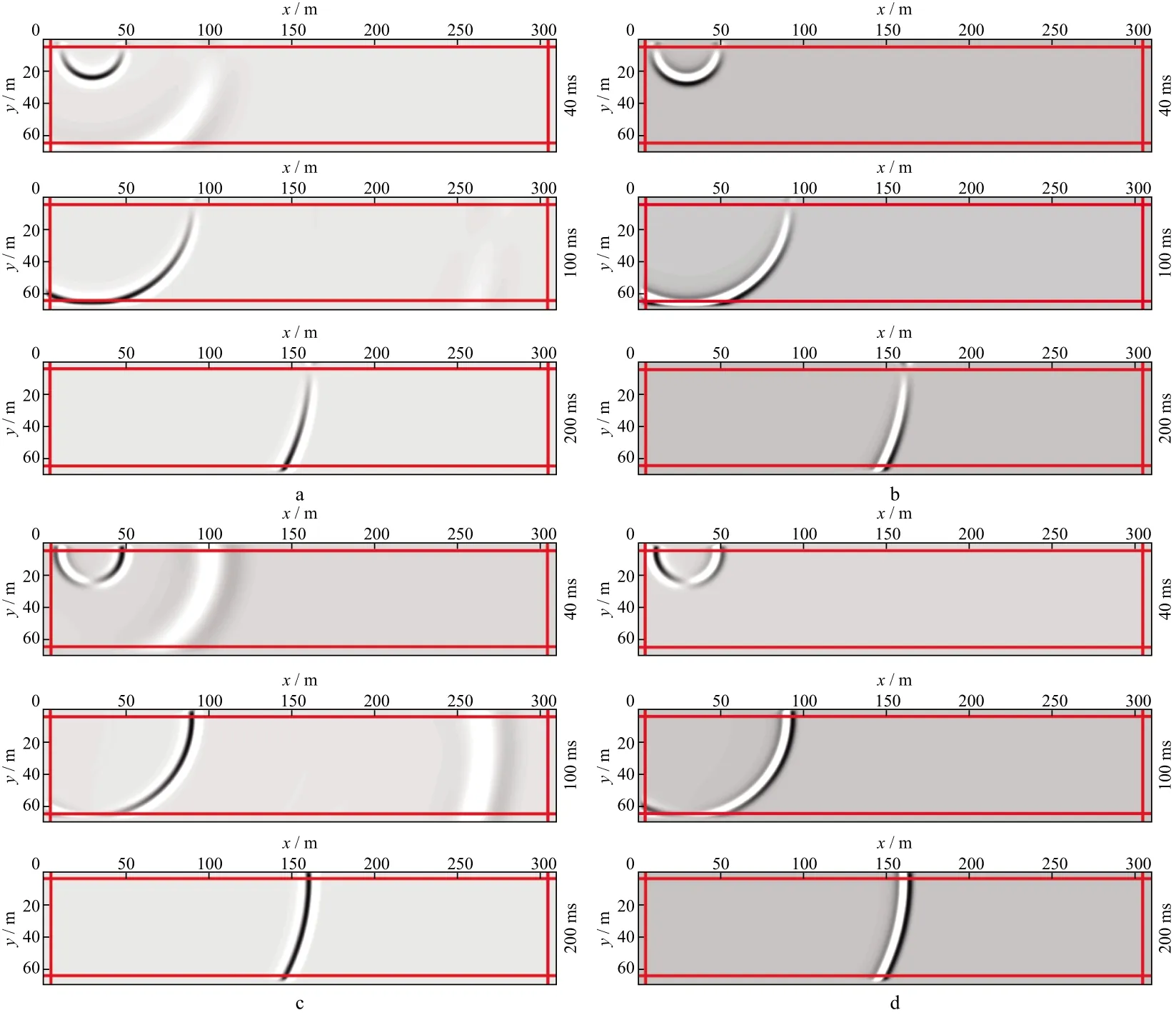
图2 固相x分量(a)、流相x分量(b)、固相y分量(c)和流相y分量(d)在40ms,100ms和200ms时刻的波场快照(红色直线表示MZT-PML吸收层的内边界)

图3和图4分别为CPML和MZT-PML边界条件下接收点R1和R2处的固相x分量记录,其中的参考解利用扩边方法获得。从图3a可看出,CPML和MZT-PML边界条件下得到的数值解与参考解高度吻合,且拟合误差在10-2量级,说明CPML和MZT-PML边界条件下近垂直方向入射波吸收效果好。图3b 为CPML和MZT-PML边界条件下得到的数值解和参考解的差值对比,可以看出二者仅存在微小的差异,这是CPML和MZT-PML边界条件的离散格式差异造成的。图4进一步展现了CPML和MZT-PML边界条件下近似掠射的入射波吸收效果,CPML和MZT-PML边界条件下得到的数值解与参考解几乎完全吻合,说明CPML和MZT-PML边界条件下近似掠射的入射波均吸收效果好。

长时间数值模拟的稳定性也是评价各种完全匹配层的重要指标之一。图5显示了CPML和MZT-PML边界条件下波场总能量随时间的衰减情况。波场总能量的计算公式如下[26]:

式中:点号表示对时间的一阶偏导。本算例中将传播时间延长至10s,即10000倍时间步长,传播时长分别为0.6s和10.0s时波场总能量衰减情况如图5所示。由图5a可见约0.4s之后能量陡降,这是因为此时直达波完全离开了求解区域;0.4s之后能量逐渐趋于稳定,理论上此时残留的能量全部为虚假反射能量。由图5b可知即使是在6.0s之后,能量仍呈微弱的下降趋势,说明了MZT-PML和CPML边界条件均具有较好的长时间数值模拟稳定性,经MZT-PML和CPML边界条件吸收后残留的总能量基本处于同一数量级。

图3 CPML和MZT-PML边界条件下接收点R1处的固相x分量记录a 数值解与参考解对比; b 数值解与参考解的差值对比

图4 CPML和MZT-PML边界条件下接收点R2处的固相x分量记录a 数值解与参考解对比; b 数值解与参考解的差值对比

图5 CPML和MZT-PML边界条件下不同传播时长的波场总能量衰减情况a 传播时长0.6s; b 传播时长10.0s

3 结论

本文详细推导了非分裂MZT-PML在Biot方程中实现复频移拉伸算子的一般过程,并采用时域交错网格有限差分法对加载了MZT-PML的Biot方程进行离散求解。与基于傅里叶变换和卷积算子的CPML不同的是,采用匹配Z变换技术的MZT-PML可更直接地实现复频移拉伸算子。数值模拟结果表明,MZT-PML对孔隙介质中固相和流相的各分量均具有良好的吸收效果。与CPML类似,MZT-PML也能有效吸收各个角度入射的地震波,尤其对于近似掠射的入射波的吸收效果显著。由长时间能量衰减计算结果可知,MZT-PML在Biot方程求解中具有长时间数值模拟稳定性。