薄层反透射系数关于射线参数的低阶近似

杨 春,陈本池,翟冠宇,时 磊

(1.中国地质大学(北京)地球物理与信息技术学院MWMC研究组,北京100083;2.中国石油化工股份有限公司科技部油田处,北京100728;3.中国石油化工股份有限公司石油勘探开发研究院,北京100083)

在我国,无论是油气勘探较为成熟的东部地区,还是勘探程度相对较低的西部各大盆地,岩性油气藏逐步成为油气勘探的主要对象之一。对我国陆相沉积盆地而言,岩性油气藏的地层厚度一般低于常规地震勘探的垂向分辨率,以薄层的形式存在[1]。我国煤系地层厚度多在2～10m,且常以薄层的形式存在,反射响应非单一界面产生,而是顶底反射、层间多次波叠加而成的复合波[2]。因此,研究薄层地震反透射理论,对油气、煤炭等资源的开发具有一定的理论及现实意义。

对薄层反射透射的理论研究可追溯到20世纪60年代。布列霍夫斯基赫等[3]从弹性波动力学理论的角度讨论了平面波在层状介质中的反射和透射情况,建立了传播矩阵方法;之后WIDESS[4]忽略层间多次波及转换波的影响,建立薄层反射振幅与薄层厚度的关系式;KENNETT[5-6]给出球面波入射情况下层间反射系数的递归关系;汪恩华等[7-8]给出纵波入射和全固态介质假设条件下薄层的反透射公式,并进一步给出单个薄层垂直入射时的纵波反射系数谱计算公式;21世纪后薄层反射理论研究发展迅速,郭智奇等[9]结合薄层反射动力学及粘弹性理论研究了薄储层物性与AVO属性的关系。YANG等[10]给出薄层厚度较小时单薄层反透射系数的拟Zoeppritz矩阵方程,并给出小角度及弱阻抗差前提下的单薄层PP波反射的近似解析表达式,但该近似式忽略了层间转换波及多次波的影响[11];张军华等[12]梳理了薄层叠后地震解释技术,建立了多个模型并对其效果进行了评述;彭军等[13]使用基追踪方法识别薄层模型并在实际油气田中检测应用效果;马跃华等[14]建立了“岩性组合-阻抗组合-地质成因”的多维度薄层分类标准,并以大港油田的两个应用研究为例,分析了薄层的地震响应特征;杨春等[15]结合Gassmann方程与薄层反射透射矩阵方程分析了含油气薄砂储层的地震反射特征。以上研究在很大程度上推动了薄层反透射理论的发展,然而,所给出的薄层反透射系数公式有些需要进行复杂的矩阵运算,有些忽略了层间多次波及转换波的影响,对薄层AVO分析及反演具有一定的局限性。

由于薄层精准反透射系数方程较为复杂,无法直接应用于实际的薄层反演,因此,需要给出形式较为简洁的近似公式。参照单界面反透射系数近似的研究方法[16-18],本文讨论了薄层反透射系数与射线参数的关系,对薄层转换波和非转换波与射线参数的奇偶关系予以证明,并给出薄层反透射系数的低阶近似形式。在此基础上,分别对给定的两类典型薄储层模型(强阻抗差薄层、弱阻抗差薄层)的反射系数精确解与低阶近似解进行了误差分析,讨论了小角度范围内(≤30°)射线参数高次项舍弃的可行性与舍弃后的低阶近似精度。

1 薄层反透射系数与射线参数的关系

P波入射时,薄层反透射系数矩阵可写为:

其中,RPP,RPS,TPP和TPS分别为薄层PP波和PS波的反射和透射系数;mij为反透射系数矩阵方程组的系数矩阵元素;ni为反透射系数矩阵方程组的常数项列矩阵元素;mij和ni由目标薄层的弹性参数、薄层厚度、入射波频率、入射角决定,具体表达式见参考文献[19]。

将入射角记为θ,且3层介质中纵波传播方向与法线的夹角分别记作θ1,θ2,θ3,横波传播方向与法线的夹角分别记作δ1,δ2,δ3。根据Snell定律,有:

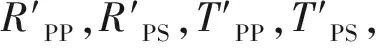
比较(1)式和(3)式,可以看出:

由此可知,薄层非转换波的反射和透射系数是sinθ(或射线参数)的偶函数,而转换波的反射和透射系数是sinθ(或射线参数)的奇函数。

利用反射和透射系数的奇偶性可以将其表示成以下sinθ的幂级数形式:

式中:AR2n,AR2n+1,AT2n,AT2n+1分别为薄层PP波

反射系数、PS波反射系数、PP波透射系数及PS波透射系数的幂级数展开式的系数。入射角较小时,sinnθ随着级数n的增大而迅速衰减,则近似求解出参数AR2n,AR2n+1,AT2n,AT2n+1,并根据精度需求对(5)式进行高阶舍弃,从而获得相应的薄层反射或透射系数的近似公式。

2 薄层反射系数的低阶拟合

针对油气及煤资源勘探面临的薄储层模型,我们分别建立了强、弱阻抗差的薄层模型,并讨论n≤1情况下两种模型的反射系数低阶近似与精确解的差异。表1给出了强阻抗差的薄煤层和弱阻抗差的含油气薄砂岩层的模型参数。设定入射纵波主频为50Hz,计算小角度范围内(入射角θ≤30°)不同厚度下薄层PP波、PS波的反射系数。薄层厚度依次取值为:λ/4,λ/8,λ/10,λ/20,λ/30,λ/40,λ/60,λ/80,λ/100,0,其中,λ为纵波波长,0代表薄层上覆围岩及下伏围岩构成的单界面特例,顶界面、底界面分别代表薄层顶界面、底界面的反射情况。鉴于薄层反射系数为复反射系数,而实际地震勘探中接收到的为实地震信号,所以以下仅对薄层反射系数的实部进行讨论。对PP波反射系数的实部进行sin2θ线性拟合,PS波反射系数的实部进行sinθ线性拟合,并与薄层顶、底界面反射系数情况进行对比。

图1至图3给出了不同厚度下含油气砂岩模型的RPP关于sin2θ的线性拟合结果。由图1至图3可以看出,随着薄层厚度的减小,含油气砂岩层的RPP实部随sin2θ的增加其变化趋势发生改变:当薄砂层厚度小于等于λ/10时,RPP的实部随sin2θ的增加而减小,与薄层顶界面和底界面反射系数的实部随sin2θ的变化规律一致,说明在此厚度范围内,顶界面与底界面的阻抗差对反射系数的影响较大;厚度大于等于λ/8时,RPP的实部随着sin2θ的增加而增大。当入射角θ≤30°时,薄层反射系数RPP的实部对sin2θ线性程度很高,特别是厚度范围为(λ/60,λ/20)时;λ/8和λ/10为RPP实部随sin2θ的增加而变化趋势发生改变的界限点,反射系数的实部随sin2θ变化的线性程度较其它厚度低,但对sin2θ线性拟合的确定系数R2也大于等于0.910。薄煤层模型呈现规律大体上与薄含油气砂岩一致,考虑篇幅限制,我们只给出了含油气砂岩层模型的RPP实部部分厚度的拟合图。图4给出了两个模型不同厚度及顶、底界面反射系数线性拟合(RPP的实部关于sin2θ的线性拟合,RPS的实部关于sinθ的截距为0的线性拟合)的确定系数R2。由图4可以看出,含油气砂岩层模型厚度为λ/10的RPP实部拟合的确定系数最小,但也高达0.912。说明在小角度范围(入射角≤30°)内,不论是强阻抗差的煤层模型还是弱阻抗差的含油气砂岩模型,反射系数在n≤1情况下的拟合程度都很高(R2≥0.912)。

表1 薄煤层和薄砂层的模型参数

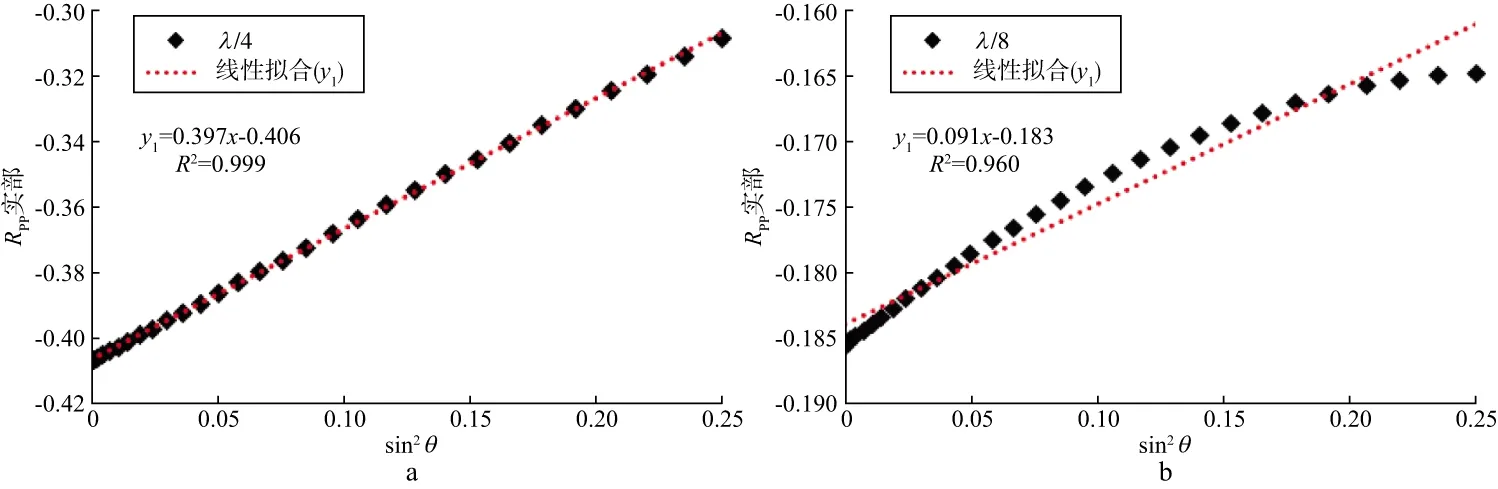
图1 厚度为λ/4(a),λ/8(b)的含油气砂岩模型的RPP关于sin2θ的线性拟合结果

图2 厚度为λ/10(a),λ/20(b),λ/30(c),λ/40(d),λ/60(e),λ/80(f),λ/100(g)的含油气砂岩模型的RPP关于sin2θ的线性拟合结果

图3 厚度为0(a)及顶(b)、底(c)界面含油气砂岩模型的RPP关于sin2θ的线性拟合结果

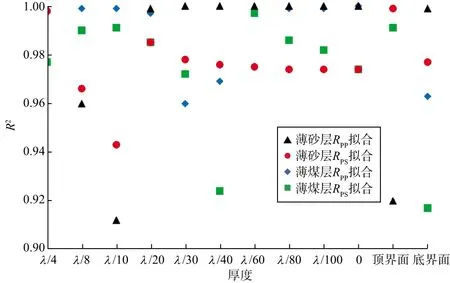
图4 不同厚度下反射系数的确定系数R2

将拟合曲线斜率记为G,截距记为P,计算不同厚度下薄层与薄层厚度减至0时上覆围岩与下伏围岩组成的单界面、薄层顶界面、薄层底界面的反射系数关于|ΔG|及|ΔP|的相对变化(图5)。由图5可以看出,对于含油气砂岩层模型,当薄层厚度较大时(λ/4,λ/8,λ/10),反射系数的实部更接近于顶界面情况,说明薄层与上覆围岩介质参数对薄层反射系数的影响较大;当厚度较小(λ/20,λ/30,λ/40,λ/60,λ/80,λ/100)时,反射系数的实部更接近于薄层厚度为0时的情况,即薄层上、下围岩的介质参数共同影响薄层反射系数。由于λ为纵波波长,而横波波长(λS)满足:λ/8<λS/4<λ/4,因此,对横波而言仅考虑厚度小于等于λ/8的情况:薄层厚度较大(λ/8,λ/10)时,RPS的实部更接近于顶界面情况;薄层厚度较小(λ/20,λ/30,λ/40,λ/60,λ/80,λ/100)时,RPS的实部更接近于薄层厚度为0时的情况。对于煤层模型计算结论与含油气砂岩层模型相似。

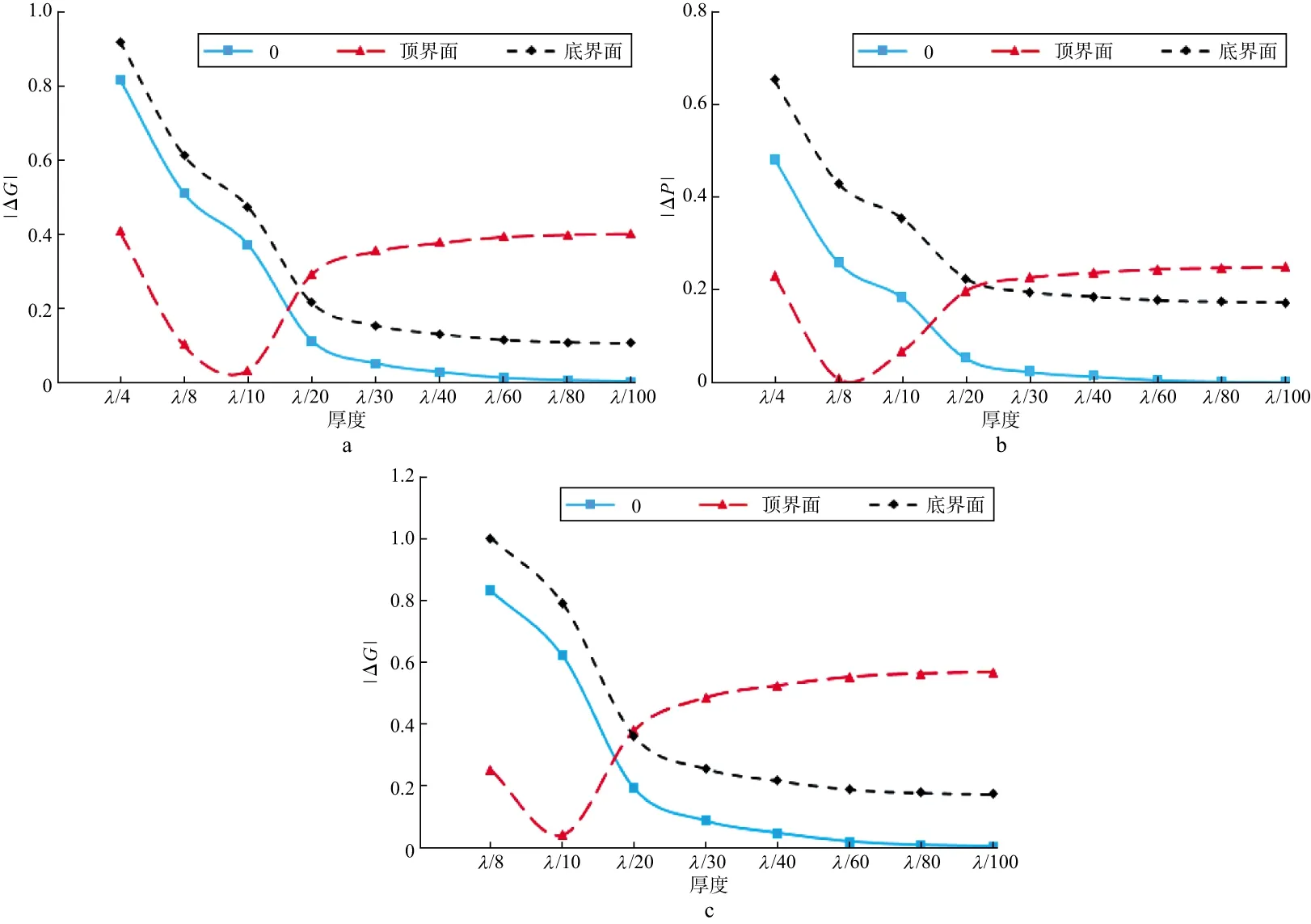
图5 不同厚度下含油气砂岩模型相对不同界面的RPP,RPS关于|ΔG|及|ΔP|的变化情况a RPP关于|ΔG|的相对变化; b RPP关于|ΔP|的相对变化; c RPS关于|ΔG|的相对变化

3 讨论与结论

利用反射和透射系数的奇偶性可以将其表示成sinθ的幂级数形式,薄层非转换波的反射和透射系数是sinθ(或射线参数)的偶函数,而转换波的反射和透射系数是sinθ(或射线参数)的奇函数;级数n≤1情况下两种薄层模型的反射系数低阶近似与精确解的拟合结果说明,对薄层PP波反射系数的实部进行sin2θ线性拟合、PS波反射系数的实部进行sinθ线性拟合,都可以获得较高的拟合精度;薄层上覆、下伏围岩的介质参数对薄层反射系数的影响较大。

本文仅给出了薄层转换波及非转换波反透射系数与射线参数的奇偶性关系,公式(5)中参数AR2n,AR2n+1,AT2n,AT2n+1的具体表达式并未给出,需要进一步研究给出完整的反透射系数表达式,并根据精度需求对公式(5)进行高阶舍弃获得相应的薄层近似公式。在下一步薄层AVO属性分析中,可以利用以上结论绘制薄层AVO的PG交会图,以获得薄层属性。本文仅讨论了煤层和含油气砂岩层模型,在未来地震勘探中还需要讨论更多薄层模型得到普适性的结论。