泡泡形成的理论和实验探究
王心华,卢博文,潘晓军,刘 斌,高秀平
(兰州大学 a.物理学国家级实验教学示范中心;b.物理科学与技术学院,甘肃 兰州 730000)
泡泡的形成在生活中非常常见,形成的液体泡泡对工农业生产将会产生一定的影响. 目前国内外学者对于泡泡如何形成的理论及应用进行了一定的研究[1-3]. 本文在此基础上,对泡泡的形成过程进行了初步的理论探究,并发现其和实验结果拟合较好,说明理论对该现象可以进行很好的解释,其研究结果对泡泡形成的认识具有一定的指导价值.
1 实 验
1.1 实验装置
为了研究泡泡的形成过程,了解喷嘴喷出的气流作用在肥皂膜上的物理机制,搭建了如图1所示的实验装置. 实验使用40 L的高压氮气和高压氩气作为气源,以此控制气体流速恒定,并通过减压阀的旋钮开关控制流速的大小;使用PU导气管,中间接入MF5712-200型流量计用来测量瞬时流量;用透明胶固定管子,保证管子尽量排列在一条直线上,以减小因管子弯曲而产生额外湍流,并且保证喷口水平;使用3D打印机打印需要尺寸的泡泡环,并将制作好的泡泡环固定在架子上,泡泡环和喷口之间的距离可以调节,如图2所示;拍照和摄像分别使用单反相机和高速摄像机;购买市面上常见的泡泡液作为实验原料.

图1 实验装置的整体图

图2 泡泡环的放置装置
1.2 实验参量
在实验中,控制流速v在0~60 m/s可调,使用毛细管法测量肥皂液的表面张力系数[4-5],其数值γ为2.78 ×10-2N/m,使用密度计测量泡泡液的密度ρ为1.005 g/cm3,氮气的密度ρN2和氩气的密度ρAr分别为1.25 g/L和1.78 g/L.
1.3 预实验
为了探究流速和泡泡膜间的关系,使用直径为8 mm的PU管,制作内径为6.67 cm、外径为10.00 cm的泡泡环进行预实验. 实验中,通过控制减压阀让流量从小开始不断增大,拍摄到如图3~4所示的实验现象.

图3 当流速不断增大时“坑”的演化

图4 速度大于阈值时吹出泡泡的情景
分析图3可以得出,向泡泡膜通气时,如果控制流速在一定范围内时,膜会逐渐向外突出,形成一个类似于“坑”的结构,靠近泡泡环的地方是一个宽度基本均匀的圆柱体,最外侧为一曲面,若流速不变,“坑”只会轻微抖动,直到厚度小于临界厚度后破裂[6]. 随着流速的不断增加,圆柱体的长度不断增加,宽度也随着增加,最外侧曲面的曲率半径减小. 当流速达到某一阈值vc时,“坑”将不再变化,而当流速大于阈值vc时,“坑”的末端将从某点处收缩,然后断裂形成一个泡泡,之后重复这一断裂过程,如图4所示. 为了研究阈值与具体相关物理参量间的关系,建立了简单的模型.
2 理论模型及实验验证
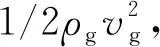
2.1 喷嘴靠近泡泡环,即x=0的情况
先考虑包含的情况,即R(x)≤b/2,实验发现,速度达到阈值时,产生的泡泡的曲率半径κ-1和R0近乎相等,所以此时的受力平衡方程为
(1)
从此推导出速度的阈值表达式为
(2)
而对于不包含的情况,即R(x)>b/2,Salkin L进行了比较详细的研究[10],他的研究工作表明:由于泡泡环的限制,当气体流速达到阈值时泡泡的曲率半径不再由半径决定,而是由泡泡环的宽度决定,泡泡环的宽度限制了泡泡的增大,即流速达到阈值时,κ-1=b/2,这时流速阈值为
(3)
2.2 喷嘴远离泡泡环,即x>0的情况
当喷嘴离泡泡环有一定距离时,喷嘴喷出的气流在到达泡泡环的途中会进行一定的演化,这是一个射流问题[11]. 如图5所示,喷出的气体成一圆锥形,张角为θ,因此,在喷嘴离泡泡环为x处的射流半径可修正为
(4)
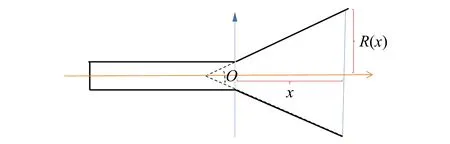
图5 射流示意图
由射流问题可知在x处时,射流速度的分布沿着径向为高斯分布[12-13]. 为了验证这个分布,使用AR-866A热线风速仪测量风速的空间分布,得到了在x处沿径向各个r处的风速值,将数据导入Origin并用高斯函数进行非线性拟合,如图6所示.
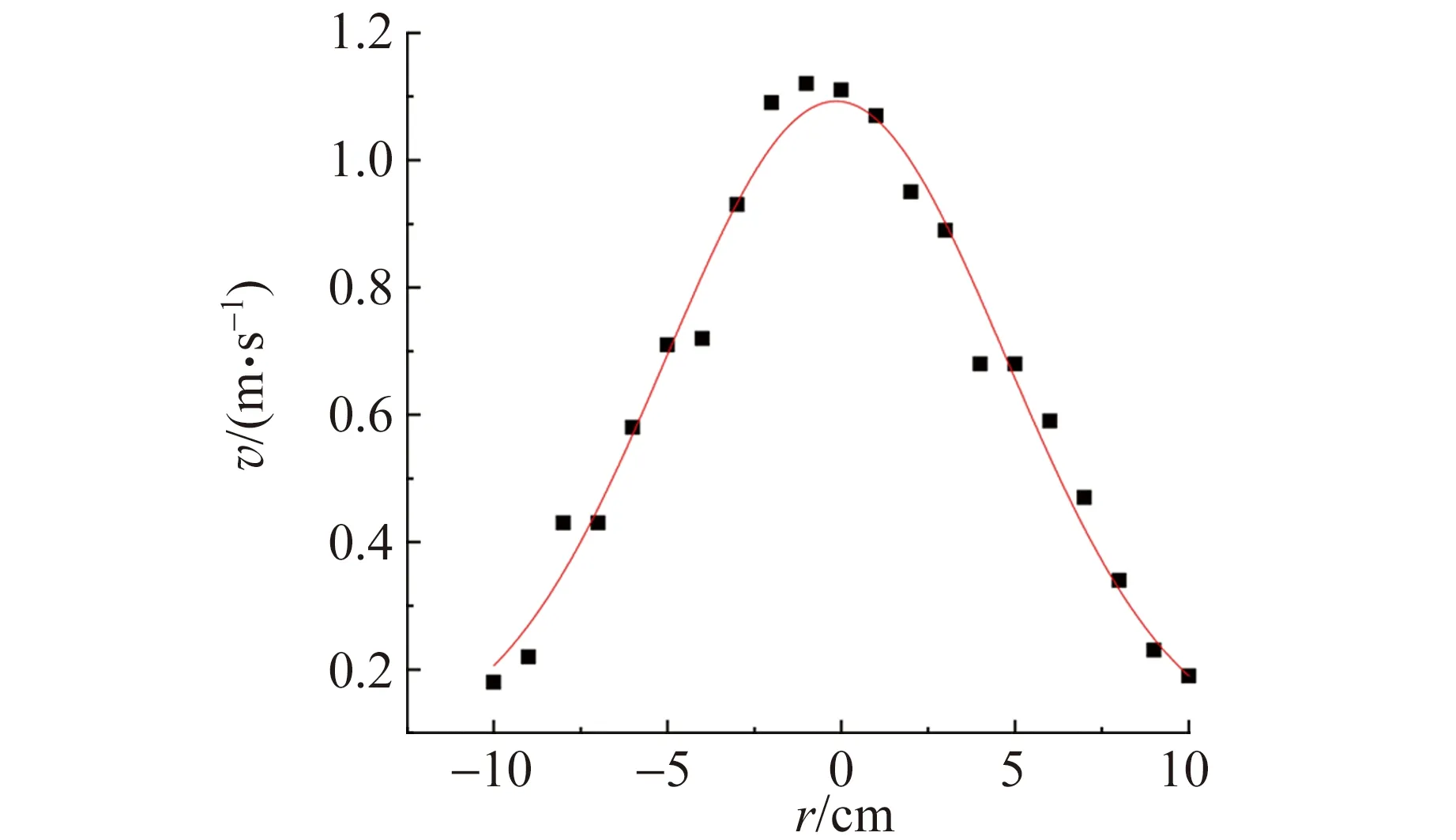
图6 径向气流分布图
从图6中得到实验数据的相关系数为0.977 49,拟合程度很高,所以气流速度在径向上确实是高斯分布,故气体流速为
(5)
已知高斯分布下总面积的95%对应于宽度4σ(x). 假设该宽度等于x处的射流直径,即4σ(x)=2R(x),则由式(4)得出标准偏差是距离x的线性函数为
(6)
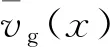
(7)
由式(7)可以推导出
R(x)vmax(x)/2=R0vg,
(8)
实验发现流速不同,θ值不同,考虑这是由于速度不同时雷诺数不同所导致的,当低速时流体可近似看成层流,θ很小;而当流速过高时流体应为湍流,有着很大的θ,如图7所示.
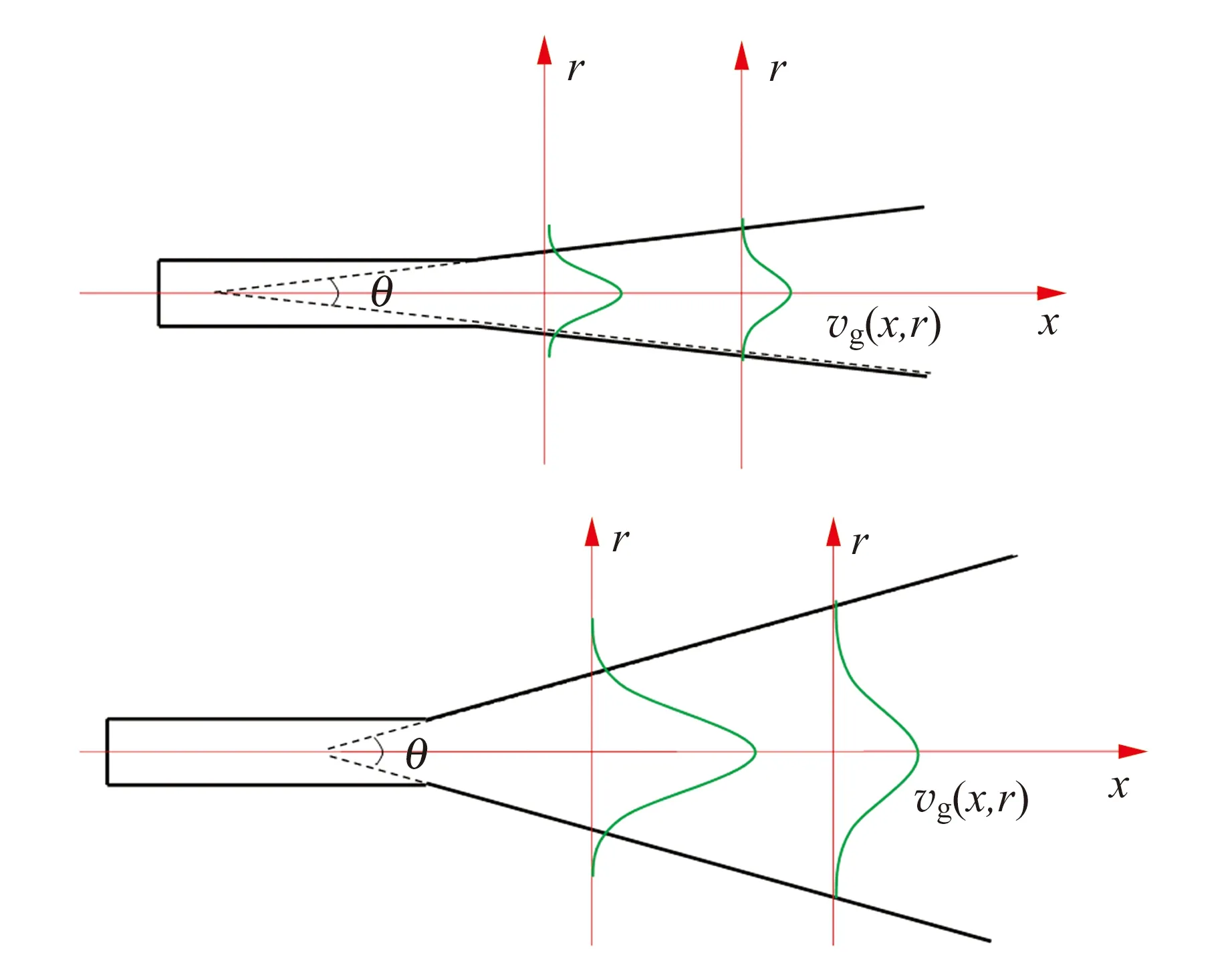
图7 不同流速时的张角
取氮气作为气源,不断增加气体的流速,并且测量气体在不同流速时的张角大小,发现正如推测的那样,存在流体状态的转变[15]. 当气体流速小于33 m/s时,θ的值较小,且在小范围内波动,使用平行于x轴的直线对数据进行拟合,得到此时射流的张角θ=0.76°;当气流速度大于50 m/s时,射流角度不再增加,同样拟合得射流的张角θ=22.92°;而对于速度在33~50 m/s之间的气流,可以认为气流处于由层流向湍流转化的过渡流状态,此时近似认为θ为vg的线性函数,即
θ=1.303 5vg-42.255
.
(9)
图8反映张角θ随着流速的变化,可以看出对应于流体的3种状态分别为层流、湍流和过渡流. 从数据拟合的结果来看,过渡流时取得的数据点接近直线的变化趋势,可见过渡流时确实符合这一变化趋势.
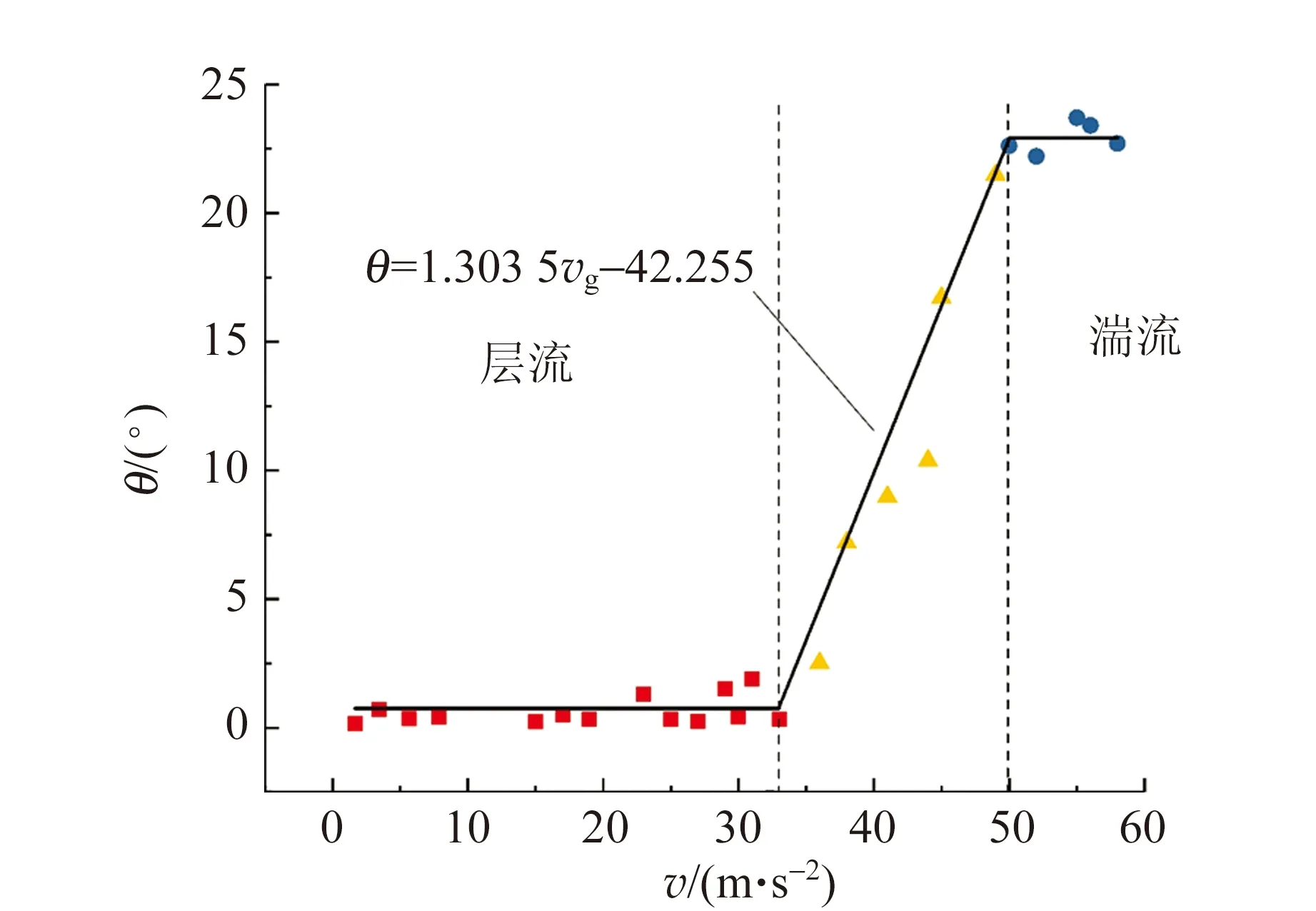
图8 射流与张角θ的关系
通过对以上结论的分析得知,影响阈值大小的因素是多方面的,接下来对3种不同的情况进行了研究.
层流情况:层流时,开口角度为0.76°,在本实验中气体速度低于33 m/s. 在泡泡膜形成处射流半径可写作R(x)=R0+xtan (0.76°/2) ,带入式(8),可得阈值的表达式为
(10)
湍流情况:湍流时,开口角度为22.92°,在本实验中气体速度大于50 m/s. 在泡泡膜形成处的射流半径可写作R(x)=R0+xtan (22.92°/2) , 带入式(8),可得阈值的表达式为
(11)
过渡流情况:过渡流时,开口角度在0.76°~22.92°之间,在本实验中将气体速度控制在33~50 m/s之间. 在泡泡膜形成处的射流半径可写作R(x)=R0+xtan [(1.303 5vg-42.255)/2],带入式(8),可得阈值的表达式为
(12)
针对喷嘴远离泡泡环时为什么会有3个速度值的问题,做进一步实验,所观察到的实验现象如图9所示.

图9 实验现象
通过对图9所观察到的实验现象分析得知,泡泡的形成比较复杂的实验过程. 当泡泡环与喷嘴有一定距离时,假如气流的速度小于v1时,不会形成泡泡,v1是第一个速度的阈值;当继续加大气流的流速,将吹出很多小泡泡,如果进一步增大流速时,突然发现泡泡不再形成,膜又变成了一个“深坑”,但是这个“深坑”与之前的有所不一样,这个深坑比当速度小于v1时形成的坑大得多,而不行成泡泡的最小值正好符合第3种情况时的阈值v3;当进一步增大流速,可以发现到某一值之后,又可以吹出泡泡了,只不过此时吹出的泡泡比之前的都要大很多,此时对应的能吹出泡泡的阈值和湍流情况时预测的阈值v2相对应.
至此,发现了一个奇妙的情况,对于吹泡泡,当喷口与泡泡环有一定距离后其实有3个阈值,而其中2个阈值分别对应于2种大小的泡泡. 将3个速度的阈值函数画出图像,如图10所示.
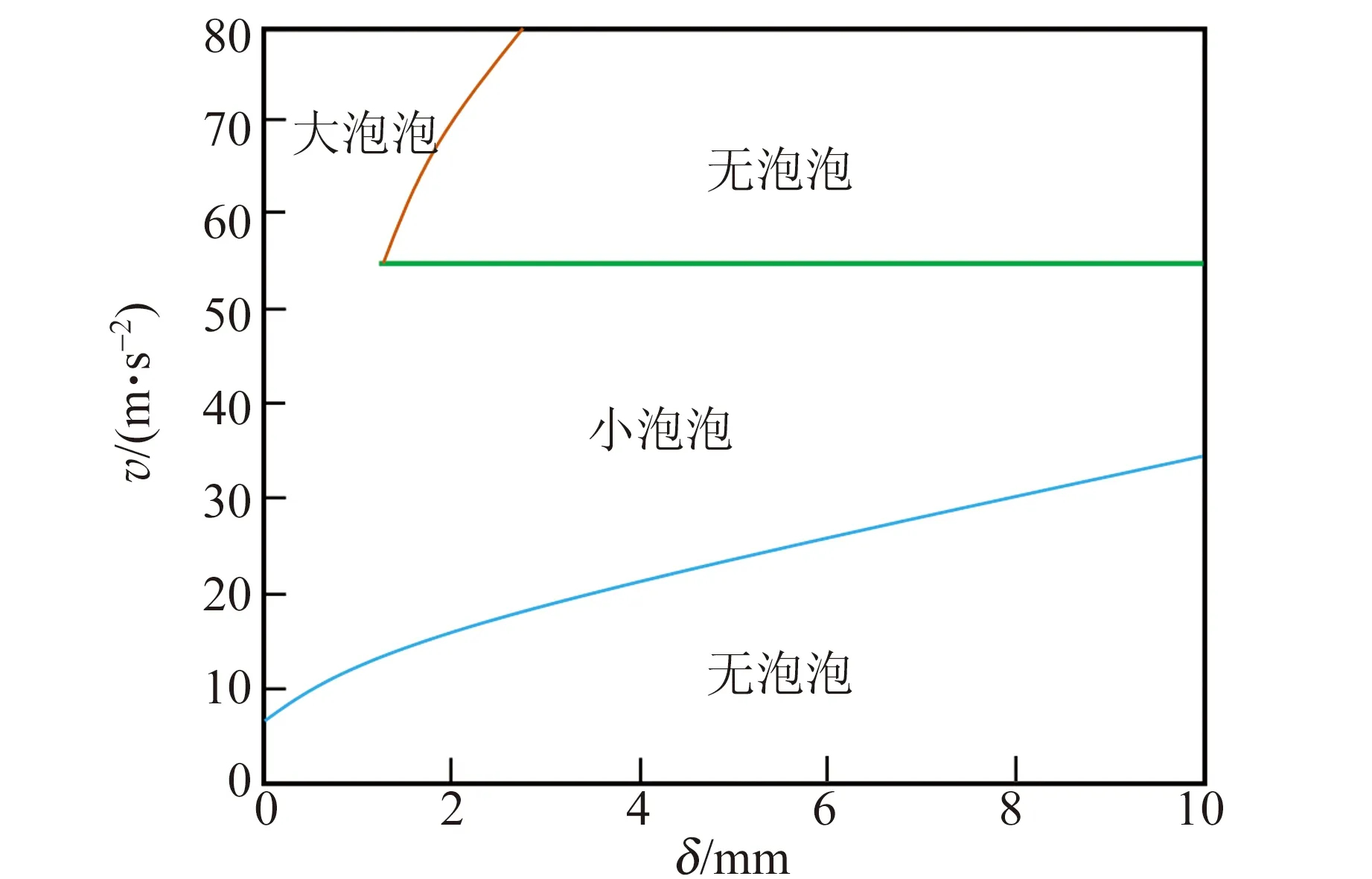
图10 能产生不同泡泡的区域
3 结 论
通过理论分析和实验验证可知,肥皂泡的形成是气体射流的惯性力与肥皂膜表面张力之间的竞争,并且气体射流在外界环境中的空气动力学形态对肥皂泡的产生具有显着影响. 当喷嘴与肥皂膜间距离较大时,让肥皂泡产生的气体速度范围有2个,小气泡会产生在小的气体流速范围(v1,v3)内,当气体流速高于v2时会产生大气泡. 小气泡速度阈值v1与雷诺数较低的层流气体射流相关,大气泡速度阈值v2与雷诺数较大的湍流气体射流相关. 从层流到湍流过渡的速度范围不会产生气泡. 当喷嘴与膜间的距离很小(在实验中小于0.9 mm)时,气体流动类型对气泡生成过程的影响很小,并且一旦气体速度高于最小的阈值v1时就会产生气泡.

