电液伺服振动试验台控制策略研究

高杨 巩明德 赵保强 干伟灿

（1.东风商用车技术中心，武汉430056；2.燕山大学，秦皇岛 066044；3.北京经纬恒润科技有限公司，北京 100191）

主题词：振动台 三状态控制 PD控制 电液伺服控制

0 前言

振动试验台是用来模拟振动环境的试验装置[1-3]。振动试验台被广泛应用于车辆研发领域，是检测和提高车辆零部件性能的必要手段。电液伺服振动试验台是一种先进的振动环境模拟设备，它以液压缸的往复运动模拟车辆振动环境，主要优点是具有大推力、大位移和良好的低频性能，在车辆及零部件试验场合中具有重要地位[4]。但同时电液伺服振动试验台存在控制难点，如频带宽度窄、容易失稳等，若仅采用位移反馈控制，很难实现较大的频带宽度和响应速度。

本文以电液伺服振动试验台为研究对象，建立单作动器阀控单作用液压缸的数学模型，设计了PD控制器和同时引入位移、速度、加速度3种反馈变量的三状态控制器。三状态控制器不仅能拓展系统频宽，同时改善了电液伺服系统动态特性，使电液伺服振动试验台的综合性能得到提升。

1 单作动器阀控单作用液压缸的数学建模

本文采用单活塞杆液压缸作为试验台执行机构，如图1所示为液压缸控制原理图。

图1 液压缸控制原理

图2为试验台液压缸电液伺服控制框图，输入信号由主控计算机产生，经控制器处理后进入伺服系统，经伺服放大器处理后，进入电液伺服阀并输出阀芯位移，最后控制液压缸的伸缩。系统中位移传感器用于采集液压缸的位置信息并反馈给控制器，构成位置反馈闭环系统。

图2 液压缸电液伺服控制过程

伺服放大器将微弱的电信号放大处理后驱动电液伺服阀工作[5]。伺服放大器的传递函数如式（1）。

式中：I(s)为输出电流信号拉氏变换；U(s)为输入电压信号拉氏变换；ka为伺服放大器增益。

电液伺服阀是电液伺服系统核心元件，能将电气信号转换为液压信号[6]。本文选用两级电液伺服阀，前置级采用双喷嘴挡板阀，输出级为滑阀。两级电液伺服阀传递函数常用二阶振荡环节表示，见式（2）。式中：X(s)为电磁阀芯位移信号拉氏变换；km为流量增益；ωm为固有频率；ξm为阻尼比。

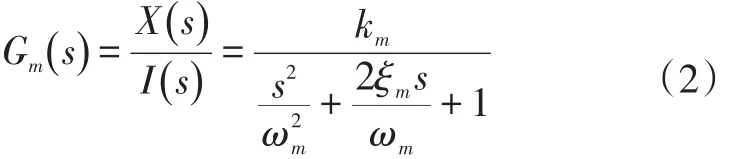
试验台采用非对称液压缸，图3为试验台阀控液压缸原理图。图3中，A1、A2分别为液压缸无杆腔及有杆腔有效截面积，P1、P2分别为无杆腔和有杆腔内的油液压力，PL为负载等效压力，Ps为液压源供油压力，PR为系统回油压力，Q1、Q2为经节流口流入和流出液压缸的流量，x为电磁阀芯位移，y为液压缸活塞位移。

图3 阀控液压缸原理

液压缸线性化流量方程见式（3）。

式中：QL为负载流量；kqf为静态流量增益；x为阀芯位移；PL为负载压力；kcf为流量-压力系数。

负载流量连续性方程见式（4）。

式中：Cte为液压缸等效泄漏系数；Vt为液压缸两个腔室的总容积；βe为体积有效弹性模数；A为活塞有效面积；y为活塞位移。

忽略库仑摩擦及油液质量，可得液压缸负载力平衡方程式（5）。

式中：mt为外负载质量与活塞杆折算到活塞上的质量之和；Bt为油液粘性阻尼系数；kt为负载的弹性刚度；FL为施加在活塞上的负载力。

进行拉氏变换，整理并化简得式（6）。

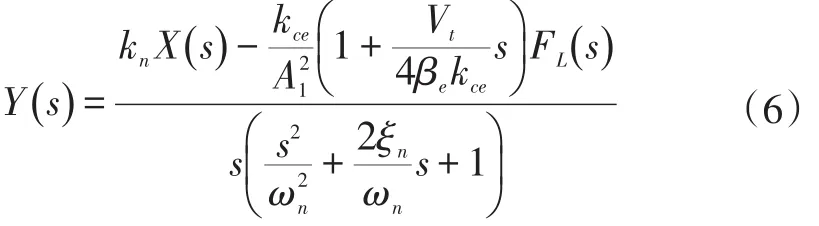
式中：kn为液压缸等效开环增益；kce为总的流量-压力系数；ωn为液压固有频率；ξn为液压阻尼比。

由式（6）得液压缸活塞杆位移对伺服阀位移的传递函数（7）。

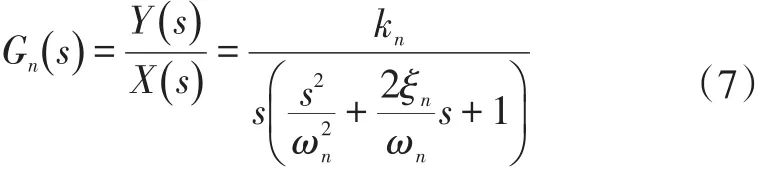
由式（6）得液压缸活塞杆位移对外负载力的传递函数为式（8）。

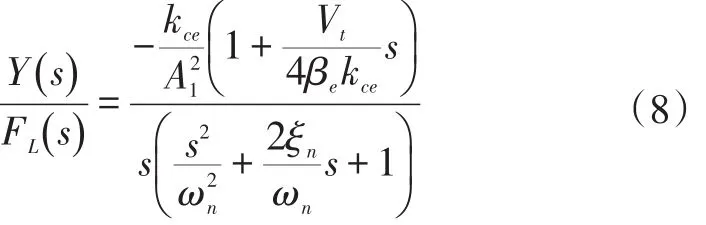
通过前文分析得到的电液伺服系统传递函数结构图见图4。

图4 电液伺服系统传递函数结构

系统开环传递函数为式（9）。

表1给出了电液伺服系统的主要参数。

表1 电液伺服系统主要参数

图5为闭环系统的零极点分布图，所有极点均位于虚轴的负半轴，可见系统是稳定的。图6是闭环系统的单位阶跃响应，系统调节时间较长，需要增加校正环节以满足系统动态性能需求。

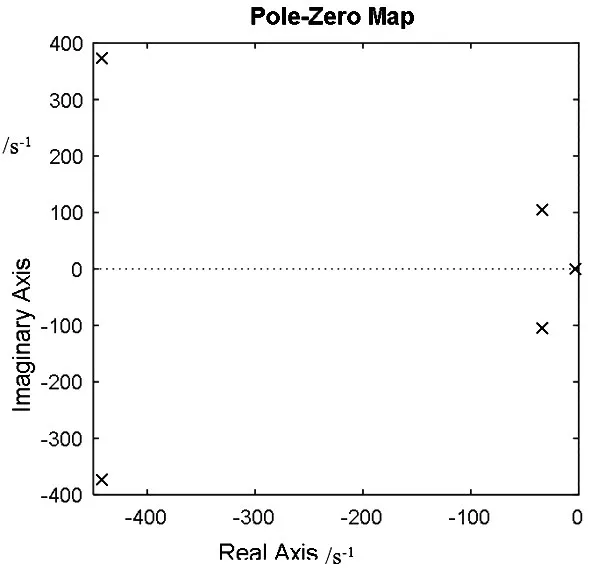
图5 闭环系统零极点分布

图6 闭环系统单位阶跃响应

2 电液伺服系统控制器设计

2.1 PD控制器设计

在工程中PID控制器的应用最为广泛，由于积分环节易导致电液控制系统发生超调和震荡，本文不引入积分（I）控制器，而采用PD控制器[7]。PD控制器的传递函数如式（10）。

式中：Kp为比例增益；Kd为微分增益，Kd=KpTd。

加入PD控制器进行系统校正，系统的控制框图如图7所示。

图7 PD控制系统

图中，Kp和Kd为PD控制器参数，Gk(s)为系统开环传递函数。

PD控制器参数采用Ziegler-Nichols（Z-N）参数整定方法确定[8]。其中，比例增益Kp=6.756 2，微分增益Kd=0.149 1。利用PD控制器对系统校正，并通过单位阶跃响应和闭环Bode图检验系统校正效果[9]。校正后系统的单位阶跃响应曲线如图8所示，系统的动态调整时间减少，满足快速性要求。校正后系统的闭环Bode图如图9所示，系统的频宽达到126 rad/s（大约20 Hz），对于本系统30 Hz的频宽要求还未达到。

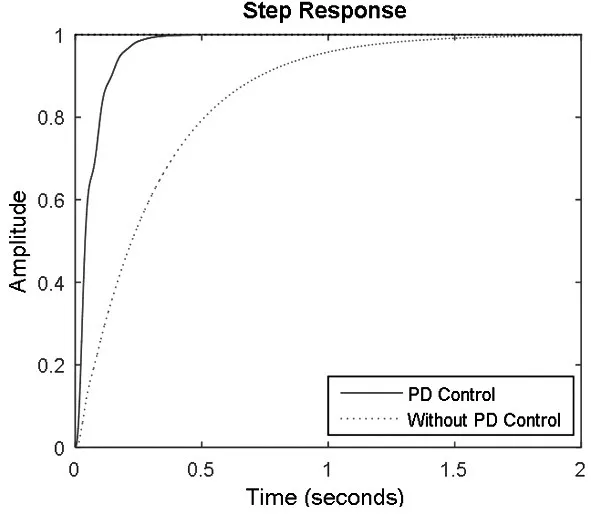
图8 PD控制系统单位阶跃响应

图9 PD控制系统闭环Bode图

本节设计的PD控制器可以满足低频运动系统的控制要求，但难以满足较高频率系统对频带宽度和稳定性的控制要求，需要考虑其他控制策略。

2.2 三状态控制器设计

三状态控制是在电液伺服系统中引入位置、速度和加速度三状态控制。本文利用三状态控制，通过状态反馈逆规划期望极点，得到期望的系统性能。

2.2.1 三状态反馈控制

应用极点配置方法配置系统极点，三状态反馈控制系统的闭环传递函数为式（11）。

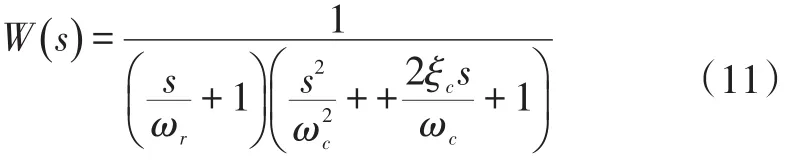
式中：ωr为期望系统最终频宽对应的频率；ωc为1.05～1.20倍的液压固有频率；ξc取值为0.7。

根据上文建立的电液伺服控制系统数学模型，得到简化后的系统开环传递函数为式（12）。

图10所示为三状态反馈控制框图，kdf、kvf和kaf为三状态反馈控制参数。

图10 三状态反馈控制系统

三状态反馈控制系统的闭环传递函数为式（13）。

为得到三状态反馈的三个待求解参数，令三状态反馈系统传递函数与期望的传递函数相同，即令

综合式（11）、（13）得三状态反馈参数为：

2.2.2 三状态顺馈控制

三状态顺馈控制在三状态反馈控制的基础上，对消闭环传递函数距虚轴较近的主导极点，达到拓展系统频宽的目的[10,11]。

三状态顺馈控制器的传递函数如下式，kdr、kvr和kar均为待定系数。

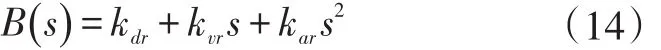
B(s)需要对消ωc的振荡环节，即三状态顺馈控制器应满足：

联立式（14）、（15）代入数据后得：

完整的三状态控制系统框图见图11所示。

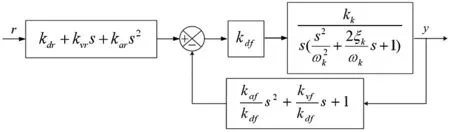
图11 三状态控制系统

由图11和式（15）得到系统闭环传递函数见式（16）。

将ωr=185 rad/s代入上式得：

三状态控制系统Bode图如图12所示，系统频带宽度达到185 rad/s（约为30 Hz），可见三状态控制器能够有效拓展系统频宽。

图12 三状态控制系统Bode图

3 电液伺服控制系统仿真分析

3.1 PD控制器与三状态控制器仿真对比

为进一步验证两控制器的控制效果，建立电液伺服控制系统的Simulink仿真模型，选取阶跃信号和正弦信号作为模型输入信号进行动态仿真分析。如图13所示为电液伺服控制系统的Simulink仿真模型。

当输入信号为目标幅值0.1 m的阶跃信号时，两控制器的阶跃响应曲线对比如图14所示，三状态控制器的调整时间和最大超调量均小于PD控制器，这表明三状态控制器的动态特性满足快速性和平稳性的要求，对扰动的适应性优于PD控制器。

当输入频率为1 Hz的正弦信号时，两种控制器的响应曲线如图15所示。三状态控制器响应信号跟随输入信号的效果很好，基本不受负载干扰力的影响，PD控制系统输出信号基本可以跟随目标信号，但受负载干扰的影响较大。

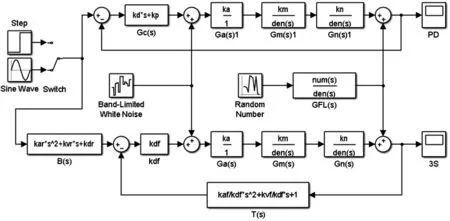
图13 电液伺服控制系统Simulink仿真模型

图14 两种控制器的阶跃响应曲线对比

图15 目标信号为1 Hz正弦信号的响应曲线对比

如图16所示，当目标信号为10 Hz正弦信号时，PD控制器已不能满足控制要求，而三状态控制系统输出信号仍能很好的跟随目标信号。

图16 目标信号为10 Hz正弦信号的响应曲线对比

3.2 三状态控制仿真分析

选取幅值分别为5 mm和10 mm，频率分别为1 Hz、5 Hz和10 Hz的正弦信号作为目标信号进行三状态控制仿真分析。

如图17所示，当目标信号为较低频率的正弦信号时，三状态控制器复现目标信号的效果显著。当目标信号频率增大时，三状态控制器复现目标信号的效果较好，虽相位稍有滞后，但控制精度仍能满足工程需要。当目标信号频率相同时，以幅值10 mm与幅值5 mm的正弦信号为目标信号的复现效果无显著差别。可见在一定的幅值范围内，三状态控制效果受目标信号的频率影响较大。

图17 三状态控制仿真曲线对比分析

综上所述，本文设计的三状态控制器可以有效地提高系统的动态特性，获得良好的系统性能指标。

4 结论

本文以电液伺服振动试验台为研究对象，研究振动控制策略的关键技术。完成单作动器阀控单作用液压缸的数学建模，设计了PD控制器和三状态控制器。建立了电液伺服系统传递函数，结合系统主要参数，分析系统的动态特性。针对PD控制器难以满足系统频宽的问题，设计基于极点配置的三状态控制器以拓展系统频带宽度，Simulink仿真验证了三状态控制策略的可行性。仿真结果表明，三状态控制器能有效拓展系统频宽，改善系统动态特性，对阶跃信号和正弦信号的复现效果较PD控制器更佳。加强对振动试验台三状态控制的研究，有助于提高试验台的动态性能，满足更多试验需求。