基于Flow-3D的多阶明渠工程数学模型研究

李大鸣，贾明灏，张弘强，李彦卿，孙仲谋，栗琪程,熊继斌

(1 天津大学 水利工程仿真与安全国家重点实验室，天津 300350;2 德州市水利勘察设计研究院，山东 德州 253014)

灌区渠道作为水工建筑物及农田水利中的重要输水工程之一[1]，其设计方案的合理性必须得到保证。但由于投资成本、试验周期等因素的影响，小型灌渠工程在设计过程中一般仅采用单纯的水力计算，而鲜有进行物理模型试验的条件。Thom等[2]最早采用手算方法得到了不可压缩黏性流体绕圆柱流动的差分数值解，之后数值研究方法在三维流体运动中的应用逐渐展开。随着数值模拟技术的发展，通过应用相关流体计算方法及商业软件，便可验证工程设计方案的可行性及合理性[3]。

Leendertse等[4]在三维浅水方程基础上，用固定分层法将计算水域在垂直方向上划分为多个水层，通过沿水深方向对每层积分，将三维问题转换为多个二维问题并对其离散求解，简化了求解三维流体运动问题的难度。赵士清[5]、周思平等[6]采用类似方法分别分析了长江口潮流运动、自由表面处理方法。吴修广等[7]采用三维坐标转换建立了弯曲河道的计算模型。张光碧等[8]采用VOF模型对不规则边界河道水流流场进行了模拟。张大伟等[9]采用Godunov格式的有限体积法，建立了复杂明渠水流运动的高适用性数学模型。于鹏[10]以东汶河治理工程为例，研究了二维水流数学模型在水面线推求中的应用。刘英等[11]研究了不同因素对渠道水力特性的影响。陆虹等[12]研究了引水明渠的水力学特征对设计渠道断面型式及控制渠道泥沙淤积的影响。杨程等[13]采用SIMPLEC算法求解紊流方程，建立了基于非结构网格的三维水流数学模型。在河渠水沙研究方面，黄永健等[14]、王景元等[15]结合灌区的结构特点及水流泥沙特性，建立了黄河下游灌渠水流泥沙数学模型。陈绪坚等[16]提出了保持冲积河流稳定的最小可用能耗率原理与公式。Dou等[17]从黄河水沙输运过程的角度进行了水沙数值模拟。以上研究虽从不同方面分析了河渠工程的水力特性及泥沙淤积问题，但对灌区多阶明渠的水力特性及泥沙淤积尚鲜有涉及。为此，本研究通过建立山东省德州市牛角店输水工程的整体三维数学模型，基于VOF方法，在Flow-3D平台上研究多阶明渠工程在不同工况下的水面线变化、流速分布及泥沙淤积情况等，分析对比不同工况下渠道各级阶梯的水力特性，验证了工程设计方案的合理性，并分析其对工程项目的影响，以期为灌区多阶明渠的水力特性及泥沙淤积研究奠定基础。

1 材料与方法

1.1 模型理论

1.1.1 基本控制方程 三维非恒定不可压缩流体的基本控制方程如下。

连续性方程：

(1)

运动方程：

(2)

式中：x、y、z为空间坐标分量；u、v、w分别为x、y、z方向的速度分量；t为时间；ρ为密度；p为压强；ν为流体运动黏性系数；fx、fy、fz分别为x、y、z方向的质量力分量。

1.1.2 紊流k-ε方程 渠道水流的运动形式多呈紊流形式，而在紊流中流体的连续介质假定仍成立，流体运动的基本方程仍然适用。为了描述紊流的时均性质，对方程(1)和(2)进行时间平均，得到雷诺平均应力方程,再将其与描述紊流性质的方程组成封闭系统，便可构成紊流模型。

绝大多数紊流模型均立足于Boussinesq[18]关于紊动黏性系数νt的假设：

(3)

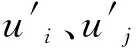
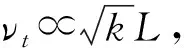
(4)

式中：Cμ为经验常数。k和ε可分别用k方程和ε方程描述其在空间的分布规律及随时间的演化规律，这两个方程可由N-S方程导出。

k方程：

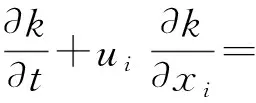
(5)

ε方程：

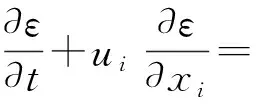
(6)

式中：σk、σε、Cε1、Cε2为经验常数。

根据Launder等[21]和Rodi[22]对k-ε紊流模型的讨论及紊流经验常数的研究，Cμ、Cε1、Cε2、σk、σε的值可按表1选取。

1.1.3 泥沙沉速公式 工程位于黄河下游灌渠中，悬移质是输沙的主体，若不考虑推移质影响，可用悬移质输沙率公式近似作为水流挟沙力公式。应用Flow-3D泥沙冲刷模块，参考山东省水利科学研究院推荐的引黄衬砌渠道远距离挟沙公式[23]，有：

(7)

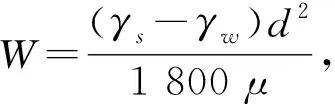
表1 k-ε紊流模型经验常数表Table 1 Empirical constants of k-ε turbulent model

1.2 模型建立

1.2.1 工程概况 牛角店输水工程地处山东省德州市临邑县牛角店村附近，位于引徒总干渠和李家岸干渠之间,如图1所示，是连接两干渠的重要输水工程。其中，李家岸干渠是李家岸引黄灌区的灌渠工程，李家岸引黄灌区是全国大型引黄灌区之一。工程位置处李家岸干渠底高程为16.43 m，引徒总干渠底高程为12.00 m。

图1 牛角店输水工程位置示意图Fig.1 Location of water conveyance project in Niujiaodian

渠道最大输水流量80.00 m3/s，上游最高水位为19.63 m，下游最高水位为15.50 m，水面差为4.13 m。渠道设计长度为83.25 m，宽度为16.00 m。渠道上首采用光滑坡面连接干渠与渠道，渠道整体横断面采用U型断面，底部呈三级阶梯状，阶梯末端设置为挑坎跌流形式，渠道纵剖面如图2所示。

1.2.2 三维建模 依据牛角店输水工程初步设计图建立三维实体参数模型作为模拟对象。考虑工程设计中对模型参数的修改及模型调试的便利，使用Revit进行参数化分族建模[24]，由于模型上游坡面形式复杂，故需对其进行细部处理。

模型构建工作主要从工程结构特点出发，将牛角店输水工程总体模型分为侧墙、底槽、护坡3部分；同时根据沿程结构形式的不同，将模型分为6段分别进行参数化建模，结果见图3。

图2 渠道纵剖面图(单位：mm)Fig.2 Longitudinal section of channel(Uint:mm)

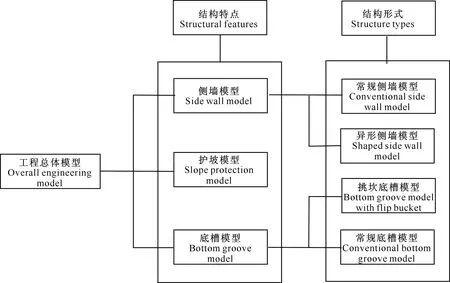
图3 牛角店输水工程三维实体参数模型分块示意图Fig.3 Blocks of three-dimensional solid parameter model for water conveyance project in Niujiaodian

对于结构形式简单的常规模型采用拉伸、放样等方式进行建模；对于结构形式有变化和结构形式复杂的分段，如进水口坡面、出口扩散段等，采用放样融合与布尔运算等手段进行建模。将建立的各部分模型进行拼装，即得到牛角店输水工程三维几何模型,如图4所示。

图4 牛角店输水工程三维几何模型Fig.4 Three-dimensional model of water conveyance project in Niujiaodian

1.2.3 网格划分 网格剖分是数值模拟的第一步，网格划分的质量直接影响计算结果的稳定性与计算精度[25]。在实际处理水体流动问题时，常根据计算域的自然边界和地形条件选取合适的网格划分方法及网格尺寸，以保证网格质量满足计算要求。

由于牛角店输水工程模型结构形式相对规则，采用结构化网格既能满足模型要求，又能减少计算的复杂程度。几何模型采用1∶1的实体参数模型，因此模型整体计算域较大，根据实际模拟需求及模拟条件，选用0.30 m的立方体结构化网格，划分网格总数为1 098 981个。同时，对于上游坡面和下游坡面等复杂结构形式，采用局部加密的方法，用0.15 m的网格对其加密，加密网格数为367 360个。

1.2.4 边界条件及参数设置 牛角店输水工程模型范围上起李家岸引黄总干渠护坡处，下至引徒总干渠护坡处，模型包括的边界条件有上游边界水位、下游边界水位、上游来流速度、下游初始水位及网格划分后各网格的边界。

上游边界(Y方向)水位从最高至最低水位设置4种工况，分别为19.63，19.38，19.23和18.93 m；下游边界(Y方向)水位取定水位15.50 m；上游来水初始流取为0；下游初始水位取下游边界水位；顶边界(Z方向)取空气边界；底边界(Z方向)取不透水墙边界；上游左右边界(X方向)取对称水力边界；下游左右边界(X方向)取自由出流边界。

采用Flow-3D进行数值计算，选取空气夹带模块(air entrainment)、重力和非惯性参考系模块(gravity and non-inertial reference frame)、黏度和湍流模块(viscosity and turbulence)、沉积物冲刷模块(sediment scour)及密度评估模块(density evaluation)5个物理模块。湍流模型选择标准k-ε模型，表面张力系数取0.073，重力加速度取-9.81 m/s2。糙率选择按人工渠道糙率值选取，由于渠道表面为不抹光的水泥表面，故选取糙率值为0.014。

选取20 ℃的水作为计算流体，模型沙参考黄河下游灌区相关水文泥沙数据[26-27]，取泥沙密度为2 650 kg/m3，其中值粒径为0.013 mm，含沙量为8.9 kg/m3。工况设置按表2所示分为8种。

表2 计算工况设置Table 2 Settings of calculation cases

2 结果与分析

初始渠道内无水体流动，模拟完成从上游来水到流态稳定后的渠道内水流情况。模拟结果显示，在计算时间达到42～68 s时，各工况水流流态渐趋稳定，为保证不同工况的水流均达到稳态，选取200 s时的计算数据作为代表数据。

2.1 流速分布及变化情况

2.1.1 清水流速分布及变化情况 在不考虑水流挟沙情况下，研究清水水流沿程流速分布及变化情况，分析其对牛角店输水工程产生的影响。为便于不同工况的对比分析，选取渠道中轴线(X方向)处的水流纵剖面，研究不同水位工况下流速分布及变化情况，得到渠道中轴线处不同水位的流速分布及水面线如图5所示。根据图5结果可知，在渠道水流进入稳态后，第一级阶梯与第三级阶梯后半段整体流速比较平稳。由于阶梯挑坎的存在，在挑坎及挑射水流下落处水流流速较大，流态不平稳。同时，由于阶梯上水层较薄、阻水效果不明显及挑流效应的影响，最大流速出现在第二级阶梯上挑流水舌末端处。在第三级阶梯，由于下游初始水位的存在，其对挑射水流有较明显的阻力作用，水流挑射效果不明显，在水舌下落位置后方，由于回流作用形成漩涡，故在第三级阶梯前端出现负速度。

在不同工况下，水流的整体流速略有不同，随着上游边界水位的降低，渠道内整体流速逐渐减小，从图5(a)、(d)可以发现，由于上游水深从3.20 m降至2.50 m，第一级阶梯水流整体流速从2.40 m/s降至约1.30 m/s。通过对比图5 (a)～(c)可以发现，随着水位的降低，最大流速也从7.50 m/s降至5.64 m/s。图5(d)表明，随着水位降低，挑流消能效果也越差，导致第二级阶梯上的水流最大流速较大。

通过以上分析、对比发现，渠道整体水流流速分布比较平稳，但是在挑坎处由于边界条件的改变，流场急速变化，在施工及维护过程中应该考虑提高挑坎的混凝土强度等级。同时，由于挑流效应的影响，第二级阶梯上流速较大，对渠道底板混凝土冲刷作用比较明显，挑流水舌后也容易出现水流与混凝土边界分离，容易产生空蚀现象。

2.1.2 挟沙水流流速分布及变化情况 对于挟沙水流，其剖面选择等均与清水条件下相同，图6为渠道中轴线处不同水位的流速分布及水面线图。图6结果表明，挟沙水流进入稳态后，第一级阶梯与第三级阶梯后半段水流流态整体比较平稳。第二级阶梯与第三级阶梯前半段由于挑坎存在，水流流态急速变化。同时，由于泥沙淤积第二级阶梯水层变薄，消能效果减弱，水流流速整体偏大；第三级阶梯上依然有较明显的漩涡存在。

在不同工况下，随着水深降低，挟沙水流整体流速逐渐降低。根据图6(a)～(d)的计算结果，水流在第一级阶梯的整体流速从2.60 m/s下降至1.50 m/s左右。图6(a)～(c)表明，随着水位降低，泥沙沉降量逐渐增加，第二级阶梯渠底水力条件发生变化，同时由于第一级挑坎后水舌与混凝土壁面间形成负压区，相对加大了作用水头，最大流速逐渐增大，从7.60 m/s增至9.30 m/s。从图6(d)可以看出，当水位降至一定高程时，第一级挑坎挑射水流出现与混凝土边壁分离的情况，挑流水舌与空气掺混，消能效果提升，最大流速较小。

通过上述分析、对比发现，第二级阶梯上流速偏大，对混凝土底板的冲刷作用明显，需要加强防护。同时，当水位降至一定程度时，出现挑流水舌与混凝土边壁分离的情况，需要防止混凝土空蚀破坏。

2.1.3 流速对比分析 通过上述2.1.1和2.1.2节的分析，不同水位工况下水流的速度分布及变化情况基本符合水流的实际变化规律。根据以上计算结果，得到明渠最大流速及渠道出口断面平均流速如表3所示。

表3 各工况下渠道内典型流速Table 3 Typical flow velocity in the channel under various cases

对比图5和图6及表3各对应工况下的水流流速状况可以发现，挟沙水流的整体流速略大于清水水流的整体流速。清水条件下，随水位降低，水流最大速度逐渐减小；而对于挟沙水流，由于泥沙沉积与冲刷，渠底水力边界发生改变，水流最大流速规律相应改变。根据表3计算结果，除工况8外，挟沙水流出口断面平均流速较清水大0.50～0.86 m/s。同时，挟沙水流渠道内最大流速也大于清水条件。参考钱宁等[28]《泥沙运动力学》中的相关试验结果，挟沙水流在一定程度上减少了水流的紊动程度，降低了水流能量耗散，水流动能增大，相应水流流速增大，说明模型计算结果与实际试验效果相符。

2.1.4 渠道正剖面流速分布及变化情况 上述2.1.1～2.1.3节分析了不同水位工况下水流沿程的速度分布及变化情况，作为影响渠道安全的重要因素，渠道中水流流速沿高度方向的变化也需要加以重视。为便于分析渠道正剖面的流速情况，按照挟沙水流的计算条件，取工况2下的水流作为分析对象，剖面选取各级阶梯中水流流态较稳定位置作为分析断面。图7即为渠道各级阶梯正剖面流速分布图。

图7结果表明，挟沙水流进入稳态后，第一级阶梯与第三级阶梯中水流流态整体比较平稳，流速分布均匀。由于第一级挑坎挑流作用，第二级阶梯上水流流速分布不均匀。同时由于泥沙淤积，第二级阶梯水层变薄，消能效果减弱，水流流速整体偏大。第三级阶梯上水流由于处于接近淹没出流的水力条件，水流流速较第二级阶梯有所减小。

根据图7(a)的计算结果，水流在第一级阶梯上流速分布均匀，中间最大流速为2.79 m/s，越接近渠道两侧及渠底，水流流速越小。图7(b)所示截面位于第二级阶梯中部，水流流态最不稳定，流速分布较为不均，最大流速为8.54 m/s，出现在渠道水流靠中心左侧上表面位置。图7(c)所示截面为第三级阶梯中部，由于第二级挑坎的挑流作用，水流上表面因消能作用流速减小，最大流速4.14 m/s出现在水体中部，同时第三级阶梯下部水体的流速普遍大于上部水体的流速。

通过上述分析发现，第二级阶梯上流速偏大且水层较薄，弱化了水体对混凝土渠底的保护作用，挟沙水流对混凝土底板的冲刷作用明显，需要采取保护措施或适当提高渠底混凝土强度等级。

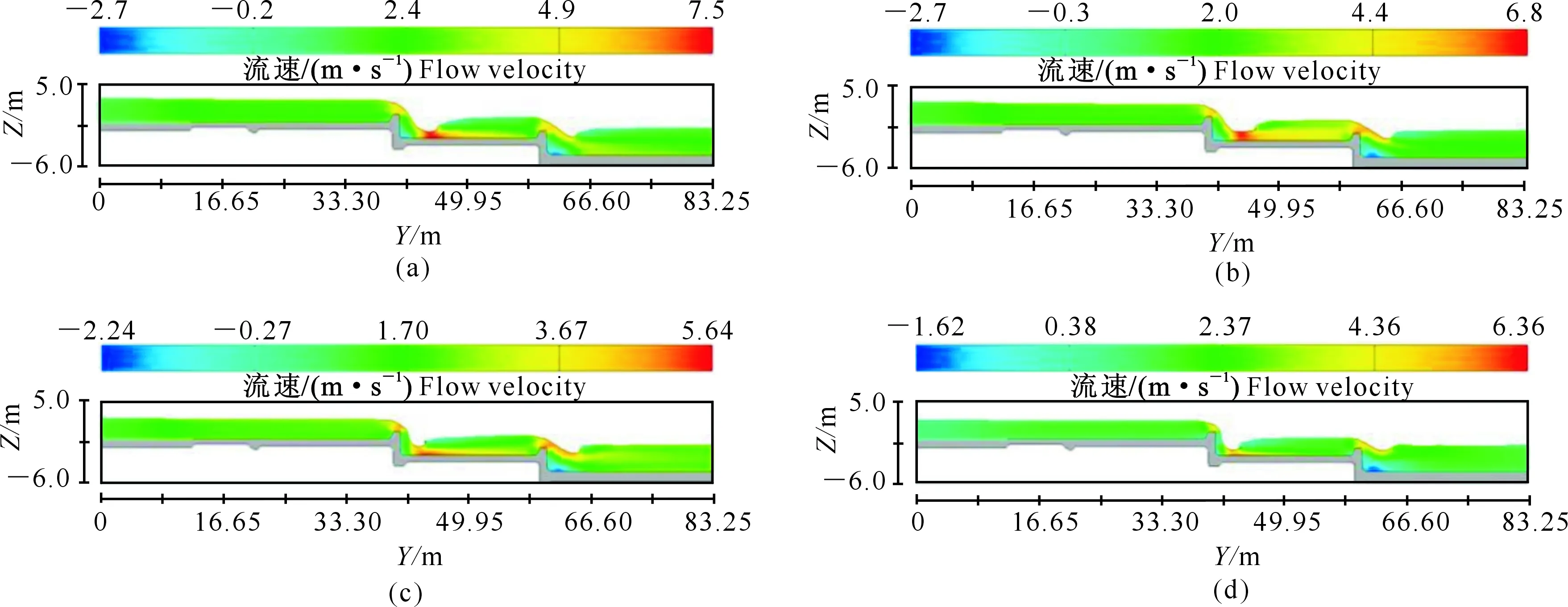
(a)工况1；(b)工况3；(c)工况5；(d)工况7(a) Case 1;(b)Case 3;(c)Case 5;(d)Case 7图5 清水条件下渠道纵剖面水流流速及水面线Fig.5 Flow velocity and water surface line of channel longitudinal section under clear water conditions

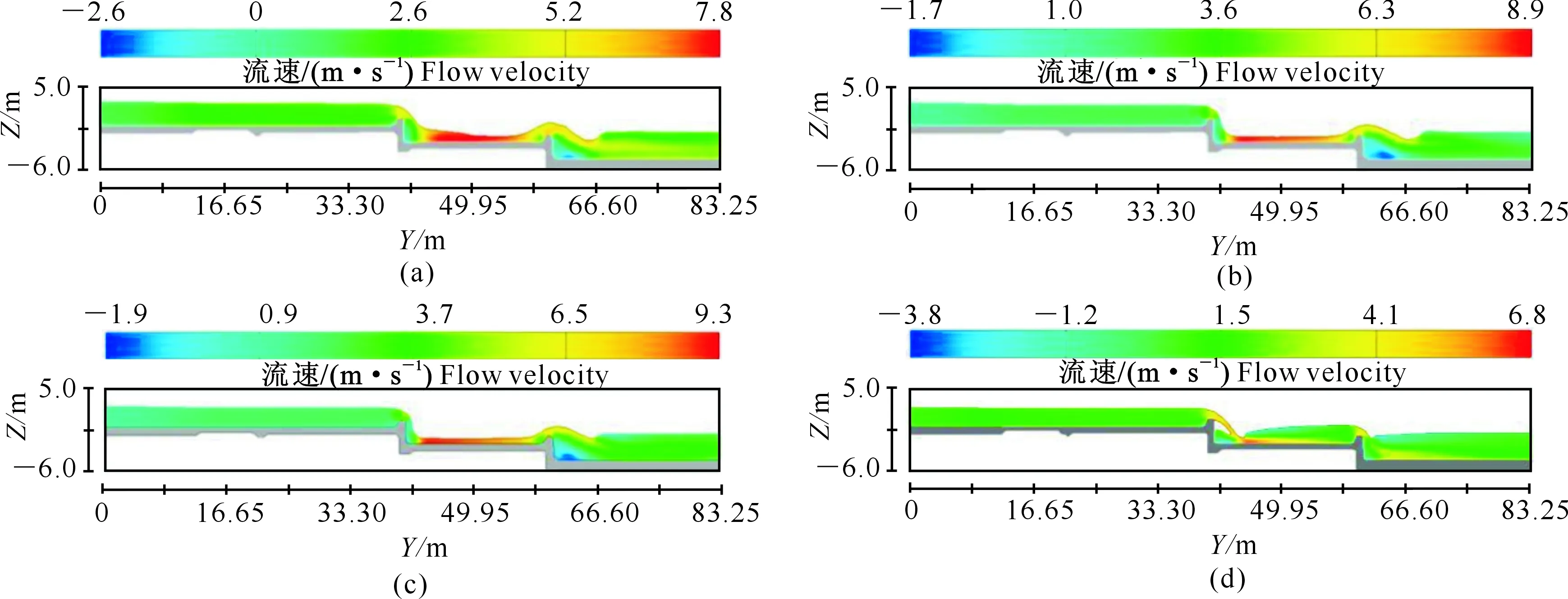
(a)工况2；(b)工况4；(c)工况6；(d)工况8 (a)Case 2;(b)Case 4;(c)Case 6;(d)Case 8图6 挟沙条件下渠道纵剖面水流流速及水面线Fig.6 Flow velocity and water surface line of channel longitudinal section under sediment carrying conditions

图7 挟沙条件下渠道正剖面水流流速Fig.7 Flow velocity of channel positive section under sediment carrying conditions

2.2 水面线变化

2.2.1 清水条件下水面线的变化 对比图5(a)～(d) 4种工况，由于下游边界水位均为15.50 m，在水流流态稳定后，第三级阶梯水面线基本相同。随着上游水深的降低，第二级阶梯水面雍水线逐渐降低。根据工程施工图，第二级阶梯侧墙高度为19.00 m，在计算时间为6 s左右时，水流下泄至第一级挑坎，此时水流流态不平稳，部分水体会溢出侧墙，在施工过程中需要考虑适当增大侧墙高度，保证水流不溢出渠道。

2.2.2 挟沙水流水面线的变化 通过图6(a)～(c) 3种工况可知，第一级阶梯随上游水位降低水面线略有降低，第三级阶梯水面线与下游边界水位基本持平。第二级阶梯上水面线随水位降低而降低，其主要原因为水流流速增大、过水面积减小。对于图6(d)，由于挑流水舌与空气混掺，能量损失增大、流速变小、过水断面增大、水面线抬高。

2.2.3 水面线对比分析 根据模拟结果，得到各工况下典型位置处的水位如表4所示。

表4 各工况下渠道内典型位置的水位Table 4 Typical location water level in the channel under various cases

通过2.2.1和2.2.2节分析，可得到不同水位工况下的水面线情况。对比图5和图6及表4结果发现，相同水位下的水面线，由于挟沙水流流速略大，过水断面面积略有减小，水面线略有降低。第二级阶梯由于水流流速差异较大，挟沙水流水面线比清水条件有明显下降，但在第二级挑坎处由于泥沙淤积水面线有明显抬升。同时，从表4可以看出，清水条件下一级挑坎水位与边墙高度差最小时仅有0.39 m的高度差，二级挑坎水位与边墙高度差最小时仅有0.36 m；挟沙水流二级挑坎水位与边墙高度差最小时仅有0.30 m。当水流流态发生改变时，这些位置极易出现溢出问题，但由于下游初始水位较高，且第二级挑坎后出流条件接近淹没出流，较之第一级挑坎后出流条件平稳，故应重点关注第二级阶梯边墙。

2.3 泥沙淤积情况

2.3.1 渠道纵剖面泥沙淤积情况 泥沙沉降和淤积问题是明渠挟沙水流的重点关注问题之一，挟沙水流中泥沙沿程的沉积情况如图8所示。根据图8结果，在渠道水流进入稳态后，第一级阶梯上无明显的泥沙沉积，主要原因是选取的计算时间均为200 s，且水流在此阶段的流动情况也比较稳定，泥沙沉积效果并不明显。第二级阶梯前半段由于水流流速较大，薄水层阻水效果不明显，也未见明显的泥沙沉积，而第二级挑坎前由于挑坎的阻拦作用，有较明显的泥沙沉积。由于第三级阶梯有较高初始水位，水层较厚，阻水效果明显，水流挟沙能力减小，故泥沙沉积量较大。

当上游水深发生改变时，泥沙沉积量也随之发生变化，从图8(a)、(d)可以发现，上游水深从3.20 m降至2.50 m时，泥沙最大沉积厚度从0.134 mm增加至0.143 mm，说明随着水位降低，水流整体流速减小，水流挟沙能力降低。同时，对比4种工况，发现泥沙沉积量最多处位于第二级挑坎后方与挑流水舌之间，主要原因是挑流水舌后方存在漩涡、水流流态极其不稳。随着水流继续流动，泥沙沉积量有下降趋势。

通过上述分析、对比发现，泥沙易沉积在挑坎前及第三级阶梯上。为解决泥沙沉积问题，建议及时采取清淤措施、合理调整运行方式，控制挑坎前的泥沙沉积量。考虑下游初始水位较深时，泥沙易沉积，同时由于模拟时间仅计算至200 s，随着计算时间延长，泥沙淤积问题也会愈发严重，在工程实际运行过程中需要对下游水深进行控制，并且及时采取清淤措施。

2.3.2 渠道正剖面泥沙淤积情况 泥沙沉降和淤积主要考虑其沿程变化情况，正剖面图则给出渠道正断面中泥沙沿X方向的分布规律，挟沙水流中泥沙正剖面的沉积情况如图9所示，由于阶梯前泥沙的沉积规律相似，故以第二级阶梯前的正剖面泥沙淤积情况作为阶梯前泥沙淤积的代表。

根据图9计算结果，在渠道水流流态平稳后，第二级挑坎前由于挑坎的阻拦作用，有较明显的泥沙沉积。由于第三级阶梯有较高初始水位，水层较厚，阻水效果明显，水流挟沙能力减小，故泥沙沉积量较大。从图9(a)可以发现，泥沙淤积沿X方向分布较均匀，泥沙沉积量在0.130 mm左右，在靠近侧墙位置处有较明显变化，主要原因是侧墙位置处计算网格包含水体与墙边界两部分，墙边界的泥沙计算结果必为0，Flow-3D为保证计算结果的连续，在该处会采用插值形式使该位置处计算结果变为渐变形式。由于图9(b)的断面位于第三级阶梯出口扩散段位置，挟沙水流存在向两侧的扩散现象，泥沙沉降存在由渠道中心向两侧递减的规律，中心处泥沙最大沉积量为0.129 mm，向两侧逐渐减至0.001 mm。

通过上述分析发现，第二级阶梯挑坎前泥沙沉降均匀，第三级阶梯泥沙有明显沉降规律。需要及时采取清淤措施清除挑坎前沉积泥沙，同时可通过调控渠道水流流量冲刷第三级阶梯上的沉积泥沙。

(a)工况2；(b)工况4；(c)工况6；(d)工况8(a)Case 2;(b)Case 4;(c)Case 6;(d)Case 8图8 牛角店输水工程渠底泥沙沉积纵剖面图Fig.8 Longitudinal section of sediment deposition at the bottom of water conveyance channel in Niujiaodian

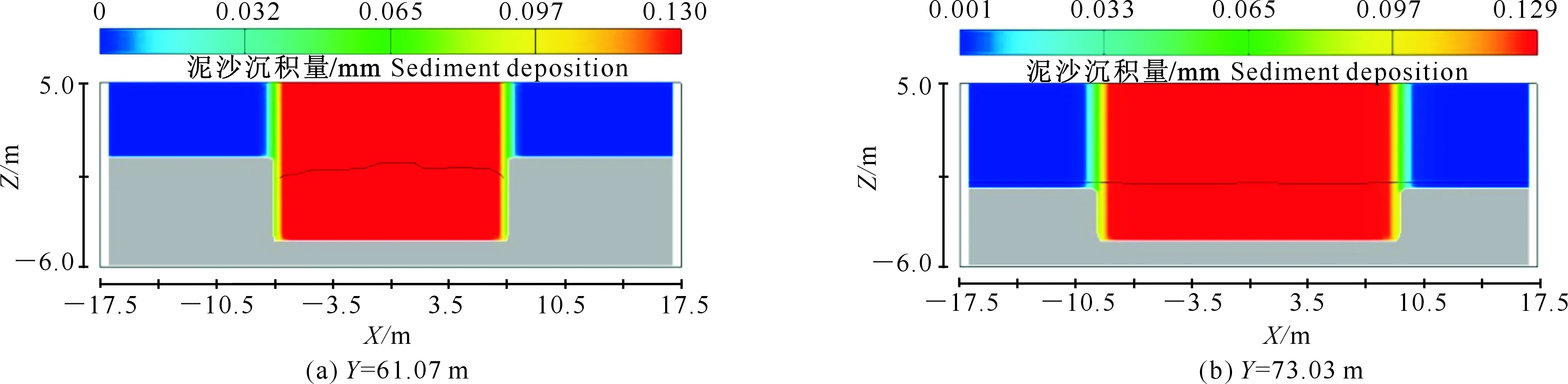
图9 牛角店输水工程渠底泥沙沉积正剖面图Fig.9 Positive section of sediment deposition at the bottom of water conveyance channel in Niujiaodian

2.4 模型验证

对于小型工程，往往不具备物理模型试验的条件，而一些处于设计阶段的工程，也同样缺乏相关的实测资料。本研究主要从水动力学角度，研究牛角店输水工程建设后可能存在的问题，由于模型主要用于工程建设前的论证，因此采用与类似资料进行对比分析的方法定性比较，以验证模型的合理性。

根据吉林省水利科学研究院陈永明等[29]对宽顶堰的试验结果及数值分析，在接近淹没出流的条件下，堰后回流区长度与工况堰顶水头的比值为1.41～1.54，宽顶堰接近淹没出流时的流场如图10所示。

图10 宽顶堰接近淹没出流时的流线图Fig.10 Streamline of broad crest weir near submerged outflow

牛角店模型中第二级挑坎后的出流情况与陈永明等[29]的试验结果相似，计算发现牛角店输水工程挑坎后的回流区长度与挑坎顶部水头的比值为1.42～1.56，说明模型的出流情况基本满足实际情况。

根据武汉水利电力学院张瑞瑾[30]对清水与挟沙水流紊动特性水槽试验结果的分析，挟沙水流的紊动强度较清水水流低，且在相对水深较小的区域内，挟沙水流紊动强度的降低效果更加明显。当水流紊动强度降低时，紊动耗散能量减小，水流流速加大，水面线降低，模型计算结果与张瑞瑾[30]对水槽试验现象的分析结果相符，说明该模型能够较好地应用于实际工程的模拟。

3 结 论

通过建立牛角店输水工程三维数学模型，以Flow-3D作为计算平台，按照水流是否挟沙及上游来水量设计8种工况，研究了阶梯明渠水流流速分布、水面线变化以及泥沙沉积等特性，并分析其对工程的影响，得到如下结论。

(1)流速分布及变化情况。清水条件下，水流整体流速随着上游水深降低而降低，最大流速出现在第一级挑坎挑射水流末端；挟沙条件下，由于水流的紊动作用减小，水流流速较对应上游水位清水条件下略有增加。明渠第二级阶梯流速整体偏大，工程施工过程中应考虑提升第二级阶梯混凝土底板的强度及抗冲刷性能。

(2)水面线变化情况。清水条件下，随着上游水深降低，水面线略有下降，在挑流水舌前有水跃现象；挟沙条件下，由于水流流速增大，水面线有明显下降。由于第二级阶梯侧墙略低，水体经过第一级挑坎会有溢出现象，施工过程中应当考虑适当增加侧墙高度。

(3)泥沙淤积情况。随着水位降低与计算时间增长，泥沙沉积厚度逐渐增加，且泥沙主要堆积在挑坎前和第三级阶梯上。为控制明渠泥沙淤积，在工程运行过程中需要采取合理的调度方式，增加坎前水流的冲沙能力，降低下游水位，以减少渠道泥沙淤积。