一道条件相互矛盾的中考试题

☉四川内江师范学院数学与信息科学学院 钟梦圆

☉四川内江师范学院数学与信息科学学院 刘成龙

☉四川内江师范学院数学与信息科学学院 董万平

试题命制是一个严肃而充满创造的系统工程.命题既要关注知识、能力、素养的考查，又要注重合适的难度、有效的信度和适当的区分度的设置，更要关注试题的严谨性.严谨性是数学的基本特征，它要求数学试题内容科学、表述准确、条件相容、问题明确等.中考作为初中阶段最重要的区域性考试，对试题命制有很高要求.但遗憾的是，在历年的中考命题中都会有试题因不严谨而出现错误.比如，2018年贵州省黔东南·黔南·黔西南中考数学第22题（下文简称第22题）第（Ⅱ）问就是一道错题.本文分析该试题出错的原因，并给出优化的方案及命题启示.

一、试题回放

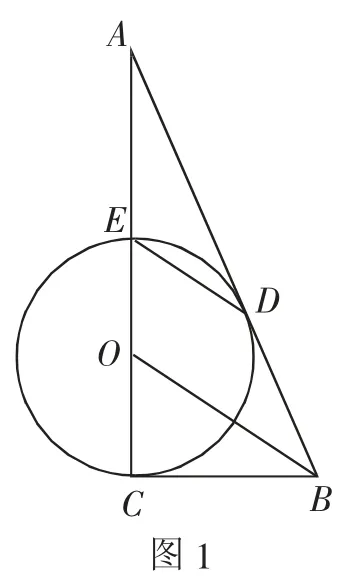
试题：（第22题）如图1所示，CE是⊙O的直径，BC切⊙O于点C，连接OB，作ED∥BO交⊙O于点D，BD的延长线与CE交于点A.

（I）求证：AB是⊙O的切线；

二、（Ⅱ）的六种解法

解法1：（命题组提供的参考答案）如图2，在Rt△ACB中，tan∠A=在Rt△OCB中，则于是

解法2：如图2，在Rt△ADO中，则AD=4，于是所以AE=

解法3：如图2，根据解法2可知AD=4，由切割线定理可得AD2=AE×（AE+2），即16=AE×（AE+2），解得AE=

解法4：如图2，由前文解法可知AD=4，BC=，所以BD=BC=

解法5：由图2可知S△ACB=S△AOD+2S△OCB，则

解法6：如图3，取DE的中点F，连接OF，过点D作DP⊥OE于点P.

易得OF为DE的中垂线.

六种解法呈现了五个不同的结果，为什么呢？我们不妨先看看解法中条件的使用情况：解法1、4、5、6中，两个条件均使用了；解法2、3仅使用了条件.疑问产生了：条件为什么没有用完呢？在使用相同条件时为什么会出现不同的答案呢？于是，我们可以大胆猜想试题有误.

三、试题错误分析

分析1：从角度入手，探索∠A、∠DEO的正切值间的关系

分析2：从面积入手，探索∠A、∠DEO的正切值间的关系

分析3：从平行边入手，探索∠A、∠DEO的正切值间的关系

过程略.

从上面的分析可知：tan∠A与tan∠DEO之间的关系为：但试题条件中两个正切值之间不满足这一关系，造成条件之间相互矛盾，从而导致试题错误.实际上在这一关系下，tan∠A与tan∠DEO这两个条件只需一个即可完成试题的解答，这为试题的优化提供了方向.

四、试题优化

优化后的条件间不再相互打架，实现了内在的和谐统一.

五、命题启示

命题工作责任重大，不容许出现丝毫错误.如何才能命制出一道道质量较高的试题呢？我们认为至少要做到四个方面：一是命题者要学习命题相关理论——命题工作的方向保障，提高理论认识，用命题理论指导命题实践，做好命题工作的顶层设计；二是命题者要提高学科素养——命题工作的动力源泉，提高对数学问题的认识与理解，切实做好命题工作的现实创新；三是命题者要启动磨题程序——命题工作的生命线，通过对试题多次、反复打磨，不断优化素材呈现形式和条件表达方式，充分把握试题的严谨性、合理性和科学性；四是命题者要建立试做机制——命题工作的必然要求，试做是磨题的延续，是命题工作的最后一个环节，通过试做感受试题的难度、发现试题的不合理因素，便于及时纠正和优化，为最终呈现一道道高质量试题把好出炉关.诚然，命制高质量试题不易，但理应成为命题者们不懈的追求和使命.