翼身融合民机典型PRSEUS受压壁板屈曲及渐进损伤分析

张永杰，吴莹莹，朱胜利，王斌团，谭兆光，袁昌盛

1. 西北工业大学 航空学院，西安 710072 2. 航空工业 第一飞机设计研究院，西安 710089 3. 上海飞机设计研究院，上海 201210

翼身融合布局[1-12]在下一代大型民用飞机气动、油耗、噪声等方面优势明显，然而此特殊布局型式也给结构设计及其可实现性带来了巨大挑战，尤其是其非圆形截面增压机身结构导致的承载效率低、稳定性差、增重等问题[13-28],如图1所示[13]，已经成为制约翼身融合布局民机发展的重要因素。为此，美国波音公司在NASA-Langley研究中心的协助下将集成化设计思想引入到翼身融合多舱室机身结构设计中，提出了拉挤杆缝合高效一体化结构(Pultruded Rod Stitched Efficient Unitized Structure, PRSEUS)[29-49]，如图2所示[43-46]。

本文从PRSEUS结构的物理实体模型入手，构建了隔框和长桁元件之间的贯穿支撑几何关系，提出了由蒙皮、隔框方向止裂带、长桁方向止裂带、长桁翻边、隔框翻边等组成的一体化缝合结构偏置参考面建模方法，提高了PRSEUS受压壁板的有限元模型精度；开展了非线性屈曲分析的网格收敛性分析方法研究，综合考察了网格尺度对屈曲特征值、非线性屈曲行为等多种因素的影响，获得了PRSEUS受压壁板非线性屈曲分析最佳网格尺度；开展了非线性屈曲损伤分析方法研究，提出了最小屈曲特征值、几何节点偏移以及最小屈曲特征值-几何节点偏移组合等3种初始缺陷引入方法，以及基于纤维与基体损伤本构关系的典型PRSEUS受压壁板非线性屈曲渐进损伤演化分析方法，为翼身融合布局民机PRSEUS结构的稳定性设计与损伤分析提供技术手段。

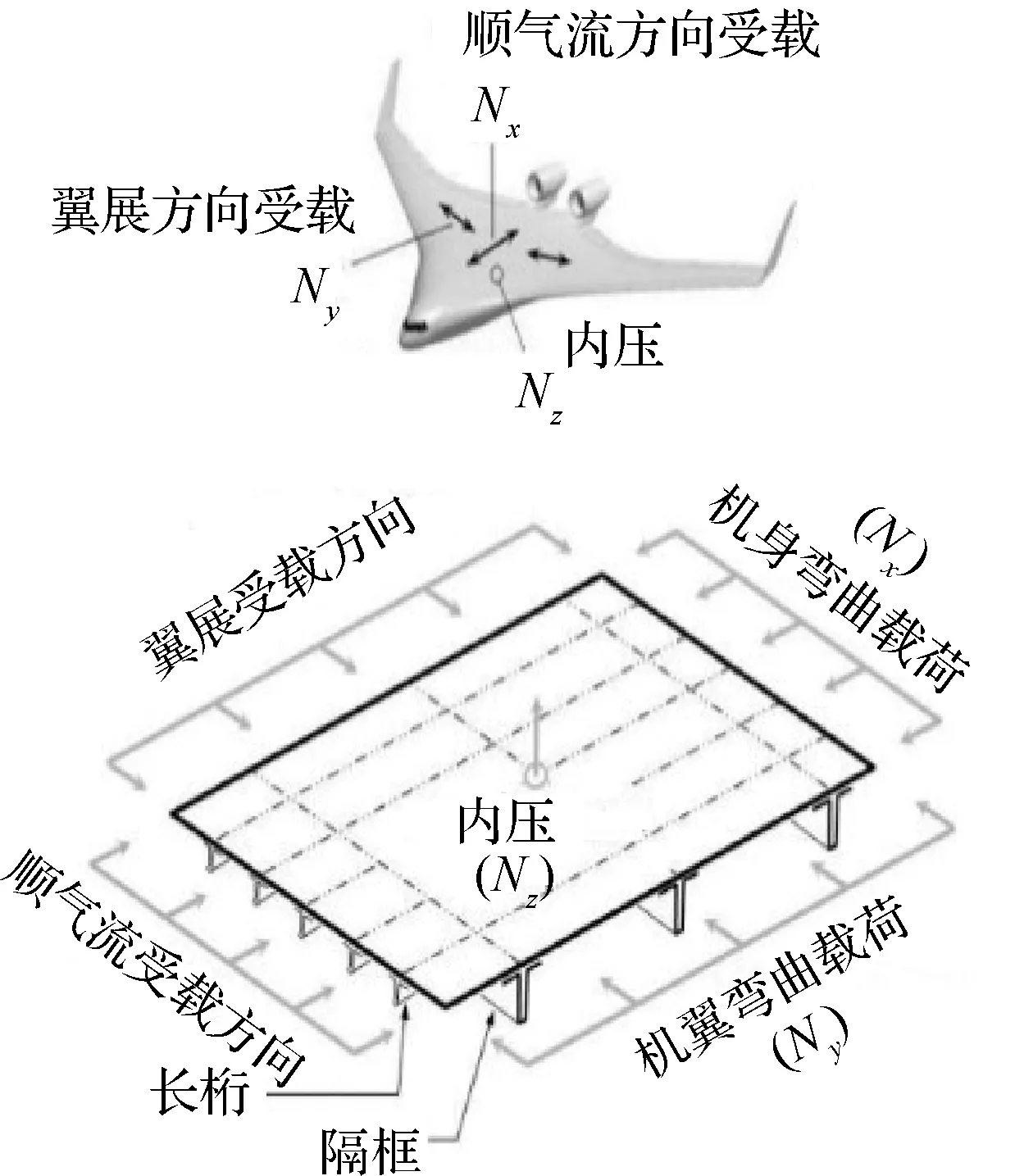
图1 翼身融合中央机体受载示意图[13]Fig.1 Schematic diagram of blended-wing-body fuselage loading characteristics [13]

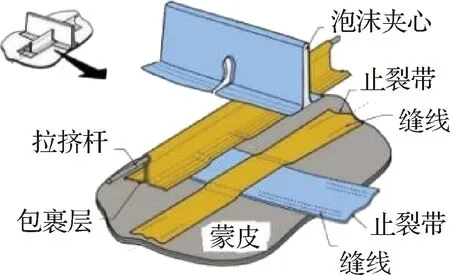
图2 PRSEUS结构示意图[43-46]Fig.2 Schematic diagram of PRSEUS structure [43-46]

1 PRSEUS结构特性

PRSEUS结构由蒙皮、长桁和隔框3种基本元件组成(如图2所示)，机翼传来的弯矩主要由隔框方向部件承受，机身传来的弯矩主要由长桁方向部件承受，客舱增压载荷则由蒙皮、长桁和隔框组合而成的壁板承受。长桁上端布有单向高模量碳纤维拉挤杆，拉挤杆外部包裹有碳纤维复合材料包裹层，通过底部翻边与止裂带和蒙皮缝合在一起。隔框与长桁互相垂直，由泡沫夹心和碳纤维复合材料包裹层组成，也通过底部翻边与止裂带和蒙皮缝合在一起。如图2所示，虚线部分为缝线位置，底部灰色部分为蒙皮，黄色部分为长桁外部包裹层和长桁方向止裂带，浅蓝色部分为隔框包裹层和隔框方向止裂带。PRSEUS结构中，以零度纤维为主的高模量拉挤杆位于长桁部件上部，距离底部蒙皮较远，这种结构布置不仅提高了中性轴高度，而且增加了长桁方向部件的局部刚度和稳定性，提高了PRSEUS整体壁板的抗弯能力。隔框中部采用泡沫夹心材料，不仅减轻了结构重量，而且提高了隔框方向的承压和抗弯能力。拉挤杆穿过隔框下部，为了防止长桁和隔框交接处发生损伤，此处专门进行了局部补强处理，确保了双向传力路径的连续性，充分体现了PRSEUS结构的立体承载模式。PRSEUS结构的包裹层、翻边、止裂带和蒙皮均采用AS4碳纤维复合材料[47]，长桁上端的拉挤杆由T800碳纤维和3900-2B树脂组成[47]；隔框泡沫夹心使用的是Rohacell泡沫[47]。

2 典型PRSEUS受压壁板屈曲分析

2.1 典型PRSEUS受压壁板有限元模型

1) 几何模型

本文中选取含双隔框的PRSEUS壁板[49-50]作为典型PRSEUS受压结构进行屈曲和渐进损伤分析。如图3所示[49]，双隔框PRSEUS壁板由2 个隔框和15 个长桁组成，长约2 286.0 mm(90 in)，宽约762.0 mm(30 in)，其中隔框间距约508.0 mm(20 in)，长桁间距约152.4 mm(6 in)。如图4所示，隔框泡沫夹心高度为152.40 mm，厚度为12.70 mm，隔框下部止裂带及翻边总宽度为101.60 mm。如图5所示，长桁总高度为37.85 mm，上端拉挤杆直径为9.53 mm，长桁下部止裂带及翻边宽度为86.36 mm。

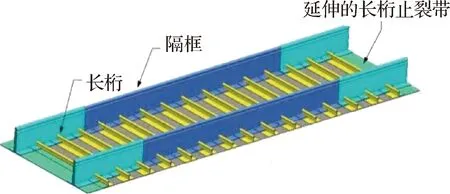
图3 双隔框PRSEUS结构几何模型[49]Fig.3 Geometrical model of two-frame PRSEUS structure[49]

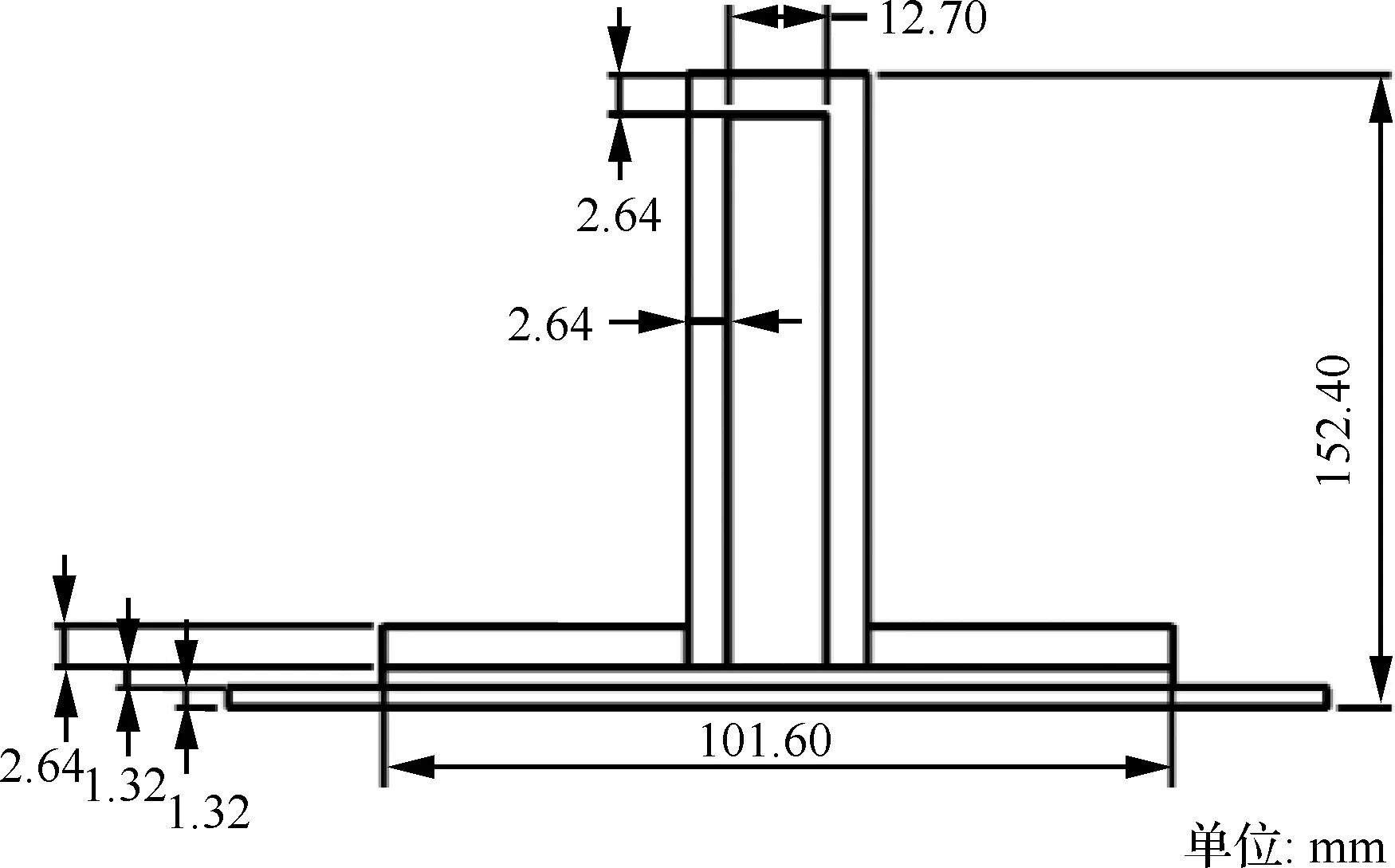
图4 PRSEUS受压壁板隔框截面Fig.4 Frame cross-section of compressed PRSEUS panel

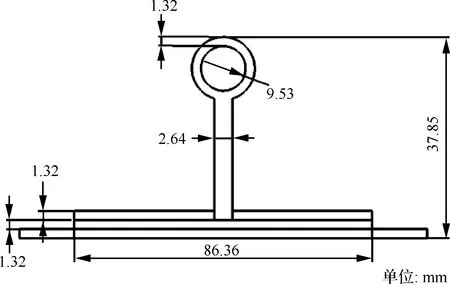
图5 PRSEUS受压壁板长桁截面Fig.5 Stringer cross-section of compressed PRSEUS panel

2) 材料属性

在双隔框PRSEUS壁板结构中，包裹层、翻边、止裂带和蒙皮均由AS4碳纤维复合材料层合板构成[50-51]，单个层合板包含9 层铺层，其铺层顺序为[45/-45/0/0/90/0/0/-45/45]T，其中对于蒙皮、隔框包裹层、隔框止裂带和翻边，其0°纤维方向均平行于隔框方向；对于长桁包裹层、长桁止裂带和翻边，其0°纤维方向均平行于长桁方向。层合板总厚度为1.320 8 mm，其中0°、45°、90°所占的厚度比例分别为44%、44%、12%。长桁上端的拉挤杆由T800碳纤维和3900-2B树脂组成[52]；隔框方向的泡沫夹心是Rohacell泡沫材料[52]。双隔框PRSEUS壁板结构各个部件所包括层合板数目如表1所示，复合材料单层板的材料属性如表2所示[47]，长桁上端拉挤杆和隔框泡沫夹心的材料属性如表3所示[47]。

3) 参考面偏置

如图6所示，在双隔框PRSEUS壁板有限元模型中，蒙皮、长桁/隔框包裹层、翻边、止裂带均采用一阶壳单元模拟，长桁上端单向复合材料拉挤杆和隔框中部泡沫夹心均采用一阶体单元来模拟。考虑到PRSEUS结构的一体化缝合和共固化加工工艺[49-52]对于各元件的法向刚/强度增强和组合支撑效应，为了提高模型的准确性，本节对蒙皮、长桁/隔框包裹层、翻边、止裂带等处所采用壳单元的相对位置和刚性参考面偏置进行了详细讨论。

表1 PRSEUS板中的复合材料层合板数目

表2 复合材料力学特性[47]Table 2 Mechanical properties of composite material[47]

表3 隔框泡沫夹心层和长桁材料特性[47]

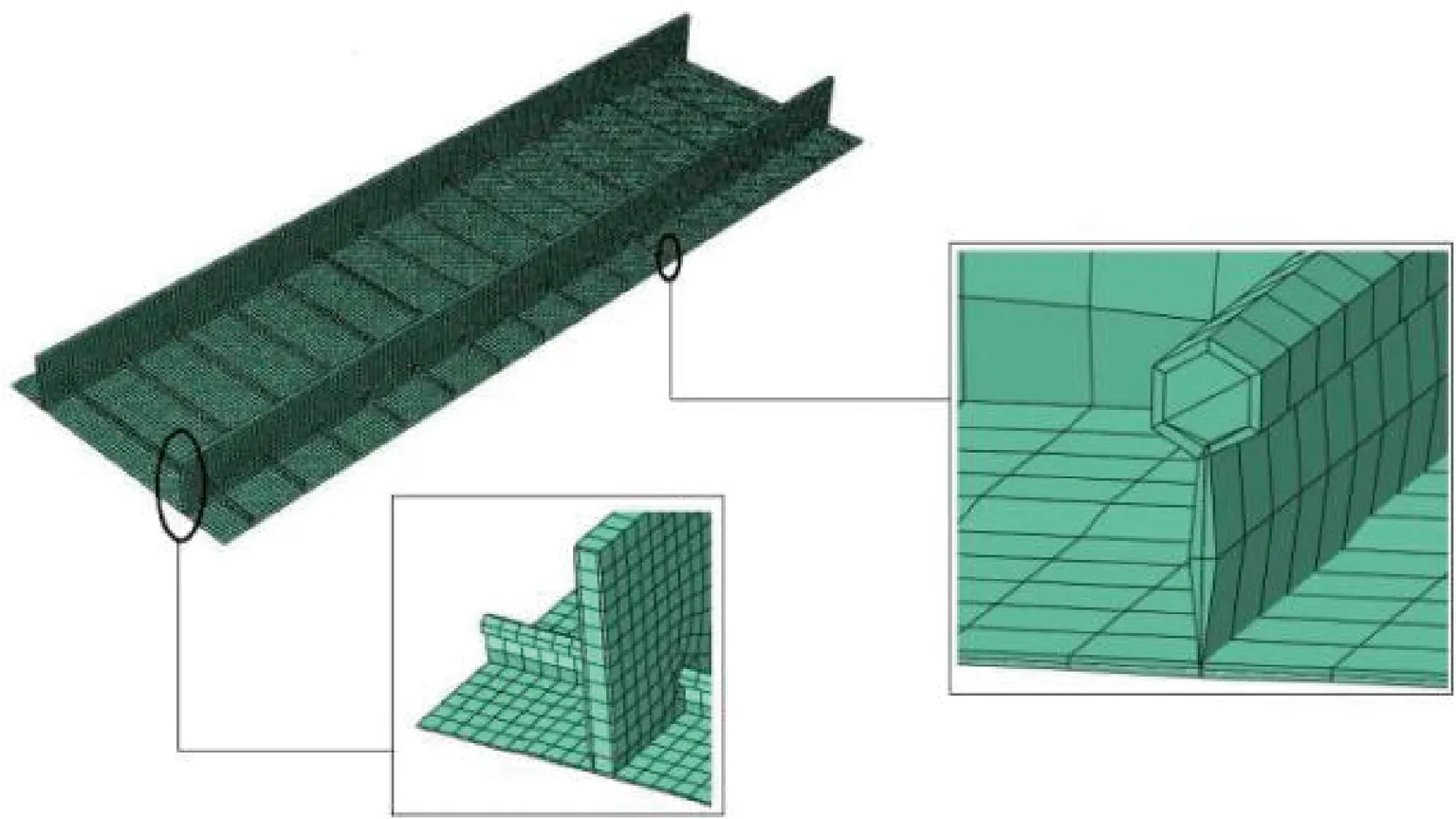
图6 双隔框PRSEUS壁板有限元模型Fig.6 Two-frame PRSEUS panel finite element model

有限元建模过程中，壳单元偏置量通常是指初始中性面偏移量与壳总厚度的比值，一般默认的刚性参考面均为各元件壳单元的中性面，但是针对本文利用一体化缝合和共固化工艺制造[47,52]的双隔框PRSEUS壁板结构，直接采用默认的几何中性面作为刚性参考面的做法无疑将会带来较大的建模误差。为此，这里充分考虑了双隔框PRSEUS壁板结构中蒙皮、长桁/隔框包裹层、翻边、止裂带等元件的几何叠加、刚度折算、缝合加强等因素，结合薄壁加筋壁板刚度设计中常用的刚性参考面设置方式(即：0代表刚性参考面设置在中心面上，无偏置；0.5代表刚性参考面设置在上表面，向上偏置一半厚度；-0.5代表刚性参考面设置在下表面，向下偏置一半厚度)，对上述元件的壳单元刚性参考面位置进行了多种组合分析，如图7所示；通过与文献[53]的屈曲分析结果进行对比(2.3节给出)，最终确定蒙皮的偏置量取0(即蒙皮壳单元的刚性参考面设置在蒙皮中心面)，长桁和隔框包裹层的偏置量取-0.5(即包裹层壳单元的刚性参考面设置在包裹层下表面)，隔框翻边和止裂带的偏置量取-0.5(即隔框翻边和止裂带壳单元的刚性参考面设置在隔框翻边和止裂带下表面)，长桁翻边和止裂带的偏置量取-0.5(即长桁翻边和止裂带壳单元的刚性参考面设置在长桁翻边和止裂带下表面)。

4) 几何支撑关系

表1给出的蒙皮、长桁/隔框包裹层、翻边、止裂带等不同元件所用层合板数目，是通过设置复合材料壳单元的铺层数来实现的。如图8所示，红色线框指示出了隔框翻边和止裂带铺设区域，绿色线框指示出了长桁翻边和止裂带铺设区域。其中隔框翻边铺层数量为18 层，隔框止裂带铺层数量为9 层，长桁翻边和止裂带铺层数量均为9层。此外，为了更加精确模拟双隔框PRSEUS结构的受压屈曲行为，结合PRSEUS结构制造工艺[47,52]，此处给出了长桁与隔框元件的相互贯穿支撑关系(如图9所示)，并对长桁方向的拉挤杆、包裹层和隔框方向泡沫夹心、包裹层等局部网格进行了细化和对应性处理。

图7 PRSEUS结构模型参考面的设置示意图Fig.7 Schematic diagram of PRSEUS structure model reference surface setting

图8 双隔框PRSEUS壁板有限元模型不同厚度元件区域示意图(外向俯视图)Fig.8 Schematic of different thickness element regions of two-frame PRSEUS panel finite element model (top view with external direction)

5) 载荷和边界条件设置

参考屈曲试验[50]的加载和边界条件情况，本文双隔框PRSEUS受压壁板结构的载荷和边界条件设置如图10所示。需要指出的是，特征值分析中施加的是力载荷，非线性分析中施加的载荷是位移载荷，并以特征值屈曲分析获得的第1阶模态作为初始扰动引入到非线性屈曲分析中。图中：总体坐标系的x、y、z方向分别设置为长桁方向、蒙皮外法线方向和隔框方向。

图9 双隔框PRSEUS结构有限元模型局部贯穿支撑关系Fig.9 Local correlation relationship of two-frame PRSEUS panel finite element model

图10 双隔框PRSEUS结构载荷和边界条件设置Fig.10 Settings of loading and boundary constraint in two-frame PRSEUS panel

2.2 双隔框PRSEUS受压壁板网格收敛性分析

为了确保屈曲分析的精度和收敛性，同时降低计算量，本节开展了一系列的网格收敛性分析，通过分析不同网格尺度下的线性特征值屈曲和非线性屈曲计算结果，给出了双隔框PRSEUS受压壁板的屈曲分析最佳网格尺度。

参考屈曲试验和相关文献资料[49-53]，在 4.23～31.75 mm之间选取了11 种不同网格尺度对双隔框PRSEUS受压壁板结构进行了剖分，并进行了特征值屈曲和非线性屈曲计算，得到的前6阶特征值如表4和图11所示(网格数量随网格尺度变化如图12所示)，得到的非线性屈曲载荷-位移曲线如图13所示。综合分析，可得如下结论：

1) 通过不同网格尺度下特征值屈曲计算结果可以看出，随着网格尺度的增大，前6阶屈曲特征值的波动变大，当网格尺度小于15.24 mm时，前6阶 屈曲特征值的波动较小，当网格尺度小于8.46 mm 时，前6阶屈曲特征值的波动趋于平缓。

2) 通过不同网格尺度下非线性屈曲计算结果可以看出，当网格尺度小于19.5 mm时，非线性屈曲载荷-位移曲线较为集中，屈曲非线性行为较为一致。

3) 通过不同网格尺度下的网格数量变化图可以看出，当网格尺度大于10.16 mm时，网格数量的下降趋势变得平缓，计算量趋于稳定。

表4 不同网格尺度前6阶特征值屈曲载荷Table 4 Buckling load of the first six modes in models with different mesh sizes

综合考虑以上不同网格尺度下特征值屈曲和非线性屈曲计算得到的前6阶特征值、载荷-位移曲线、网格数量等变化趋势，结合网格剖分处理和局部细节特征刻画的难易程度，本文选取12.7 mm 作为双隔框PRSEUS受压壁板的屈曲分析最佳网格尺度。

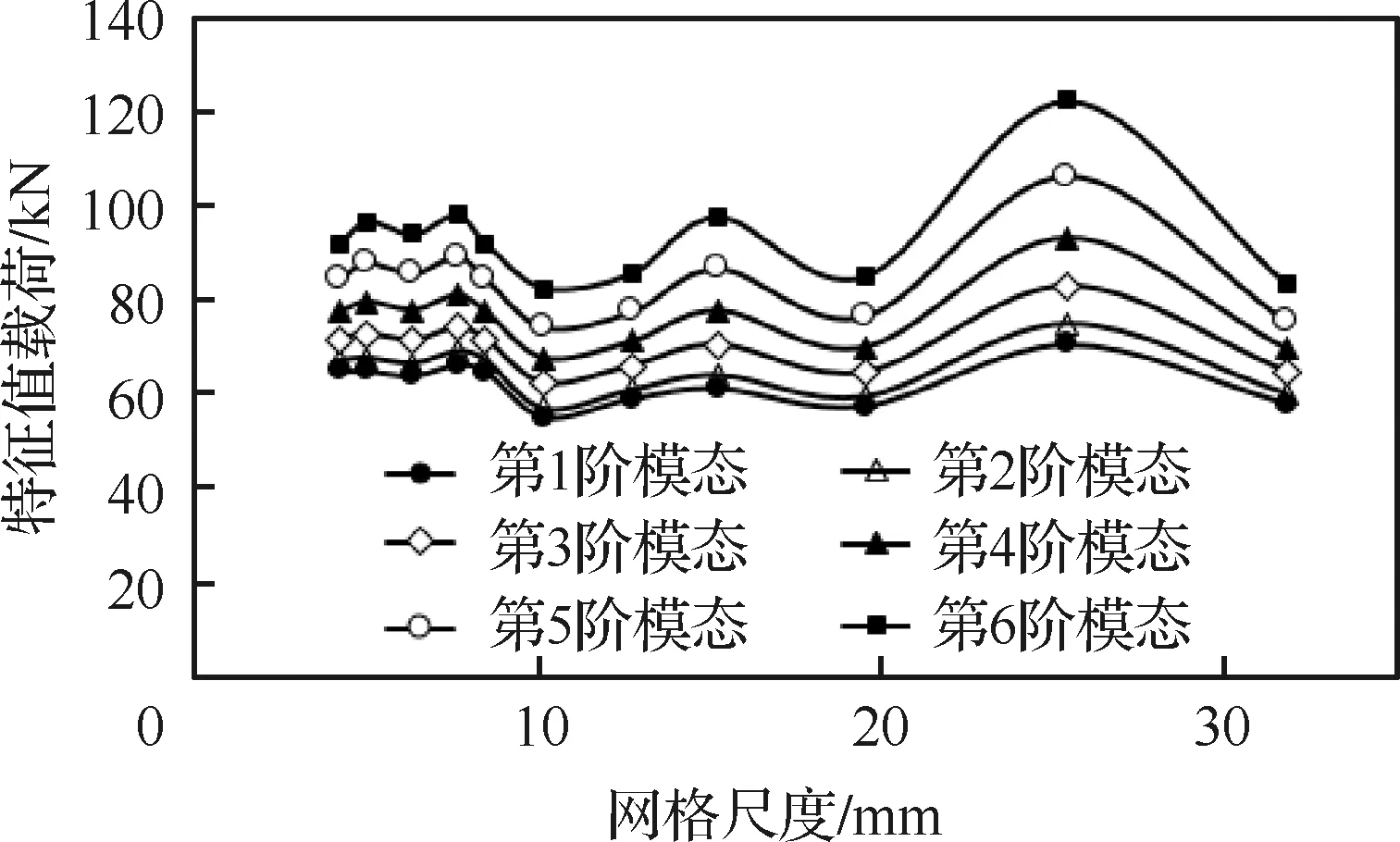
图11 前6阶特征值屈曲载荷随网格尺寸变化Fig.11 Variation of the first six eigenvalue buckling load with mesh size

图12 不同网格尺度下的网格数量变化Fig.12 Variation of number of elements with different mesh sizes

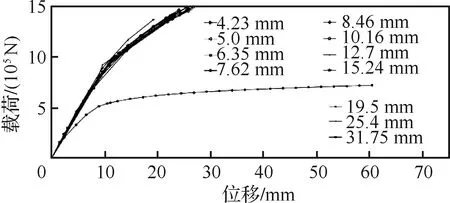
图13 不同网格尺度下的非线性分析载荷-位移曲线Fig.13 Load with displacement curves of models for different mesh sizes in nonlinear analyses

2.3 双隔框PRSEUS受压壁板特征值与非线性屈曲分析结果

1) 特征值屈曲分析结果与文献对比

如表5所示，在12.7 mm最佳网格尺度下，将本文第1阶特征值分析结果与文献[53]的分析结果进行了对比，第1阶特征值屈曲载荷和屈曲模态均较为吻合。

2) 非线性屈曲分析结果与试验对比

如表6所示，在12.7 mm最佳网格尺度下，将本文非线性屈曲分析结果与文献[50]的试验结果进行了对比分析。通过几个关键载荷历程下的面外位移误差分析可以看出，在双隔框PRSEUS受压壁板经历的非线性屈曲响应过程中，本文非线性屈曲计算结果能够与试验结果保持趋势一致，但存在一定的面外位移误差；主要由于未考虑几何缺陷和损伤破坏对非线性屈曲分析的影响，所以无法完全反映双隔框PRSEUS受压壁板的非线性屈曲损伤行为。

表5 特征值屈曲分析结果与文献[53]结果对比

Table 5 Comparison of eigenvalue buckling analysis and experiment results

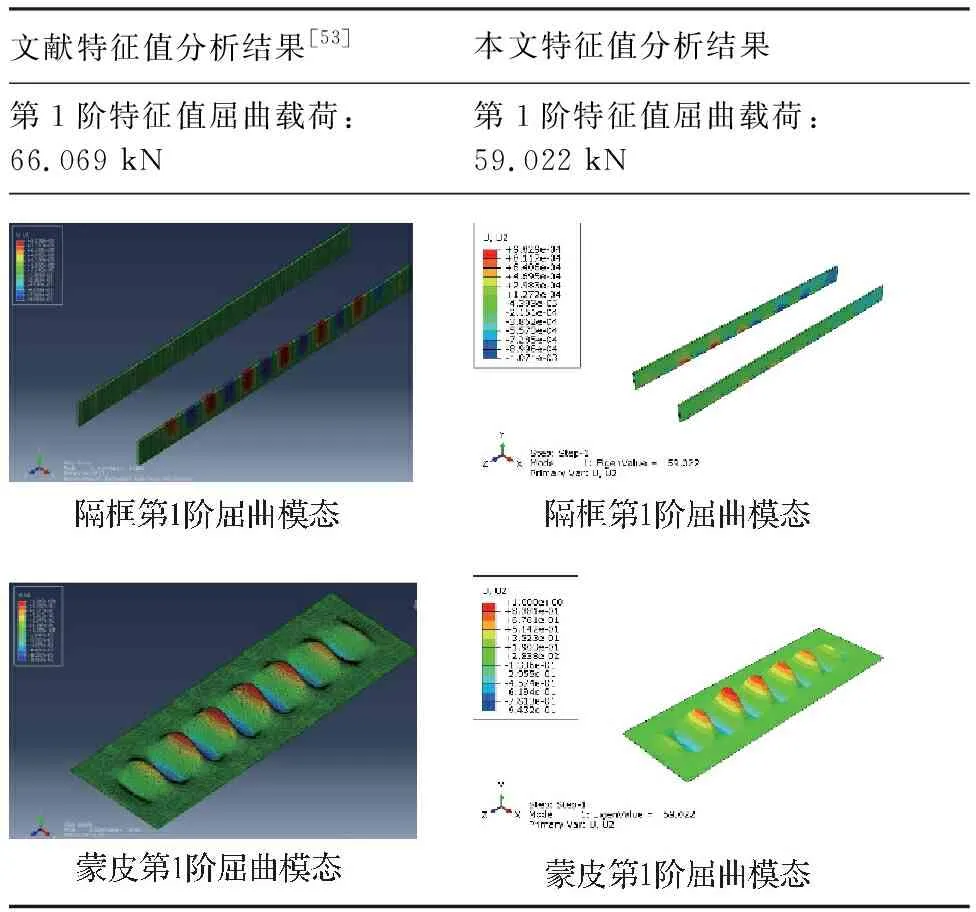
文献特征值分析结果[53]本文特征值分析结果第1阶特征值屈曲载荷:66.069 kN第1阶特征值屈曲载荷:59.022 kN

3 双隔框PRSEUS受压壁板渐进损伤分析

为了更加准确地模拟双隔框PRSEUS受压壁板的非线性屈曲响应，本节主要讨论双隔框PRSEUS受压壁板的渐进损伤分析方法和几何缺陷引入方法。渐进损伤分析方法是通过开发刚度衰减子程序完成的，几何缺陷是通过引入特征值初始缺陷、节点偏移初始缺陷及其两者组合等3种方式完成的。最后，通过与文献[50]试验结果进行对比，验证了本文提出的双隔框PRSEUS受压壁板非线性屈曲渐进损伤分析方法和几何缺陷引入方法具有较高的精度和工程应用价值。

3.1 渐进损伤判据

1) 本构关系

对于正交各向异性复合材料而言，其刚度矩阵具有对称阵，只需确定9个本构参数，即

(1)

式中：E1为1方向的弹性模量；E2为2方向的弹性模量；G12为1-2平面内的剪切模量；G23为2-3平面内的剪切模量；μ12、μ21和μ23为泊松比。

2) 失效准则

复合材料的失效模式一般分为2种：基体失效和纤维失效，本文采用的是基于应变的失效准则。其中，基体材料的失效判据为

(2)

纤维材料的失效判据为

(3)

式(2)和式(3)中：

(4)

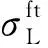
于是，可以得到描述损伤演化过程的损伤变量dm和df为

(5)

(6)

式中：Lc为单元的特征长度；Wm为破坏模式下基体材料破坏所需的耗散能；Wf为破坏模式下纤维材料破坏所需的耗散能;Gm为基体断裂能；Gf为纤维断裂能。

将式(5)和式(6)中的损伤变量dm和df引入到复合材料刚度矩阵中，折减后的刚度矩阵表达为

Cdamaged=

(7)

式中：α=1-df;β=1-dm。

3.2 双隔框PRSEUS受压壁板渐进损伤分析方法

如3.1节所述，伴随结构加载，当复合材料单元应变达到基体/纤维材料失效的临界应变值时，结构开始出现损伤，需对单元刚度进行折减运算。根据损伤变量，计算折减后的刚度矩阵，进而计算单元新的应力/应变状态，并更新状态变量完成损伤失效判别。损伤失效判别可采用UMAT (User-defined material)用户材料子程序来实现，刚度衰减子程序的具体流程如图14所示。

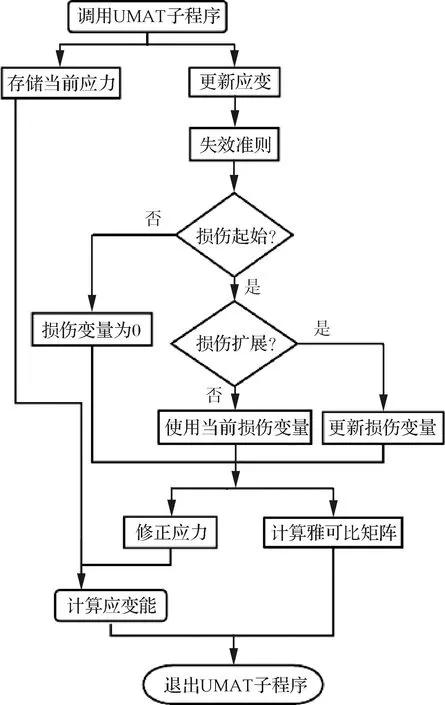
图14 刚度衰减子程序流程图Fig.14 Flow chart of stiffness decrease subroutine

针对纤维和基体的2种损伤,需要给出每种损伤模式下的断裂能以判断损伤演化趋势,参考文献[54],此处纤维断裂能取为12.5 N/mm,基体断裂能取为1 N/mm。本文所采用的复合材料层合板强度如表7所示[47]。

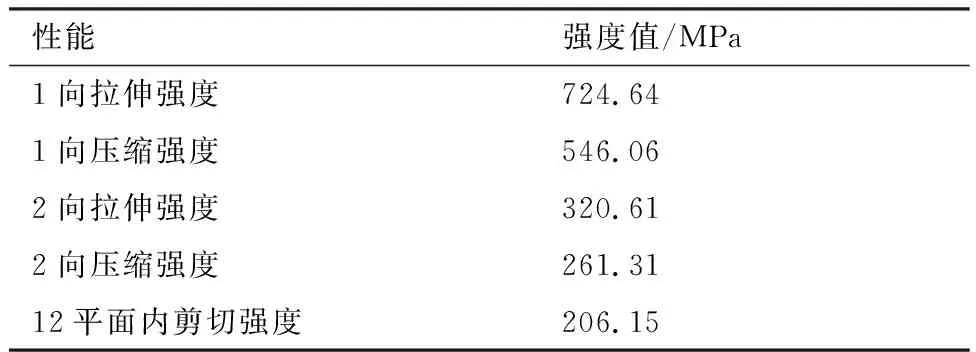
表7 复合材料层合板强度值[47]Table 7 Strength criteria of composite stack[47]

3.3 引入初始缺陷的非线性屈曲渐进损伤分析

为了充分反映双隔框PRSEUS受压壁板的初始几何特征，更加准确地模拟双隔框PRSEUS受压壁板的非线性屈曲试验过程，本节采用了3种初始缺陷引入方法：第1种是以第1阶特征值屈曲模态的1%作为初始缺陷引入[55]；第2种是以几何节点偏移方式引入初始缺陷[50,55]；第3种是本文提出的，即将上述2种方式进行组合引入初始缺陷。其中，几何节点偏移量采用的是双隔框PRSEUS受压壁板屈曲试验前获取的试件法向不平整量Z，如图15所示[50]，其法向位移最大值为0.508 mm(0.02 in)(注：板两侧红色的线表示应变片的引出导线，不是板的表面)。

初始缺陷引入流程如图16所示，表8和表9分别给出了3种初始缺陷损伤引入后最大载荷下非线性屈曲渐进损伤分析结果及其与试验结果对比。图17给出了3种初始缺陷引入方式下的非线性屈曲载荷-位移图。从引入初始缺陷后的非线性屈曲渐进损伤分析结果可以看出：

1) 通过采用渐进损伤分析方法和引入3种初始缺陷，能够更加准确地跟踪双隔框PRSEUS受压壁板试验的非线性屈曲响应行为，能够更加准确地模拟其损伤累积和演化过程。

图15 试验开始前的板面外位移[50]Fig.15 Out-of-panel displacement before test[50]

图16 引入初始缺陷程序流程图Fig.16 Flow chart of initial imperfection introduction

表8 3种初始缺陷损伤引入后最大载荷下的非线性屈曲渐进损伤分析结果对比

Table 8 Comparison of results of nonlinear progressive buckling analysis with three introducing imperfection methods at the maximum load

续表

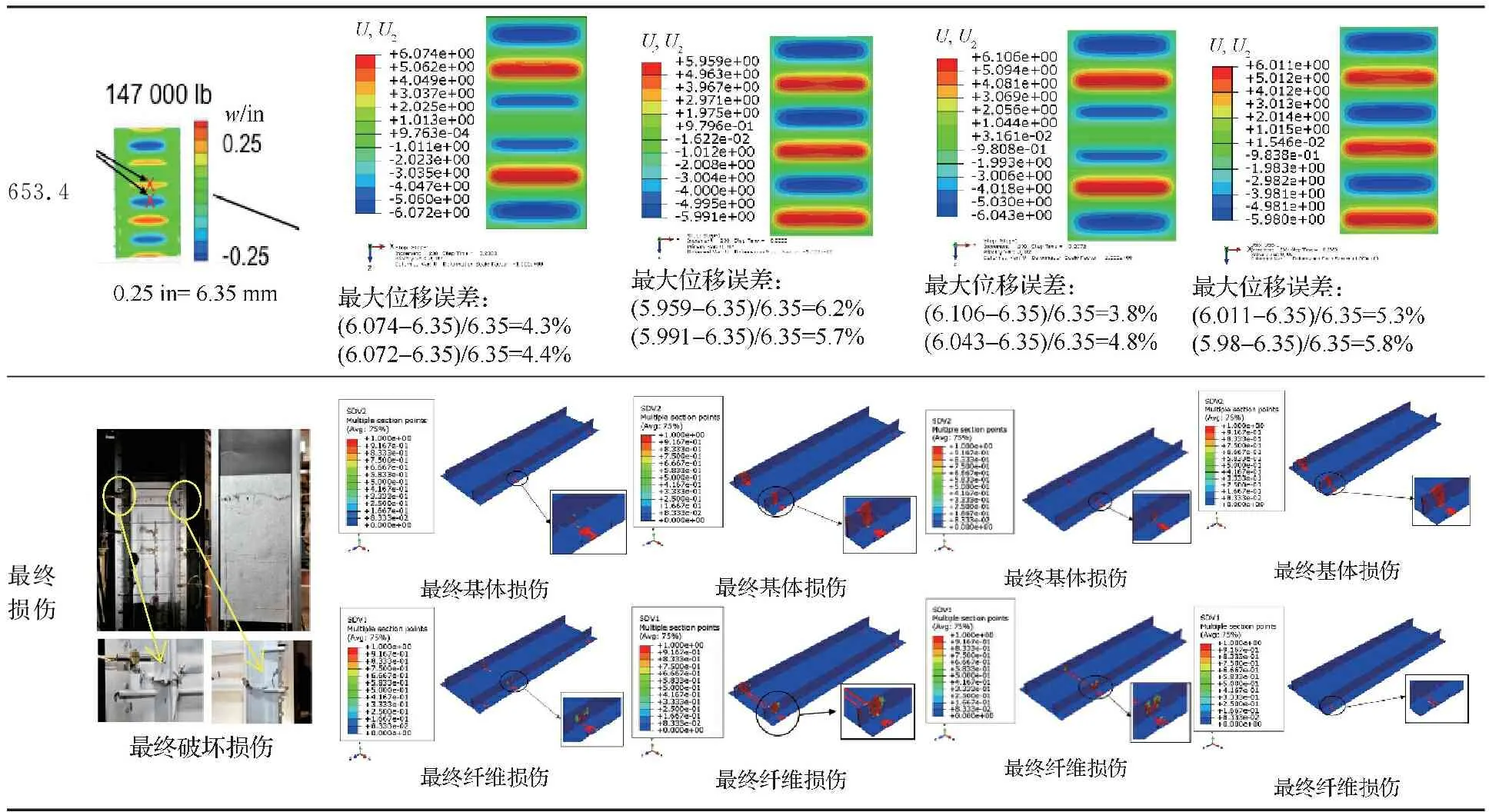
表9 3种初始缺陷引入方式的渐进损伤分析结果与试验结果对比Table 9 Comparison of nonlinear progressive buckling analysis results with three introducing imperfection methods and test

续表

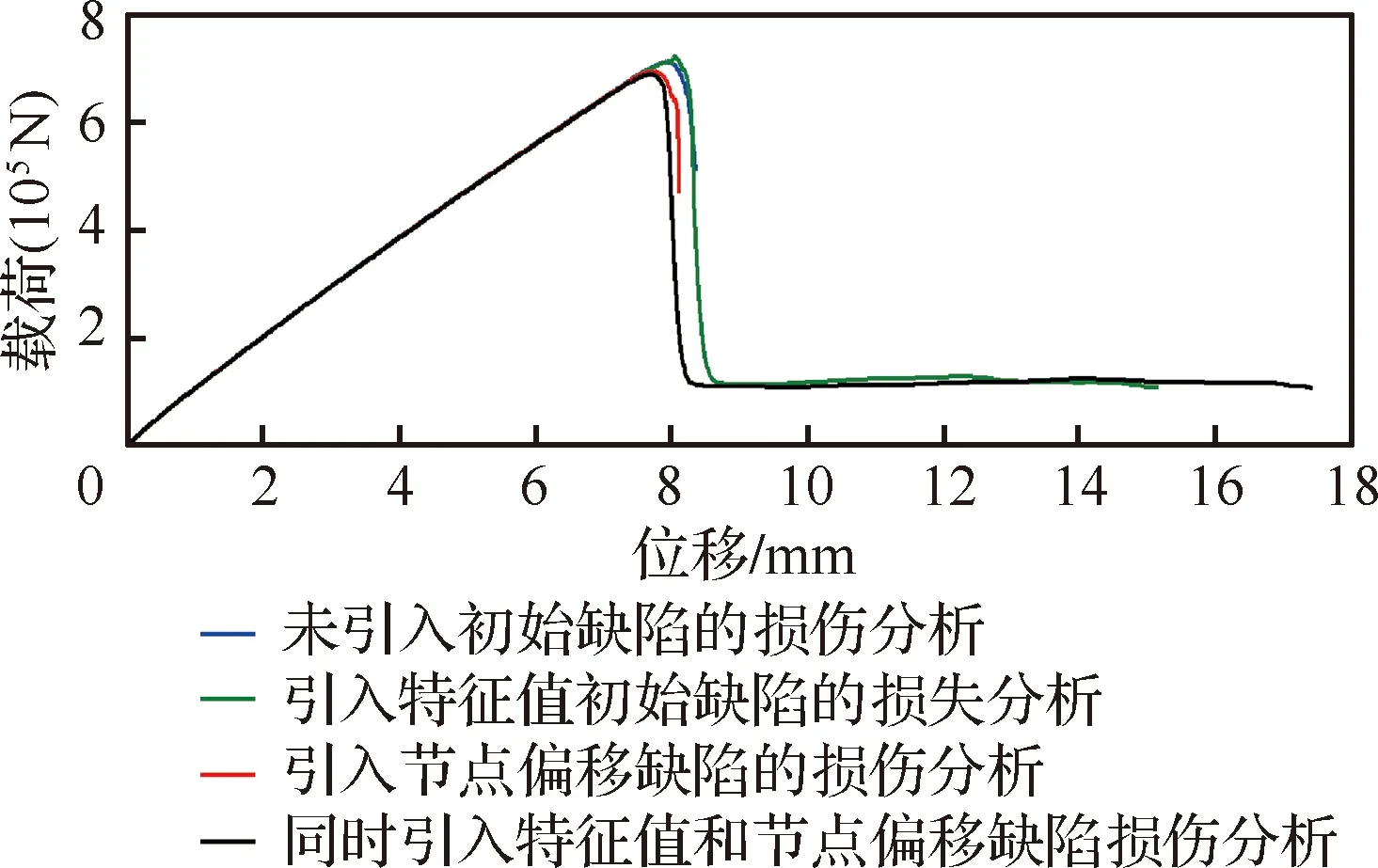
图17 3种初始缺陷引入方式的非线性屈曲载荷-位移图Fig.17 Nonlinear bucking load vary with displacement in three introducing imperfection methods

2) 在最大载荷作用下，蒙皮的法向屈曲变形较大，蒙皮纤维和基体的应变较大，初始损伤在蒙皮边缘出现；最终大面积损伤发生在隔框腹板区域；结合损伤的发展过程和趋势，可以判定双隔框PRSEUS受压壁板的屈曲损伤模式是由蒙皮结构引发、导致承压方向隔框垮塌，而最终压溃破坏的；所以应提高蒙皮和隔框元件的刚度和稳定性。

3.4 3种初始缺陷引入方式的渐进损伤分析结果与试验结果对比

表9给出了3种初始缺陷损伤引入后的非线性屈曲渐进损伤分析过程结果与试验结果的对比，可以看出：在双隔框PRSEUS受压壁板的初始屈曲阶段，未引入初始缺陷的损伤分析存在较大的计算误差，不能准确模拟初始屈曲行为，采用组合最小特征值和节点偏移初始缺陷的引入方式能够更加准确地模拟双隔框PRSEUS受压壁板的法向变形；在双隔框PRSEUS受压壁板的中后期屈曲阶段，采用节点偏移初始缺陷的引入方式能够更加准确地模拟双隔框PRSEUS受压壁板的法向变形。表10给出了3种初始缺陷损伤引入后的非线性屈曲渐进损伤分析最大载荷与试验结果的对比，可以看出：采用最小特征值和节点偏移组合式初始缺陷的引入方式能够更加准确地捕捉非线性屈曲最大载荷。

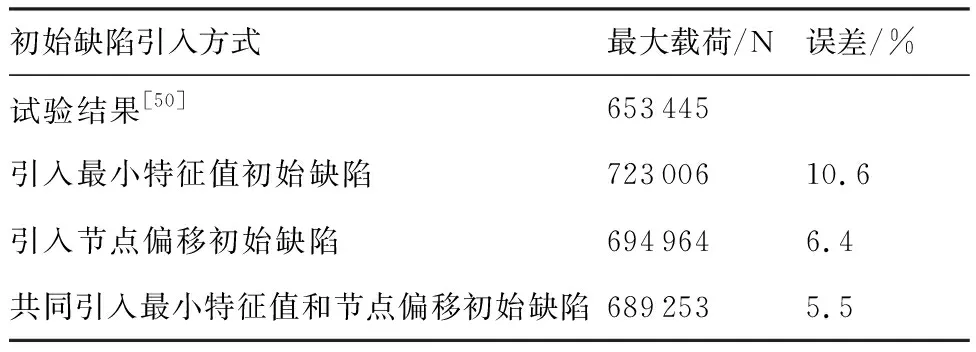
表10 3种初始缺陷引入方式下渐进损伤分析最大载荷与试验结果对比

4 结 论

为解决翼身融合布局民机非圆截面机身结构承载效率低和稳定性差等问题，NASA和波音公司共同提出了PRSEUS结构设计方案。本文针对典型PRSEUS受压壁板结构，提出了线性/非线性屈曲及渐进损伤分析方法，并通过屈曲试验数据验证了该方法的精度和准确性，总结如下：

1) 通过提出综合考虑PRSEUS结构组成元件几何关系和偏置参考面的建模方法，较为细致地刻画了模型的几何特征，有效提高了双隔框PRSEUS受压壁板的有限元模型精度。

2) 通过提出综合考虑屈曲特征值、非线性屈曲载荷-位移曲线、网格数量等多因素的网格收敛性分析方法，获得了双隔框PRSEUS受压壁板屈曲分析的最佳网格尺度，能够在确保计算精度和收敛性的基础上，降低计算量，有效提高了双隔框PRSEUS受压壁板非线性屈曲分析的计算效率。

3) 通过提出最小屈曲特征值、几何节点偏移以及最小屈曲特征值-节点偏移组合式等3种初始缺陷引入方法，充分反映了几何缺陷对双隔框PRSEUS受压壁板的屈曲行为影响，有效提高了双隔框PRSEUS受压壁板非线性屈曲/损伤分析的计算精度。

4) 通过提出基于纤维与基体本构关系的渐进损伤分析方法，较为准确地跟踪和捕获了双隔框PRSEUS受压壁板非线性屈曲响应和损伤演化过程，有效提高了双隔框PRSEUS受压壁板非线性屈曲损伤分析精度；通过与试验结果对比,验证了本文提出的典型PRSEUS受压壁板结构非线性屈曲/渐进损伤分析方法的准确性和工程应用价值;也为翼身融合布局民机PRSEUS结构的稳定性/损伤分析与设计提供了基础方法和技术手段。