基于单片机的旋转倒立摆控制系统研发

李晓豪，李 鑫

（常熟理工学院 电气与自动化工程学院，江苏 常熟 215500）

旋转倒立摆系统是一个非稳定、强耦合、非线性的机械系统，可以作为一个典型控制对象被研究，是进行控制理论研究的理想平台，可以用来检验控制方法处理非线性、抗干扰性、稳定性等问题的能力. 倒立摆在军事、工业、生活中都有广泛的运用. 在本系统中，我们运用PID控制器控制旋转倒立摆的起摆，稳摆等动作，进一步检验了PID控制的实用性.

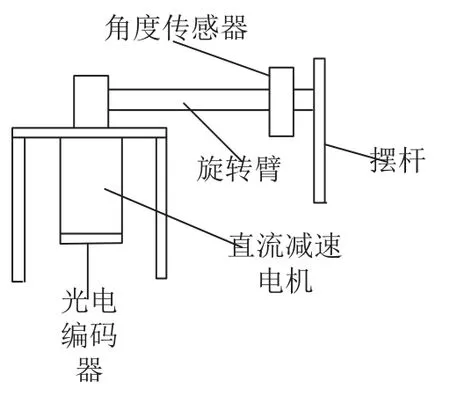
图1 倒立摆运动简图

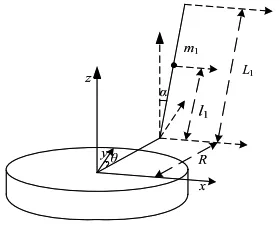
图2 倒立摆系统物理模型

1 倒立摆建模分析

倒立摆的运动结构简图如图1所示，通过对图1的运动简图进行物理建模，得到倒立摆系统的物理模型，如图2所示. 旋转臂的长度为R，旋转臂的质量为m1，水平方向角位移量为θ，摆杆长度为L，重心到杆的长度为l1，竖直方向角位移量为α，摆杆的质量为m2.

其中：T1为旋臂转动动能为摆杆旋转动能T3为摆臂水平方向的动能为摆杆沿竖直方向的动能

在倒立摆运行过程中，α角度非常小，所以sinα≈α≈0，cosα≈1［1］. 将式（1）～（4）各项计算合并，并对其进行线性化处理可得

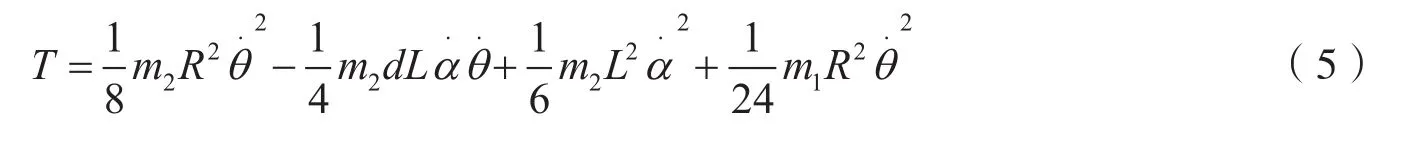
倒立摆的Lagrance方程为

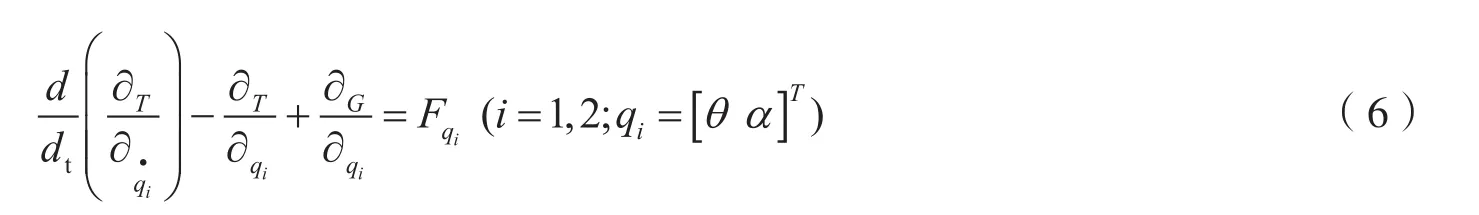
其中，qi为广义坐标，Fqi为作用在系统上的广义力，这里qi表示角度，所以Fqi即为转矩. 同时，我们定义q(t) =[θ(t)α(t) ]T，其中θ(t)为旋臂旋转过零位的角度，α(t)为摆杆旋转过零位的角度.直流电动机的输出转矩则倒立摆系统的Lagrance方程为：

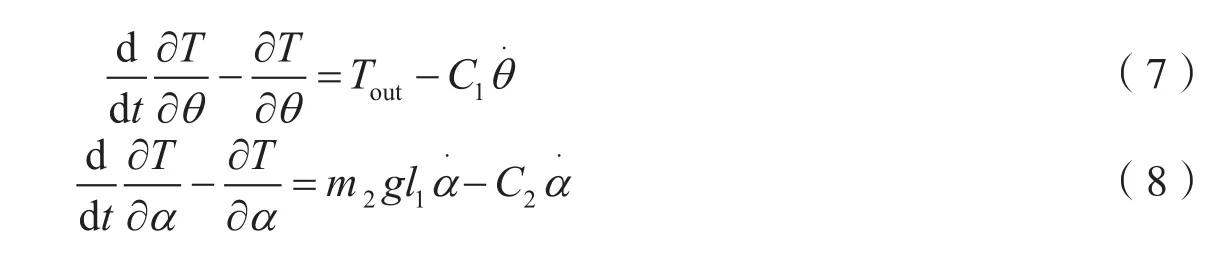
将式（5）代入式（7）可得式（9）

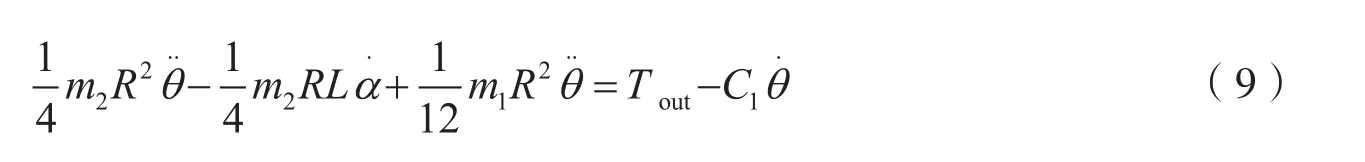
将式（5）代入式（8）可得式（10）

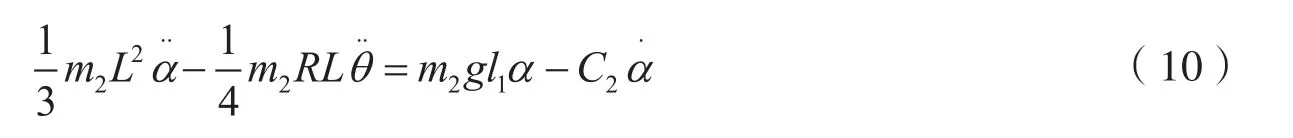
线性化处理后得到的动力学模型可转化为

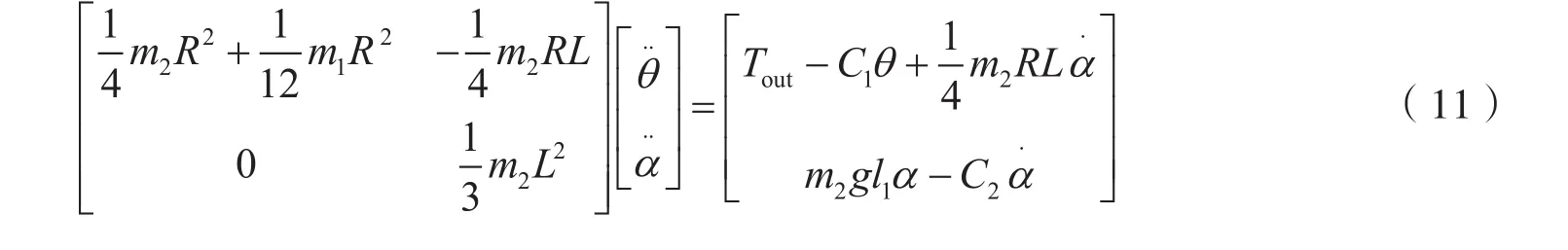
简化矩阵为

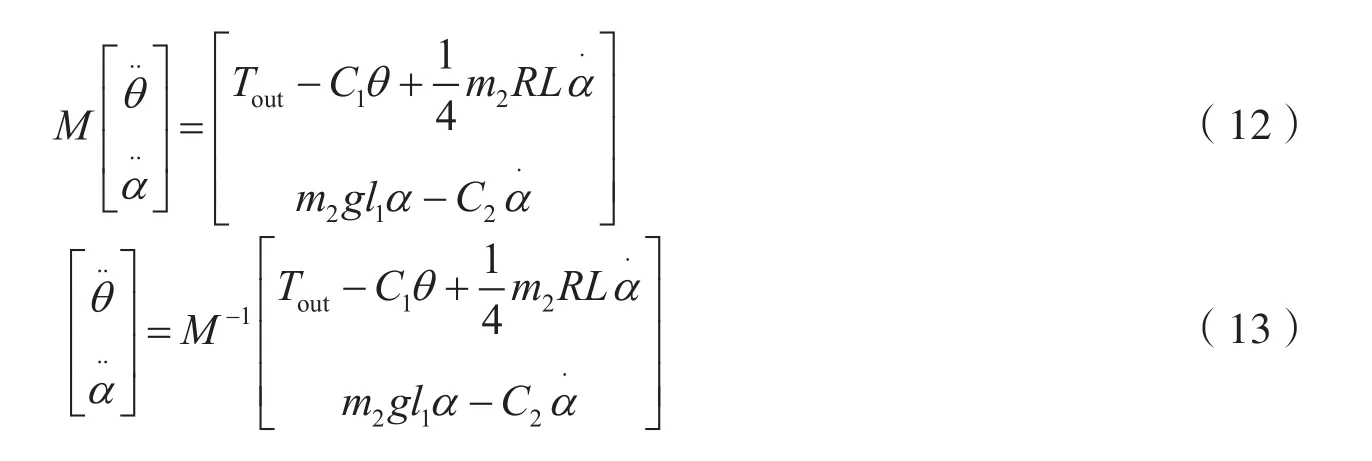
又

将式（14）代入式（13）得到式（15）

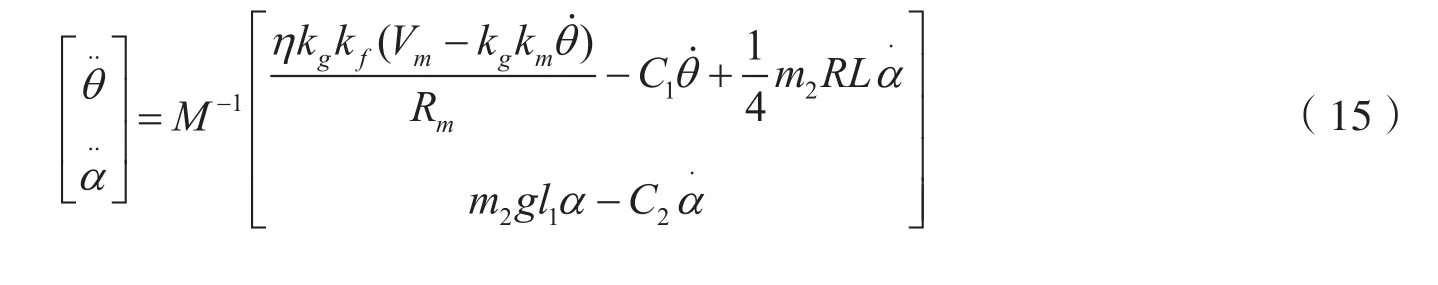
令x则有

将表1中的参数代入上述式中，可以解算出：

2 旋转倒立摆机械硬件设计

表1 状态方程中各参数列表

本系统基于STM32F103微控制器，该芯片资源较为丰富，处理速度较快. 其拥有512 KB的FLASH，我们可以利用它对参数进行整定. 4个通用定时器，我们选用3个定时器，分别给系统提供准确的5 ms定时，读取编码器脉冲数和产生PWM波输出. 利用串口进行代码下载以及与上位机之间数据传输. 利用一个12位ADC对角位移传感器读取数值. 利用外部中断方式实现按键控制.

电机采用原始转速11 000 rpm、减速比30的直流减速电机，直流电机驱动减速器输出动力，将高速扭矩转换为低速扭矩，提供更强大的动力. 硬件驱动为TB6612FNG驱动芯片，并且电机尾部自带有编码器，编码器的齿轮与减速器输出轴的齿轮相啮合，用来检测旋转臂转过的角度.

角度传感器选用WWD35D4，通过STM32的AD转换来读取电阻式角度传感器测量摆杆的旋转角度，并将其作为检测变量送入控制器中，经过PD运算后将角度误差送入PWM信号提供给驱动芯片，驱动直流电机，以带动旋转臂转动，实现倒立摆的起摆和倒立［2］.

本系统选用OLED屏来调节参数，以及观察旋转倒立摆的摆臂运行情况. 通过SPI通信协议与OLED之间实现显示功能. 倒立摆的系统结构图如图3所示.

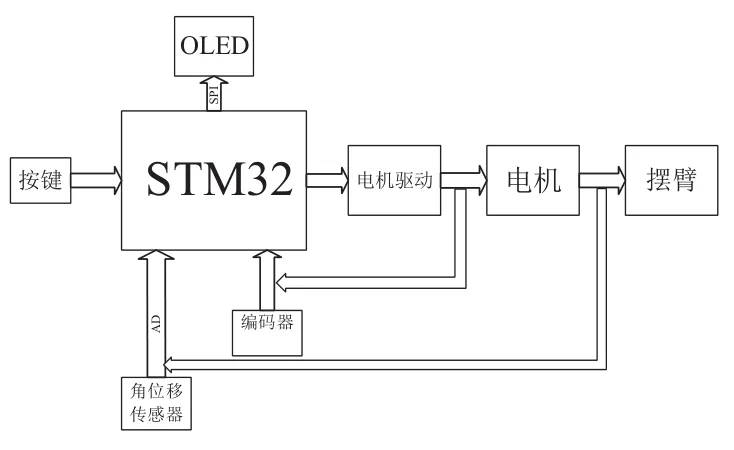
图3 倒立摆系统结构框图

3 旋转倒立摆系统软件设计

本系统软件用STM32F103C8T6作为主控芯片，在系统运行前，在FLASH里面修改与保存PID参数与设定的角位移传感器和编码器标准值. 由按键触发外部中断启动系统运行. 系统利用定时器1中断5 ms的准确工作周期，利用AD读取角度传感器的值来确定悬臂的位置，将角度传感器与标准值的差值通过PID运算后，传给通过定时器2配置成PWM模式驱动的电机，通过定时器3读取编码器值来确定旋转臂的位置，再将编码器与标准值的差值通过PID运算后传给电机. 以此实现双PID闭环控制. 倒立摆软件流程图如图4所示.

3.1 单摆的起摆控制

倒立摆的起摆问题是控制工程中一个比较难解决的经典问题. 根据倒立摆能的数学建模公式可得

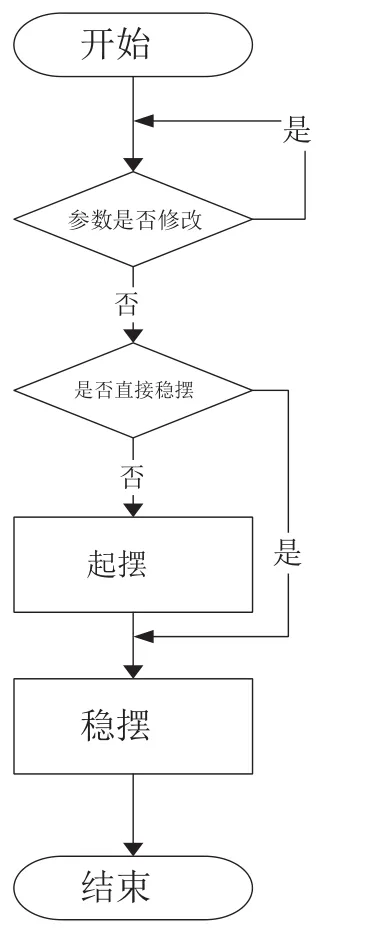
图4 倒立摆软件流程图

可以将倒立摆的起摆问题转化为其摆臂上竖直方向的能量问题. 由式（17）可以将倒立摆的起摆动态过程简化为在这个过程中count_FZ控制摆臂的振幅，在不断震荡的过程中，count_FZ不断增加，直到其摆臂的振幅能够达到稳摆的要求.Count_qb控制的是倒立摆的振荡频率，不断加大震荡的频率以及增加震荡的幅度使倒立摆能够快速达到稳摆的要求.

3.2 倒立摆的稳摆控制

旋转倒立摆的稳摆控制目标是：使倒立摆摆杆稳定在旋转臂正上方的稳定区域，且使α→0，θ→0.

为了实现控制目标，本系统使用了双PID闭环控制系统. 在控制结构中，使用控制器1对倒立摆摆杆的角度α进行控制，控制器的输出极性为正；控制器2对旋转臂的角速度θ进行控制，控制器输出极性为负［3］.

双PID控制系统的结构图如图5所示. 其中的PID控制器（比例-积分-微分控制器）是一个工业控制中常用的反馈控制器，通过被控量与设定值的偏差作为输入信号，而控制器本身就是比例、积分、微分这3个部分的和. 其离散化计算公式为其中kp是比例调节系数，ki是积分调节系数，kd是微分调节系数.PID控制的基础是比例环节；积分控制可消除稳态误差，但可能增加超调量；微分控制可加快惯性系统响应速度以及减弱超调趋势. 本系统采用PD控制即可［1］.

图5 双PID控制结构图

4 系统运行效果

经过对PID参数以及倒立摆平衡中值的反复校正，倒立摆系统能够实现在手动起摆与自动起摆两种运行方式之间顺利切换.

倒立摆在起摆时，利用旋转臂瞬间很大的机械能使摆臂达到倒立条件. 同时利用上位机与下位机的通信获取起摆瞬间的摆臂位置曲线，如图6所示. 图7为倒立摆实际运行图.

5 小结

图6 摆臂的位置曲线

图7 倒立摆稳摆实物图

利用Lagrange方程建立了旋转倒立摆单摆的数学模型，采用正反馈控制角速度使倒立摆迅速振荡，并迅速达到起摆条件. 使用双PID控制方式对倒立摆进行稳摆控制. 由于该系统具有良好的人机交互界面，且设置PID参数较为方便，故适用于实验教学，方便学生直观了解PID控制.