基于投影法的对偶犹豫模糊多属性决策方法及在教育评价中的应用

李兴国

(燕山大学 高等教育发展研究中心，河北 秦皇岛 066004)

现实生活中，模糊性问题大量存在于客观世界，人们所接触到的大量信息多数是模糊和不确定的，致使决策者不能给出精确的评价值。为此，美国学者Zadeh[1]创立了一种描述模糊现象的模糊集理论，应用数学的思维和方法处理模糊性现象。为了解决在实际决策过程中决策者在多个评价值之间的犹豫问题，Torra等[2-3]提出了犹豫模糊集，其元素的隶属函数由一个可能值的集合构成。Zhu和Xu等[4]提出了对偶犹豫模糊集，分别用隶属函数、非隶属函数表达确定性程度和不确定性程度。因为对偶犹豫模糊集更加符合客观事物不确定性的特点，在处理模糊性问题上更具有一般性和灵活性。目前，国内外关于对偶犹豫模糊信息集成算子、距离测度和相似测度的研究成果较为丰富，但是关于对偶犹豫模糊多属性决策方法的研究成果较为缺乏，将投影分析应用于对偶犹豫模糊多属性决策的成果还尚未见到，且尚无学者将对偶犹豫模糊集应用于大学评价体系研究。本文对属性完全未知的对偶犹豫模糊决策问题进行研究，建立基于投影法的对偶犹豫模糊决策模型，将其应用于大学评价体系研究，并基于客观数据和统计学方法进行实证检验。

一、问题描述

本文针对权重完全未知的对偶犹豫模糊集，利用熵值法确定属性权重，建立基于投影分析法的对偶犹豫模糊集排序方法，对备选方案排序择优。设某一多属性决策问题：X={X1，X2，…，Xm}为方案集，C={C1，C2，…，Cn}为属性集，决策者给出方案Xi关于属性Cj的评价矩阵为R=(rij)m×n，其中rij={h(xij)，g(xij)}为对偶犹豫模糊元，表示在属性Cj下对方案Xi的评价分值。属性权重向量w=(w1，w2，…，wn)T完全未知，试建立对偶犹豫模糊多属性决策模型并求解。

(一)对偶犹豫模糊集的距离测度

定义1[5]设A和B是关于集合X={X1，X2，…，Xm}的两个对偶犹豫模糊集，则A和B之间的距离测度为d(A，B)，满足以下条件

①0≤d(A，B)≤1;

②d(A，B)=0当且仅当A=B时成立;

③d(A，B)=d(B，A);

④设C是任意的对偶犹豫模糊集，如果A⊆B⊆C,则d(A，B)≤d(A，C)且d(B，C)≤d(A，C)。

根据上述距离测度定义，对偶犹豫模糊集A和B的标准Euclidean距离测度定义为

(1)

(二)属性权重的确定

应用熵值法确定属性权重，在对对偶模糊集的熵作出定义时，既要充分考虑隶属度和非隶属度，又要体现出决策者在对偶犹豫模糊集中多个数值存在犹豫的特性。

设D={(h1，h2，…，hl1)，(g1，g2，…，gl2)}为一个对偶犹豫模糊值，其隶属度φ(D)、非隶属度φ(D)和犹豫度π(D)指标分别定义如下

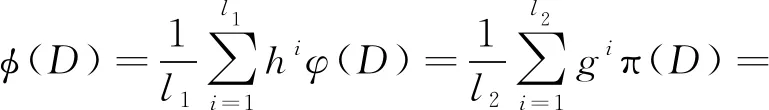
(2)

下面给出对偶犹豫模糊值的熵公理化定义：

定义2 映射E：DHFS(X)→[0，1]称为对偶犹豫模糊集的熵，如果E满足如下条件：

①E(A)=0当且仅当对∀i∈{1，2，…，n}，D={{0}，{1}}或D={{1}，{0}}；

②E(A)=1当且仅当对∀i∈{1，2，…，n}，均有φ(D)=φ(D)；

③E(A)≤E(B)如果对∀xi∈X，当φ(DB(xi))≥φ(DB(xi))时，有φ(DA(xi))≥φ(DB(xi))，φ(DB(xi))≥φ(DA(xi))；或者当φ(DB(xi))≤φ(DB(xi))时，有φ(DA(xi))≤φ(DB(xi))，φ(DB(xi))≤φ(DA(xi))；

④E(A)=E(Ac)。

定义3设A={[xi，DA(xi)]，xi∈X}是论域X上的对偶犹豫模糊集，则

(3)

则E(A)是对偶犹豫模糊集A的熵，证明略。

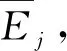
(4)

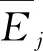
(5)

二、基于投影的对偶犹豫模糊多属性决策模型

(一)模型的构建

设X={x1，x2，…，xm}为决策方案集，C={c1，c2，…，cn}为属性集，属性权重完全未知。决策者对方案xi(i=1，2，…，m)在属性cj(j=1，2，…，n)下的评价信息用对偶犹豫模糊数D={h(x)，g(x)}的形式给出。首先要对偶犹豫模糊值进行规范化处理，处理方法如下：

设D=(h(x)，g(x))为对偶犹豫模糊数，在集合h(x)和g(x)两个集合中，元素次序通常是紊乱的，需对两集合中的元素重新进行排序。令σ：(1，2，…，m)→(1，2，…，m)为一个排列，使得hσ(s)≥hσ(s+1)，其中s=1，2，…，m-1，令δ：(1，2，…，n)→(1，2，…，n)为一个排列，使得gδ(t)≥gδ(t+1),其中t=1，2，…，n-1。

此外，在不同的对偶犹豫模糊数D=(hD(x)，gD(x))和F=(hF(x)，gF(x))中，集合hD(x)与hF(x)中及集合gD(x)与gF(x)中所包含元素个数可能会有所不同，令l=max{l(hD(x))，l(hF(x))}、k=max{k(gD(x))，k(gF(x))}。其中，l(hd(x))、l(hF(x))、k(gD(x))、k(gF(x))分别表示hD(x)、hF(x)、gD(x)、gF(x)中元素的个数。在乐观准则下，向集合中添加最大的元素，在悲观准则下，向集合中添加最小的元素，使得l(hD(x))=l(hF(x))，k(gD(x))=k(gF(x))。

定义5D=(h(x)，g(x))为对偶犹豫模糊数，其中h(x)={hσ(1)(x)，hσ(2)(x)，…，hσ(l)(x)}、g(x)={gδ(1)(x)，gδ(2)(x)，…，gδ(k)(x)}，则D的信息能量为

(6)

则A的模可定义为

(7)

定义6设D=(hD(x)，gD(x))和F=(hF(x)，gF(x))为两个对偶犹豫模糊数，其中hD(x)={hDσ(1)(x)，hDσ(2)(x)，…，hDσ(l)(x)}、gD(x)={gDδ(1)(x)，gDδ(2)(x)，…，gDδ(k)(x)}、hF(x)={hFσ(1)(x)，hFσ(2)(x)，…，hFσ(l)(x)}、gF(x)={gFδ(1)(x)，gFδ(2)(x)，…，gFδ(k)(x)}，则D与F的相关性指标定义如下

(8)

定义7 设D和F为两个对偶犹豫模糊数，则有D与F的相关系数，即夹角余弦可定义为

(9)

结合定义6和定义7，给出对偶犹豫模糊数投影定义如下：

定义8 设D和F为两个对偶犹豫模糊数，则D在F上的投影定义为

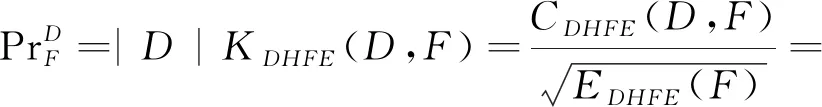
(10)

定义9 令D*(xi)=(h*(xi),g*(xi))为理想对偶犹豫模糊数，其中

(11)

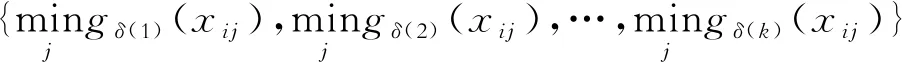
(12)

则对偶犹豫模糊数D在理想对偶犹豫模糊数D*上的投影为

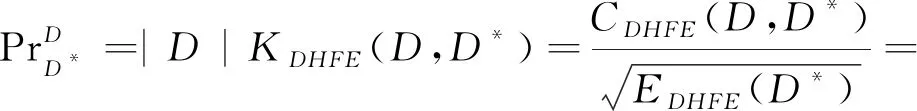
(13)

对各对偶犹豫模糊元投影的加权求和，得各方案的综合评价分值

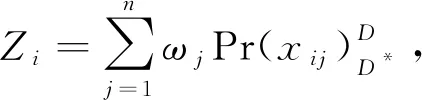
(i=1,2,…,m;j=1,2,…,n)

(14)

根据Zi值的大小，对各方案Xi进行排序择优。

(二)模型决策程序

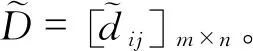
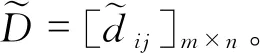
Step3:依据式(11)和(12)，得理想对偶犹豫模糊元D*(xi)=(h*(xi)，g*(xi))。

Step4：依据式(13)，计算对偶犹豫模糊数D在理想对偶犹豫模糊数D*上的投影矩阵α=[αij]m×n。

Step5：依据式(3)、(4)和(5)，计算各属性Cj的权重。

Step6：依据式(14)，计算各方案的综合评价分值Zi。

Step7：根据Zi的大小，对各方案排序择优。

三、实例分析

(一)案例描述

大学排名自出现以来，就引起了社会各界的广泛关注。1987 年9月，中国管理科学研究院以《科学引文索引》(SCI)为指标对我国87 所重点大学进行了排名，排名结果发表在《科技日报》上，这个大学排名是我国第一个严格意义的大学社会评价，具有划时代的意义[6]。目前，国内知名度和影响力较大的大学排行榜主要有3个：中国管理科学研究院发布的武书连中国大学排名(以下简称“中管院榜”)、艾瑞深中国校友会网发布的中国大学排名(以下简称“校友会榜”)、武汉大学中国科学评价研究中心发布的中国大学排名(以下简称“中评榜”)。这3个中国大学评价体系的3级指标都包含教师人数、毕业生人数等反映办学规模的指标。那么，这3个大学评价体系下大学评价得分与高校的办学规模是否存在显著的相关性，如果存在，哪个中国大学评价体系的相关性最强? 以上即本文要探讨的问题[7]。

(二)建立模型及求解

如果在某个大学评价体系下，一所高校的规模越大(用教师和学生人数衡量)，其排名越靠前，则称该大学评价体系具有规模效应。大学评价体系的规模效应越强，其排名结果越有利于规模较大的综合性高校，不利于特色型和专业型高校。中管院榜、校友会榜和中评榜是国内最知名的3个大学评价体系，其3级评价指标均包含专任教师和毕业学生人数。为研究3个中国大学评价体系是否具有规模效应及相对强度，应用对偶犹豫模糊决策方法进行检验。

构造模型如下：方案集A={A1，A2，A3}：A1为中管院榜，A2为校友会榜，A3为中评榜；属性集C={C1，C2，C3，C4}：C1为专任教师数，C2为本科毕业生数，C3为硕士毕业生数，C4为博士毕业生数。请专家对其进行评价，受认知思维模糊性的影响，专家给出的是对偶犹豫模糊评价信息。基于评价信息建立对偶犹豫模糊决策矩阵，见表1。

表1 原始的对偶犹豫模糊决策矩阵DA

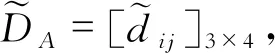
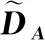
表2 规范化的对偶犹豫模糊决策矩阵

其次，根据公式(11)和(12)，得到理想对偶犹豫模糊元D*(xi)，分别为：({0.8,0.6},{0.2,0.1,0.1})、({0.7,0.6},{0.2,0.2})、({0.9,0.7,0.6},{0.1,0.1})、({0.8,0.7},{0.2,0.1})。

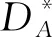
然后，根据熵值法，计算属性集C的权重向量w=(w1,w2,w3,w4)T，得到：w1=0.289 4,w2=0.145 6,w3=0.252 8,w4=0.312 2。

最后，根据公式(14)，计算各方案的综合评价分值Zi：Z1=0.617 6，Z2=0.492 8，Z3=0.716 4 决策结果：因为Z3>Z1>Z2，所以A3>A1>A2。即中评榜的规模效应最强，其次为中管院榜，校友会榜的规模效应最弱。

四、实证检验

(一)研究数据的选取

为了验证上节的结果，运用统计学中的相关分析法，基于2013年中管院排行榜、校友会排行榜和中评榜下“985高校”“211高校”和“100强高校”的排名数据，对各大学排行榜的排名数据进行实证检验。分别计算在3个不同的中国大学评价体系下，一所大学的总得分与本科毕业生数、硕士毕业生数、博士毕业生数和专任教师数等4项指标的相关系数，结果分别见表3、表4和表5。

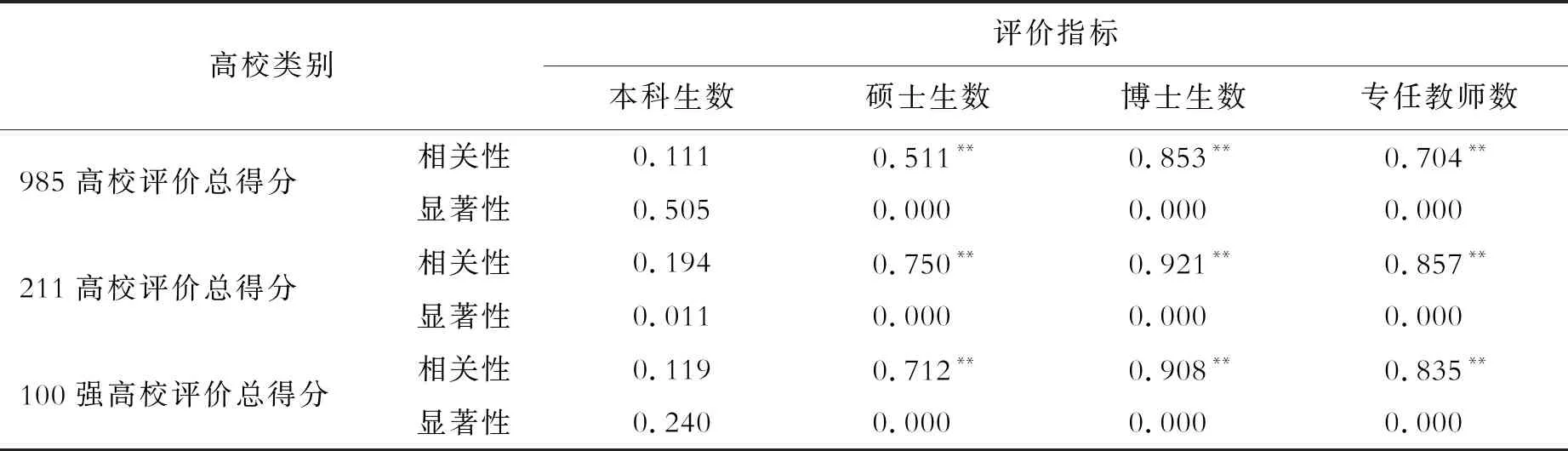
表3 中管院榜大学评价总得分与高校规模的相关分析

注：**表示在0.01的水平上显著相关。

表4 校友会榜大学评价总得分与高校规模的相关分析

注：**表示在0.01的水平上显著相关。

表5 中评榜大学评价总得分与高校规模的相关分析

注：**表示在0.01的水平上显著相关。

(二)实证分析结论

在中管院、校友会、中评榜3个不同的中国大学评价体系下，本科生培养得分与本科生人数之间并不存在显著的相关性，表明在统计学意义上没有充分证据表明本科生规模对本科培养得分和大学评价总分有显著影响。

研究生培养得分与研究生数存在显著的正相关，在3个中国大学评价体系下的大学评价总分与硕士生人数的相关系数为0.506～0.779，大学评价总分与博士生人数的相关系数为0.821～0.927之间，且均在0.01的水平上显著。并且博士生数与研究生培养得分的相关系数大于硕士生，说明研究生规模对研究生培养得分、大学评价总分均具有显著影响。

中评榜办学规模对大学评价的影响效应最强，中管院榜居中，校友会榜最弱。且办学规模影响效应与高校办学层次成反比。“211高校”办学规模影响效应最强，其次是“100强”高校，“985高校”办学规模影响效应最低。表明高校综合实力越强，办学规模对大学评价得分影响越弱。统计检验结果与模糊多属性决策模型所得分析结果一致，从而证明了本文所建模型的有效性。

五、结语

本文主要构建了基于投影分析法和熵权法的对偶犹豫模糊多属性决策模型，并应用该模型对3个不同的中国大学评价体系下高校办学规模影响效应进行了分析。为验证模型的有效性，运用统计学中的相关分析法，基于2013年中国大学评价的事实数据，对3个不同的中国大学评价体系的办学规模效应进行实证检验，所得结论与模型研究结论一致，从而证明了本文所建决策模型的有效性。