一种新的IMU/GPS组合导航抗差渐消滤波算法

项 鑫

(河南省煤田地质局物探测量队，郑州 450009)

0 引言

当前，利用多种导航技术集成来改善导航设备的性能已成为导航定位发展的一个重要方向。GPS具有精度高、全天候观测等特点，INS无需接收和发送信号，稳定性较好，二者组合形成的导航系统已得到广泛研究及应用。Kalman滤波是多源数据融合的常用方法，已广泛应用于动态导航定位领域。Kalman滤波的性能取决于系统模型及噪声特性假设的精确程度。当模型存在较大误差时，Kalman滤波结果常常会发散[1]。为抑制Kalman滤波器的发散，文献[2]中给出了一种基于衰减记忆思想的最优渐消滤波算法。但该算法采用一个渐消因子对多维系统状态进行自适应调整，难以确切描述系统状态的变化，难以保证整个滤波器的绝对最优。在单个渐消因子滤波的基础上，研究人员又提出了次优渐消滤波[3]、多因子渐消滤波[4]等方法。理论上，渐消滤波具有控制状态模型误差影响的能力，但上述渐消滤波方法对异常观测值的鲁棒性不高，而异常观测值将有可能导致滤波结果的发散。无穷范数滤波能够使估计误差的能量经过量测误差和初始误差归一化之后达到最小[5,6]，并且能够处理系统模型和噪声的不确定干扰问题，已应用于GPS/INS组合导航系统中[7-9]。但无穷范数滤波算法无法抵抗粗差的影响，遇到粗差往往导致滤波结果的发散[10]。作为抵抗异常值影响的一种实用方法[11,12]，抗差估计着力于估值的实际抗差性和可靠性。因此，可引入抗差估计方法来抵抗异常值的影响。基于此，本文提出了一种新的多重渐消抗差滤波算法，利用实际环境下的GPS/INS组合导航设备进行了数据采集，用提出的滤波算法进行解算，并与其他多种滤波算法进行了对比分析，验证了所提滤波算法的有效性。

1 渐消滤波与H滤波

1.1 渐消滤波

对于动态模型状态方程和观测方程

(1)

其中，xk为k历元的状态向量，Φk/k-1为状态转移矩阵,Hk为观测矩阵,zk为观测向量，wk和vk分别为系统噪声和观测噪声，其渐消滤波解为

(2)

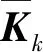
Sk为渐消因子且Sk≥1，Pk-1为k-1历元状态向量的协方差矩阵，Rk和Qk分别为观测噪声和状态噪声的协方差矩阵。显然，在渐消滤波中，先验状态估计的协方差矩阵被放大了Sk倍，这将有效降低过去信息的影响力。与标准Kalman滤波相比，渐消滤波很好地控制了上一历元的状态误差影响。

渐消滤波的关键是选择合适的渐消因子。由于单个渐消因子很难保证滤波的最优性，故提出了一种多重渐消因子[3]，即：

Sk=diag(s1,s2,…,sm,1,…,1,…,1),

(4)

(i=1,2,…,m),

(5)

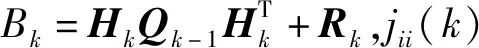
1.2 无穷范数滤波

对于非线性系统

(6)

其中，f(·)和h(·)分别为非线性状态转移函数和非线性观测矩阵，xk为待估计的状态向量，定义代价函数为[13]

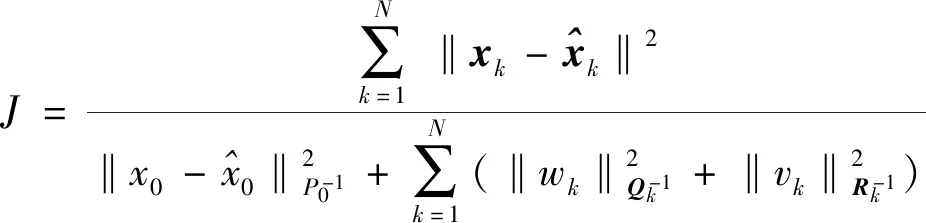
(7)

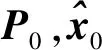
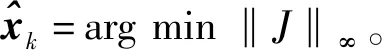
(8)

其中，Pk是xk的协方差矩阵,Lk在本文中为单位矩阵。在非线性无穷范数滤波中，Pk/k的迭代公式为:

(9)

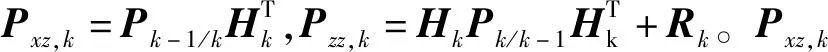
值得注意的是，γ的值与滤波的抗差性能密切相关，γ减小则滤波器的抗差性能提高。然而，γ太小则可能导致滤波的发散。因此，一个合适的γ值通常根据实际经验来设定。

2 一种新的抗差渐消滤波算法

为提高滤波器的灵活性及滤波性能，提出了一种多重渐消因子[3]，但这种滤波方法的抗差性仍可进一步改善。因此，本文提出了一种改进的抗差渐消滤波算法来进一步改善渐消滤波的抗差性能。在多重渐消滤波中，渐消因子为Sk=diag(s1,…,sm,1,…,1)，其中m为xk中可观测元素的总数。在此将Pk/k-1表示为Pk/k-1=SkΦk,k-1Pk-1ΦTk,k-1Sk+Qk以保证其对称性。

针对滤波中的异常观测值，引入抗差估计方法以改善滤波器的抗差性能。预测状态向量中的各分量一般是相关的，因此引入双因子λij构造的等价协方差矩阵，即

(11)

(12)

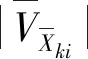
(13)

由此，可以构造出一种新的抗差多重渐消无穷范数滤波算法。

3 GPS/INS组合导航系统

在GPS/INS组合导航系统中，松散组合方式计算简便、易于实现，得到了广泛应用。在GPS/INS松散组合导航系统中，设计了一个15维度的状态向量，即

(14)

向量中的各元素分别为位置、速度、姿态的偏差值以及陀螺仪和加速度计的噪声值。

在GPS/INS松散组合导航系统中，状态方程的离散化形式为[1]：

Xk=Φk,k-1Xk-1+Wk,

(15)

其中，Xk为状态向量，Wk为动力模型误差向量，Φk,k-1为离散后的状态转移矩阵，以GPS与INS系统的位置与速度输出作为外部量测：

Zρ(t)=ρGPS-ρINS

(16)

其中，rGPS和vGPS为GPS的输出信息，rINS和vINS为INS的输出信息。量测方程为：

(17)

4 实验与分析

本文的实验数据由车载GPS/INS组合导航系统采集得到，实验利用两台天宝GPS接收机和一台低成本的惯性测量设备。GPS坐标数据由双差伪距计算得到，以双差载波相位结算结果作为参考解。为进一步检验各种算法的稳定性及抗差性，设计了两组方案以验证新算法的稳定性及抗差性能，每组方案均采用四种滤波算法进行解算，在无穷范数滤波中，γ均设为2。这四种方案分别为：

方案一：Kalman滤波；

方案二：无穷范数滤波；

方案三：多重渐消无穷范数滤波；

方案四：抗差多重渐消滤波。

每个方案均用自行设计的组合导航数据处理程序进行了解算，在这个算例中，人为地在GPS观测值中的部分历元加入了粗差。得到各方案的解算结果如图1到图4所示。

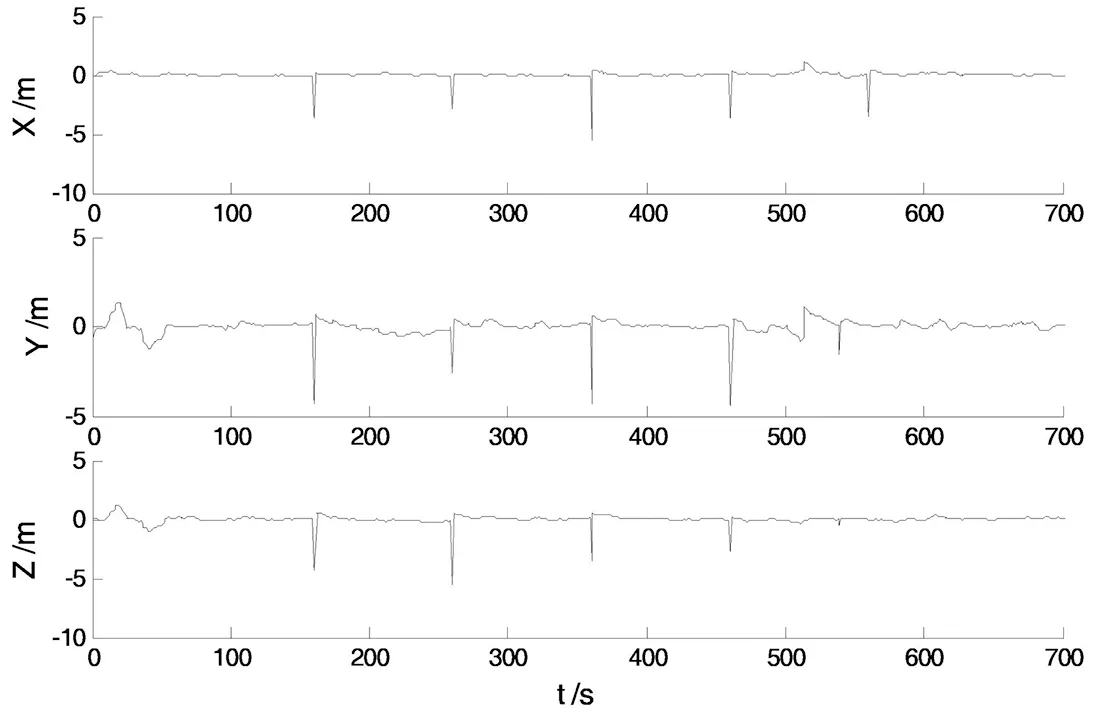
图1 方案一的位置误差

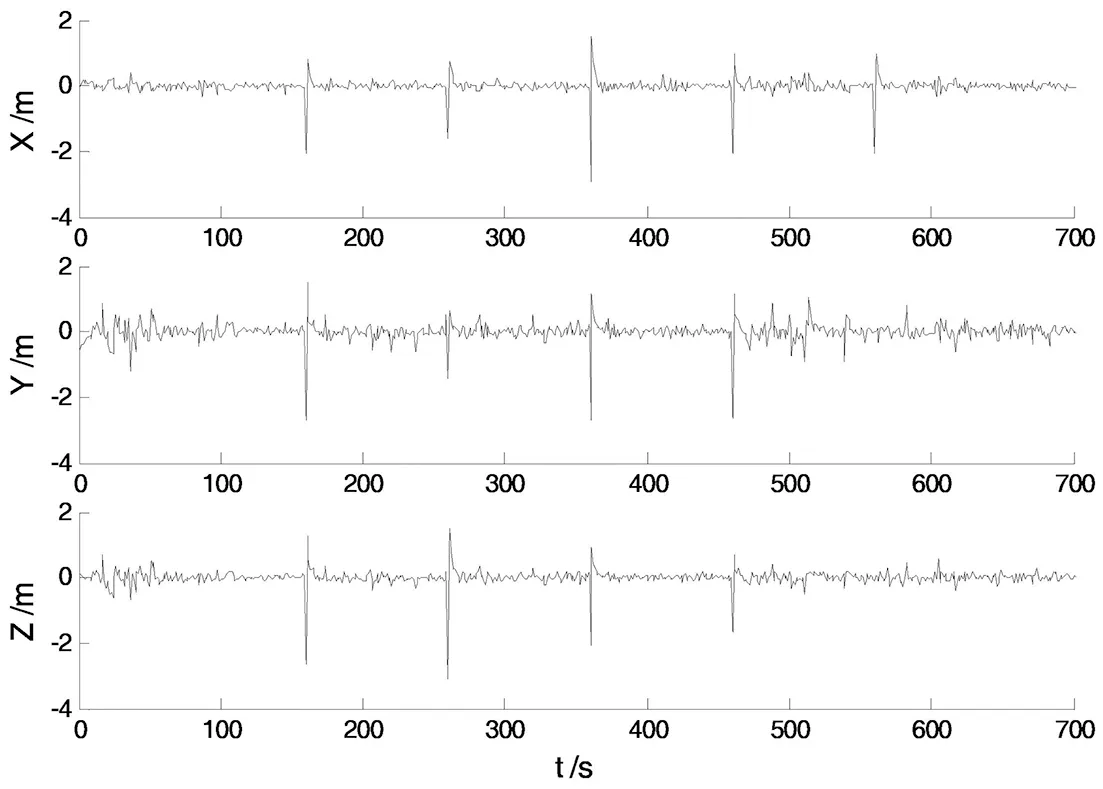
图2 方案二的位置误差

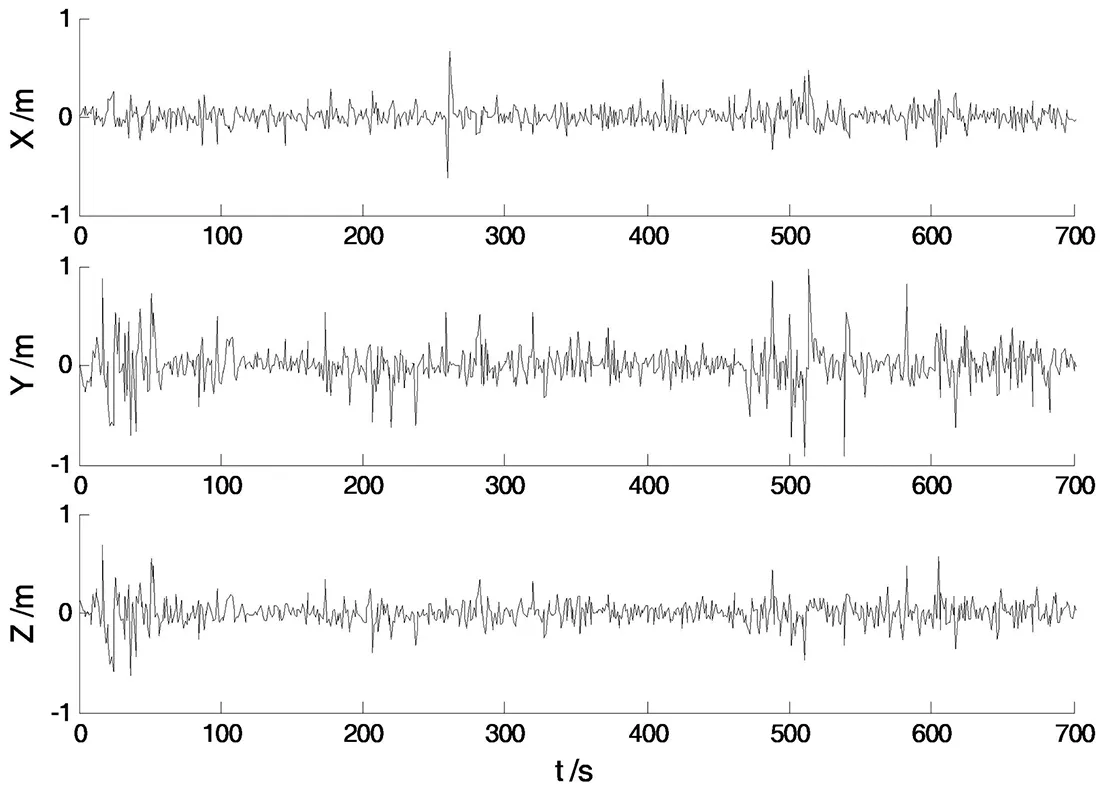
图3 方案三的位置误差

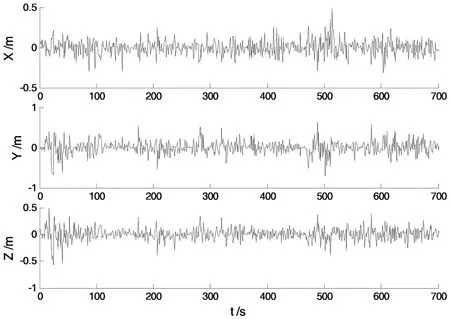
图4 方案四的位置误差

该实验中，由于初始观测值中包含粗差，故各方案的解算结果主要受粗差影响。从图1、2可以明显看出，方案一和方案二算法的抗差性能较差。而图3、4则表明方案三算法及方案四算法均表现出了较好的抗差性。此外，本文提出的改进的多重渐消滤波算法误差振幅最小，具有更高的解算精度。各方案的RMSE值如表1所示：

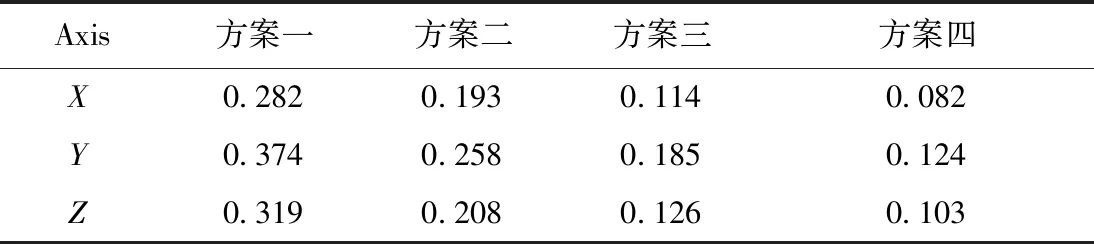
表1 各方案的RMSE值

由于受到粗差的强烈影响，方案一和方案二算法的解算结果较差，各方向的RMSE值均较大。而方案三及方案四算法的RMSE值则变化较小，这说明二者均能较好地抵抗粗差的影响。由于动态模型误差及不确定误差的影响均被控制在一定的范围内，本文提出的改进方法解算效果优于其他几种方案。

5 结论

本文提出的多重渐消滤波算法，结合了多重渐消滤波与无穷范数滤波的优点。利用真实环境下采集的IMU/GPS组合导航数据对改进的滤波算法性能进行验证，得出如下结论。

①异常观测值能够对Kalman滤波与无穷范数滤波的解算结果产生较大干扰， 而多重渐消滤波则对异常值有一定的抵抗性；

②本文提出的多重渐消滤波算法能够应用于松散组合的IMU/GPS组合导航系统中，在有无粗差的情况下均表现出了较好的稳定性及抗差性。