黄河近百年径流演变特征分析

胡慧杰，崔 凯，曹 茜，李姝蕾，常肖杰，沈丽娜

（1.河南黄河水文勘测设计院，河南郑州450004；2.黄河勘测规划设计研究院有限公司，河南郑州450003；3.河南省许昌水文水资源勘测局，河南许昌461000）

受气候变化的影响和人类活动的干预,流域水循环规律逐渐发生变化,径流演变规律也随之改变。河川径流量是流域水资源科学开发利用、合理调度配置的基础［1］,因此研究径流演变特性对流域水资源的高效利用、合理规划具有重要意义。

黄河是我国的第二大河,承担着流域供水、灌溉、防洪、防凌、生态等多方面任务。黄河水情的不利形势将对沿黄地区的工农业生产、生态环境造成极大影响,研究黄河径流的演变过程,分析其演化特性,有助于深刻认识水资源变化规律,科学控制水资源开发利用过程。近几年很多学者对上游唐乃亥站径流有较深入研究［2］,而对黄河下游花园口水文站径流研究不多。花园口水文站是国家级水文站,地处黄河中下游的节点部位［3］,发挥着为黄河下游防洪调度与水资源管理提供重要水文信息的作用。花园口水文站以上的汇流面积占黄河流域总面积的97%,来水量占黄河总水量的96.6%,因此花园口水文站来水量大小基本反映黄河水量的丰、枯状况,分析花园口水文站近百年（1919—2016年)的径流演变可以反映黄河流域的径流演变特性,从而为黄河水资源配置调度及管理规划提供重要的参考依据。

1 数据来源

花园口水文站1938年建站,1949年1月起有连续的观测资料,建站之前的径流数据根据陕县站1919年以来的径流量插补延长［4］,最终得到花园口水文站1919—2016年各水文年（7月至次年6月)的天然径流量。本文采用经过还原的天然径流时间序列分析黄河径流的演变规律。

2 数据分析

径流时间序列是水文时间序列的一种,一般包含确定成分和随机成分。为深刻反映黄河流域径流变化规律,本文运用水文时间序列分析方法,对径流数据的突变点及突变前后的趋势性进行分析。

2.1 统计特征分析

水文学常用的统计特征值包括平均值、极值、极差、均方差、变差系数、偏态系数、年际极值比等［5］。其中,变差系数和极值比反映的是径流的相对变化程度,这两个特征值越大表明径流的年际变化越剧烈,径流资源的利用难度越大,对水资源管理的要求越高［6］,反之,则表示径流的年际变化较为平缓,有利于水资源的开发利用。

花园口1919—2016年各水文年度的径流量变化见图1,其中：1964—1965年度的天然径流量最大,为938.7亿m3；2002—2003年度的天然径流量最小,为257.4亿m3。径流量最大值为最小值的3倍多,极差为681.3亿m3,说明黄河来水年际间相差较大。

图1 花园口水文站年天然径流量变化过程

1919—2016年多年平均径流量为532.5亿m3,标准差为135.4亿m3,变差系数为0.25。第一个黄河流域规划于1955年通过,此后开展了黄土高原水土流失治理,建设了一大批淤地坝；流域第一座大型年调节水库龙羊峡水库1986年建成并投入使用；1999年开始实施全河统一水量调度。按以上重要年份将径流时间序列分为不同的时段,各时段的特征值见表1。其中,1956—2016年的标准差较大,其序列值较为分散,即1956年以来径流量年际变化较为剧烈,径流资源的利用难度较大。

1956—1986年径流量平均值为606.1亿m3,变差系数为0.23,相对1956—2016年的变化较为集中。1987—2016年径流量均值为450.6亿m3,变差系数为0.20,偏态系数、极差相对1956—1986年均较小。可见,1987年以来黄河径流相对集中,极差为373.0亿m3,而1999年以来黄河来水较少并出现负偏现象。

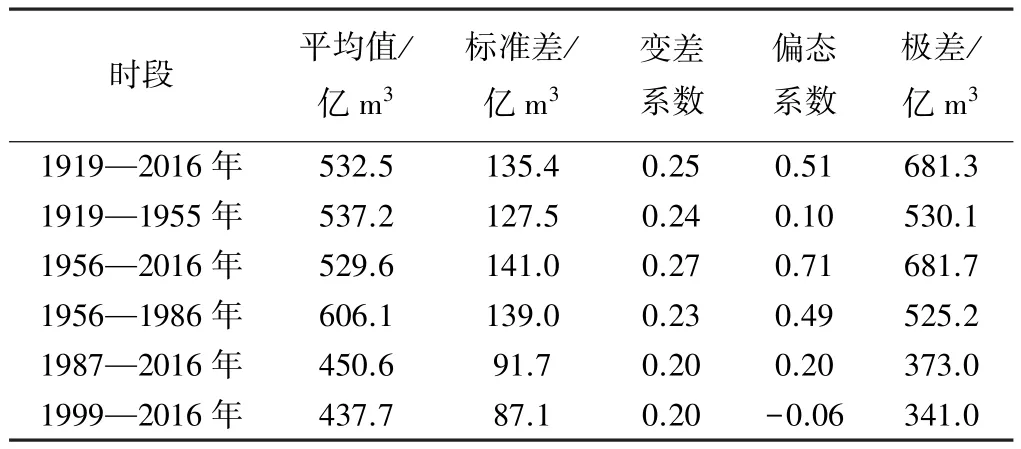
表1 各时段径流时间序列特征值

从特征值分布来看,1956—1986年径流量平均值最大,1999—2016年径流量平均值最小,表明1956—1986年黄河来水相对较多。1999—2016年径流量标准差及变差系数最小,其次是1987—2016年,即近30 a的黄河来水变化相对较为平缓。1956—2016年径流量偏态系数最大,正偏幅度最大；各时段中只有1999—2016年偏态系数为负,出现负偏。1919—2016年与1956—2016年两时段的极差最大,极差最小的时段为 1999—2016年,其次为1987—2016年,可见近30 a黄河流域的来水变化幅度相对较小。

2.2 突变分析

突变分析即对数据序列的变异进行诊断,突变主要包括均值突变、方差突变、趋势突变、概率突变、谱突变、模型参数突变等几种类型［7］。水文时间序列的突变主要指均值突变或趋势突变,即时间序列从一个均值状态或者趋势突然跳跃到另一个均值状态或趋势的突变［8］。突变分析常用的方法主要包括有序聚类分析法、Mann-Kendall突变检验法、滑动t检验法等。

2.2.1 有序聚类分析法

有序聚类分析法是通过统计分析提取序列突变点的有效方法,主要思想是利用离差平方和判断突变点,认为同类之间的离差平方和最小,而类与类之间的离差平方和最大［9］。采用该方法可以分析水文时间序列中径流量或降水量的突变点。

设有水文时间序列xt（x1,x2,…,xk-1),突变点为τ,则突变前后的离差平方和分别为

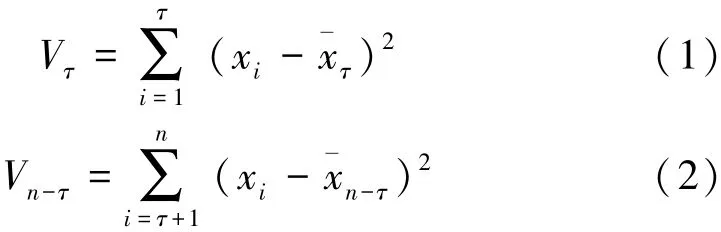
式中：¯xτ、¯xn-τ分别为τ前后两部分的均值。

总离差平方和为

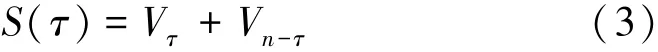
取S（τ) 的极小值,则当S＝minSn（τ) （2≤τ≤n-1)时,分割点两侧的离差平方和最小,即τ为最优二分割（突变点)。

运用有序聚类分析法对花园口水文站的年径流量时间序列进行突变点分析,计算与τ对应的Sn（τ),点绘Sn（τ)变化曲线（见图 2)。 由图 2可知,Sn（τ)最小值出现在1990—1991年度,该年度为最可能的突变点。1933—1934年度Sn（τ)局部最小,故该年度也可能是突变点。因此,花园口水文站年径流量可能在1990—1991年、1933—1934年发生了突变。

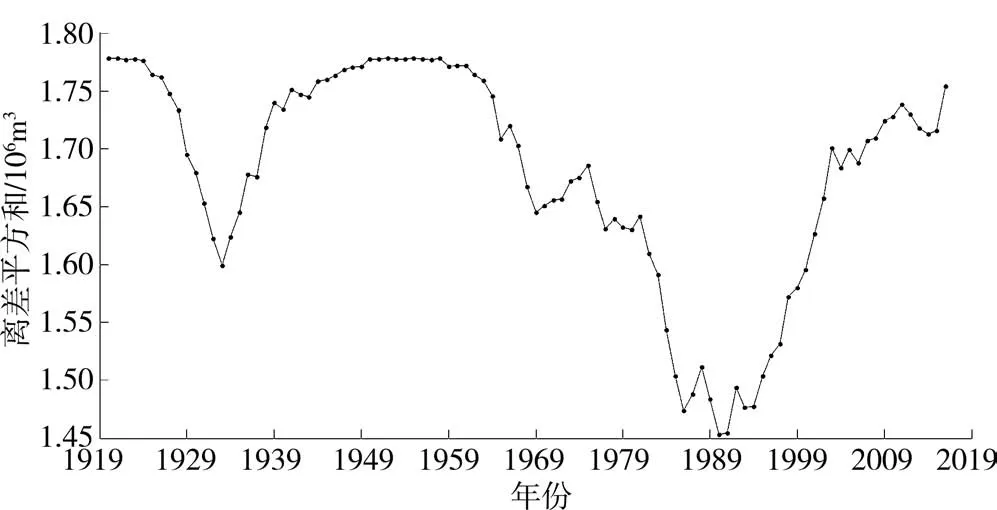
图2 花园口水文站年径流有序聚类S变化曲线

2.2.2 Mann-Kendall突变检验法

Mann-Kendall突变检验法广泛应用于非参数检验,是时间序列分析常用方法之一［10］。该方法由Mann和Kendall于1954年提出,近年来被广泛应用于分析径流、气温、降水和水质等要素时间序列的突变情况。Mann-Kendall突变检验法不要求被分析样本遵从一定分布,也不受其他异常值的干扰,适用于气象、水文等非正态分布数据,计算十分简便。应用Mann-Kendall突变检验法进行序列突变检验时,对时间序列xt（t＝1,2,…,n),构造一秩序列［11］：

其中

定义统计量：

其中

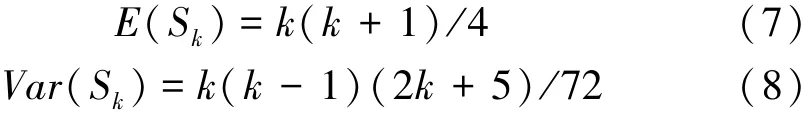
式中：E（Sk)和Var（Sk)分别为累计数Sk的均值和方差。

将时间序列xt（t＝1,2,…,n)按降序排列,再按式（8)计算,同时使

当k＝1时,UF1为0,服从标准正态分布。

运用Mann-Kendall突变检验法检验时间序列的突变性时,将UFk和UBk两条统计量序列曲线和显著性水平为0.05的正态分布值U0.05＝±1.96两条临界线绘制在同一张图上。如果UFk和UBk两条曲线在两条临界线U0.05＝±1.96之间相交,则说明该序列有突变,交点对应的时刻便是突变开始的时间。按照上述方法,得出花园口水文站年径流量在1922—1923年度、1993—1994年度可能发生了突变（见图3)。

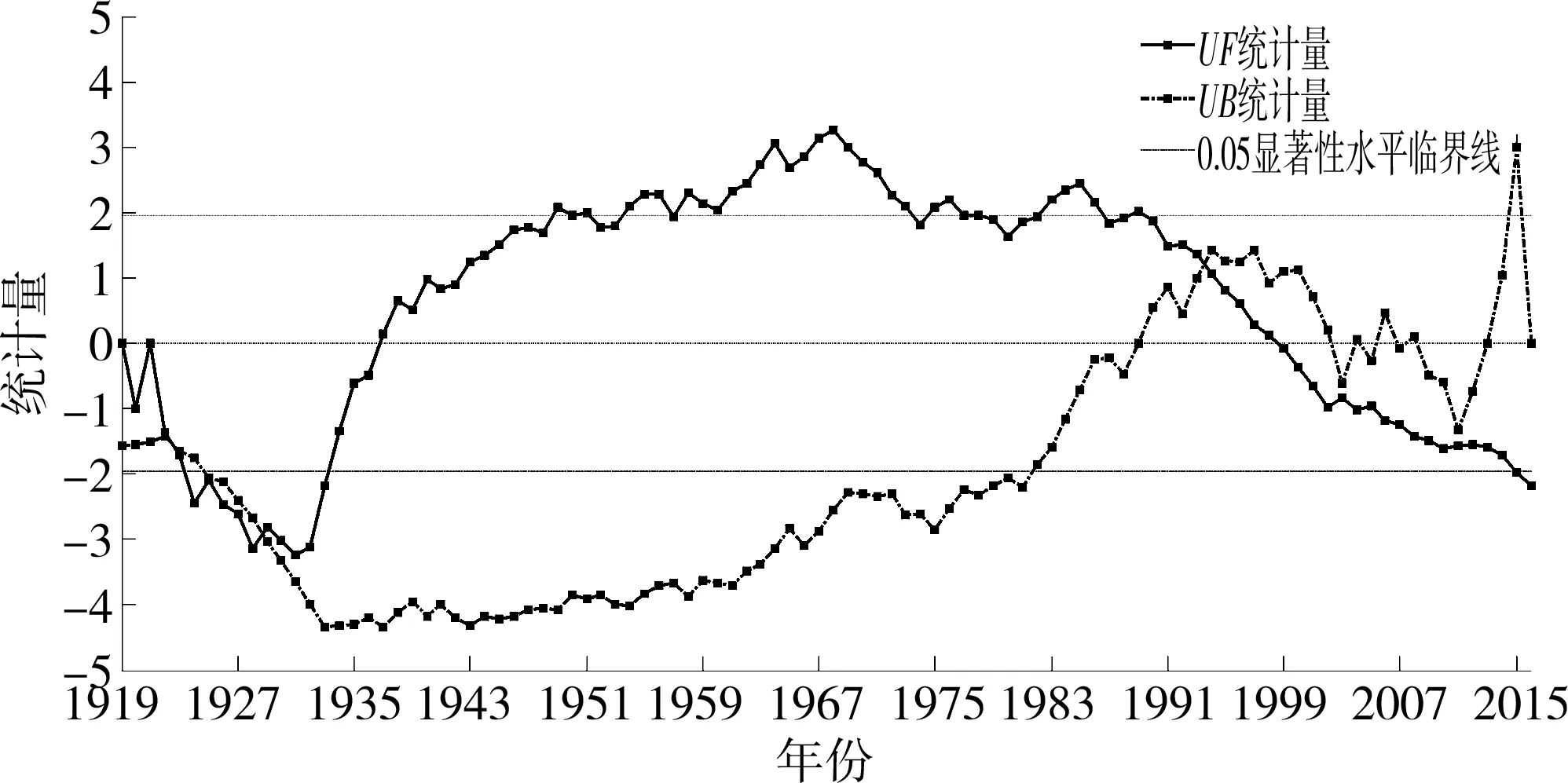
图3 花园口水文站年径流量Mann-Kendall突变检验曲线

2.2.3 滑动t检验法

滑动t检验法是根据检验样本均值存在的差异是否显著的方法来检验突变的,其基本思想是把时间序列中两段子序列的均值是否存在显著差异,看成来自总体的均值有无显著差异来进行检验。如果两段子序列的均值之间的差异超过了一定的显著性水平,就可认为有突变发生。

设滑动点前后两个序列总体的分布函数分别为F1（x)和F2（x),从中分别抽取容量为n1和n2的两个样本,检验原假设,若F1（x)＝ F2（x),则该抽样分布函数为

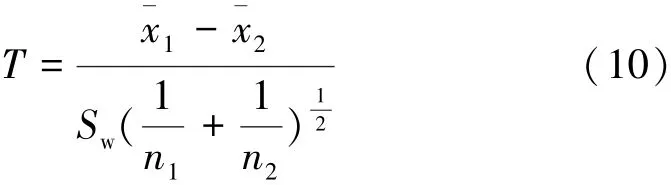
其中

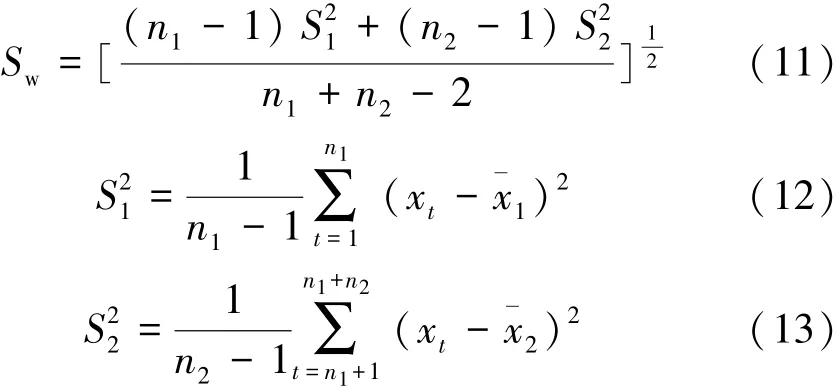
式中：¯x1、¯x2分别为前后两个样本的均值；、分别为两个样本的方差；Sw为两个样本方差的线性组合。

T服从t（n1+n2-2)分布,与显著性水平 α＝0.05时在 t分布表中查得的临界值 t1-α／2对比,若 ｜T ｜＞t1-α／2,拒绝原假设,则两子序列存在显著性差异；反之,两子序列不存在显著性差异［12］。本文子序列长度n1和n2取8,选取α＝0.01显著性水平检验变异程度。运用滑动t检验法对花园口水文站的年径流量进行突变分析,检验样本均值存在的差异是否显著,结果见图4。由图4可知,花园口水文站年径流量在1929—1939年、1968年、1985年、1988—1991年、2002年发生变异,其中1930—1934年、1989—1991年为0.10显著性水平下的变异点。

2.2.4 突变点检验结果及成因分析

对以上3种检验法得到的突变点进行汇总,见表2。

表2 年径流量突变点检验结果

由表2可以看出,花园口水文站年径流量在水文年1933—1934年度、1989—1990年度发生了突变。因此,将花园口的径流时间序列分为1919—1933年、1934—1989年、1990—2016年3个阶段。

径流形成过程是多重因素相互作用的复杂自然现象。资料显示,黄河流域1933年发生特大洪水,受灾面积超过1万km2,而1972—1989年黄河连年断流。20世纪30年代,流域用水规模不大,自然因素起主导作用,1933年突变的主要因素为全球大尺度的降水、气温变化；80—90年代用水量激增,流域尺度的小循环使得径流时间序列发生突变,1989年的突变现象主要为人为因素导致的用水量增加和流域下垫面改变。

2.3 趋势分析

趋势分析即分析水文时间序列变化总体的倾向［13］,分析结果一般有增大、减小、不变3种。本文采用线性趋势回归检验法、Mann-Kendall趋势检验法、Spearman秩次相关检验法对花园口水文站径流量变化趋势进行分析。

2.3.1 线性趋势回归检验法

对于检验自变量与因变量之间是否存在线性关系,序列xt（t＝1,2,…,n)的线性趋势成分Yt与时序t的线性回归方程为

其中a和b的估计式为

式中：Yt为因变量；a为常数；b为回归系数；＾a和＾b分别为a和b的估计值；t为时序；ξt为残差项；¯x、¯t分别为xt和t的均值。

构造统计量：

式中：d为服从t分布的函数；为的方差为残差项平方和与自由度的比值。

式（16)服从自由度为（n-2)的t分布［14］。 假设原序列无趋势性,按照式（16)～式（19)计算d,选择显著水平α＝0.05,在t分布表中查出临界值与计算的d值比较,当时,拒绝原假设,序列趋势性显著。按照上述方法对突变点划分的3个阶段进行线性趋势回归检验,结果见表3。

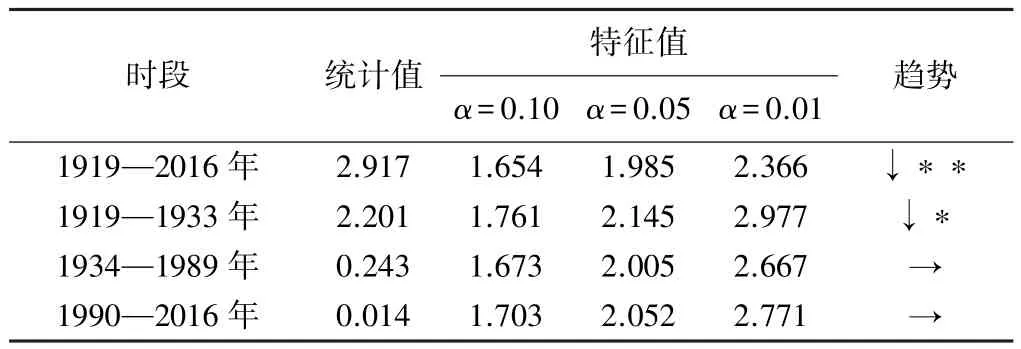
表3 年径流量线性趋势回归检验结果

由表3可知,数据序列总体变化趋势较为显著,通过0.01的显著性检验,其中：1919—1933年变化趋势相对显著,通过0.05的显著性检验；1934—1989年、1990—2016年变化趋势平稳。

2.3.2 Mann-Kendall趋势检验法

运用Mann-Kendall趋势检验法进行趋势分析时,同样不要求被分析样本遵从一定分布,该方法是关于观测值序列的秩次和时序的秩次相关检验,原假设H0为时间序列xt（t＝1,2,…,n)n个独立的随机变量同分布的样本,Mann-Kendall检验法中的统计变量S计算公式为

其中

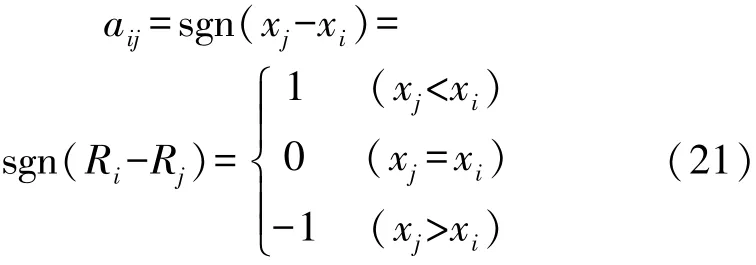
式中：Ri和Rj分别为xj和xi的秩次；n为序列长度。

当n＞8,假设实测数据服从独立且同分布,统计量S服从正态分布,其均值和方差满足：

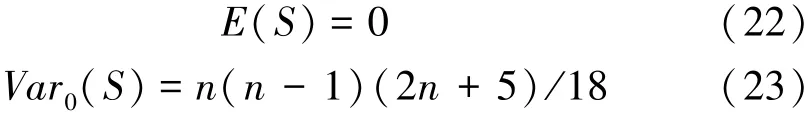
标准正态分布统计量计算式为

在趋势检验中,选择显著性水平α＝0.10,当｜Z｜＜时,接受原假设,即趋势不显著；反之,则趋势显著。统计变量Z＞0时,序列存在上升趋势；Z＜0时,序列存在下降趋势。另选取显著性水平α＝0.05及α＝0.01检验趋势显著程度。根据上述方法分析花园口水文站年径流量变化趋势,结果见表4。

表4 年径流量Mann-Kendall趋势检验结果

从表4可以看出,数据序列总体趋势显著,通过0.05的显著性检验,统计值小于零,总体呈现下降趋势,其中：1919—1933年变化趋势相对显著,通过0.10的显著性检验,表现为下降趋势；1934—1989年、1990—2016年变化趋势平稳。

2.3.3 Spearman秩次相关检验法

Spearman秩次相关检验法是通过分析时间序列xt与其时序t的相关性来检验其趋势性的方法［15］。xt用其秩次Rt（Rt为将xt从大到小排序所对应的序号)代表,秩次相关系数计算式为

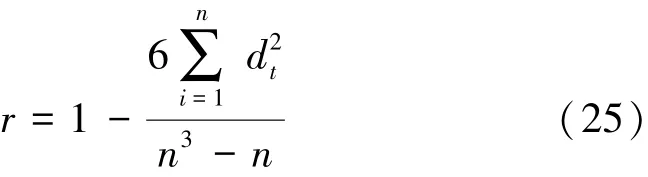
式中：dt为变量从大到小排序的序号与变量对应的时序之间的差值,dt＝Rt-t。

秩次Rt与时序t越接近,则dt的值就越小,秩次相关系数r就越大,趋势性就越显著。相关系数是否异于0,用t检验法,统计量计算式为

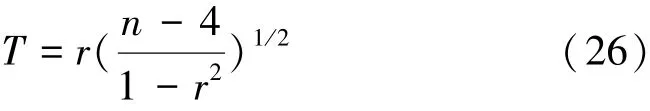
式（26)服从自由度为（n-2)的t分布。假设序列无趋势,将计算出的T与在t分布表中查得的显著性水平α＝0.05对应的临界值则拒绝原假设,序列趋势显著；反之,序列趋势不显著,另选取显著性水平α＝0.01检验趋势显著程度。根据上述方法分析花园口水文站年径流量变化趋势,结果见表5。

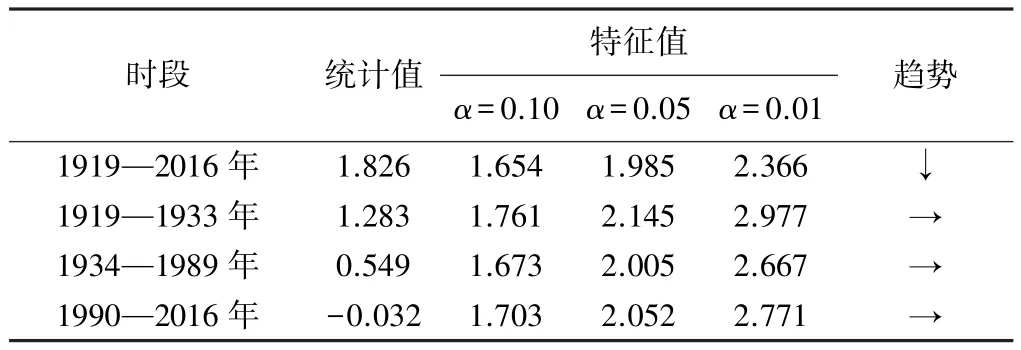
表5 年径流量Spearman秩次检验结果

从表5可以看出,数据序列总体趋势显著,通过0.10的显著性检验。根据对突变点划分的3个阶段分析,趋势表现平稳,均未通过0.10的显著性检验。

2.3.4 趋势综合分析

对以上趋势检验分析方法得到的结果进行综合,假如某种方法检验趋势显著,则记为“1”,否则记为“-1”,将各种检验方法的加和作为径流时间序列的综合趋势（见表6)。

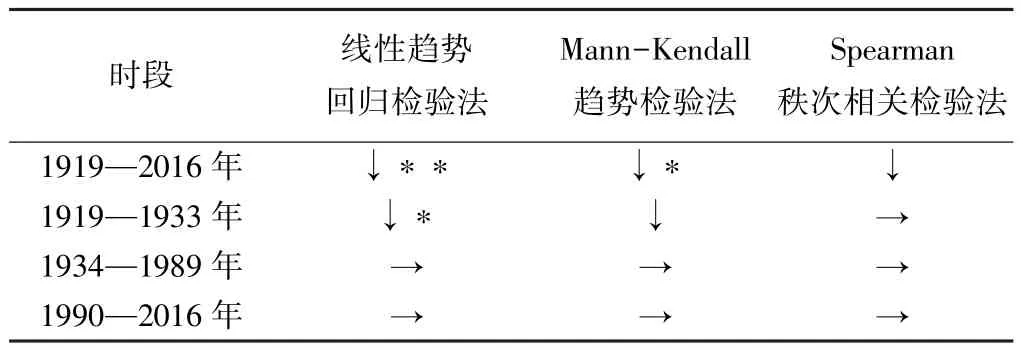
表6 年径流量各方法检验结果

从表6可以看出：总体趋势较为显著；1919—1933年减小趋势显著,两种方法的结果均通过0.10的显著性检验；1934—1989年、1990—2016年的趋势较为平稳。综合以上分析,花园口年径流量的突变形式为跳跃突变,1934—1989年的平均年径流量比1919—1933年增长122亿m3,而1990—2016年的平均年径流量显著下降,比1934—1989年约减小163亿m3（见图5)。

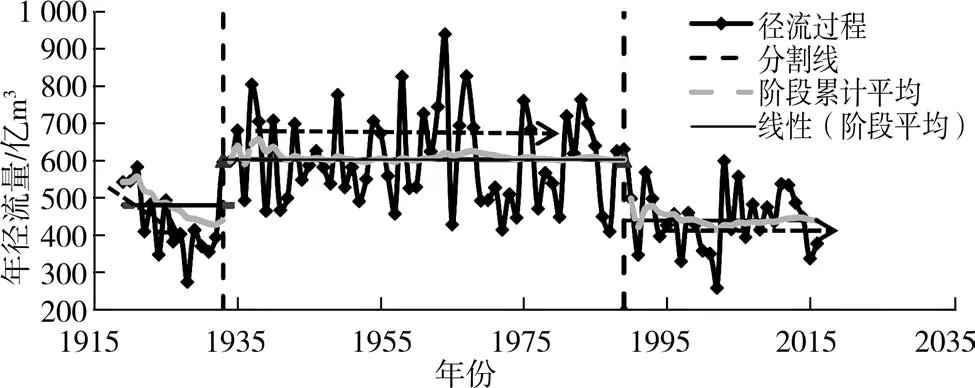
图5 花园口水文站年径流量变异前后综合趋势检验

3 结 论

（1)综合有序聚类分析法、Mann-Kendall突变检验法、滑动t检验法分析结果,花园口径流时间序列在1933—1934年、1989—1990年发生了突变,突变原因前者主要为自然因素（气温、降水)大尺度的变化,后者主要为人为因素（用水增加、下垫面改变)流域尺度的变化。

（2)综合线性趋势回归检验法、Mann-Kendall趋势检验法、Spearman秩次相关检验法分析结果,花园口径流时间序列在1919—1933年下降趋势显著（通过了0.10的显著性检验)；1934—1989年、1990—2016年径流量变化相对稳定。径流时间序列的突变类型为跳跃突变,按突变点划分的3个阶段年径流量平均值相差较大。

黄河流域面积较大,河川径流的演变比较复杂,在以后的研究中,应结合上中游其他重要水文站,分析黄河不同河段的径流演变特性。