起拱对钢筋混凝土空腹夹层板内力影响的参数化分析
(贵州大学空间结构研究中心, 贵州贵阳550003)
0 引言
钢筋混凝土空腹夹层板是由表层薄板、上下肋及剪力键构成,其构造如图1所示,空腹夹层板结构主要适用于大跨度多层建筑的楼盖及屋盖[1-2]。目前,贵州省和黑龙江省[3-4]已出台相应技术规程以指导空腹夹层板在工程中的应用,已建成工程有安徽合肥市合肥工业大学食堂、广东清远市开发区剧场屋盖、贵州兴仁县三鑫酒店会议厅等。空腹夹层板从研发至今,学者们已做了大量研究:文献[5-6]讨论了空腹夹层板的承载力设计问题,并将其与有限元结果做了详细比较;文献[7-8]表明表层薄板可显著提高楼盖结构竖向刚度;文献[9-10]分析了楼盖结构的振动加速度响应和加速度自功率谱,表明结构舒适度满足规范要求。由上述可知,学者们主要集中于对其设计计算方法、静力受力性能和舒适度的研究。

(a) 空腹夹层板轴测图

(b) 空腹夹层板剖面示意图
图1 钢筋混凝土空腹夹层板示意图
Fig.1 Schematic diagram of reinforced concrete open-web sandwich plate
混凝土结构在施工时一般需要按照相关规范进行预起拱[11]。文献[12]主要从设计和施工技术两方面研究了混凝土结构的起拱问题,以求达到合理的起拱效应和经济效益;文献[13]通过对实际工程分析,确定了合理的预起拱值;文献[14]提出了钢筋混凝土梁和单向板拱形作用行为的模型,并研究了影响起拱效应的因素。综上所知,混凝土结构的起拱研究具有一定价值和意义。钢筋混凝土空腹夹层板的使用跨度为18~30 m,其跨度大,起拱后结构中存在附加内力,该内力会使结构实际内力与设计内力产生一定偏差,因此分析起拱对结构受力和安全性的影响显得尤为重要。
为分析起拱对钢筋混凝土空腹夹层板内力的影响,本文采用参数化分析方法,利用有限元软件建立7个未起拱模型和与其对比的21个起拱模型,对影响结构起拱内力的参数:起拱坡度、内力所在层、跨度、活载取值、地震烈度逐一分析。结果表明:结构起拱内力与设计内力存在差异。上肋和剪力键起拱轴压力增大,需对其设计轴压力进行调整、放大,以满足结构的安全性要求;薄板起拱拉应力大幅度减少,从经济性角度考虑,建议对板顶、板底设计拉应力进行折减;边梁起拱水平剪力、水平面内弯矩和上下肋起拱轴拉力减少,从安全储备角度考虑,可以采用设计内力进行设计。
1 参数定义及模型建立
1.1 参数介绍及定义
钢筋混凝土空腹夹层板常用跨度[3-4]为18~30 m,SAP2000建立的28个4层结构模型分别为:7个未起拱模型,以及7×3个上述跨度、三种起拱坡度组成的起拱模型。由于模型的长宽比皆为1,起拱时按照文献[3-4],从四周向中间起拱,越到跨中位置起拱值越大。图2给出了起拱示意图:图2(a)、(b)中各点划线组成的方框,代表起拱数值在此处相同;图2(c)为起拱时的展开立面图。根据文献[3-4],本文考虑的起拱坡度分别为:0.1 %、0.2 %、0.3 %,以下分别简称为:Ⅰ型起拱、Ⅱ型起拱、Ⅲ型起拱。
本文对分析的28个模型,恒载均采用4 kN/m2,记为D;活载包含2 kN/m2、3 kN/m2、4 kN/m2三种取值,分别记为L1、L2、L3。荷载取值参考文献[15]给出,分别涵盖了会议厅、剧场、舞台等常用建筑的荷载取值。空腹夹层板的混凝土均采用C45,配筋采用HRB400钢筋。不失一般性,结构抗震设防烈度包含6度、7度、8度,设计基本地震加速度值分别为0.05 g、0.10 g、0.20 g,设计地震分组为第三组,建筑场地为Ⅱ类;采用振型分解反应谱法进行多遇地震分析,三向地震影响系数最大值按1∶0.85∶0.65调整[16]。
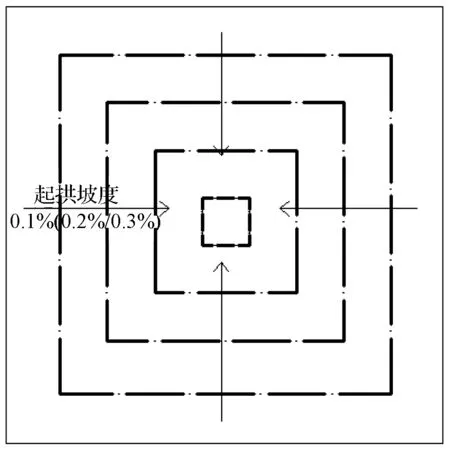
(a) 起拱模型示意图
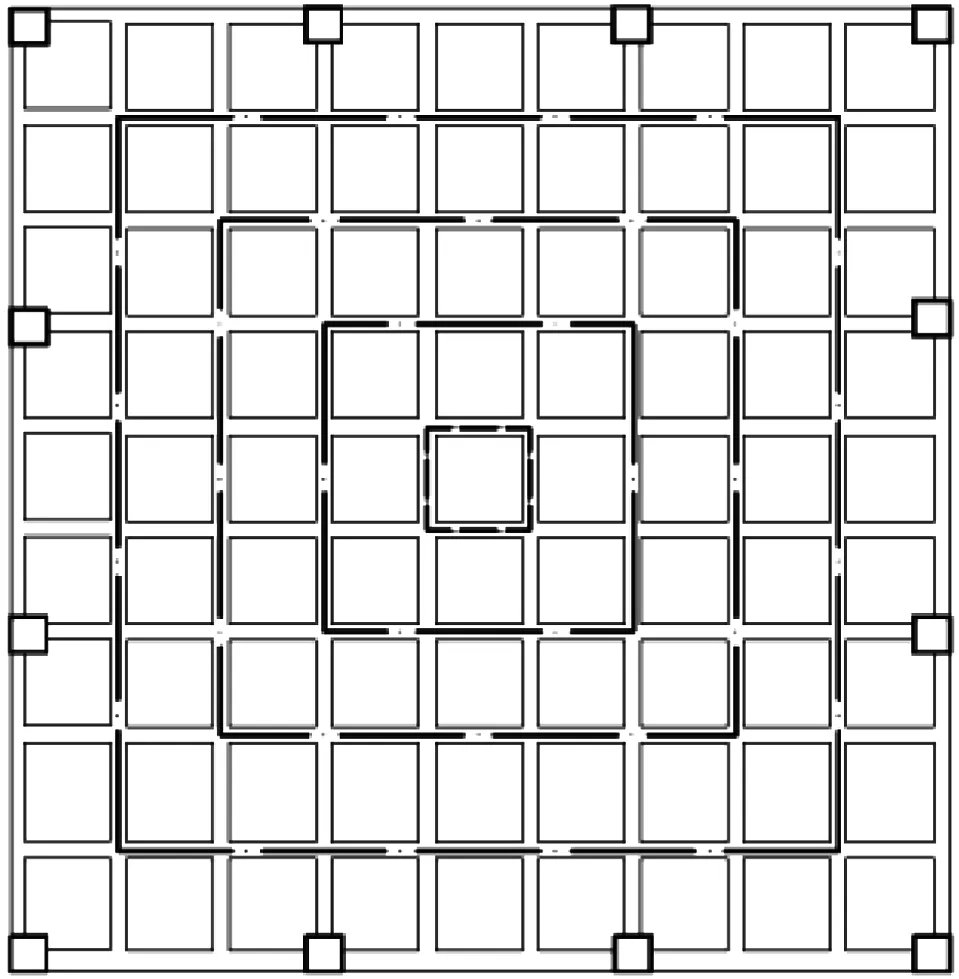
(b) 起拱平面示意图

(c) 起拱展开立面图
1.2 有限元模型建立
建模时,在18~30 m跨范围内,取用18 m、20 m、22 m、24 m、26 m、28 m、30 m这7种跨度值,表1给出了7个未起拱模型的轴测图及其自振周期。模型各层表层薄板厚度统一采用100 mm,空腹夹层板网格尺寸均为2 m,柱子间距均不超过8 m。经模型试算和数据整理分析,提取具代表性的工况组合见表2;结构各构件截面尺寸见表3,各跨度起拱模型与相应未起拱模型采用相同的构件截面尺寸。由于在边梁处没有剪力键,上、下肋与边梁的两个交接处设置耦合,采用BODY束缚,以模拟边梁对上、下肋的约束作用。


表1 18~30 m跨空腹夹层板未起拱模型及其自振周期Tab.1 Un-arched modelsand self-vibration period of 18~30m spanned open-web sandwich plate
注:由于三种起拱坡度的起拱模型与其相应未起拱模型的自振周期相差很小,故而本表只给出了未起拱模型的自振周期。

表2 工况组合表Tab.2 Working condition combination
注:Qx1的第一个下标x表示地震力方向为x向,第二个下标1表示地震烈度为6度,其他表示与此类似;当其第二个下标为2、3时分别表示地震烈度为7、8度。
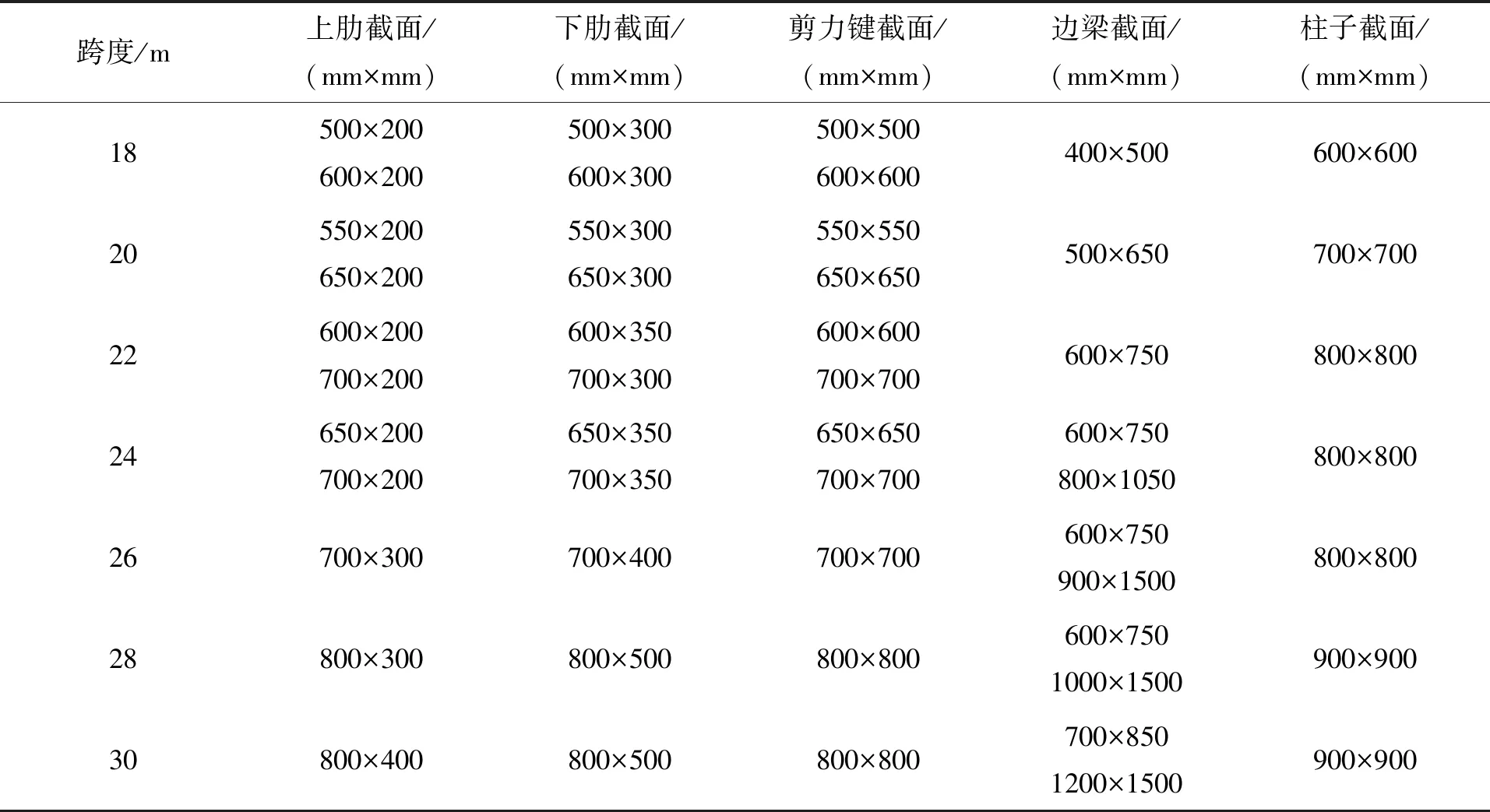
表3 结构构件截面尺寸Tab.3 Structural member sectional size
注:表中同一跨度,若有两个截面取值,其中较大截面用于模型底层。
2 起拱对边梁内力影响
边梁竖向剪力、竖向平面内弯矩和轴力受起拱影响较小,本节主要针对边梁水平剪力和水平面内弯矩在Ⅰ、Ⅱ型和Ⅲ型起拱时的变化情况进行分析。在分析三种起拱坡度时,主要讨论内力所在层、活载、地震烈度和跨度这四种参数变化对其内力差值比的影响。
2.1 Ⅰ、Ⅱ型起拱对边梁内力影响
2.1.1 内力所在层影响
分析内力所在层对边梁起拱内力影响时,取用C1工况组合作为代表。图3给出了边梁水平剪力、水平面内弯矩的差值比图。由图3可知:Ⅰ、Ⅱ型起拱时,不同层的水平剪力差值比最大相差分别为5 %、9 %左右;不同层的水平面内弯矩差值比最大相差13 %左右;说明内力所在层对边梁水平剪力、水平面内弯矩差值比有影响。总体来看,边梁的水平剪力、水平面内弯矩差值比均为负数,表明设计内力大于起拱内力,采用设计内力是偏于安全的。为方便对比,本文后续以差值比绝对值较大的一层数据为代表分析其他参数对内力差值比的影响。
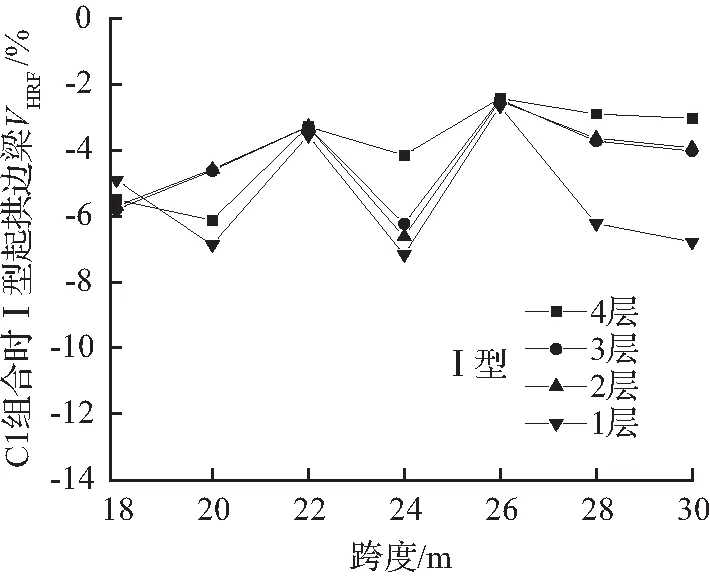
(a) C1组合时Ⅰ型起拱边梁VHRF图
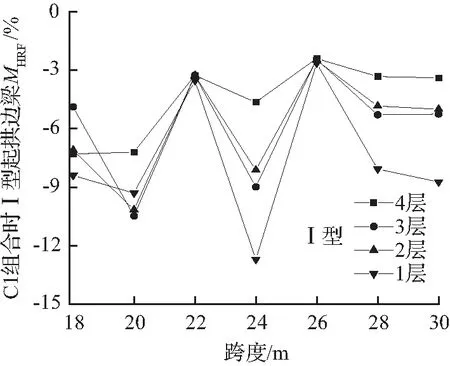
(b) C1组合时Ⅰ型起拱边梁MHRF图
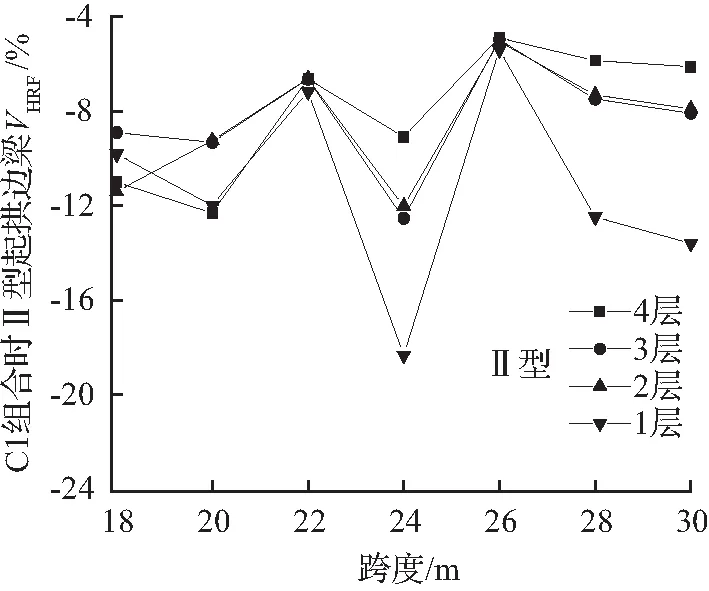
(c) C1组合时Ⅱ型起拱边梁VHRF图
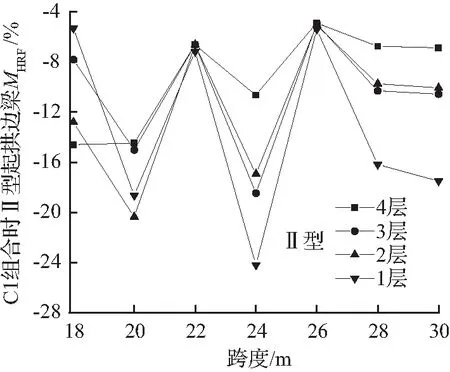
(d) C1组合时Ⅱ型起拱边梁MHRF图
图3 C1组合时Ⅰ、Ⅱ型起拱边梁VHRF、MHRF图
Fig.3VHRFandMHRFdiagrams of side beam for type I and II arching with C1 combination
2.1.2 活载影响
分析活载对边梁起拱内力影响时,取用C1、C3、C5三种工况组合。由图4可知,Ⅰ、Ⅱ型起拱时,边梁水平剪力和水平面内弯矩的差值比几乎不受活载改变的影响。

(a) C1、C3、C5组合时边梁VHRF图

(b) C1、C3、C5组合时边梁MHRF图
图4 C1、C3、C5组合时Ⅰ、Ⅱ型起拱边梁VHRF、MHRF图
Fig.4VHRFandMHRFdiagrams of side beam for type I and II arching with C1, C3, C5 combination
2.1.3 地震烈度影响
分析地震烈度对边梁起拱内力影响时,取用C2、C4、C6三种工况组合为代表。由图5可知,Ⅰ、Ⅱ型起拱时,边梁水平剪力和水平面内弯矩的差值比几乎不受地震烈度改变的影响。
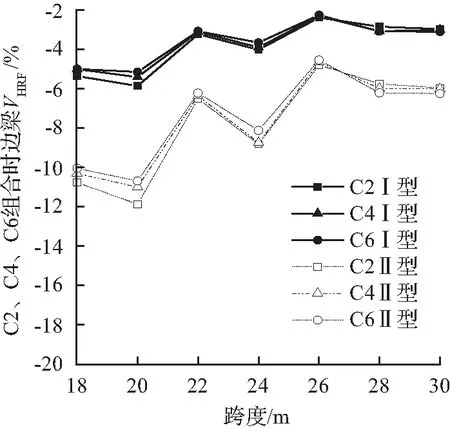
(a) C2、C4、C6组合时边梁VHRF图

(b) C2、C4、C6组合时边梁MHRF图
图5 C2、C4、C6组合时Ⅰ、Ⅱ型起拱边梁VHRF、MHRF图
Fig.5VHRFandMHRFdiagrams of side beam for type I and II arching with C2, C4, C6 combination
2.1.4 跨度影响
由图4、5可知:Ⅰ、Ⅱ型起拱时,相邻跨度的内力差值比最大相差分别为4 %、8 %左右;由此说明跨度会对边梁起拱内力产生影响,且此影响随起拱坡度增大而增强。
2.2 Ⅲ型起拱对边梁内力影响
2.2.1 内力所在层影响
图6给出了边梁Ⅲ型起拱时的水平剪力、水平面内弯矩的差值比图。由图6(a)、(b)可知:Ⅲ型起拱时,不同层的水平剪力差值比最大相差约为13 %;不同层的水平面内弯矩差值比最大相差约为16 %。由此可知:Ⅲ型起拱时,内力所在层对边梁水平剪力、水平面内弯矩差值比有较大影响。由于边梁上述内力差值比均为负值,说明设计内力较起拱内力偏大,采用设计内力分析足够安全。
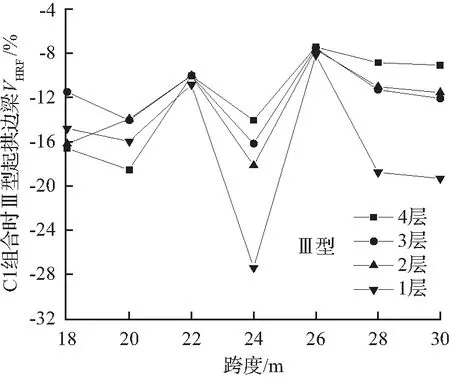
(a) C1组合时边梁VHRF图
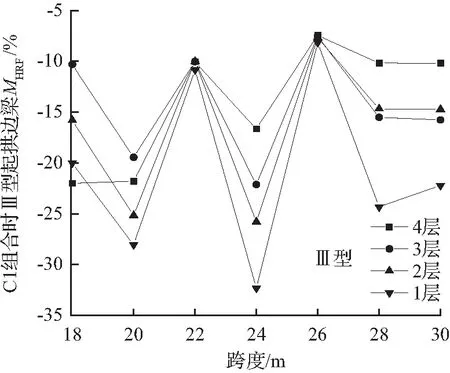
(b) C1组合时边梁MHRF图
图6 C1组合时Ⅲ型起拱边梁VHRF、MHRF图
Fig.6VHRFandMHRFdiagrams of four-layer model for type Ⅲ arching with C1 combination
2.2.2 活载、地震烈度影响
Ⅲ型起拱时,分析活载对边梁起拱内力的影响,采用C1、C3、C5工况组合。由图7(a)、(b)可知:活载改变对边梁水平剪力和水平面内弯矩差值比几乎无影响。另外,地震烈度也几乎不会影响边梁水平剪力和水平面内弯矩差值比,这部分就不再赘述。

(a) C1、C3、C5组合时边梁VHRF图

(b) C1、C3、C5组合时边梁MHRF图
图7 C1、C3、C5组合时Ⅲ型起拱边梁VHRF、MHRF图
Fig.7VHRFandMHRFdiagrams of side beam for type Ⅲ arching with C1,C3,C5 combination
2.2.3 跨度影响
由图7可知,相邻跨度的边梁内力差值比最大相差约为12 %,说明Ⅲ型起拱时,跨度对边梁水平剪力和水平面内弯矩的差值比有一定影响。
2.3 小结
综合2.1和2.2节分析结果可知:①起拱坡度越大,边梁起拱内力越小,内力所在层、跨度会对边梁起拱内力产生一定影响;活载和地震烈度对起拱内力影响极小。②边梁的起拱内力小于其设计内力,从安全储备角度考虑,可以采用设计内力进行设计。
3 起拱对空腹夹层板内力影响
上、下肋和剪力键的剪力、弯矩受起拱影响较小,本节主要针对上述构件的轴力在Ⅰ、Ⅱ型和Ⅲ型起拱时的变化情况进行分析。
3.1 Ⅰ、Ⅱ型起拱对上下肋、剪力键内力影响
由于Ⅰ、Ⅱ型起拱时,下肋轴力差值比较小,本节仅针对绝对值数值较大的上肋轴力差值比和剪力键轴压力差值比进行讨论。
3.1.1 内力所在层影响
分析内力所在层对上肋和剪力键轴力差值比影响时,取用C1工况组合。图8给出了上肋轴力差值比、剪力键轴压力差值比图。由图8(a)、(b)可知:Ⅰ、Ⅱ型起拱时,上肋不同层轴力差值比最大相差约2 %,由此说明内力所在层对上肋轴力差值比影响很小。由图8(c)可知:在18~26 m跨,剪力键不同层轴压力差值比最大相差约为2 %,表明内力所在层对18~26 m跨的剪力键轴压力差值比影响很小。由于上肋轴拉力差值比为负值,说明上肋起拱轴拉力小于其设计轴拉力;上肋轴压力和剪力键轴压力差值比均为正值,说明上述起拱轴压力大于其设计轴压力。
图8 C1组合时Ⅰ、Ⅱ型起拱上肋、剪力键NRF图
Fig.8NRFdiagrams of top rib and shear key for type I and II arching with C1 combination
3.1.2 活载、地震烈度影响
分析活载对上肋起拱轴力、剪力键起拱轴压力影响时,取用C1、C3、C5三种工况组合为代表。分析地震烈度对其影响时,取用C2、C4、C6三种工况组合。由图9可知,Ⅰ、Ⅱ型起拱时,上肋轴力差值比和剪力键轴压力差值比几乎不受活载改变的影响。另外,由图10可知:Ⅰ、Ⅱ型起拱时,地震烈度几乎不影响上肋轴力差值比和剪力键轴压力差值比。
图9 C1、C3、C5组合时Ⅰ、Ⅱ型起拱上肋、剪力键NRF图
Fig.9NRFdiagrams of top rib and shear key for type Ⅰ and Ⅱ arching with C1, C3, C5 combination
图10 C2、C4、C6组合时Ⅰ、Ⅱ型起拱上肋、剪力键NRF图
Fig.10NRFdiagrams of top rib and shear key of type Ⅰ and Ⅱ with C2, C4, C6 combination
3.1.3 跨度影响
由图9、10可知:Ⅰ、Ⅱ型起拱时,相邻跨度轴力差值比的最大差值分别约为2 %、4 %。由此说明:Ⅰ、Ⅱ型起拱时,跨度对上肋轴力和剪力键轴压力差值比影响很小。
3.2 Ⅲ型起拱对上下肋、剪力键内力影响
由于Ⅲ型起拱时,下肋轴压力差值比相对比较小,本节只针对绝对值数值相对较大的上肋轴力差值比、下肋轴拉力差值比和剪力键轴压力差值比进行分析。
3.2.1 内力所在层影响
分析内力所在层对上下肋和剪力键轴力差值比影响时,取用C1工况组合。图11给出了上肋轴力、下肋轴拉力差值比和剪力键轴压力差值比图。由图11(a)、(b)、(c)可知:Ⅲ型起拱时,不同层上肋轴力、下肋轴拉力差值比的最大差值均未超过3 %,说明内力所在层对其影响均很小;由图11(d)可知:Ⅲ型起拱时,18~26 m跨范围内,不同层剪力键轴压力差值比的最大差值约为2 %,说明内力所在层对18~26 m跨的剪力键轴压力差值比影响也很小。另外,由图11可知,上下肋轴拉力差值比皆为负数,上肋、剪力键轴压力差值比皆为正数,由此说明:上下肋起拱轴拉力小于其设计轴拉力,上肋、剪力键起拱轴压力大于其设计轴压力。
图11 C1组合时Ⅲ型起拱上下肋和剪力键NRF图
Fig.11NRFdiagrams of top and bottom rib as well as shear key for type III with C1 combination
3.2.2 活载、地震烈度影响
分析活载影响时,取用C1、C3、C5三种工况组合;分析地震烈度影响时,取用C2、C4、C6三种工况组合。由图12可知,Ⅲ型起拱时,上肋轴力差值比、下肋轴拉力差值比和剪力键轴压力差值比几乎不受活载改变的影响。另外,Ⅲ型起拱时,地震烈度几乎不影响上述内力差值比,此部分不再赘述。
3.2.3 跨度影响
由图12可知:Ⅲ型起拱时,相邻跨度轴力差值比的差值最大约为4 %,由此说明跨度对上下肋轴拉力、上肋轴压力以及剪力键轴压力差值比影响较小。
3.3 小结
综合3.1和3.2节分析结果可知:①18~26 m跨范围内,上下肋起拱轴力和剪力键起拱轴压力几乎不受内力所在层影响;活载和地震烈度改变对起拱轴力影响极小;跨度对起拱轴力有一定影响。②上肋和剪力键起拱轴压力均大于其设计轴压力,为保证结构安全,需对设计轴压力乘以调整系数,以便进行结构设计;调整系数由表4给出,该调整系数考虑了内力所在层、活载、地震烈度的影响。③上下肋起拱轴拉力均小于设计轴拉力,从安全储备角度考虑,采用设计轴拉力分析是可行的。

图12 C1、C3、C5组合时Ⅲ型起拱上下肋及剪力键NRF图Fig.12 NRF diagrams of top and bottom rib as well as shear key for type III arching with C1, C3, C5 combination

4 起拱对空腹夹层板表层薄板应力影响
本节只针对变化幅度较大的板顶和板底起拱拉应力进行分析。不同的起拱坡度、活载和地震烈度对薄板起拱应力影响比较接近,故而只对C1工况组合时Ⅰ型起拱薄板的拉应力进行讨论。由于模型长宽比均为1,薄板两方向应力变化一致,只取薄板水平向应力分析。
活载、地震烈度改变对薄板拉应力差值比影响很小,可忽略不计。由图13(a)可知,不同层薄板顶面拉应力差值比的最大差值可达30 %,薄板顶面拉应力差值比受内力所在层影响较大;对同一层相邻跨度的顶面拉应力差值比比较可知,其最大差值可达14 %,说明跨度对薄板顶面拉应力差值比有一定影响。与此相对应,由图13(b)可知,薄板底面拉应力差值比受内力所在层、跨度影响相对较小。
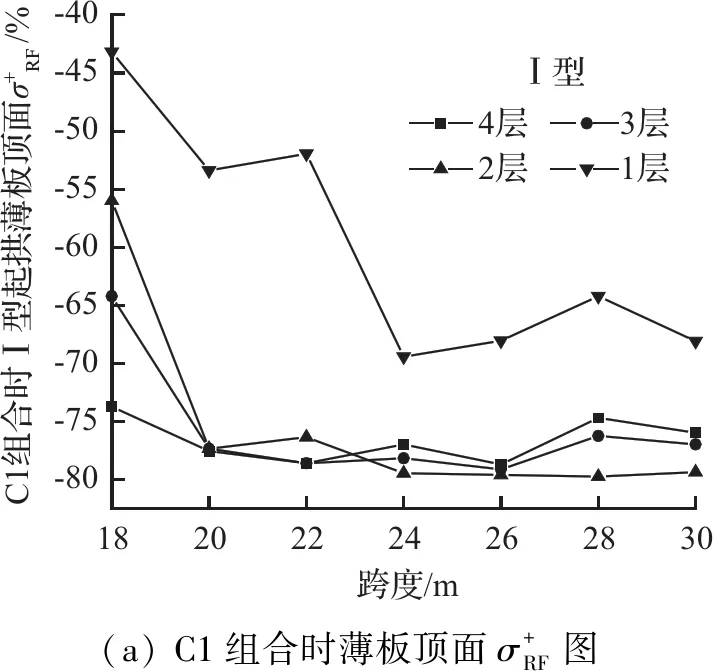
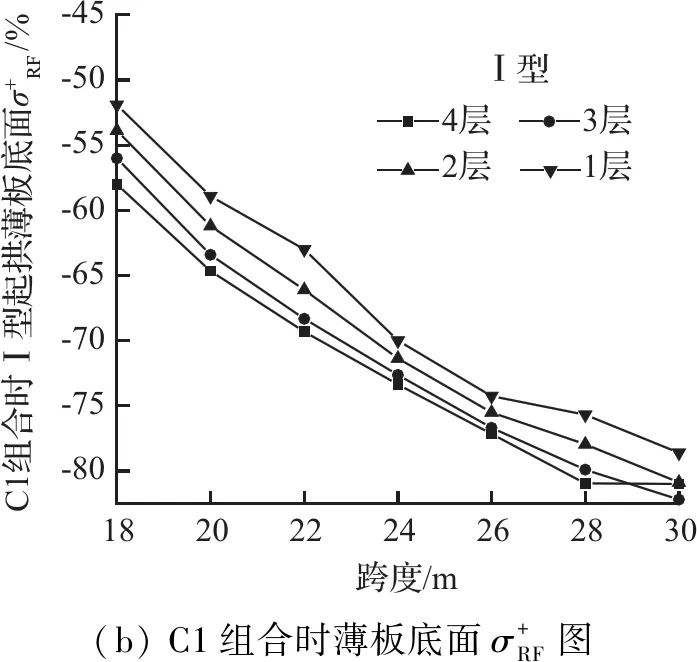
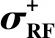

由于薄板拉应力差值比均为负数且绝对值多大于40 %,说明薄板设计应力远大于起拱应力。从经济性角度出发,可将薄板设计应力乘以折减系数,以考虑实际施工起拱的影响。应力折减系数如表5所示,该值均采用4层中的最大数值,以确保有足够安全度和冗余量。

表5 18~30 m跨薄板设计拉应力折减系数Tab.5 Design tensile stress reduction factor of thin plate for 18~30 m span
5 算例验证
为验证表4和表5中数值的准确性,需取其他跨度模型进行验证。利用SAP2000建立21 m×21 m的4层空腹夹层板模型,包括未起拱模型和Ⅰ、Ⅱ、Ⅲ型起拱模型,如表7所示。模型边界条件设置与前述跨模型一致,荷载工况同表2;模型各构件截面尺寸同22 m跨,如表3所示;模型网格尺寸为2.1 m,柱子间距不超过8 m,薄板厚度采用100 mm。

表7 21 m跨空腹夹层板模型Tab.7 Open-web sandwich plate model for 21 m span
由Ⅱ、Ⅲ型起拱模型的起拱轴压力和未起拱模型的设计轴压力之比,得到设计轴压力调整系数,表8给出了C1工况组合时的相关调整系数。由模型的薄板起拱应力和设计应力之比,得到薄板应力折减系数,表9给出了C1工况组合时Ⅰ型起拱的折减系数。由表8、9可知,由模型得到的调整系数、折减系数与预测值非常相近,误差很小,表明表4、表5具有一定可靠性,可以运用于工程实践。

表8 21 m跨模型所得设计轴压力调整系数与其预测调整系数对比Tab.8 Comparison of design axis pressure adjustment coefficients between obtaining from 21 m span model and prediction
注:21 m跨预测的设计轴压力调整系数是由表4线性插值所得。

表9 21 m跨模型所得薄板设计拉应力折减系数与其预测折减系数对比Tab.9 Comparison of design tensile stress reduction factors of thin plate between obtaining from 21 m span model and prediction
注:21 m跨设计拉应力折减系数的预测值是由表5线性插值所得。
6 结论
①起拱坡度越大,起拱内力较设计内力差别越大;活载、地震烈度改变对空腹夹层板各组成构件和边梁的起拱内力几乎无影响;跨度对上下肋和剪力键以及边梁起拱内力有一定影响。
②边梁起拱内力小于其设计内力,上下肋和剪力键起拱轴拉力小于其设计轴拉力,从安全储备角度考虑,可以采用其设计内力进行设计。
③上肋和剪力键的起拱轴压力大于其设计轴压力,为保证结构的安全性,需对其设计轴压力进行调整、放大,调整系数如表4所示。
④表层薄板板顶、板底起拱拉应力远小于其设计拉应力,从经济性角度考虑,建议对板顶、板底设计拉应力进行折减,折减系数如表5所示。

