(2+1)维广义浅水波方程的非局部对称及精确解

张琳琳,吕海玲

(1.聊城大学 数学科学学院，山东 聊城 252059;2.枣庄学院，山东 枣庄 277160 )

0 引言

非线性微分方程在很多领域有着重要的应用，如量子理论[1～2]、有限元[3～4]等，求解非线性微分方程一直是数学家研究的重要方向之一.19世纪，挪威数学家Sophus Lie从求解微分方程入手，依靠微分几何方法和射影几何方法建立起一种变换[5]，这种变换将空间直线簇和球面一一对应.不久又引入了一般的连续变换群的概念，此变换群可将微分方程的解表示出来并加以分类，这就是我们现在研究的Lie变换群[6～7].经过多年的研究，Lie群的概念得到了飞速的发展，产生了很多推广方法，如经典、非经典Lie群方法，广义条件对称方法，特别是近些年由Vinogradov和Krasil’shchik提出的非局部对称，不管是从理论还是应用方面都得到了很大的飞跃，拓展了Lie群方法的应用范围，得到了以往方法难以构造的新结果.1988年Bluman提出了势对称的概念，利用方程的势系统构造非局部对称，此方法非常有效，并且可以应用计算机求解，不仅提高了运算的准确性，而且扩展了非局部对称的范围.2012年楼森岳等[8]，利用Darboux变换、 Bäcklund 变换构造非局域对称，并成功地把非局域对称局域化，给出了KdV方程一些新的精确解，如椭圆周期波和孤立子的相互作用解，这些新的结果为研究这些方程的物理机制指明了方向.

在研究非局域对称的过程中发现[9～11]，非局部对称都是与一些辅助系统有关系，如势系统、Bäcklund变换等，通过引入不同的辅助系统，可以构造方程不同类型的非局域对称，这些对称可以用来构造系统的新的精确解、守恒律等工作.

本文将利用广义浅水波方程的Lax对作为辅助系统，构造方程的非局部对称及精确解，(2+1)维广义浅水波方程有下面的形式，

uxt+auxuxy+buyuxx+cuxy+duxxxy=0

(1)

其中a,b,c,d为任意常数.

当a=b=d=1,c=0时,方程转化为一般的浅水波方程.当a+b=-6,c=0,d=1，则方程转化为著名的KdV方程uxt-6uxuxx+uxxxx=0.据我们查询所知，此方程的非局部对称还没有人研究，因此研究此方程的非局部对称及精确的相互作用解是非常有意义的工作.在研究方程的非局部对称之前，我们先利用截断Painlevé分析研究此方程的Schwartzian形式，为后面非局部方程的应用打好基础.

1 (2+1)维广义浅水波方程的截断Painlevé分析

(2)

首先我们对方程(2)做Painlevé截断分析，通过领头项分析可知，可以假设方程(2)具有下面形式的解，

(3)

其中u0,u1是(x,y,t)的函数，φ=φ(x,y,t)是一个任意的奇异流形.通过计算可知，

(4)

因此得到(3)的具体形式为，

而且，方程(2)满足下面Schwartzian形式，

(5)

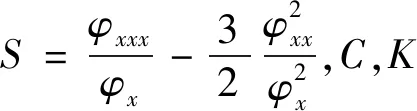
我们知道，方程的Schwartzian形式(5)在Möbius变换下是不变的，

(6)

因此，可以通过(5)的解，以及变换(6)构造新的精确解.

2 (2+1)维广义浅水波方程的的非局部对称

为了构造方程(2)的非局部对称，首先给出方程的Lax对[12]，

ψxx=-uxψ,

(7)

通过相容性条件ψxxt=ψtxx即可得到方程(2).

通过计算可知，方程(2)的对称满足下面线性方程，

(8)

对称σ1具有下面的形式，

(9)

(10)

σ1=ψ2.

(11)

由于非局部对称不可以直接用来构造群不变解，因此我们需要构造一个扩大系统，使之Lie对称等价于方程(2)的非局部对称，由Lax对(7)可得，

(12)

其中变换u→u+εσ1,ψ→ψ+εσ2.

为了求得σ2，根据方程组(12)可以令

σ2=ψφ，

(13)

把(11)(13)带入(12)可得下面相容方程组，

(14)

而且可以验证，变量φ满足方程(2)的Schwartzian形式(5)，这为我们后面计算带来的方便，而且φ满足的对称为σ3=φ2.因此方程组(2)，(7)，(14)称为封闭系统，利用得到的对称，可以构造系统的群不变解，求解下面初值问题，

(15)

求解(15)得到，

(16)

例如，我们给出方程(2)的一个简单的解u=2tanh(x)，可以计算ψ,φ满足

把上述解 带入到(16)式即可已得到方程(2)新的精确解，由于式子比较繁琐，这里就不再给出了.

3 (2+1)维广义浅水波方程新的精确解

为了利用非局部对称得到更多的精确解，我们可以利用封闭系统的Lie对称来研究，为此，先研究封闭系统的Lie对称.

因为封闭系统的对称满足方程(8)(12)以及

(17)

假设σ1,σ2,σ3具有下面的格式，

σ1=Xux+Yuy+Tut-U,
σ2=Xψx+Yψy+Tψt-P1,
σ3=Xφx+Yφy+Tφt-P2,

(18)

其中X,Y,T,U,P1,P2均为(x,y,t,u,b,c,ψ,φ)的函数，把(18)式以及封闭系统代入到(8)(12)及(17)式中，利用决定方程组得到下面结果，

X=c3x+F1(t),Y=c3(2ct-2y)+c1y+c4,T=c1t+c2,

(19)

其中，ci,i=1...3为任意常数，Fj,j=1...5为相应变量的任意函数.从(19)可以看出，封闭系统的Lie对称包含了方程(2)的非局部对称，因此把非局部对称等价的转化为了Lie对称，下面利用Lie对称构造方程的精确解.

(20)

得

(21)

我们把(21)式代入到封闭系统(2)(7)(14)里得到Ψ,U满足下面形式，

(22)

因此只要求出Φ，系统的解即可得到，又知道φ满足Schwartzian形式(5)，故把(21)带入(5)得，

(23)

为了求解方程(23)，先做行波变换，令Φ(ξ,η)=Φ(ξ+μη)=Φ(Δ)，得，

再令ΦΔ=G,则上式变为，

(24)

验证可知，方程(24)等价于下面椭圆方程，

(25)

其中C1,C2为任意常数.

由于，方程(25)为椭圆方程，因此具有椭圆函数解，假设方程具有下面形式解，

G=a0+a1sn(Δ,l)

(26)

其中sn(Δ,l)为Jaccobi正弦函数，a0,a1为待定系数，将(26)代入到(25)中，得到下面四组解，

(27)

a1,α,l为任意常数.

把(27)式带入(26)可得到方程(25)的解，进而由ΦΔ=G可以得到Φ的表达式，最后通过(21)式可以得到原方程的精确解，由于表达式比较庞大，这里就不再给出.而且通过(21)式可以看出，得到的解为扭结孤立子与椭圆函数相互作用解，这种形式的解可以用来解释浅水波中的复杂波的由来.

4 总结

本文主要是利用非局部对称方法研究了(2+1)维广义浅水波方程，由于非局部对称与方程的的Schwartzian形式有着密切的联系，因此文中通过截断Painlevé分析方法构造了方程的Schwartzian形式.又由于方程的非局部对称不能直接用来构造方程的群不变解，因此通过引入新的变量，将非局部对称延拓成封闭的局域系统，而且封闭系统的Lie对称包含原系统的非局部对称，文中利用得到封闭系统的的Lie对称构造了群不变解，并利用非局部对称约化求解原方程，得到了方程的精确解，而且这种形式的解即孤立子解与椭圆周期波解的相互作用解，用一般的Lie对称方法是求不出来的，而且这种相互作用解为解释浅水波中的复杂波提供了科学依据.