最优化原理在动态规划中的应用

日毛吉,张爱萍

(1.西北民族大学 数学与计算机科学学院,甘肃 兰州 730030；2.城关区教师进修学校附设小学，甘肃 兰州 730030)

1 引言

动态规划主要是按照系统状态而进行时间与空间上的阶段性控制，并运用数学方法对各个阶段的状态进行推算，并做出最终最具实效性、最佳经济效益的决策[2].在经济发展的不断推动下，各行各业的生产经营活动的扩张，增加了资金管理、资源管理、能源管理、人力资源管理、公共事业管理等的复杂程度，给管理科学提出了许多新的要求与问题，数学作为管理科学中数量分析方法的基础，解决这些问题具有独特的思路和方法，其中动态规划的思想方法显著的效果得到了广泛的应用[8,10].因为动态规划的方法在处理某些比较复杂的问题进行优化时，比整数规划、目标规划，线性规划和非线性规划等用动态规划比其他方法更方便求解.但实施动态规划需要充足的资金支持和对管理系统进行维护，不仅对系统维护人员和维护费用都需要资金的支持，还要有充足的人力、资金和物质来保障的条件下才能有效进行.动态规划管理在企业发展和市场竞争力的提高中起着重要的作用，它可以优化企业的管理过程，为企业的发展带来重要的保障[1].

动态规划最初是由理查德·贝尔曼(Richard Bellman)在20世纪40年代提出的，是为了叙述并处理某一些比较特殊问题的过程，所以在该过程中不时地寻找最优的决策方案.到1953年，Bellman继续对动态规划问题进行了推理分析，着重提出动态规划的作用是在较大的决策中代入较小的决策问题.1957年Bellman发表了很多学术论文，并出版了他的第一部著作《动态规划》，这本书成为当时应用和研究动态规划理论的唯一书籍.在Bellman与协助他的工作人员正在完善和推广此方法的同时，在时刻关注动态规划发展的其他的一些学者也对此做出了很大的功绩，其中贡献最大的是Aris和Mitten.Aris在三年期间共出版了两部涉及动态规划的著作，并在1964年与Wild.

Nemhauser联手创立了解决分枝、循环性多阶段决策系统的一套理论.

自从动态规划在我国应用开始，很多学者对动态规划进行了详细的研究，2014年赵娟、樊超[3]对动态规划的使用方法进行了详细的描述；2015年梁聪刚、王鸿章[9]对供应链与排序问题在动态规划的背景下进行研究；2014年潘云涛[6]将动态规划与公共设施管理联系在一起进行研究.2015年程六满、王柯敬[11]阐述了各行各业的企业都在管理应用中加入取得到了广泛的应用.常淑芬[7]通过实际管理中的一些例子来阐述动态规划在管理中的应用.而Mitten则提出的一些基础性观点后来也被应用在动态规划的发展当中，并对显式动态规划路径的数学性质做出了很大的贡献.

2 基本原理

一个过程的最优策略具有这样的性质，即无论其初始状态及其初始策略如何，其以后诸决策对以第一个决策所形成的状态作为初始状态而言，必须构成最优策略[4,5].

基本步骤：

(1)将问题的求解过程恰当地分成若干阶段，一段可按问题所处的空间或时间进行分，并确定阶段变量，对n个阶段问题(k=1,2,...,n);

(2)正确地选择状态变量sk，它应当满足无后效性等三个条件，并确定状态集合sk;

(3)确定决策变量xk及阶段的允许决策集合Dk(sk);

(4)写出状态转移函数sk+1=Tk(sk,xk);

(5)由已知条件，得到指标函数Fk,n,fk(sk),F1,n,f1(s1)由最优化原理，列出

fk(sk)={Fk,n(sk)}=min{d(sk,xk)+fk+1,n(sk+1)}.

于是得基本方程

也称为逆序法递推公式.

3 模型求解

3.1 逆序解法

由于查找最优解优方向与多阶段决策过程的实际进行方向相反，从最后一段开始计算逐段前推，求得全过程的最优策略.

解：令第k阶段初已有的状态变量sk是分配给第k到第三个项目的金额；决策变量yk为投第k个项目的资金；状态转移方程为sk+1=sk-yk.初始状态为sk时，从第k到第三个项目的利润最大，第k阶段的最优指标函数用gk(sk)表示，那么g1(s1)为所计算的总利润.

递推方程为：

k=3时，

k=2时，

设

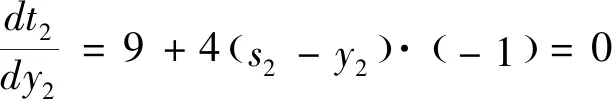
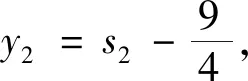
当k=1时，

g2(s2)=9s2时，

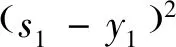
其次，稳定供需关系，健全天然气需求管理。建立天然气发展综合协调机制，推动供用气企业全面签订合同，鼓励签订中长期的供气合同。“煤改气”坚持以气定改，在落实气源的前提下有规划的推进。突出京津冀及周边重点区域，同时建立和完善天然气领域信用体系，对严重违法失信行为实施联合惩戒，健全天然气供需侧管理，准确预测天然气需求。

因此，最优方案于投资第三个项目，最大利润为200万元.

3.2 顺序解法

寻优方向与过程的行进方向相同，计算时从第一段开始逐段向后递推，计算后一阶段要用到前一段的求优结果，最后一段计算的结果是全过程的最优结果.

解：设第1到第k个项目投入的资金用状态变量sk+1,那么s4=10,s3=s4-y3,s2=s3-y2.即状态转移方程：sk=sk+1-yk,令第k段投入的资金sk+1用最优指标函数gk(sk+1)表示，当投入的资金sk+1时，获得第1到第k项目的最大利润，故可得基本方程为：

因此，最优解与逆序法是相同的，该公司只投资于第三项时才获得最大利润200元.

4 应用举例

4.1 资源分配中的应用

例3.M集团有5个新设备，将分配给下属的三个分公司机构，利润如表1所示.那么，该集团如何分配设备以实现总利润最大化.

表1 设备台数及利润的关系

分析：管理的目标是在最小成本下实现最大利润，如何获得有限资源的最优配置是项目投资中要考虑的问题.

解：

(1)建立数学模型

令第i个分公司收到xi设备后得到的收益用目标函数Ti表示，分配给第i个分公司的设备总数用决策变量xi表示，那么

设备分配给第k个分公司的过程为第k个阶(k=1,2,3),状态变量sk为分配给第k个分公司的设备总数,0≤sk≤5,决策变量xk为分配给第k个分公司的设备数,0≤xk≤sk,状态转移方程：

第k个分公司接受xk设备后得到的收益用阶段目标函数Tk(sk,xk)表示，将设备sk分配给第k个分公司到第n个分公司后到的总收益用最优指标函数gk(xk)表示.从而动态规划的基本方程为：

(2)递序法求解

变量sk=0,1,…,5,xk=0,1,…,5,k=0,1,…,5.

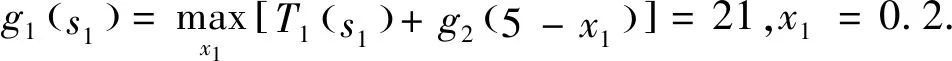
(3)结论分析

求解得出最大利润g1(s1)，然后按k=1,k=2,k=3.递推，从而得出最优策略有两种方案：x1=0,x2=2,x3=3或x1=1,x2=2,x3=1.得到的结果可知，第三个分公司1台，分配给第二个和第三个分公司2台，或分配第一个分公司0台，第二个分公司2台设备，第三个分公司3台设备或分配给第一个分公司2台，该集团的利润和为21万元.

4.2 采购与销售问题中的应用

例4.服装城使用仓库来专门销售一种产品.仓库的最大容量可以储存1000单位的货物.如果服装城每个月只能销售仓库月的货物.该服装城在某月进货时，货物下月初能到，甲商品四个月的买卖价格如表2所示，若服装城自一月销售以来，仓库有商品500单位.该服装城如何计划一月至四月的进购与销售，若不算库存成本，使预期收益最大.

表2 买卖价格表

解：(1)变量说明

状态变量sk：第k月初仓库中的存货量；决策变量xk：第k月卖出的货物数量；决策变量yk：第k月订购的货物数量；状态转移方程:sk+1=sk+yk-xk;最优指标函数fk(sk):从第k月到4月末所获得的最大收益.则有以下逆序递推关系式：

(2)问题求解

x3=s3,y3=1000时,有最大值，f3(s3)=60000+13s3;

得x2=0,y2=10000-s2,f2(s2)=6000+13s2+4000-4x2=10000+9s2;

得x1=500,y1=0,f1(500)=14500+3×500=16000.

表3 最优策略表

(3)结论分析：第一月订购的货物数量为0.卖出的货物数量为500时，则由逆序递推得出最大利润为16000.

4.3 生产管理中的应用

例5.时代设计公司一个机器设计出两种不同价格产品的模型，机器一天内可利用8小时，设计两种模型的任意一种都要占机器1小时，令两种模型售价与产量成线性关系.(10-s1)与(14-2s2)为该两种产品的销售价格，而s1,s2分别为两种产品模型的产量,设两种产品的成本分别为2s1和4s2,如何安排两种产品模型的生产量才能使该电脑在8小时内获收益最大.

解：(1)问题分析：令y1是电脑可利用的，即s1=8,y2是生产第一种产品s1件后剩余的可利用的电脑时间，y3是生产第二种产品s2件后电脑可利用的时间.

(2)建立模型:因要求电脑用8小时，所y3=0.于是状态方程为：

由状态方程y2=y1-s1代入上式得：

由此得到最优策略生产第一种产品模型5件，第二种产品模型3件，8小时可获收益27百元.

4.4 设备更新中的应用

例6.全自动洗衣机的平均一年的更新净费以及维修费用、效益表4所示，如何在接下来五年内制定更新战略，以实现总利润最大化.

表4 更新净费和维修费、效益用表

解：当k=5时，状态变量r5可取1,2,3,4

当k=4时，状态变量r4可取 1,2,3,

当k=3时，状态变量r3可取1,2,

当k=2时，状态变量r3只取1,

当k=1时，状态变量r3只取0，

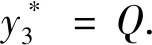
所以最优策略为:{K,Q,Q,Q,K},即第一年初购买的全自动洗衣机到第2、3、4初各更新一次，可用到第5年末，总利润为17千元.

5 结论

通过对动态规划在管理等方面的应用得知，利用动态规划解决某些多阶段决策问题，它的思路清晰、简单、容易实现.在一般情况下，将一个大问题拆分成若干个小问题时，利用数学算法的方式找到解决每一个分问题的最优方法，从而解决一些较大的问题.若在管理的工作中融入动态规划的思想方法，可以为企业的销售管理、生产管理、经营管理、资源分配等领域的发展提供有效决策，并且为企业规划人员、处理数据和监督检查等部署业务做出合理的判断和分析，更新管理方法和优化企业管理手段，从而提高企业经营各个环节的效率和应变能力，实现企业经济效益增长，就会给企业的管理工作带来极大的方便.