带粘性含不活泼项Cahn-Hilliard 方程解的存在性
徐红梅,王一平
(河海大学理学院,江苏南京211100)
1 简介
带粘性的含不活泼项Cahn-Hilliard 方程柯西问题形式如下:

此处n 是空间维数, n ≥1; 未知函数u 表示一个相的相对浓度; 非线性项∆f(u) 中f(u) 取成u2. (1.1) 式中若去掉utt−∆∂tu, 方程为

(1.2) 式是著名的Cahn-Hilliard 方程[1]. 近年来, Galenko 等[2−5]为模拟在某些玻璃中有深过冷产生的非平衡分解提出在(1.2) 式中加上不活泼项utt, 得

(1.3) 式详细的物理背景可参看文献[4–6]. (1.3) 式是一个带松弛项的双曲方程, 它在有限的时间内的不正则化导致很难得到其解的整体存在性. 对(1.3) 式, 前面的工作主要集中在弱解和拟强解. 如Grasselli 等[7,8]得到2 维和3 维情况下拟强解的存在性; Wang 和Wu[9]得到(1.3) 式在n ≥3 时小初值情况下经典解的存在性. 为克服不正则化困难, 在数学上经常是对方程加一粘性项, 增加耗散性, 如是得到(1.1) 式. 本文考虑(1.1) 式解的整体存在性.
本文中用C 表示常数, Lp(Rn), Hl(Rn) 表示通用的龙贝格可测函数空间和Sobolev 空间, 其模为
本文先分析(1.1) 式的格林函数, 再用压缩映像原理证明(1.1) 式解的整体存在性.
2 格林函数分析
定义函数f 关于变量x 的傅里叶变换为


方程(1.1) 格林函数定义如下:
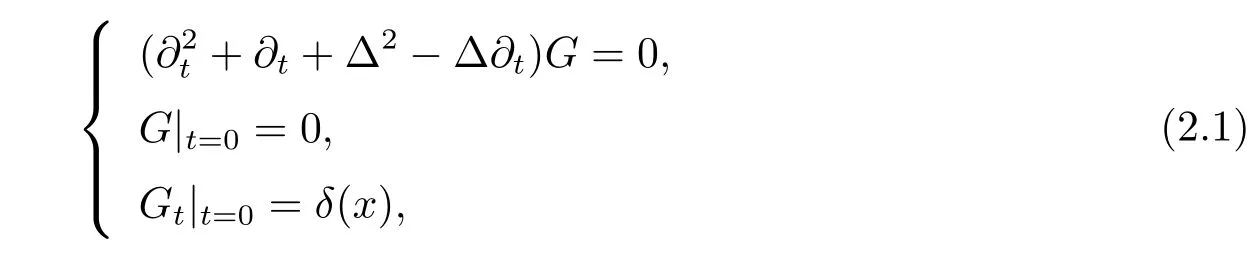
其中δ(x) 为常用Dirac 函数. 对(2.1) 式关于变量x 作傅里叶变换, 得常微分方程

(2.2) 式的解为

其中

由(2.4) 式可知

当|ξ|2<1 时, 有
对于两组患者的并发症进行比较,观察组患者出现皮下气肿患者1例,出现腹部感染患者0例,出现泌尿系统感染患者2例,并发症发生率为11.11%,对照组患者出现皮下气肿,患者4例,出现腹部感染,患者3例,出现泌尿系统感染5例,患者并发症发生率为44.44%,两组之间比较差异明显,P<0.05,具有统计学意义。



其中a>0. 当|ξ|2>1+ε 时,

由以上分析得到下述定理.
定理2.1对任意多重指标α, 存在常数Cα, 有

证由Plancherel 等式,

由(2.5) 式,

由(2.6) 式,

由(2.9) 式,

由(2.7), (2.8) 式得

因为

下面将由不动点定理证明(1.1) 解的存在性.
3 解的整体存在性
令

其中∗是对变量x 的卷积.
定理3.1T 是从X 到X 的压缩映射.
证由定理2.1, 当|α|≤1, 有
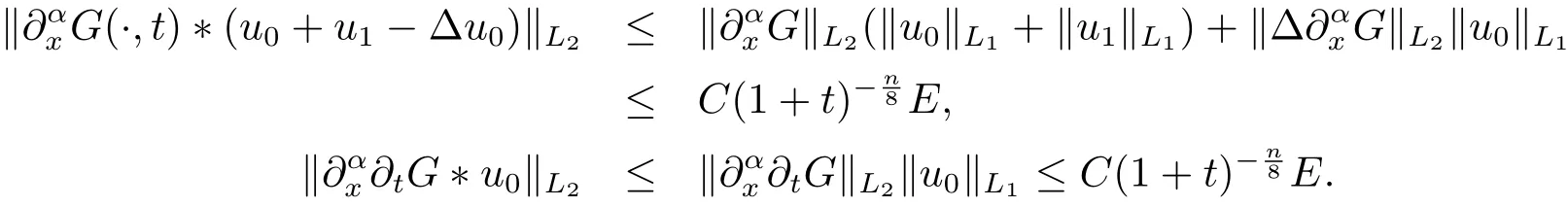
由定理2.1, Minkowski 不等式及f(u)=u2, 当|α|≤1, 有


因为方程(1.1) 的解为u=T(u), X 又为完备度量空间, 于是得到本文结论.
定理3.2若u0,u1∈L1(Rn),则方程(1.1)有整体经典解存在,且u ∈L∞(0,+∞;H1(Rn)),
- 数学杂志的其它文章
- MULTIPLICITY OF POSITIVE SOLUTIONS FOR QUASI-LINEAR ELLIPTIC EQUATIONS INVOLVING CONCAVE-CONVEX NONLINEARITY AND SOBOLEV-HARDY TERM
- A 2-DIMENSIONAL ANALOGUE OF S´ARKöZY’S THEOREM IN FUNCTION FIELDS
- LAZY 2-COCYCLE ON RADFORD BIPRODUCT HOM-HOPF ALGEBRA
- AN ESTIMATE FOR MAXIMAL BOCHNER-RIESZ MEANS ON MUSIELAK-ORLICZ HARDY SPACES
- PROBABILITY INEQUALITIES AND ROSENTHAL INEQUALITIES FOR THE SEQUENCE OF MARTINGALE DIFFERENCES
- 非一致分布下的在线分位数回归算法

