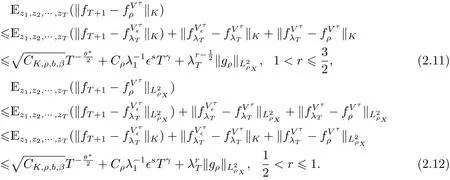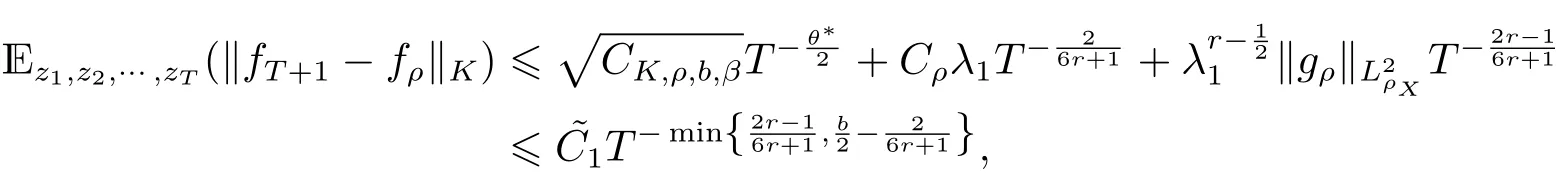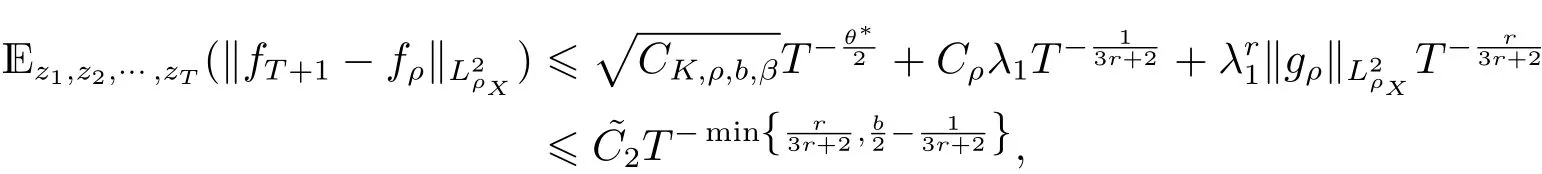非一致分布下的在线分位数回归算法

杨鹏伟

(武汉大学数学与统计学院, 湖北武汉 430072)

1 引言

1.1 不同分布下的样本

假设输入空间(X,d)是Rn中的紧度量空间, 输出空间Y ⊂R, 样本空间Z = X ×Y.非一致分布下, 每一学习时刻t = 1,2,··· 产生的样本点zt= (xt,yt) ∈Z 服从联合概率分布ρ(t)(x,y), (x,y) ∈Z, 这里序列不一定相同. 在Smale, Zhou[1]提出的学习框架下, 假设在X 上的边缘分布序列以多项式速度收敛于Hölder 空间Cs(X)(0

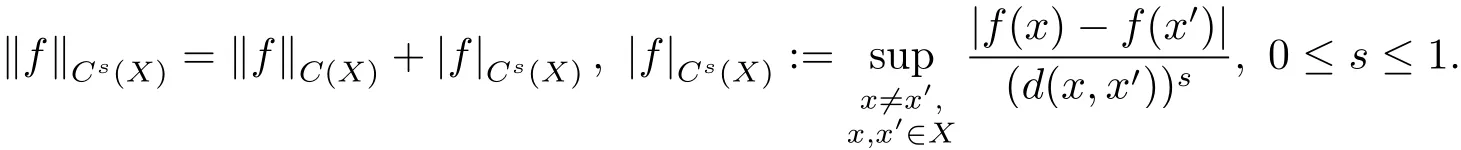
定义1.1称概率分布序列以多项式速度收敛于(Cs(X))∗中的概率分布ρX. 如果存在C >0,b>0 使得

由对偶空间(Cs(X))∗的定义, 条件(1.1)等价于

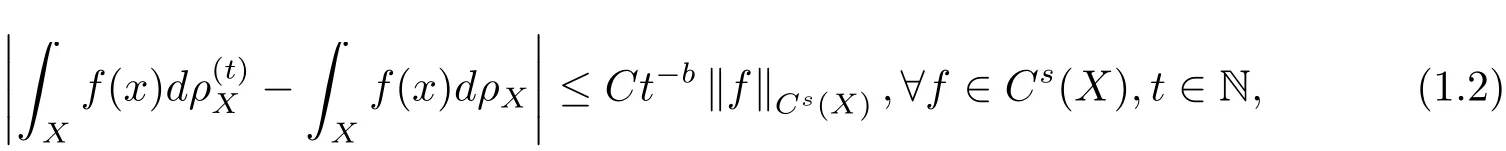
指数b 衡量不同分布的差异程度, 当b=∞时, 条件(1.1)是独立同分布.

对于满足衰减条件(1.1)的实际情况已在文献[1, 3]有详细讨论. 例如, 真实的抽样分布ρX被噪声干扰并且随着时间t 增加而噪声水平下降, 那么在不同时刻对应的抽样概率分布收敛于ρX. 另外, 通过迭代和随机密度核形成的积分算子, 反映了由动力系统诱导出不同分布的表现形式. 这些例子都说明研究满足(1.1)衰减的分布是具有实际应用性的.

1.2 分位数回归

对于任意的0<τ <1, 定义随机变量Y 的τ 分位数函数Q(τ)为

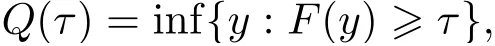
其中F(y)是Y 的分布函数. Koenker, Bassett[4]提出线性分位数回归理论, 扩展了经典的最小二乘回归. Koenker[5]进一步提出分位数回归可提供更多关于因变量的分布信息, 例如: 长尾性、厚尾性、多峰性. 分位数回归描述因变量的条件分布, 不仅仅分析因变量的条件期望,并且对不同τ 刻画了概率分布的具体性质.

在学习理论框架下, ρ 是Z 上的一个Borel 概率测度. 给定x ∈X 时, ρx(y),y ∈Y 是ρ的条件概率分布. 分位数回归的目标函数fρ,τ(x)在x 的值定义为: ρx(·)的τ - 分位数是v,即存在v ∈Y 满足

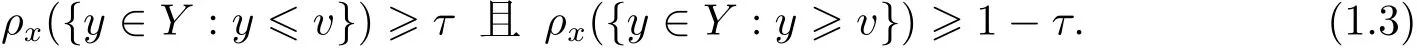
1.3 在线分位数回归算法

再生核Hilbert 空间(RKHS)是由Mercer 核K :X×X →R 诱导出来的,K 是一个连续对称函数,并且对于任意有限点集{x1,x2,··· ,xl}⊂X 生成的矩阵是半正定的. 由函数集{Kx=K(x,·):x ∈X}张成的完备线性闭包空间RKHS 记为HK(Aronszajn,1950[7]),记内积为= K(x,y). 在线算法也称随机梯度下降算法(SGD) 与批次算法中样本一次性传给机器不同, 在线算法的训练样本是按时间t 顺序依次传送给机器, 对算法不断修正, 提高学习效率. 在线算法由于低复杂度, 在流式数据和大规模计算中有广泛的应用. 具体可参考文献[8].

定义1.2与RKHS 有关的在线分位数回归算法定义为

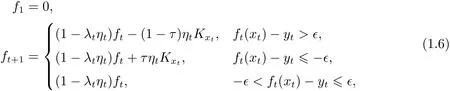
其中t 是学习时间, λt>0 称为正则参数, ηt>0 是步长.

在线算法(1.6)中, 正则参数λt随着学习时间t 变化并且当λt≡λ1时, λt不会随着步数t 变化而变化, 此时称(1.6)为不完全在线算法.

2 非一致分布下在线分位数回归的误差

高斯函数在统计学领域, 用于表述正态分布; 在信号处理领域, 用于定义高斯滤波器; 在图像处理领域, 二维高斯核函数常用于高斯模糊; 在数学领域, 主要是用于解决热力方程和扩散方程. 高斯核函数作为最常用的径向基函数, 在支持向量机等算法中的应用可以将数据映射到高维甚至无穷维. 由于高斯核具有良好的性质和应用广泛, 因此将高斯核应用于以下与中位数回归有关的在线算法(1.6)中.

对于f :X →R 的泛化误差定义为

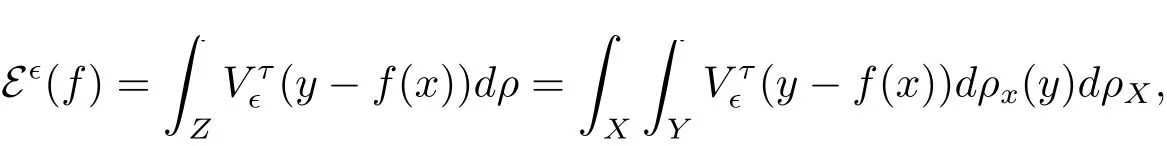
定理2.1假设以下假设均成立

1. RKHS HK由高斯函数产生;

5. ∀x ∈X, 条件分布ρx(·)是区间[fρ(x)−1,fρ(x)+1]上的一致分布.

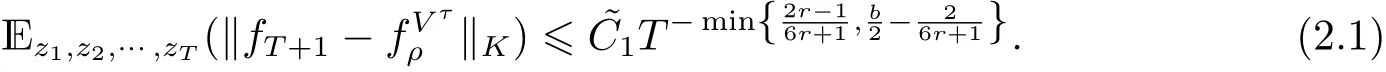
注1该定理反应了中位数回归的在线算法收敛速度, (2.1)式说明了在线算法(1.6)在HK的收敛性, 称为强收敛; 而结果(2.2)称为算法的平均误差. 由范数关系知道本定理结果(2.1)和(2.2)是合理的. 虽然本定理是考虑τ =, 但是从后面的证明过程知道本定理结果可以推广到任意0<τ <1, 只需要修改常数˜C1和˜C2.

注2在线算法(1.6)的误差估计分为抽样误差和逼近误差两部分, 其中抽样误差是本文的主要贡献, 将在定理2.3 中给出; 逼近误差由HK空间的复杂度和数据的分布ρ 决定. 假设5 采用一致分布估计逼近误差. 事实上本定理适用于其他更一般的条件分布, 为了简化本定理, 不再进一步讨论. 具体可参考文献[2, 3].

注3当b=∞, (2.1)和(2.2)式反映了数据抽样z是独立同分布的情况. 另外, 我们看到时, 本定理推导出无稀疏性的在线分位数回归算法的收敛阶, 可以通过调节的值控制算法的稀疏性同时不影响算法的收敛率.

2.1 抽样误差的估计

定义2.2对于λ>0, 正则化函数定义为

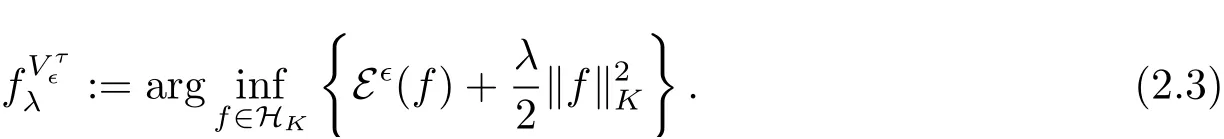
逼近误差D(λ)定义为

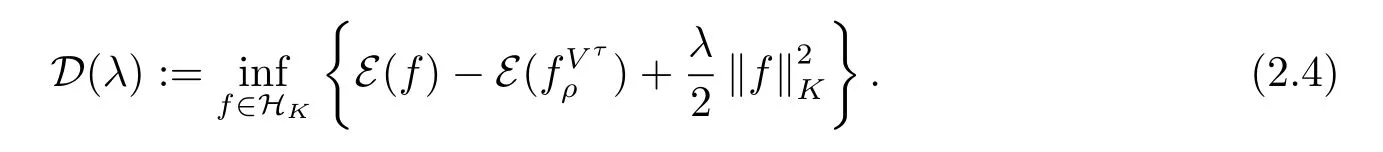
定理2.3如果以下假设成立

1. 核函数K 与定理2.1 相同;

3. 分布{ρx:x ∈X}在(Cs(X))∗中是Lipschitz s 的, 即存在一个常数使得

4. 逼近误差满足多项式衰减如下

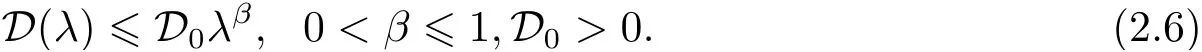
令

则有

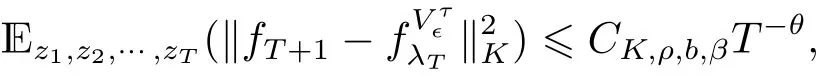
其中

CK,ρ,b,β是独立于T 的一个常数且在证明中给出.

证本定理的证明借助了Hu,Zhou[3]的证明思想. 以下给出证明的主要步骤, 更详细的过程参见Hu,Zhou[3]的定理26. 证明分为三个步骤.

第一步存在常数κ2s>0,

由K(x,x)=K(u,u)=1, 得

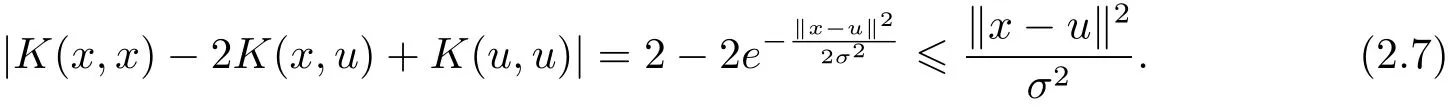
第二步由Ying,Zhou[8]引理3 知

其中

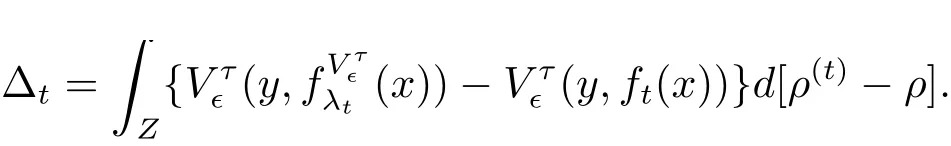
因此需要估计∆t的上界(参考文献[3] ). 不难证明存在常数使得. 根据关于第二变量的一阶Taylor 展开, 可知

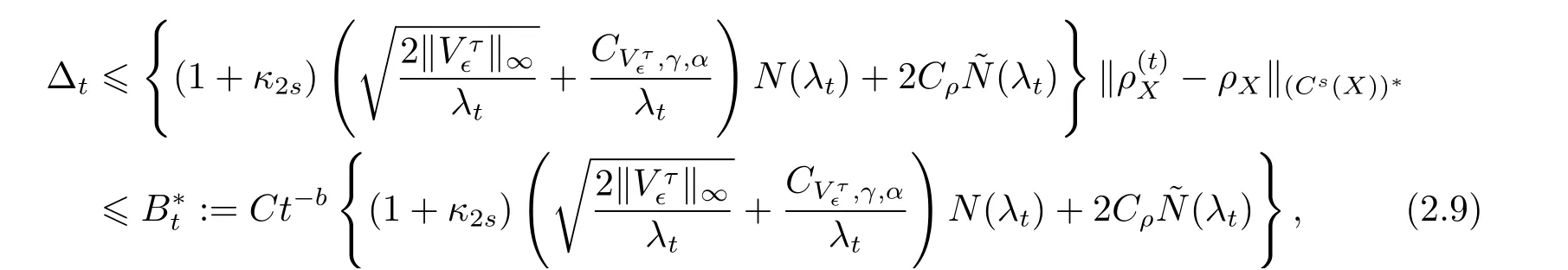
这里

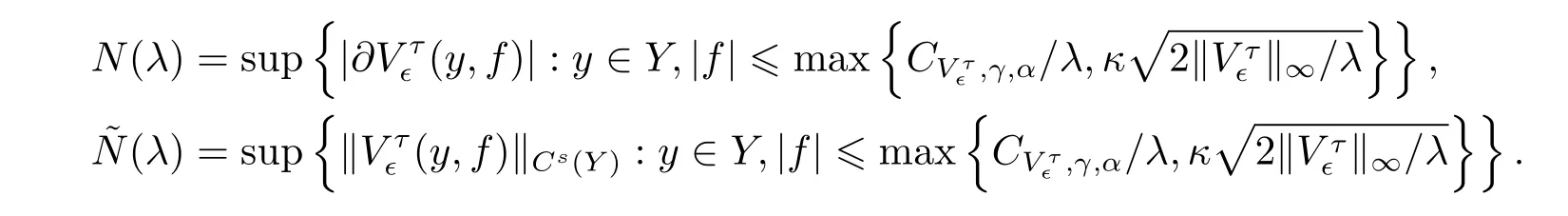
将估计(2.9)式代入(2.8)式得

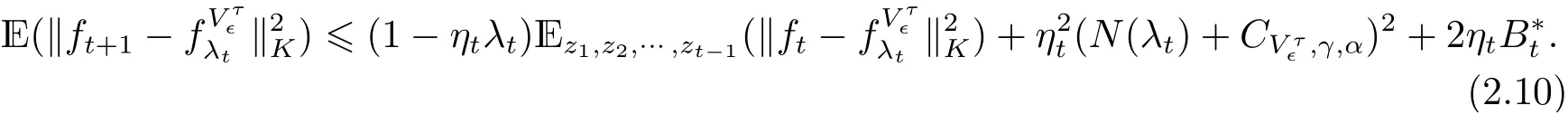
第三步根据, 知必然存在常数使得同时,注意到当, 可以引用文献[9] 中引理3(b), 得到

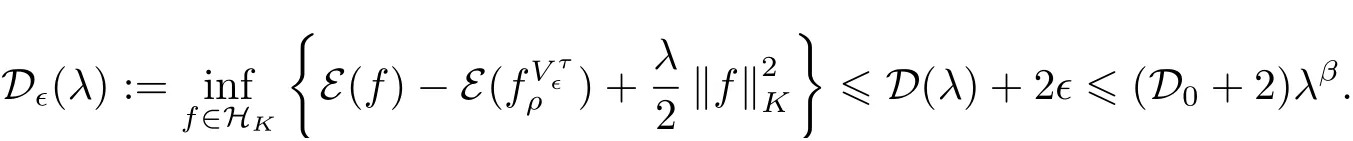
所以用文献[3] 定理20 的结果, 得到

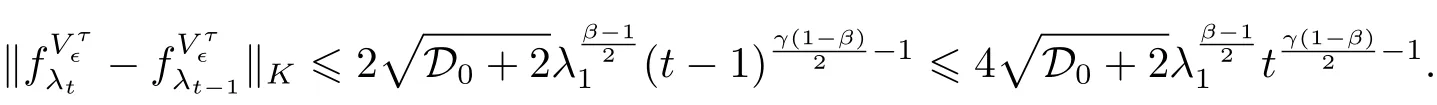
将上述估计插入(2.10)式, 并按t=T,··· ,1 顺序进行迭代, 得到本定理结论.

2.2 定理2.1 的证明

证将误差分解为三项:

首先, 根据条件5 和在文献[10]例6 知道, 在正则条件下

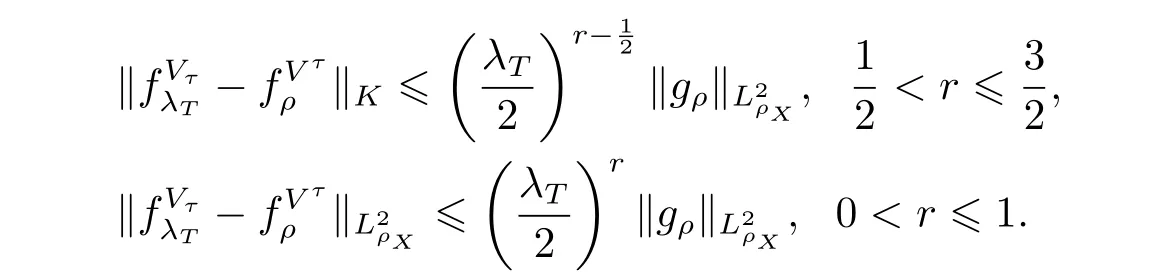
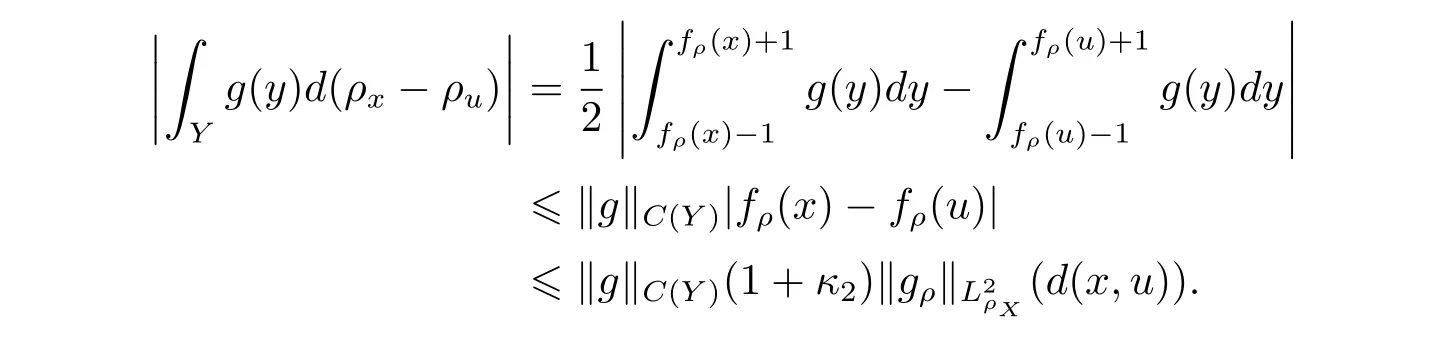
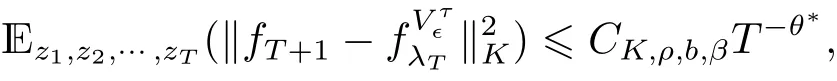
这里θ∗:=min{2 −2γ −2α,α −γ,b −2γ}.

根据以上推导得到