基于Park模型对海上风电场尾流的敏感性分析

陶英佳，黄小祥，周辉

基于Park模型对海上风电场尾流的敏感性分析

陶英佳，黄小祥，周辉

（上海勘测设计研究院有限公司，上海 200062）

尾流的计算直接影响风电场发电量的估算结果及项目财务指标，基于Park模型对某海上风电场的尾流计算结果做敏感性分析，结果表明，尾流损失随着值的变化呈现出二次函数的相关变化，随着值的升高，尾流降低幅度越来越小；尾流损失随着风速的变化呈现出线性函数的相关变化，随着风速的提高，尾流也相应地呈线性降低。

Park模型；尾流；海上风电场；风机

风经过风力发电机后，由于叶轮吸收了部分风能，风力发电机的下游风速出现一定程度的突变减小，而后又逐渐恢复。在风电场中，多台风机间的尾流叠加又会影响其他受影响风机的工作风速，进而影响其他风机出力，导致全场的实际发电功率总是低于理论发电功率。

由于海面的粗糙度较小、湍流强度低，风电机组尾流的影响距离较远。此外，海上风电场工程装机容量较大，多台风机间的尾流叠加影响较大，因此，陆上风电经验得到的尾流模型应用在海上风电场时，往往会低估尾流的影响[1]。尾流的计算直接影响风电场发电量的估算结果及项目财务指标，并影响项目前期投资方对项目的投资决策。综上，在海上风电项目设计过程中，对风电场尾流的研究显得尤为重要。本文基于Park模型对某海上风电场的尾流计算结果做敏感性分析。

1 Park模型

描述风电场风机尾流的数学模型有多种，比如一维线性尾流模型、二维轴对称涡粘模型、三维流体计算软件仿真模型等。其中，最经典且最常在工程项目中使用的两类尾流数学模型分别是Park模型（一维线性模型）和Eddy模型（二维轴对称涡粘模型）[2]。Park模型模型由丹麦Riso可再生能源实验室的Katic等人提出，目前已被广泛应用于风能行业的风能资源评估及发电量测算软件中，该模型基于完成解析的数学表达式，拥有计算量低、响应速度快、参数调整灵活等特点。

Park尾流模型的原理为：假定气流经过风机叶轮后所形成的尾流沿风机中心线呈轴对称形态，并且尾流宽度随着下风方向距离的增加而呈线性增加，但速度衰减逐渐恢复。

如果一台风力发电机的叶轮部分位于另一台风力发电机的尾流区域中，风速衰减是与两台风力发电机的叶轮重叠面积成比例：

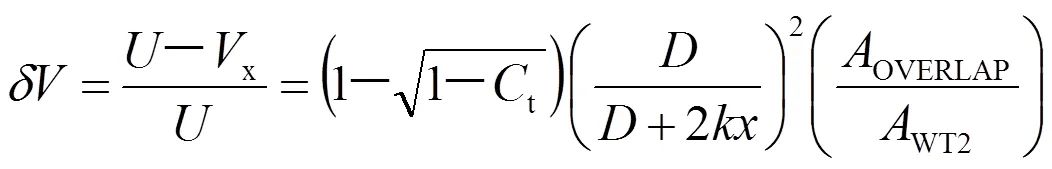
式（1）中：t为风机推力系数；为风机直径；OVERLAP为叶轮重叠面积；WT2为下游风机叶轮面积。

2 风电场概况

风电场离岸距离约20 km，水深在20 m以上，场址面积约80 km2，拟规划采用73台单机容量为5.5 MW的风力发电机组，风电机组布置呈三角形形状，一共布置五排风力发电机组，风电场布置及各个风机编号如图1所示。采用5.5 MW风机标准空气密度下的功率曲线和推力系数t值，作为计算输入。根据上述输入条件，值取0.05的情况下，本风电场平均尾流损失为10.07%，由于后排受前排尾流叠加的影响，57号机位单机尾流最大，最大单机尾流损失达到了14.71%。

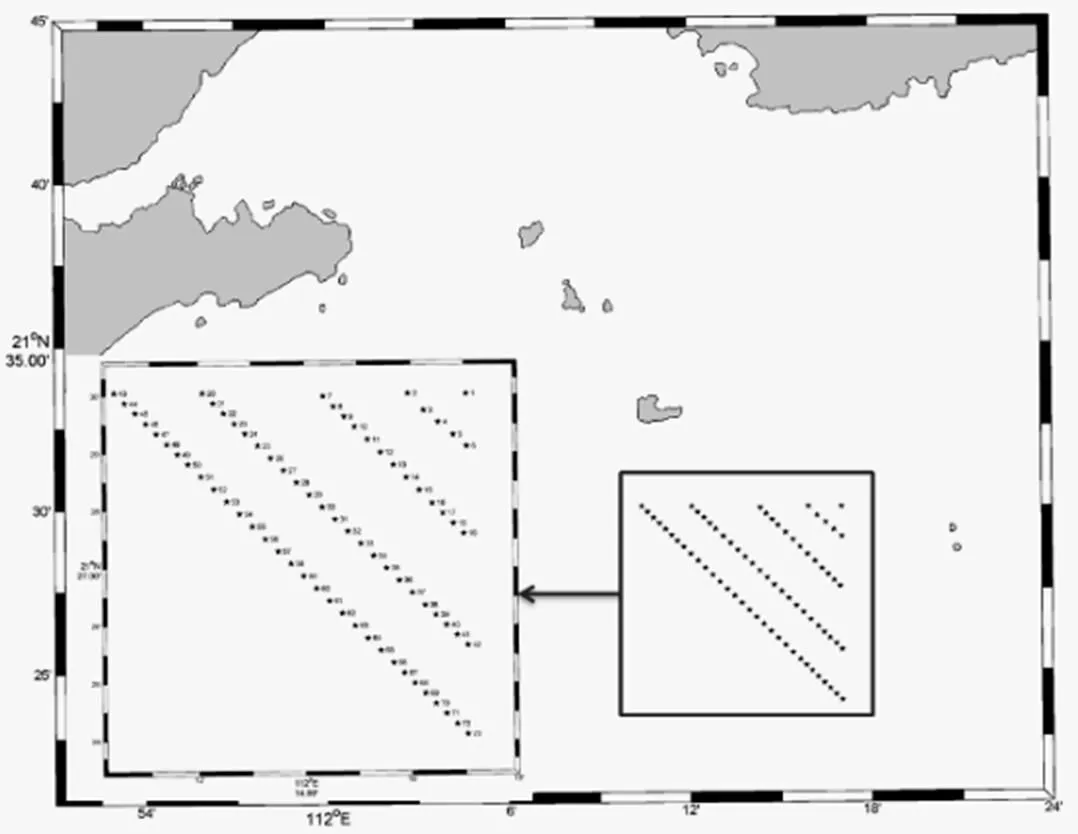
图1 风电场场址示意图

3 尾流敏感性分析

在风电场所选用机型和机型布置明确的情况下，采用Park模型计算得到的风电场尾流主要取决于风电场风资源评价结论和模型中参数的选取。Park模型的核心在于通过定义尾流衰减因子来表示尾流的线性扩张。尾流衰减因子与环境湍流及地面粗糙度相关。通常随着环境湍流强度的增加而增大，常用取值为0.03～0.08。的取值不同会直接影响尾流损失与全场发电量计算结果。

风电场风资源评价结论需根据代表气象站多年资料进行长年订正后得到，因此根据测风塔数据直接进行发电量计算存在一定不确定性。

综上，本文主要从风速和值两个方面对风电场的尾流进行敏感性分析。在值取0.05的情况下，通过将各个扇区的风速均提高2%～10%对尾流计算结果进行敏感性分析；在风资源成果不变的情况下，通过调整值对尾流计算结果进行敏感性分析，调整区间为0.03～0.08。

尾流计算结果如表1所示，值变化与尾流损失之间的拟合成果如图2（a），风速提高比例变化与尾流损失之间的拟合成果如图2（b）。根据图表结果可以发现，在风速一定的情况下，平均尾流损失和最大单机尾流损失随着值的变化呈现出二次函数的相关变化，随着值的升高，尾流降低幅度越来越小；在值一定的情况下，平均尾流损失和最大单机尾流损失随着风速的变化呈现出线性函数的相关变化，随着风速的提高，尾流也相应地呈线性降低。

表1 尾流损失随值、风速变化表

K值平均尾流/（%）最大尾流/（%）风速提高比例/（%）平均尾流/（%）最大尾流/（%） 0.0312.3618.94010.0714.7 0.0411.0716.5629.8014.2 0.0510.0714.7149.5213.7 0.069.2713.2669.2413.2 0.078.6112.1488.9612.7 0.088.0311.23108.6612.2

4 结语

本文介绍了Park模型计算尾流的原理，并简单介绍了试验风电场，通过对风电场尾流的计算进行敏感性分析，结果表明，在风速一定的情况下，平均尾流损失和最大单机尾流损失随着值的变化呈现出二次函数的相关变化，随着值的升高，尾流降低幅度越来越小；在值一定的情况下，平均尾流损失和最大单机尾流损失随着风速的变化呈现出线性函数的相关变化，随着风速的提高，尾流也相应地呈线性降低。

［1］程海锋，胡志坚.海上风电场风电机组的尾流控制［J］.水利规划与设计，2013（12）：94-97.

［2］郑爱玲，梁中荣.大型海上风电场尾流损失计算方法对比［J］.风能，2016（1）：84-86.

TM614

A

10.15913/j.cnki.kjycx.2019.17.015

2095－6835（2019）17－0036－02

〔编辑：张思楠〕