某微车驱动桥模态分析

胡礼，吴小东，陈海，郝锌，孙伟元，李永放，陈志洋

（四川建安工业有限责任公司，四川 雅安 625000）

前言

随着中国经济的高速发展，市场竞争日益激烈，人们对整车的要求也越来越高，这不得不要求整车厂以最低的成本在最短的时间内推出质量最好的产品。驱动桥作为微车最为重要的结构传动部件，极其影响整车的安全性、舒适性和稳定性，所以设计的好坏将直接决定产品在市场上的声誉。

本文以某微车驱动桥为例，通过在Hypermesh14.0 里进行网格划分，然后用ABAQUS 进对某微车驱动桥进行模态分析，以确定改进后的结构方案是否能够改善模态频率，以达到提升NVH 性能的目的，为微车驱动桥提供噪声振动有效的解决方案，也为以后同类产品的研发提供设计参考。

1 有限元模型建立

由于驱动桥的连接件比较多，通过几何模型的简化处理，建立的有限元模型如下：

图1 驱动桥原模型（中段短）

图2 驱动桥新模型（中段长）

1.1 材料参数

为了以上两个模型计算对比方便，现将材料参数统一要求如下：

弹性模量：210Gpa；

泊松比：0.28；

密度：7.9×103Kg/m3。

1.2 分析方法

运用ABAQUS 的模态分析方法，可以考察驱动桥结构对整车NVH 的影响，从而避免出现共振的情况。在ABAQUS中，一共有三种计算模态固有频率和振型的方法，分别是：自动多层次子结构方法（AMS method）、子空间法 （Subspace method）、兰索士法（Lamczos method）。这三种解法各有用处，需要根据模型的实际情况进行选择。比较而言，兰索士法首先推荐的。

兰索士（Lanczos）法是一种将跟踪法和变换组合起来的新的特征值解法，对计算非常大的稀疏矩阵几个特征值问题最有效，特别是当模型的规模比较大时，且需要提取多阶振型时，兰索士的方法速度更快。本文采用的是Lanczos 法计算驱动桥的前12 阶模态。

1.3 分析目标

根据某主机厂要求，该驱动桥的一阶弯曲的固有频率大于100Hz。

2 模态分析

本文中模态分析为自由模态分析，前六阶为刚体模态，频率全部为0，故不进行考察。只考察除去前六阶刚体模态的后面6 阶模态情况。

2.1 模态频率

表1 模态分析结果

2.2 模态振型

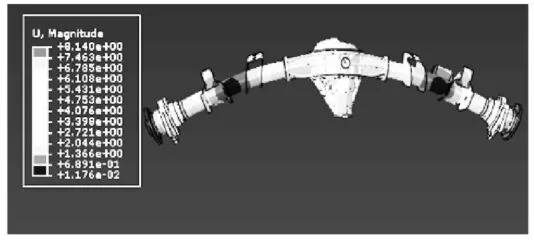
图3 一阶（原模型）

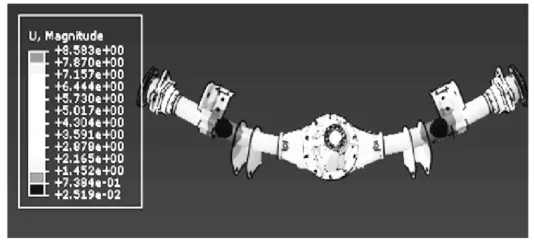
图4 二阶（原模型）

图5 一阶（新模型）

图6 二阶（新模型）

2.3 NVH 测试

通过对4，5 档加速时NVH 性能的表现可以看出，新模型中段在原模型基础上增加了50mm 后，最大噪声峰值降低了约10db，NVH 性能得到了大幅度改善。

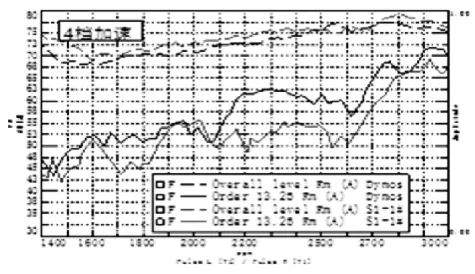
图7 四挡加速噪声

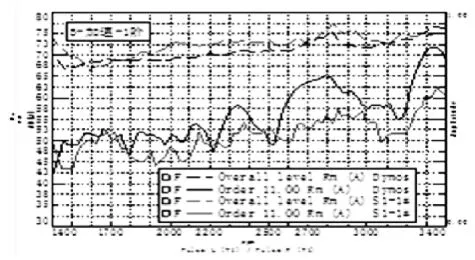
图8 五档加速噪声

2.4 分析比较

从上面的分析结果对比来看，新模型中段在原模型基础上增加了50mm 后，模态频率有所提升，第一阶弯曲频率达到了101HZ，满足设计要求；从NVH 测试结果来看，最大噪声峰值降低了约10db，NVH 性能得到了大幅度改善。

3 结论

本文通过对某微车驱动桥进行模态分析，得出新模型中段在原模型基础上增加了50mm 后，模态频率有所提升，第一阶弯曲频率达到了101HZ，能够满足设计要求，同时NVH性能得到了大幅度改善，最大噪声峰值降低了约10db，为以后类似产品开发提供了宝贵的经验。