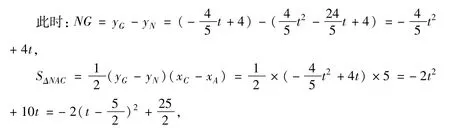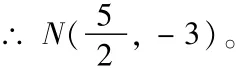掌握一种求三角形面积的公式，巧解中考数学题

秦宇峰

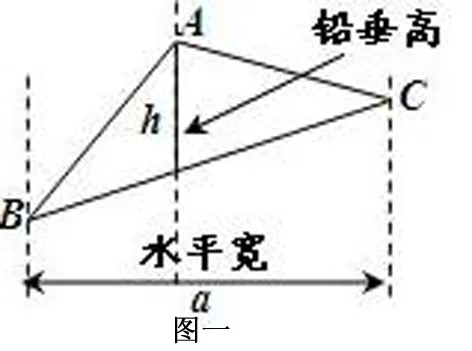
现总结如下：如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”.我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半.

注意事项：

1.找出B、C的坐标，横坐标大减小，即可求出水平宽；

2.求出直线BC的解析式，h与直线BC交于点D，A与D的横坐标相同，A与D的纵坐标大减小，即可求出铅垂高；

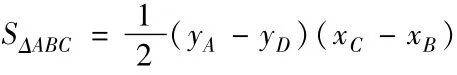
例1.（2014潍坊改编）如图，抛物线y＝ax2+bx+c（a≠O）与y轴交于点C（O，4），与x轴交于点A和点B，其中点A的坐标为（-2，0），抛物线的对称轴x＝1与抛物线交于点D，与直线BC交于点E

（1）求抛物线的解析式；（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；（3）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为16，若存在，求出点F的坐标；若不存在，请说明理由；

（4）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为15，若存在，求出点F的坐标；若不存在，请说明理由。

解：（1）由抛物线经过点C（O，4）可得c＝4，①∵对称轴x＝-＝1，∴b＝-2a，②，

又抛物线过点A（一2，O）∴0＝4a-2b+c，③

令x2+4x+12＝17，即x2-4x+5＝0，则△＝（一4）2-4×5＝一4＜0，

∴方程x2-4x+5＝0无解，故不存在满足条件的点F.

（3）令x2+4x+12＝16，即x2-4x+4＝0，则△＝（一4）2-4×4＝0，

∴方程x2-4x+4＝0有唯一解x＝2，故存在满足条件的点F（2，4）.

（4）令x2+4x+12＝15，即x2-4x+3＝0，则△＝（一4）2-4×3＝4，∴方程x2-4x+3＝0有两个解x1＝1，x2＝3，故存在满足条件的点F1（1，4.5），F2（3，2.5）。

例2（2015·武威改编）如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M.

（1）求抛物线的解析式和对称轴；

（2）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由.

解：（1）根据已知条件可设抛物线的解析式为y＝a（x-1）（x-5），把点A（0，4）代入上式得：

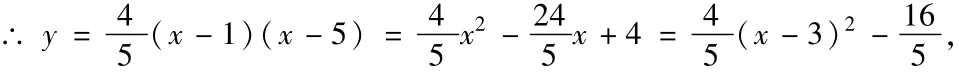
∴抛物线的对称轴是：x＝3；

（3）在直线AC的下方的抛物线上存在点N，使△NAC面积最大.，设N点的横坐标为t，此时点如图2，过点N作NG∥y轴交AC于G，

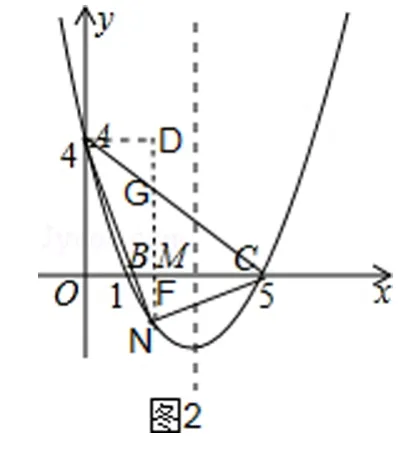
由点A（0，4）和点C（5，0）可求出直线AC的解析式为把x＝t代入得：，则