试析数学学科的小升初衔接问题及对策

杨慧园

本人在深圳市一所区直属的九年一贯制学校的初中部任教多年，直到2017年，学校把六年级纳入初中部进行管理，我因此有机会到六年级任教。六年级作为九年义务教育承上启下的年级，承担着中小衔接的重要任务。下面，就数学学科在小升初的衔接过程中出现的问题，谈谈几点思考，仅供同行探讨。

一、数学学科的小升初衔接问题

1.关注考点教学，衔接意识不足 六年级虽然没有中考、高考的升学压力，但学年度末也有学业水平测试。有的老师为了追求分数，不是考点的内容和题目不讲，怕“浪费”时间。而对于易错点，则想办法教学生规避。

比如，在教授六年级上册《圆的面积》时，该内容要求学生经历探索和推导圆的面积公式S＝πr2的过程。这将为七年级上册《有理数的乘方》和《代数式》的学习打下基础。但是有的老师不仅忽视了让学生体会“S＝πr2”产生的过程、表达的含义和书写注意事项，更有甚者，对于类似“已知圆的半径为3，求圆的面积”的题目，要求学生直接列出“3.14×3×3”的式子，以避免出现“32＝3×2＝6”的错误。这样的教学方法显然不利于学生对于“数到式”的知识衔接的学习。

2.强调技巧训练，忽视思维方法 为了帮助学生快速高效的掌握所学，小学阶段有不少朗朗上口的口诀。比如在学完六年级上册《分数混合运算》之后，不少老师都会教学生用口诀“已知单位1用乘法，求单位1用除法”来解决分数应用问题，这看似无可厚非。但《数学教师教学用书》中在《分数混合运算（三）》的学习目标中明确指出学生应该“会用方程表达分数混合运算问题中的等量关系，并解决相应的的实际问题”。因为“算术式到方程”是中小学数学解决问题方式的本质转变，而方程思想是初中阶段的重要数学思想。

又比如，在《比的应用》这个课时中，已知1班和2班的人数比是3：2，则140个橘子要怎么分？《数学教师教学用书》中指出“方程方法是学生可能出现的方法”，要“鼓励学生独立思考，体验解决问题策略的多样化”。但在教学过程中，有的老师会直接教授容易得分的方法——借助几何直观，用整数乘除或者分数乘法来解决问题，而回避方程解法。这种小学阶段刻意淡化方程方法的做法，剥夺了学生用方程思维解决问题的经验，而方法的固化，也使学生的思维也不够灵活和发散。

3.要求不够规范，学法不够科学

（1）书写的问题。有的老师对学生的书写没有明确要求，于是学生的答题步骤，有的横着写，有的竖着写，有的从中间开始动笔，右边写不下了又拐到左边写，书写样式可谓五花八门。但是学生进入初中后，由于解题过程更复杂，步骤更多，如果没有规范的书写，很容易写成一团乱麻。因此，为了和中学衔接，我们在六年级就可以根据“题号对齐，从上到下，从左到右”的原则来答题，既符合我们的书写习惯，也为将来学习几何证明打好基础，空白部分还可以留作订正，一举多得。

（2）错题本的使用。有的老师没有提醒和要求学生整理错题本，使学生缺少总结反思的意识，缺乏整理错题本的能力。而个别老师则要求学生每天都把作业错题抄在错题本上；有的还要学生先把错误答案抄一遍，再抄正确答案。对于如何整理错题本，虽然没有统一的标准，但是前面提到的这些做法，显然并不够科学。

二、做好数学学科小升初衔接的策略

1.明确学习目标，增强衔接意识 2016年9月13日，教育部公布《中国学生发展核心素养》，正式确定学生发展核心素养的框架、维度和指标。学生发展核心素养是学生在接受相应学段的教育过程中，逐步形成的适应个人终身发展和社会发展需要的必备品格和关键能力。数学，作为中小学教育的主要学科之一，小学教师的教育教学应立足小学，胸怀中学。有条件的学校，特别是九年一贯制的学校，可以加强跨级教研、集体备课，通过阅读课标、教材和教育期刊等科学地制定每节课的学习目标，把握好中小学知识的衔接点。

比如六年级上册《教师教学用书》中《圆的周长》2个课时的学习目标为：（1）结合实例认识圆的周长，在探索圆的周长与直径关系的过程中，理解圆周率的意义及圆周长的计算方法。（2）能正确运用公式计算圆的周长，能运用圆周长的知识解决一些简单的实际问题。这个学习目标的描述对于年轻教师或没有初中教学经验的小学老师来说，并不够具体明确，很难把握到要衔接的点。因此我们可以结合七年级无理数和代数式等知识点，根据学习目标撰写公式：学习目标＝学生+层次动词+学习结果+具体化，把它细化如下：

第1课时学习目标：

（1）能通过滚动、绕线等实例，用自己的语言描述圆的周长。

（2）通过测量和填表的方式探索圆的周长与直径的关系，体会到圆的周长总是直径的3倍多一些（或π倍）。

（3）了解圆周率π≈3.1415926是个无限不循环小数。（这是我们在小学阶段遇到的第一个无理数）

第2课时学习目标：

能利用圆的周长公式C＝πd或C＝2πr，按格式计算圆的周长并解决简单实际问题。格式示例：已知圆的半径为3cm，求圆的周长。

C＝2πr______第1步，写公式。

2×3.14×3______第2步，代入。

＝3.14×6______第3步，根据乘法运算律简化计算。

＝18.84（cm）______第4步，写出答案。

第1步和第3步，在学生熟练运用圆的周长公式后，可以省略。第2步，要跟学生强调，π是一个无限不循环小数，在小学阶段通常取近似值3.14，即π≈3.14，避免学生先入为主，到了初中还误以为π＝3.14。通过学习目标的具体化，我们可以为初中的数域扩充、“数到式”的过渡等衔接做好铺垫。

2.渗透数学思想，到位而不越位 《全日制义务教育数学课程标准（2011版）》将“获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验”确定为课程总标准之一。数学学习的不仅是知识和技能，更重要的是数学思想方法和用数学思维解决问题的能力。在小学阶段，学生的学习多以形象思维和合情推理为主，到了中学，则以逻辑推理为主。因此，小学的数学教学既要注重数学思想的渗透，也要注意把握衔接的度。

比如，六年级下册《圆柱和圆锥》单元测试的一道填空题：一个圆柱和一个圆锥的底面积相等，体积比是6：1，圆柱的高是12cm，则圆锥的高是____cm。

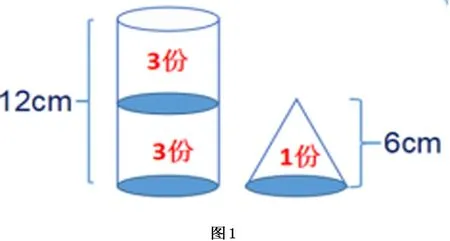
我们应该鼓励学生用数形结合的方法来解决。如图1，因为等底等高的圆柱和圆锥的体积比是3：1，所以把圆锥体积看成1份，那么等底等高的圆柱体积就是3份，而题目说等底不等高的圆柱体积有6份，因此可以看成是2个跟圆锥等底等高的小圆柱组成，从而得到圆锥的高是6cm。但如果用方程方法来解的话，对于六年级的孩子来说反而不容易接受。

3.重视变式训练，培养数学思维 小学阶段的数学新授课的知识点比较单一，往往一节课只需要掌握一个概念、一个原理或者一类题目的解题方法。因此，有部分学生的学习只是模仿老师演示的例题依葫芦画瓢，并不能灵活运用所学。我们在教学的过程中应该注重变式训练，培养学生思维的灵活性和深刻性。

（1）本质不同的对比题组

比如，六年级上册的《分数混合运算》应用题，可以设计以下对比题组：

小明有3元，小白有2元，则小明的钱是小白的几分之几？

小明有3元，小白有2元，则小白的钱是小明的几分之几？

小明有3元，小白有2元，则小明的钱比小白的多几分之几？

④小明有3元，小白有2元，则小白的钱比小明的少几分之几？

（2）本质相同的不同题组

（课本例题）140个橘子，让1班和2班按3：2来分，该怎样分？

（课后练习）一块长方形土地的周长是160m，长和宽的比是5：3，这块长方形的面积是多少平方米？

（单元练习）两辆汽车同时从相距360km的两地相对开出，2.4时后相遇。已知两辆车的速度比是12：13，较慢的一辆车每时行多少千米？

以上三个题都是，已知或先求出两个量的和，再利用这两个量的比求出这个两个量。

4.加强学法指导，提升学习能力 由于中小学生的年龄和思维特点的不同，老师的教学方法和学生的学习习惯也存在一定的差异。小学阶段的知识比较简单，老师经常手把手的教学生，大部分学生对老师有较强的依赖性。因此我们在教学中，要有意识的培养学生的自主学习能力和良好的学习习惯。比如，圈画标注的审题习惯、整洁规范的答题习惯、课前预习、课后整理错题本的习惯等等。另外，还可以通过小组之间的合作竞争、蓝墨云班课和微课小视频等信息技术手段，充分发挥优生对后进生的引领和帮扶作用，营造积极向上的学习氛围，使学生能养成积极思考、主动学习和总结反思的习惯，为初中数学的学习打下良好的基础。