基于蒙特卡罗模拟的误差序列自相关检验研究
叶宗裕,王卫杰
(浙江师范大学 a.经济与管理学院;b.数学与计算机科学学院,浙江 金华 321001)
一、引言及文献综述
由于经济发展的连续性所形成的“惯性”,使得许多经济变量的前后期值之间是相互关联的。经济发展的这种惯性作用,使得利用时序数据建立计量经济模型时经常会遇到“自相关性”的问题,即模型中随机误差项μt的各期值之间存在着较强的相关关系。自相关性的存在将会增大模型系数的估计误差,降低统计检验的可靠性和预测的精度。因此,进行计量经济分析时一般都要检验模型是否存在自相关性,并根据自相关性的类型采取相应的解决方法。
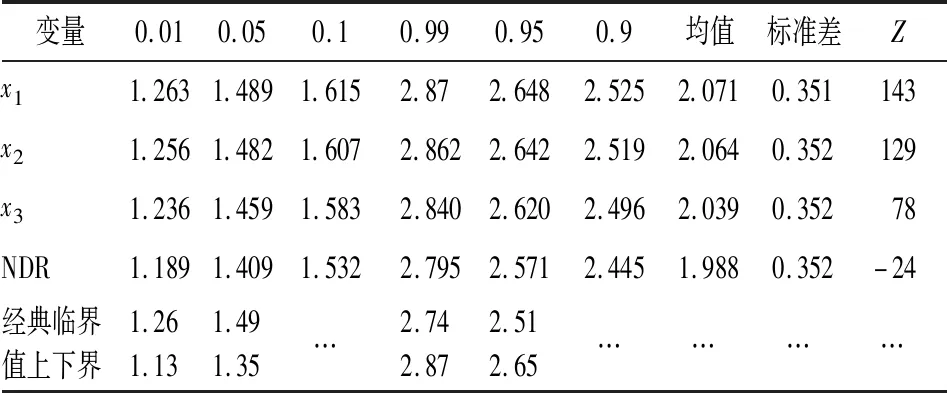
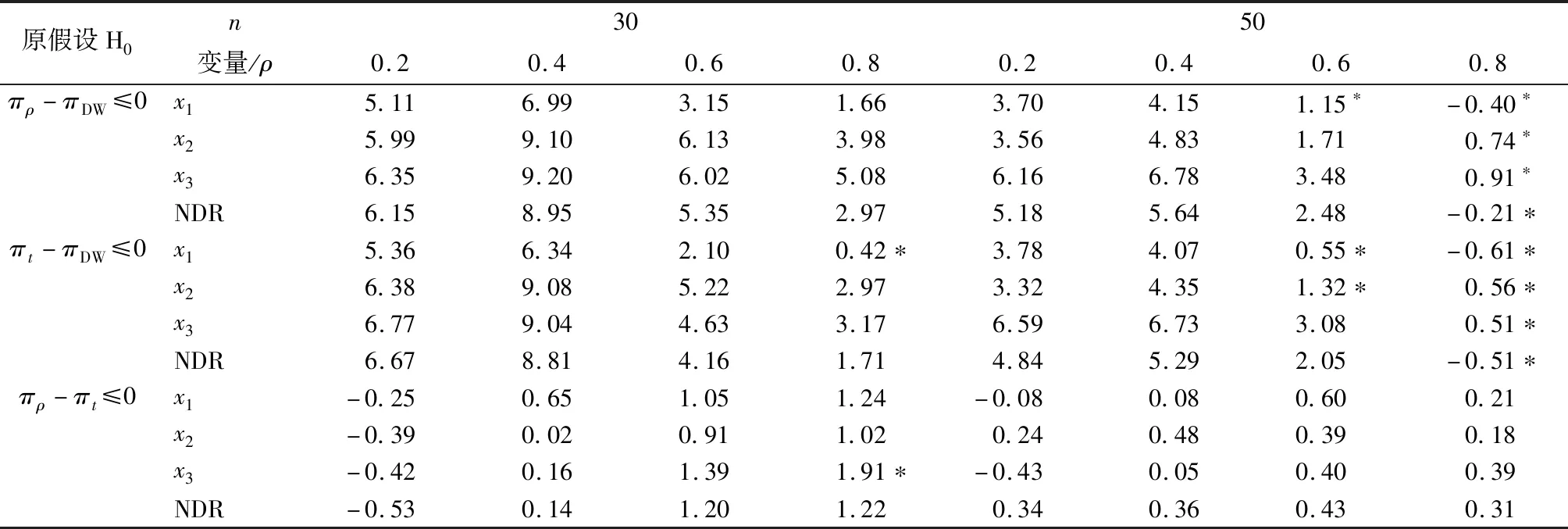
自相关性的检验方法有多种,如回归检验法、DW检验法、LM检验等。回归检验法是以残差et为被解释变量,以残差滞后项et-1、et-2等为解释变量建立辅助回归方程,如果方程显著成立,则模型存在自相关性。回归检验法的优点是一旦确定了模型存在自相关性,也就同时知道了自相关的形式,而且它适用于任何类型的自相关性的检验[1]。但是回归检验法由于没有明确的临界值,在实际中几乎没有得到应用。在实际应用中,一阶自相关性是人们最常考虑的形式, DW检验是检验一阶自相关性的一种经典方法,在一般的计量经济学教科书中,DW检验是重点介绍的自相关检验方法,许多统计分析软件在建立模型时也将DW统计量值作为基本统计量直接输出。由于DW统计量的分布及其临界值,不仅与样本容量n和解释变量数目k有关,还与解释变量序列的具体取值有关。Durbin和Watson考虑了不依赖于解释变量取值的两个极限分布,DW统计量位于这两个极限分布之间[2]。所以,Durbin和Watson根据样本容量n和解释变量数目k,在给定置信度α下,建立了DW检验统计量的下临界值dL和上临界值dU[3]。若DW≤dL,则有正自相关;若dU 此外,DW检验的使用需要满足一些先设条件,如:待检验的回归模型包含截距项,解释变量X是非随机的,解释变量中不包含滞后的被解释变量等。刘明和王永瑜对这些先设条件存在的原因逐一进行了分析讨论,并由此引出另一些不被注意的先设条件[5]。当模型中含有被解释变量的滞后项时,DW统计量的取值有经常偏向于2的缺陷,Durbin提出使用h统计量,对含有被解释变量滞后项模型的自相关性进行检验[6]。为了克服DW检验的缺陷,统计学家Breusch和Godfrey(1978)提出了一种新的检验方法,即拉格朗日乘数检验法(LM检验)。这种方法允许被解释变量的滞后项存在,同时还可以检验高阶自相关[1]158。若无自相关的原假设为真,在大样本情况下,LM统计量渐近服从2分布。 但在大多数应用中,样本往往都不是很大。在样本不大的情况下,LM统计量的分布与2分布会有较大差距,用2分布的临界值进行检验,可能会给出错误的结果。Mei-Yu Lee指出,由于受样本量和自变量个数的影响, LM统计量在小样本情况下并不趋向于卡方分布,只有当样本量大于1 000时, LM统计量才接近卡方分布[7]。另一方面,由于LM检验不能直接确定自相关的阶数。针对这一问题,刘汉中提出对残差最高阶滞后项的回归系数进行常规的t检验,以此来确定自相关的阶数[8]。但由于辅助回归中的残差滞后项具有随机性及相关性,残差最高阶滞后项回归系数的t统计量并不服从标准t分布,用常规的t检验可能会给出错误的检验结果。 本文主要做了以下几项工作:第一,针对不同的解释变量,运用蒙特卡罗模拟方法,通过EViews软件编程,得到DW检验、回归检验、LM检验的临界值和LM检验中最高阶滞后项回归系数t统计量的临界值,并分析临界值的一些特点。根据DW检验和LM检验的模拟临界值进行序列自相关检验,可以避免DW检验存在不确定区域和LM检验的临界值不准确的缺陷。第二,当用模拟方法确定临界值时,可采用回归检验法进行自相关性检验,即用残差et对et-1回归系数的估计量ρ和其t统计量作为检验统计量,分别称为ρ检验和t检验。通过蒙特卡罗模拟方法,计算了DW检验和回归检验法的检验功效,结果表明,回归检验法的检验功效优于DW检验,可以作为DW检验的替代方法。第三,在LM检验中,通常通过对最高阶滞后项系数进行t检验以确定自相关的阶数,但模拟计算表明,LM检验中最高阶滞后项系数的t统计量不服从标准t分布,且小样本情况下差距较大,不能用标准t分布临界值进行检验,在实际检验时,可以用模拟方法计算临界值。最后举了两个应用案例。 为节省篇幅,本文仅就DW检验时,蒙特卡罗模拟的具体方法及EViews程序进行说明,其他检验时的方法类似(1)读者若需要,可向作者索要EViews软件的程序,读者在对实际模型进行DW检验时,只要参照说明进行操作,就可以计算出相关检验的临界值。。假设在实际应用中,一个被解释变量y与k个解释变量x1,x2,…,xk之间有线性模型关系,当给定解释变量的样本序列时,由于DW检验的原假设与随机误差项之间相互独立,因此可取: y=b0+b1x1+b2x2+…+bkxk+μ, μ~i.i.dN(0,σ2) (1) 由于DW检验的临界值,与样本容量n、解释变量数目k和解释变量序列的具体取值有关,而与模型的系数及标准差σ无关。因此在实际应用中计算模拟临界值时,解释变量x1,x2,…,xk必需取实际的样本数据,系数b0,b1,…,bk和标准差σ可任意取值。但为了提高模拟结果的精度,可分别根据实际样本数据中的被解释变量y关于解释变量x1,x2,…,xk回归所得的系数估计值和误差项标准差估计值进行轻微调整得到。蒙特卡罗模拟方法的具体步骤如下:第一步,对系数b0,b1,…,bk和标准差σ赋值,输入x1,x2,…,xk的样本数据;第二步,产生随机序列μ;第三步,根据公式(1)计算序列y;第四步,将y关于解释变量x1,x2,…,xk回归,并计算DW统计量值;重复第二至第五步,本文重复50万次,得到50万个DW统计量值,再计算50万个DW统计量值的0.01、0.05、0.1、0.99、0.95、0.9分位数。其中0.01、0.05、0.1的分位数分别为正序列相关检验时,显著性水平为0.01、0.05、0.1的DW检验临界值;0.99、0.95、0.9分位数分别为负序列相关检验时,显著性水平为0.01、0.05、0.1的DW检验临界值。由于重复次数越多,模拟临界值与真实临界值越接近,本文进行了高达50万次的重复实验,所得模拟临界值将很接近真实的临界值。 为研究DW检验临界值的特点,本文选取了约20个实际的时间序列数据和几组标准正态分布、均匀分布的随机数序列,针对不同的样本量,进行了模拟计算。从这些模拟结果可以得出一些普遍性的结论。因篇幅所限,本文仅给出样本量n为30的一元线性回归模型时,解释变量分别取有代表性的四种变量时的模拟结果,见表1所示。表1中的变量x1、x2、x3是威廉·H.格林提供的数据文件TableF5-1中的变量M1、TBILRATE、INFL从1976年起的100个数据(2)数据文件可从参考文献[9]中附录F所示网址中下载。[9],NDR是一个固定的标准正态分布随机数序列(3)根据作者的理解,随机数序列具有更广泛的代表性。。这里取各变量的前30样本值。查DW检验临界值表可得,一个解释变量,样本量为30时,显著水平分别为0.01和0.05时临界值的上界和下界,也在表1中列出。表1中的最后三列分别给出各变量对应的50万个DW统计量的均值、标准差,以及对于检验H0:μ=2,H1:μ2的检验统计量Z值,Z值服从标准正态分布。Durbin和Watson在其经典论文中没有给出显著水平为0.1的临界值,作者所见的文献中也没有显著水平为0.1的临界值。为论述方便,下文将DW检验临界值表中的临界值称为经典临界值。 表1 样本数为30不同解释变量时DW检验的模拟临界值 根据表1及其他许多次随机模拟实验的结果可得如下结论:首先,DW统计量的分布不是关于2对称的分布,但都在经典临界值的上、下界区间内。从Z值可以看出,全部都非常显著地拒绝原假设。由此可知,对于变量x1、x2、x3,其DW统计量的均值大于2;而对于变量NDR,其DW统计量的均值小于2。其次,不论是正、负序列相关检验,对于实际的时间序列,各个模拟临界值都与经典临界值中较大的一个比较接近,而且在很多情况下,在保留两位小数时,模拟临界值与经典临界值中较大的一个完全相等;只有解释变量是随机数序列时,模拟临界值位于两个经典临界值的中点附近。也即当解释变量波动频数与波动幅度较小时,模拟临界值与经典临界值中大的一个相差较小,而当解释变量波动频数与波动幅度较大时,模拟临界值与经典临界值的上界相差较大。由于大多经济序列都存在趋势性,波动不大,所以在实际应用中,如果不通过模拟方法计算临界值,也可以直接采用经典临界值的上界进行检验。 本文仅就一阶自相关检验时,回归检验法的临界值及其特点进行研究。此时回归检验法就是将残差et关于其一阶滞后et-1作辅助回归,可以用回归系数的估计量ρ进行检验,也可以用其t统计量进行检验,为方便起见,以下分别称为ρ检验和t检验。通过蒙特卡罗模拟方法,可以得到ρ检验和t检验的临界值。由于将残差et对et-1回归时样本数少一个(对更高阶滞后项回归时以此类推),本文参照EViews软件中序列相关LM检验时将缺失的残差滞后值设为零的做法(下文在涉及此类的回归时都采用此做法),使辅助回归方程的样本量与原方程相同,以减小估计误差,增加模拟临界值的准确性,提高检验功效。 实际上,DW检验除了存在不确定区域外,还有一个问题是DW统计量比较复杂,不易为初学者所理解。在许多相关的文献中,在介绍DW检验时,都将DW统计量转化为残差et与et-1的相关系数ρ的表达式,再通过ρ分析DW统计量的取值范围及具体意义。根据作者的理解,Durbin和Watson提出DW检验,主要是为了能够在理论上研究DW统计量的分布特性,确定其临界值。但当我们用模拟方法确定临界值时,则用回归检验法更加直接。而且后文的模拟结果表明,回归检验法的检验功效高于DW检验。 由于ρ及其t统计量的取值可正可负,所以当进行负的自相关检验时,是左侧检验,对应于显著性水平为0.01、0.05、0.1的临界值分别是相应50万个模拟统计量值的0.01、0.05、0.1分位数;当进行正的自相关检验时,是右侧检验,对应于显著性水平为0.01、0.05、0.1的临界值分别是相应50万个模拟统计量值的0.99、0.95、0.9分位数。 与前文相同,这里仅给出样本量n为30的一元线性回归模型时,解释变量分别取表1中的四种变量时的模拟结果,见表2所示。表2中的最后三列分别给出各变量对应的50万个ρ值及其t统计量的均值、标准差,以及检验“H0:总体均值=0”的Z统计量值。Z统计量服从标准正态分布。另外需要说明的是,本文在模拟实验中,针对每一组解释变量和被解释变量的回归方程,同时计算DW统计量、ρ及其t统计量和它们的临界值,这样三种临界值之间的相对误差更小,后文根据此临界值所得的三种检验功效也更具可比性,结论更为可靠。 表2 样本数为30不同解释变量时回归检验法的模拟临界值 从Z值可以看出,全部均非常显著地拒绝原假设。由此可知,在各种情形下,ρ值及其t统计量的均值都小于0,它们的分布不是关于0对称的分布。从各临界值也可以看出其具有不对称性。在表2中也给出了相应样本量时的标准t分布临界值,由于回归检验法中的回归没有常数项,样本量为30时对应自由度为29的t分布。可以看出,回归检验法中的t统计量的临界值与标准t分布的临界值有较大差距,所以当用回归的t统计量进行检验时也不能使用标准t分布临界值,需要用模拟方法计算临界值。 评价检验方法好坏的主要依据是检验水平与检验功效。检验水平是犯弃真错误的概率,即误差序列不存在自相关,被判断为存在一阶自相关,检验水平越小越好。检验功效是原假设为假而被拒绝的概率,即存在一阶自相关时被判断为存在一阶自相关的概率,检验功效越大越好。当两种检验方法用各自的检验临界值进行检验时,检验水平即为显著性水平。所以,当取相同的显著性水平进行检验时,各种方法的检验水平没有区别,检验方法的好坏在于它们的检验功效。首先对满足DW检验条件的自相关模型,运用模拟方法计算DW检验、ρ检验和t检验的检验功效。本文以误差项存在自相关的一元线性回归模型为例。针对给定解释变量的样本序列,构造自相关模型: yt=b0+b1xt+μt, μt=ρμt-1+εt,εt~i.i.dN(0,σ2) (2) 在实际模拟实验时,系数b0、b1、ρ和标准差σ要取具体值,但除ρ以外,其他参数的值不影响检验功效,而不同的ρ值有不同的检验功效。εt为独立同分布的正态序列,这时只要每随机产生一个序列εt,就可以计算序列yt;将yt关于解释变量xt回归,提取DW统计量和残差序列et;再将et关于et-1作辅助回归,得到ρ的估计值及其t统计量值。重复上述步骤,本文重复50万次,得到50万个DW统计量值、ρ的估计值及其t统计量值。再将各统计量值与各自的临界值比较。当ρ取正值时,即假设误差项存在正的自相关,对于DW检验,如果计算的统计量值小于临界值,则检验结果为存在正自相关;对于ρ检验和t检验,如果计算的统计量值大于临界值,则检验结果为存在正自相关。再计算出50万次实验中存在自相关的频率,即为相应的检验功效。作者对各种不同的情形进行了大量的模拟计算。限于篇幅,本文给出以表1中的4个解释变量,样本数n分别为30和50,ρ值分别为0.2、0.4、0.6、0.8的情形,以显著水平α=0.05的模拟临界值模拟计算的检验功效,结果见表3所示。 表3及其他的模拟结果均显示,只在样本量为50、ρ值为0.8时,由于检验功效很接近1,三种检验方法的功效,在保留4位小数时,几乎完全相等,其他情况下,DW检验的检验功效均小于ρ检验和t检验。由于检验功效是被检验为自相关的次数与总次数的比率,根据两个总体比率之差的检验原理,检验H0:π2-π1≤0,H1:π2-π1>0的统计量: (3) 服从标准正态分布。π1和π2分别是两种检验方法的真实检验功效,p1和p2分别是两种检验方法的模拟功效,N是模拟的总次数,本文中N=50万。根据表3可以分别计算得到三种原假设H0:πρ-πDW≤0、H0:πt-πDW≤0 、H0:πρ-πt≤0下的检验统计量Z值,见表4所示。 表3 DW检验与ρ检验、t检验的检验功效比较(=0.05) 表3 DW检验与ρ检验、t检验的检验功效比较(=0.05) 变量n3050ρ/方法0.20.40.60.80.20.40.60.8x1DW检验0.24770.60840.87520.97170.37110.83420.98460.9992ρ检验0.25210.61520.87730.97220.37470.83730.98490.9992t检验0.25230.61460.87660.97180.37480.83720.98470.9992x2DW检验0.24570.60180.86830.96860.37100.83280.98430.9992ρ检验0.25080.61070.87240.97000.37440.83630.98480.9992t检验0.25120.61060.87180.96970.37420.83600.98470.9992x3DW检验0.24650.60560.87340.97050.36820.83050.98360.9990ρ检验0.25200.61460.87740.97220.37420.83560.98450.9991t检验0.25240.61440.87650.97160.37460.83560.98440.9990NDRDW检验0.24740.61890.89300.98070.37600.84580.98860.9996ρ检验0.25270.62760.89630.98150.38100.84990.98910.9996t检验0.25320.62740.89560.98120.38060.84960.98900.9996 表4 三种原假设下的检验统计量Z值 表4中原假设H0:πρ-πDW≤0、H0:πt-πDW≤0时,*号表示显著水平0.05下不拒绝H0。从表4可见,只在n=50且ρ=0.8时,全部不拒绝原假设;另外在n=50且ρ=0.6时,有三个Z值不拒绝原假设,在n=30且ρ=0.8时,有一个Z值不拒绝原假设。其余情况均拒绝原假设。这表明,除检验功效很接近1时,差别不显著外,ρ检验和t检验的功效显著大于DW检验。表4中原假设H0:πρ-πt≤0时,Z值大部分为正,表明大多数情况下,ρ检验的功效大于t检验,但几乎全部不显著,只有一个(含*号的)在显著水平0.05下拒绝H0,可以认为t检验和ρ检验的功效没有显著差别。因此,应该用ρ检验和t检验作为DW检验的替代方法。 为研究LM检验临界值的特点,作者选取了多个实际的时间序列数据,针对不同的样本量进行了模拟实验。大量的模拟计算表明,LM检验的实际临界值除了与序列相关的阶数p有关外,在样本量不很大时,还与样本量n、解释变量取值、解释变量的个数k有关。但LM检验的实际临界值与系数b0,b1,…,bk和标准差σ的具体取值无关。表5中给出序列相关阶数p=2和4,样本量为20、100、1 000,解释变量取1个、2个及3个时较有代表性的部分模拟结果。表5中同时给出相对应的50万个LM统计量的均值、标准差,及二阶对应的检验H0:μ=2,H1:μ>2和四阶对应的检验H0:μ=4,H1:μ>4(2(2)的均值为2,2(4)的均值为4)的检验统计量Z的值。 从表5可以得出如下结论:第一,样本量较小时,LM统计量的分布与相应的2分布有很大差异,因而LM检验的临界值与相应的2临界值有很大差距,当解释变量个数增加时,多数情况下差距会更大,当序列相关的阶数p增加时,差距也可能会更大,而且差距没有固定的方向性。由均值和方差可见,例如,当样本量n=20,p=4,解释变量为x3时,LM统计量的均值比2(4)的均值大0.328,LM统计量的方差比2(4)的方差小1.703;而当解释变量为x3、x6时,LM统计量的均值比2(4)的均值大1.027,LM统计量的方差比2(4)的方差小0.455。从临界值看,例如当样本量n=20,解释变量为x3,p=4时,显著水平为0.01的LM检验临界值比卡方临界值小1.94;显著水平为0.05的LM检验临界值比卡方临界值小0.431。第二,即使当样本量达到很大的1 000时,LM统计量的分布也很可能与相应的2分布有显著差异,两种临界值也可能有比较大的差距。由表5中Z值可知,当n=1 000时,在所模拟的各种情况下,都在显著水平0.01下拒绝原假设,即LM统计量的均值与相应的2分布的均值有显著差异,因而LM统计量的分布也很可能与相应的2分布有显著差异。从临界值看,例如当n=1 000时,在解释变量为x4,x5,x7,p=2时,显著水平为0.01的LM检验临界值比卡方临界值大0.135;显著水平为0.05的 LM检验临界值比卡方临界值大0.102,也可以认为是比较大的差距。 表5 各种情况下LM检验模拟临界值与2临界值的比较 表5 各种情况下LM检验模拟临界值与2临界值的比较 注:x4是从1993年1月8日起的上证综合指数的周收盘价,x5是1999年11月18日起的上证综合指数的日收盘价;x6是参考文献[10]提供的数据文件TableF5-1中的变量REALDPI,1976年第1季度至2000年第4季度的100个数据;x7是2011年7月6日至2017年9月5日上证指数日收盘价,共1 500个数据。其他变量同前。 由于LM检验不能直接确定自相关的阶数。在实际运用中,通常是从一阶开始逐次向更高阶检验,并对最高阶滞后系数进行t检验以确定自相关的阶数。但最高阶滞后系数的t统计量并不服从标准t分布,用常规的t检验可能会给出错误的检验结果。为研究LM检验中最高阶滞后回归系数t统计量的分布及其临界值的特点,作者选取了与前面相同的多个实际的时间序列数据,针对不同的样本量,当随机干扰项存在一阶、二阶自相关时分别按二阶、三阶序列相关进行LM检验时,最高阶滞后回归系数t统计量的分布及其临界值。大量的模拟结果表明,最高阶滞后回归系数t统计量的实际临界值在样本量不很大时,与样本量n、解释变量取值、解释变量的个数k有关,但与系数b0,b1,…,bk和标准差σ的具体取值无关。本文仅给出较有代表性的部分结果,见表6所示。表6中最后一列的Z值是检验“H0:总体均值=0”的统计量值。表6中也给出了相应自由度的标准t分布临界值。 表6 实际一阶自相关按二阶LM检验时滞后二阶回归系数t检验模拟临界值(单侧) 从表6及其他许多次随机模拟实验结果可以得出如下结论:第一,从Z值可以看出,全部均非常显著地拒绝原假设,说明在各种情形下,其t统计量的均值都显著小于0,它的分布不是关于0对称的分布。所以当用t统计量进行检验时,应该用单侧检验。第二,模拟标准差均小于t分布的标准差,所以导致左边的临界值与标准t分布临界值差距较小,右边的临界值差距较大。第三,随着样本量增大,模拟临界值与标准t分布临界值差距越来越小,解释变量个数越多,临界值的差距普遍越大。所以,当对LM检验中最高阶滞后回归系数进行t检验时不能使用标准t分布临界值,需要用模拟方法计算临界值。 为了更好地说明以上检验方法的应用,本文以两个案例分别说明一阶序列相关检验和高阶序列相关的LM检验的具体过程。 以Kt、Lt、Yt分别表示1978—2000年陕西省资本存量、就业人数和地区生产总值[10],建立C-D生产函数模型,得回归结果如下: lnYt=-2.805+0.862lnKt+0.429lnLt+et, R2=0.998,DW=1.244 3 (4) 查DW临界值表,可得显著水平为0.05时,dL=1.17,dU=1.54;显著水平为0.01时,dL=0.94,dU=1.29。两种显著性水平下均有dL 1.计算三种方法的模拟临界值。先建立样本量为23的工作文件,将lnKt、lnLt分别录入至以x1和x2命名的序列中,因为DW检验和回归检验法的模拟临界值与系数b0,b1,…,bk和标准差σ的具体取值无关,所以本文本着简洁的原则,对式(4)中的系数估计值稍作调整,取b0=-3,b1=0.86,b2=0.43,σ=0.3,运行模拟程序,可得DW检验、ρ检验和t检验的模拟临界值如表7所示,本例为正相关检验,所以只给出正相关检验的临界值。 表7 一阶序列相关性检验三种方法的正自相关模拟临界值 2.三种模拟方法的检验结果。由DW=1.244 3<1.279,可知在0.01的显著水平下,DW检验结果为模型存在正的一阶自相关。将式(4)中的et关于et-1回归,可得ρ和t统计量的值分别为0.372 8和1.841 9,分别大于ρ检验和t检验在0.01的显著水平下的临界值,即ρ检验和t检验结果为模型存在正的一阶自相关。也即三种检验的结果相同。 实际上,当检验结果为存在一阶自相关时,一般来说三种方法都会得出相同的结论。但本文的研究表明,ρ检验和t检验的检验功效大于DW检验的检验功效,这意味着当用ρ检验和t检验得出模型不存在一阶自相关时,检验正确的可能性较大。 以xt、yt分别表示我国1978—2004年国内生产总值和进口总额[11],建立一元线性回归模型,得回归结果如下: yt=0.234xt-1966+et,R2=0.92, DW=0.389 (5) 由DW的值可知,该模型存在一阶自相关。再对该模型进行二阶的LM检验,结果显示,LM统计量的值为22.26,远远大于2(2)的临界值,也必然大于LM检验的模拟临界值。残差二阶滞后项的t统计量值为-1.872,查表可知,显著水平为0.05时,标准t检验的临界值t0.05(23)=-1.714,因-1.872<-1.714,所以在0.05的显著水平下,认为模型存在二阶序列相关性。 若用本文的方法计算t统计量的模拟临界值进行检验,则得出不同的结论。先建立样本量为27的工作文件,将xt录入以x命名的序列中,取b0=-2 000,b1=0.25,s=500,ρ1=0.9,p=1,运行EViews程序,可得残差二阶滞后项的t统计量,显著水平为0.01、0.05、0.1的左侧模拟临界值分别为-2.886、-2.151、-1.781。因为-1.872>-2.151,所以在5%的显著水平下,不拒绝原假设,即模型不存在二阶自相关。 进行计量经济分析时一般都要检验模型是否存在自相关性,对于一阶自相关性的检验,DW检验是一种经典方法。由于DW检验有上、下两个临界值,使检验存在两个不确定区域。在实际应用中,可以通过运行EViews程序得到模拟临界值。根据该模拟临界值进行检验,可以避免DW检验存在不确定区域的缺陷。而且,当用模拟方法确定临界值时,可用回归检验法,即将回归残差et对et-1作辅助回归的系数估计量ρ及其t统计量作为检验统计量,分别称为ρ检验和t检验。根据模拟所得的临界值,对DW检验、ρ检验和t检验的检验功效进行模拟计算,结果表明,在本文所进行的各种情况的模拟实验中,除检验功效很接近1的情形外,ρ检验和t检验的功效均显著大于DW检验。因此,ρ检验和t检验都可以作为DW检验的替代方法。对于高阶序列相关性的检验,LM检验是一种常用方法。在大样本情况下,LM统计量近似服从卡方分布,但在大多数应用中,样本往往都不是很大。大量的模拟结果表明,当样本量不是很大时,LM统计量的分布与卡方分布差距较大,其临界值与卡方分布的临界值差距较大,且解释变量的取值对临界值的影响较大,因此,在对高阶序列相关进行LM检验时,不能使用标准卡方临界值,需要用模拟临界值。而且LM检验不能直接确定自相关的阶数,在实际运用中,通常是从一阶开始逐次向更高阶检验,并对最高阶滞后系数进行t检验以确定自相关的阶数。大量的模拟计算结果表明,LM检验中最高阶滞后项回归系数t统计量并不服从标准t分布,所以与标准t分布临界值不同,且小样本情况下差距更大,所以对最高阶滞后系数进行t检验时也不能使用标准t分布临界值,需要用模拟方法计算临界值,以提高检验的精确性。二、蒙特卡罗模拟的具体方法及EViews程序
三、DW检验的模拟临界值及其特点
四、回归检验法的临界值及其特点

五、DW检验与ρ检验、t检验的检验功效比较
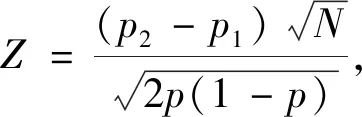

六、LM检验的模拟临界值及其特点

七、LM检验中最高阶滞后回归系数t检验临界值及其特点

八、实证案例
(一)一阶序列相关检验的实证案例

(二)高阶序列相关检验的实证案例
九、研究结论

