基于PID控制器的铝热连轧张力控制系统的设计与实现

(1.中南大学 机电工程学院，湖南 长沙 410083； 2.中南大学 高性能复杂制造国家重点实验室，湖南 长沙 410083； 3.中南大学 轻合金研究院，湖南 长沙 410083)

在铝热连轧生产中,张力是联系各个机架参数的桥梁和纽带，张力的重要性不言而喻。铝带轧制过程中，稳定的张力对于最终的板形有着至关重要的作用。机架间的张力两种控制方式,一种是液压压下调张,一种是速度调张,本文对速度调张进行建模与仿真[1-3]。传统张力控制系统一般采用PID控制器，PID控制器具有结构简单、易于控制的优点，但在张力控制系统中，PID控制器的参数一旦整定，在控制中是不变的，而实际工作中，由于张力控制系统参数是变化的，因此，常规的PID控制器难以满足张力控制系统的需要，且难以获得满意的控制效果[4-5]。

为了解决常规PID存在的问题，文献[6]～文献[8]采用粒子群算法对PID控制器进行优化，文献[9]～文献[11]采用神经网络对PID控制器进行优化，且都取得了不错的效果。但是对于特别复杂的问题，神经网络超调过大，找不到最佳控制参数，而粒子群算法则出现陷入局部最优的现象，因此，本文采用自适应权值粒子群算法对神经网络的权值和阈值进行寻优，再对PID控制器的参数进行整定，设计了一种自适应权值粒子群算法优化的神经网络PID控制器，该控制器保持了PID控制器简单、精度高的特点，又发挥了神经网络自学习、自适应和并行处理能力强的特点，同时引用自适应改进的粒子群算法，使得整个控制器更加快速、精确和稳定，从而得到控制器参数的最优解。

1 机架间张力方程

两机架间只存在一个张力，i机架的前张力等于i+1机架的后张力，机架间的张力由前机架板带出口速度与后机架板带入口速度差的积分得出：

(1)

式中，E为材料弹性模量；Li为第i机架到第i+1机架的间距。由于板带速度是时间、张力等变量的函数,故利用式(1)很难得到解析解，通常对式(1)采用数值解法。

在已知前张力初始值的情况下,可按照递推的形式迭代求出张力值[12],即

(2)

2 速度调张法

在稳态时，相邻两机架间铝带张力与前机架铝带的出口速度vh(i)和后机架铝带的入口速度vH(i+1)之差成正比；在动态时，理论分析证明，当速度vh(i)和vH(i+1)突变而产生速度偏差Δvi=vH(i+1)-vh(i)时，机架间的铝带张力呈指数规律变化。因此，可以用一个惯性环节来表示张力调节器，速度差Δvi和张力Ti之间的传递函数[13]可以表示为

(3)

式中，T(s)为张力变化的时间常数；λ为前滑系数；L为机架间的距离；vi为铝板带速度；KT为传递系数;A=Bh。由于L为常数，故时间常数T(s)与带钢速度vi成反比。

张力与速差之间为一阶惯性环节，张力传递函数模型如图1所示，其中，KT=1/λvi，τT=L/AEλvi,当vi不变时，KT、τT均为常数，但实际中vi是变化的，故KT、τT也在变化[3,14]。因此，张力模型参数是时变的，其两个主要参数都受到周围机架辊速的影响。

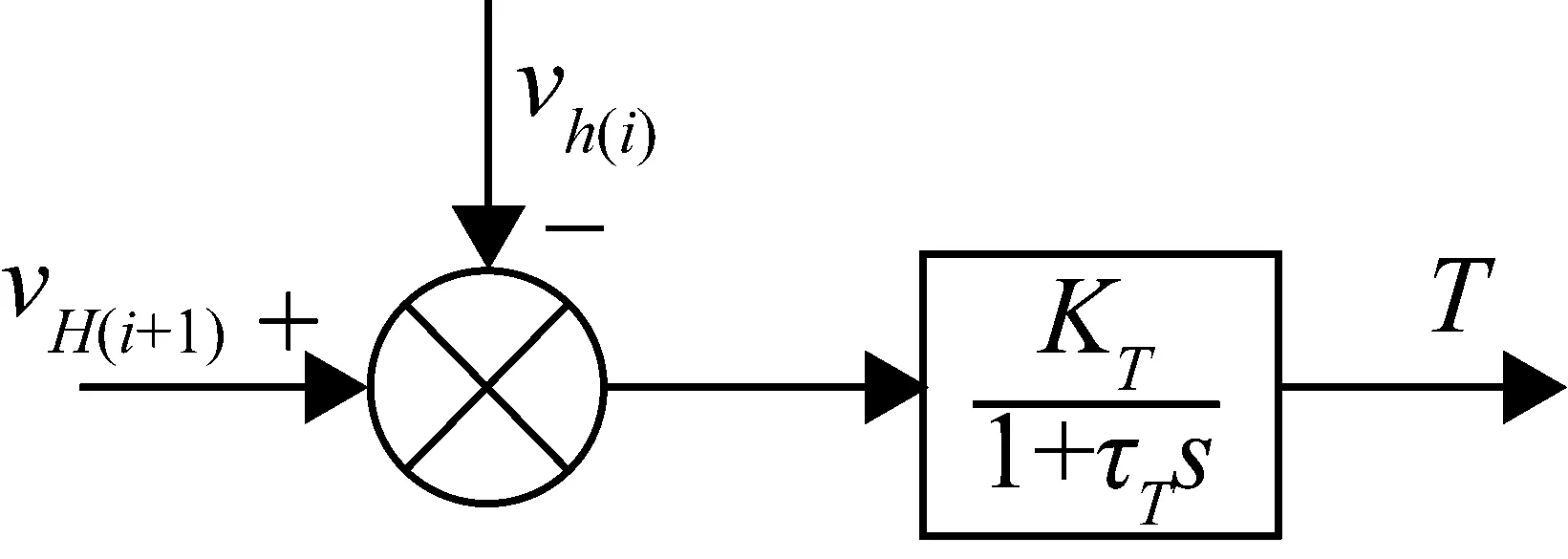
图1 张力传递函数模型

速度调张法的系统结构框图如图2所示，其中i为减速比，D为轧辊直径，速度闭环为转速电流双闭环系统，U为张力给定，T为产生的张力，vH(i+1)为下一机架入口速度，vh(i)为上一机架出口速度，热连轧张力系统是复杂的多环控制系统，应该先设计内环，再设计外环，从内到外分别为电流环、速度环、张力环[15]。

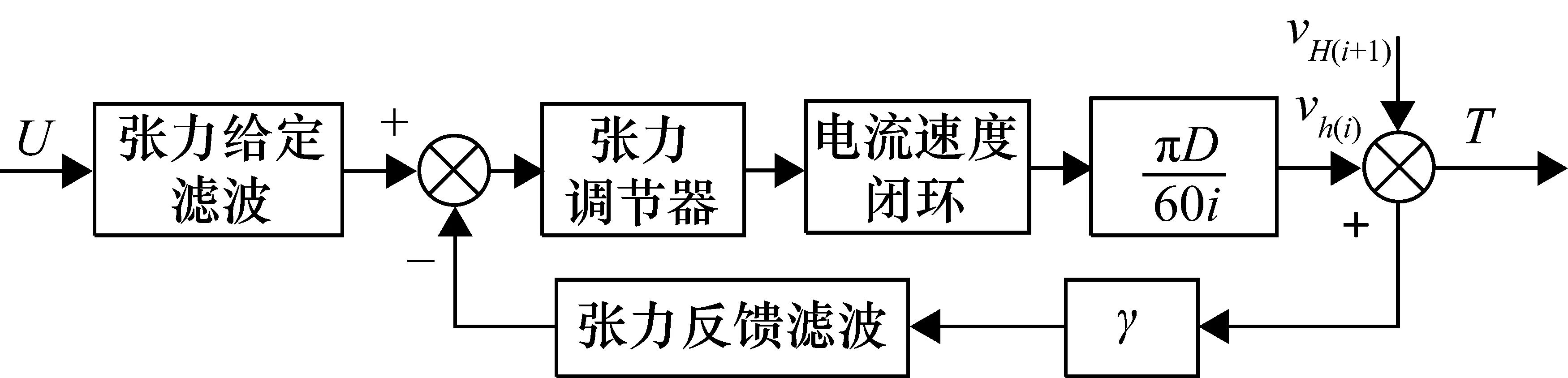
图2 速度调张法的系统结构框图

其中电流闭环为传递函数为

(4)

转速闭环传递函数为

(5)

张力闭环传递函数为

(6)

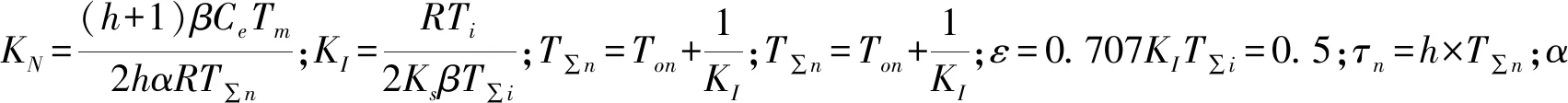
对各个参数合理取值可得张力闭环控制系统的模型为

(7)

3 神经网络PID控制器设计

PID控制器通常描述如下：

(8)

式中，KP为比例系数；KI为积分系数；KD为微分系数；Ti和Td分别为积分时间常数和微分时间常数。这些控制参数之间的关系为KI=KP/Ti，KD=KPTd。

PID控制器必须通过调整比例、微分和积分3种控制作用的线性组合才能取得良好的控制效果。神经网络PID是利用神经网络理论分别建立输入误差、误差变化率与PID控制器3个参数的二元函数关系，根据不同的映射关系，由误差和误差变化率在线调节PID的3个参数，神经网络PID控制器的结构如图3所示，可以看出它是一个闭环控制。

图3 神经网络PID 控制器的系统结构

3.1 神经网络的结构及其学习算法

PID神经元网络包括输入层、隐含层、输出层，隐含层由比例元、积分元、微分元组成，分别对应PID控制器中的比例控制、积分控制、微分控制。单控制量神经元网络的拓扑结构如图4所示，图4为一个3层前向神经元网络，网络结构为2-3-1，wij和wjk为网络权值。

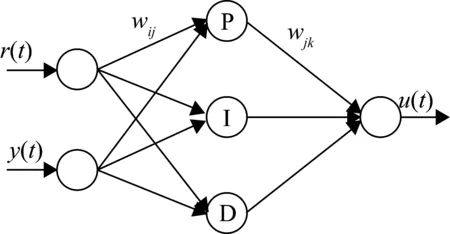
图4 神经元网络拓扑结构

(1) PID神经元控制规律的计算。

输入层有2个神经元，输出数据ri等于Ri，计算公式为

ri(k)=Ri(k)

(9)

隐含层有3个神经元，分别是比例神经元、积分神经元和微分神经元，神经元的输入计算公式为

(10)

(2) 隐含层神经元的计算。

① 比例神经元：

u1(k)=net1(k)

(11)

② 积分神经元：

u2(k)=net2(k)+u2(k-1)

(12)

③ 微分神经元：

u3(k)=net3(k)-net3(k-1)

(13)

(3) 输出层加权和的计算。

输出层为隐含层各个神经元输出值的加权和，计算公式为

(14)

式中，ri(k)为输入层神经元输出值；wij和wjk分别为输入层至隐含层、隐含层至输出层的权值。

3.2 神经网络权值修正

神经网络PID按照梯度修正法来修正神经网络的权值，其过程如下。

误差计算公式：

(15)

输入层到隐含层权值的修正公式：

(16)

输入层到输出层的权值修正公式：

(17)

式中，η为学习速率。

4 自适应权值粒子群算法

粒子群算法是一种随机优化算法，该算法必须首先初始化一组随机值作为粒子群，然后粒子再以一定的速度更新当前最优粒子和最优种群。每次更新最优个体pi、最优种群pg和粒子的速度V和位置Xi，最后得到一组最为合理的结果。粒子群算法简单、易于实现，但是容易出现早熟等现象，以致于不能全局寻优，因此，本文采用自适应权值粒子群算法对张力控制系统进行改进。

自适应权值粒子群算法[18]是一种启发式搜索算法，能够自适应地更新权值，并且能够保证粒子具有良好的全局搜索能力和较快的收敛速度。

自适应权值粒子群算法过程为：在一个S维的目标搜索空间中，有m个粒子，第i个粒子用一个S维的向量xi=(xi1,xi2,…,xiS)来表示，i=1,2,…，m，粒子的位置就是潜在的解。将xi代入目标函数就可以算出其适应值，目标函数解的优劣以适应值来衡量。第i个粒子的速度是S维向量，记为V=(Vi1,Vi2,…，ViS)。第i个粒子的最优位置为PiS=(P1S,P2S,…，PiS)，整个粒子群的最优位置为PgS=(P1S,P2S,…，PgS)。

如果f(x)为最小目标函数，那么粒子i的最优位置为

(18)

Kennedy和Eberhart用下列公式对粒子进行操作：

vis(t+1)=vis(t)+c1r1s(t)(pis(t)-xis(t))+

c2r2s(t)(pgs(t)-xis(t))

(19)

xis(t+1)=xis(t)+vis(t+1)

(20)

式中，i=[1,m]，s=[1,S]；c1和c2为非负的学习因子；r1和r2为相对的随机数，服从[0,1]均匀分布；vis∈[-vmax,vmax]，vmax为常数，视情况而定。

由式(19)和式(20)可知，c1和c2分别控制粒子向自身最优位置和全局最优位置移动的步长。vis∈[-vmax,vmax]，vmax为最大速度，如果搜索空间在[-xmax,xmax]中，则可以设定vmax=kxmax，0.1≤k≤1.0。Y.Shi和Eberhart对式(19)进行了改进：

vis(t+1)=w·vis(t)+c1r1s(t)(pis(t)-xis(t))+

c2r2s(t)(pgs(t)-xis(t))

(21)

式中，w为动力常量，非负。w较大时，前一速度对当前速度的影响较大，全局搜索能力较强；w较小时，前一速度对当前速度的影响较小，局部搜索能力较强。通过调整动力常量w值能够跳出局部极小值。

为了平衡算法的搜索能力，w引入非线性的动态权重，其表达式为

(22)

式中，wmax和wmin为w的最大值和最小值；f、favg和fmin分别为目标函数值、平均目标值和最小目标值。w因惯性权重随目标函数值自动改变，因此称为自适应权重。

当目标值集中时，惯性权重增大，而当目标函数分散时，相应的惯性权重将减少，当粒子的目标函数值优于平均目标值时，对应的惯性权重因子较小，从而保留该粒子。相应地，当粒子的目标函数值差于平均目标值，其对应的惯性权重因子较大，使粒子向较好的搜索区域靠拢。

自适应粒子群算法对神经网络的权值和阈值按照上述规律进行寻优，最后找到最优的PID参数。

5 仿真

由上文可知铝合金热连轧张力控制系统的传递函数为

(23)

自适应粒子群算法的参数设置为：c1=2，c2=2，种群总数为100，wmax=0.9，wmin=0.4，迭代次数为100，最小适应度值为0.1，最大速率为1。用单位信号对张力控制系统分别进行常规PID、自适应粒子群优化的PID、神经网络PID和PSO优化的神经网络PID进行仿真，其结果如图5所示。

图5为铝热连轧张力控制系统在几种PID控制器下的输出结果，由图可见，相比常规PID，自适应权值粒子群PID和神经网络PID都能够较快地达到稳定状态，并且超调量较小，自适应权值优化的神经网络PID的性能优势更加明显，其超调量和稳定时间均较小。由此可见，经过改进的神经网络PID优化效果十分明显，响应速度快，调节时间缩短，几乎没有超调，因此控制精度更高，而常规PID调节时间长，超调大，并且对非线性和复杂的张力控制系统难以满足其控制要求，容易产生不良板形，造成资源浪费。

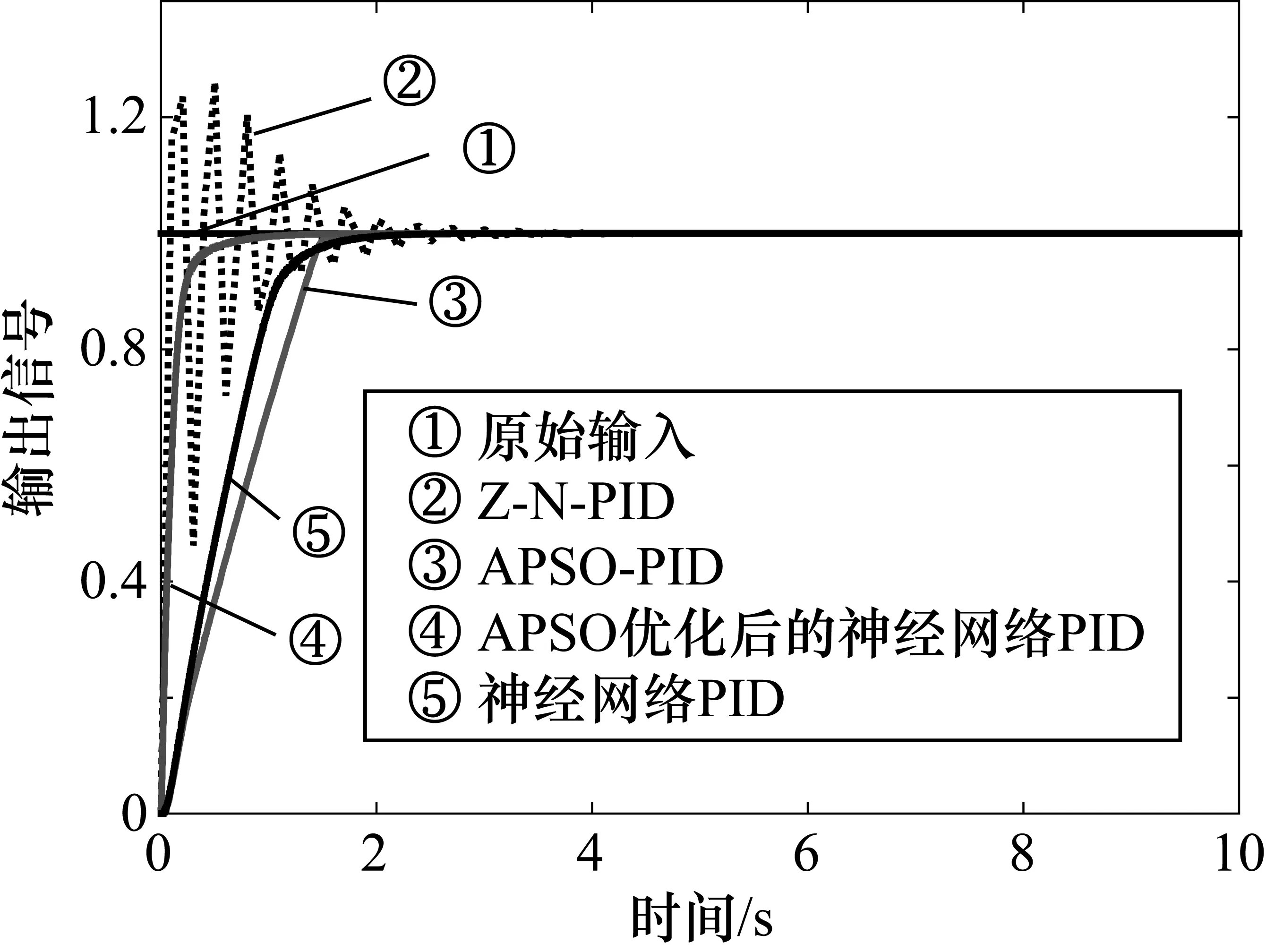
图5 仿真结果

6 结束语

针对神经网络PID控制器在铝热连轧过程中收敛速度慢的问题，提出一种粒子群优化算法，该算法引入自适应权重，能够通过目标函数值的改变而自动改变，从而调节全局搜索能力和收敛速度，能够保证算法有较好的全局搜索能力和较快的收敛速度，从而提高计算效率。通过仿真对比，在铝热连轧张力控制系统中自适应权值粒子群算法优化的神经网络PID控制器比其他PID控制器性能更佳，能够很好地改善板形。