基于递推最小二乘和改进支持度的WSN数据融合算法

(东南大学 仪器科学与工程学院，江苏 南京 210096)

在无线传感器网络中，通常布置有大量的传感器节点。一方面，由于监测环境复杂多变，这些传感器节点会不可避免地受到各种干扰，随机噪声对监测数据的影响不容忽略；另一方面，监控系统对节点能耗有较高要求，大量冗余数据的传输和处理将快速耗尽节点能量，使节点失效。因此，将数据融合技术应用在WSN中，可以增强数据的准确性(降低随机噪声的影响)，提高系统的可靠性(当某个或某些节点因能量耗尽或受到干扰而失效时，不会影响系统的正常感知)。

数据融合是指通过建模对不同源的数据进行处理[1]。通过对这些不同源数据的充分利用和合理支配，并结合数据估计、建模、采集管理等手段，依据某种准则综合考虑其在时间和空间上的冗余或互补信息，产生被测对象更准确的信息、更一致的解释和描述，以获得最大可信度的最优结果[2-3]。常用的算法有卡尔曼滤波算法和基于支持度函数的加权平均算法。

(1) 卡尔曼滤波算法。

卡尔曼滤波公式如下：

X(k|k-1)=A·X(k-1|k-1)+W(k-1)

(1)

Z(k)=H·X(k|k-1)+V(k)

(2)

P(k|k-1)=A·P(k-1|k-1)·AT+q

(3)

(4)

X(k|k)=X(k|k-1)+Kg(k)·V(k)

(5)

P(k|k)=(I-Kg(k)·H)·P(k|k-1)

(6)

式中，X(k-1|k-1)为系统上一状态的最优估计值；X(k|k)为系统现阶段的最优估计值；Z(k)为系统在现阶段的测量值；W(k-1)和V(k)是零均值、方差分别为q、r的相互独立的白噪声；Kg(k)定义为其增益阵；P(k|k)定义为其协方差阵。

(2) 基于支持度函数的加权平均算法。

支持度函数sup(a,b)表示两个值a,b间的相互支持程度，其必须满足以下条件：

①sup(a,b)∈[0,1];

②sup(a,b)=sup(b,a);

③ 若|a-b|<|x-y|，则sup(a,b)>sup(x,y)，a,b,x,y>0。

文献[4]提出一种新型支持度函数进行数据融合：

(7)

式中,α∈[0,1]为支持度函数的幅度；β>0为支持度衰减因子，β越大，支持度衰减越快。两个值越接近，它们的相互支持度越高。

通过该算法求得子系统内各节点的权值，以做加权融合运算。

1 数据融合系统模型

本文所提出的数据融合流程如图1所示，主要包括以下步骤：

① 通过自适应阈值函数，对各节点在一段时间内的原始数据进行异常数据剔除；

② 对各节点数据分别采用递推最小二乘法融合，求得其在该时间段内的估计值；

③ 将系统分解成多个子系统，分批对每个子系统的待融合数据采用基于改进支持度函数的加权融合算法，从而求得此刻该子系统的环境估计值，并将此值作为下一级融合的输入，以此类推进行融合。

2 节点内部数据融合

在WSN中，由于环境参数(如空气温湿度、土壤温湿度、光照等)变化缓慢，且有较大冗余，节点在相邻几个采集周期内的数据不会出现跳变现象，因此可以通过对各节点在一段时间内采集到的原始数据进行预处理来减少节点的数据传输量，最终达到减小能耗、延长生命周期的效果。

图1 数据融合流程

2.1 基于自适应阈值函数的异常剔除

由于环境噪声的存在以及传感器性能不稳定等因素，传感器会产生异常数据。为确保数据的可靠性，本文利用自适应阈值剔除这些异常值。

将一段时间内节点i采集到的原始数据自小到大排列为Xi=[x1,x2,…,xn]。

定义中位数为

(8)

上四分位数Fu定义为xm与xn间的中位数，下四分位数Fd定义为x1与xm间的中位数。

定义阈值函数：

ρ=β×(Fu-Fd)

(9)

式中，β与传感器节点精度相关。当测量值xj(j=1,2,…,n)满足

|xj-xm|>ρ

(10)

时，可视其为无效数据，将其剔除。

2.2 基于递推最小二乘法的数据融合

根据式(1)～式(6)，卡尔曼滤波算法的难点在于：

① 矩阵乘法甚至矩阵连乘运算的存在，导致运算复杂度增加；

② 当矩阵的阶数增加时，其求逆运算的复杂度以几何级数增加；

③ 由于卡尔曼滤波算法的核心在于迭代，即式(1)～式(6)均要进行多次的重新运算，计算量繁重。

在WSN中，各节点体积小，只能携带能量有限的电池，同时其低廉的价格必然造成存储器和处理器性能不佳的问题，将卡尔曼滤波直接应用在WSN中，可能出现计算量超出系统承载能力的情况。因此，降低卡尔曼滤波的计算量成为将其应用在WSN中的关键。

将卡尔曼滤波的矩阵参数做降维处理，即考虑一维系统，可将其简化为一维递推最小二乘法。递推最小二乘法计算过程较为简单，精度可以保证，同时无需掌握太多的系统先验知识，依靠测量值即可进行滤波。根据文献[5]和文献[6]，得到其递推关系如下：

(11)

xk=xk-1+pk(zk-xk-1)

(12)

式中，xk和xk-1分别为系统现阶段与前一阶段的估计值;zk为系统的当前测量值;x0与p0为系统初始值。为了提高在初期的融合精度，将前一个融合周期的融合值作为后一个融合周期的系统初值。

3 节点间数据融合

节点内部的数据融合会导致数据的大量丢失，为减小因传输过程中数据丢包等情况造成的影响，通常采用冗余传感器部署，通过节点间的数据融合获得最优估计值。

3.1 分批融合

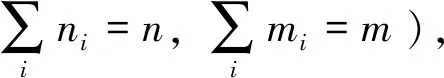
Nahin和Pokoski在文献[7]中定量证明了利用增加传感器的方法所获得的正确分类的边界线。通过使用N个相同的传感器来观测需要正确识别或分类的现象。假设每个传感器是统计独立的，且先验概率相等，通过计算机仿真表明增加参与融合的传感器数量能够提高观测数据的精度，但当传感器数目N超过某临界值(高精度传感器数目大于7或低精度传感器数目大于11)时，再继续增加传感器对观测精度的提高不会有明显有效的改善。

因此，将待融合的数据每7个为一个子系统，对每个子系统分别进行基于改进支持度函数的数据融合处理，并将融合结果作为下一级融合的输入值，以此类推进行分级融合。其流程图如图2所示。

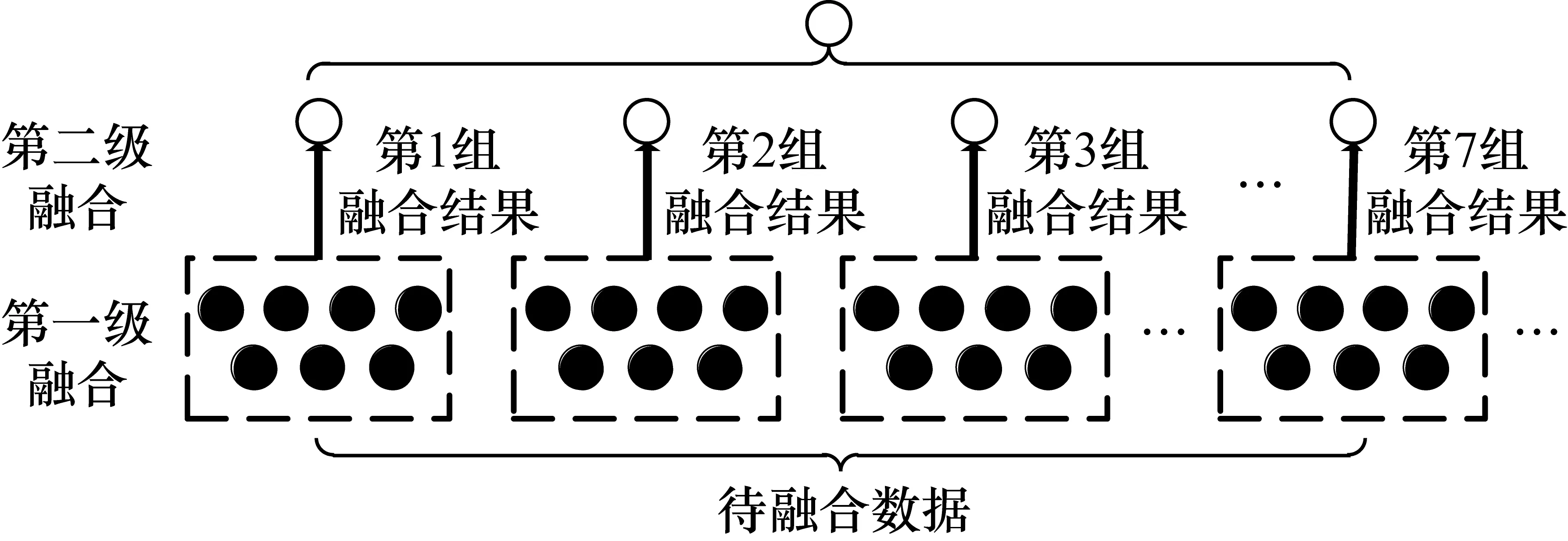
图2 分批融合示意图

3.2 基于改进支持度函数的加权融合算法

由式(7)可知，新型支持度函数存在以下问题：

① 使用该函数时，参数β是人为设定的，具有较强主观性，会影响实际融合的结果；

② 未考虑同一节点在观测区间内采集到数据的可信度，数据融合的精确度有待提高。

为了更可靠地评估节点数据间的支持度，提出一种改进的支持度函数。

根据灰色接近度理论[8]，定义节点i的自支持度si(k)为

(13)

式中，σi(k)为该节点的系统方差，其表达式为

(14)

式中，xi(k)为节点内部融合值;xik(t)为节点i在第k个采样周期内经过异常剔除后的采样值。

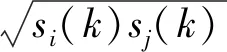
改进的支持度函数为

(15)

节点间的相互支持度矩阵为

(16)

节点i获得其他(n-1)个节点的总支持度为

(17)

对总支持度进行归一化处理，得到节点i的最优融合权值为

(18)

由此可得融合后该组传感器在此采样周期内的最优估计值为

(19)

4 实验与分析

设计了一套无线传感器网络，并于2016年8月在广州白云现代农业示范基地内的一座温室大棚进行了测试实验。该系统包括7个无线传感器节点。

4.1 数据传输量对比试验

在实验中，节点每隔30 s采集一次数据。然后以5 min为周期，将各节点连续的10个值作为节点内融合的输入，输出作为各节点在该周期内的估计值发送，以进行节点间的数据融合。与融合前需要发送的数据量相比，融合后的数据传输次数减少了90%，这可以有效减少节点无线通信的能耗，因此可以有效地延长网络的生命周期。

4.2 异常数据剔除效果分析

传感器节点在某5 min内采集的温度值如下：

a1=[36.4,34.0,34.3,34.6,34.8,34.7,37.4,35.4,36.0,36.5];

a2=[36.0,32.3,35.0,34.2,34.5,35.5,35.3,35.6,35.6,35.9];

a3=[36.2,34.9,32.5,35.0,34.1,33.8,37.5,34.9,35.4,36.2];

a4=[36.8,31.4,34.6,34.3,35.8,34.8,34.1,35.0,35.8,37.0];

a5=[35.9,32.0,33.9,34.5,36.0,35.0,34.0,35.3,35.0,36.4];

a6=[34.5,36.2,36.6,35.1,34.7,40.9,33.3,34.2,35.8,34.9];

a7=[34.9,36.9,37.9,35.4,35.1,40.5,34.8,34.6,35.3,36.5];

经过异常剔除后，得

b1=[36.4,34.0,34.3,34.6,34.8,34.7,35.4,36.0,36.5];

b2=[36.0,35.0,34.5,35.5,35.3,35.6,35.6,35.9];

b3=[36.2,34.9,35.0,34.1,33.8,34.9,35.4,36.2];

b4=[34.6,34.3,35.8,34.8,34.1,35.0,35.8];

b5=[35.9,33.9,34.5,36.0,35.0,34.0,35.3,35.0,36.4];

b6=[34.5,36.2,36.6,35.1,34.7,34.2,35.8,34.9];

b7=[34.9,36.9,35.4,35.1,34.8,34.6,35.3,36.5];

实验显示，温度差值均未超过2.5 ℃，因此本文采用的自适应阈值法能够准确有效地检验出数据的异常，保证后续融合数据的可靠性。

4.3 递推最小二乘法滤波检验

利用计算机随机生成一系列(35±2.5)℃的随机数据。数据共有100组，每组包含10个数值。分别利用递推最小二乘法和算术平均法对每组数据进行融合。采用递推最小二乘法和算术平均法融合后的均方误差分别为0.1956和0.1958。与一阶卡尔曼滤波相比，递推最小二乘法的计算量减少46.15%。可见，递推最小二乘法在减少运算复杂度的同时，仍然能够保证融合结果的较高准确性。

4.4 改进支持度函数检验

新型支持度函数的特征曲线如图3所示。根据本次实验各节点内部融合值及其系统方差可知，改进支持度函数的特征曲线位于D(a,b,1,0.5)与D(a,b,1,1)之间。实验中温度传感器的测量误差在 0.5 ℃左右。由图3可知，函数值在误差为0～0.5 ℃范围内时，衰减速度较缓；在误差为0.5～2 ℃范围内迅速衰减。这符合温度传感器的测量误差以及各点温度差值变化，因此能够在加权融合算法中显著地增加有效数据的权重，同时尽可能地减小误差偏大的数据对融合结果的影响。

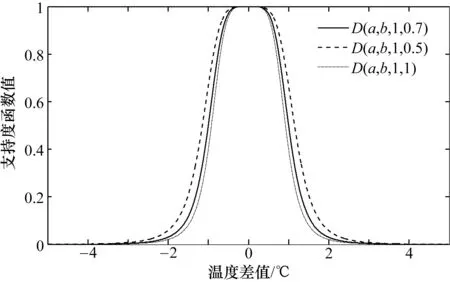
图3 新型支持度函数特征曲线图

4.5 实验结果

上述7组数据的融合结果如表1所示。

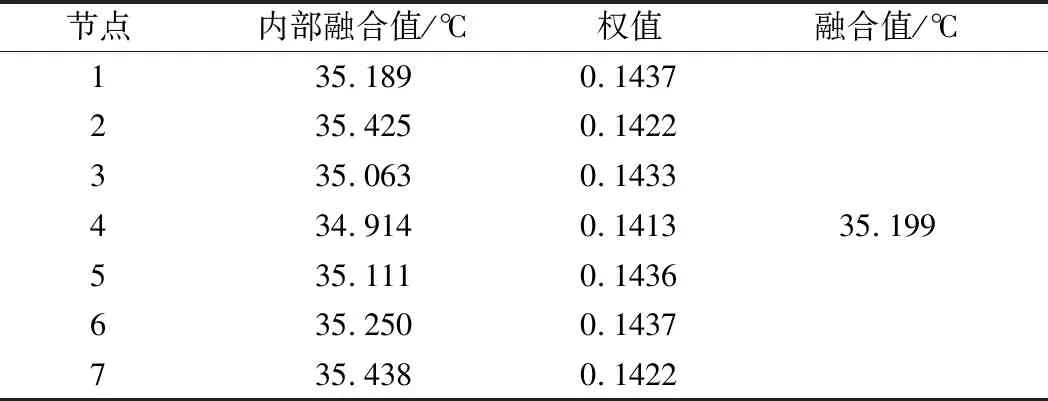
表1 部分数据融合结果

在该周期内，各节点的系统方差分别为：0.7588,0.2094,0.6598,0.3898,0.6899,0.6425,0.5998。经过融合后的系统方差为0.1520。可见，所提出的算法可以获得高精度的估计值。

在实验中，将高精度温度计读数作为真值，与改进后的融合值对比，其对比图如图4所示，融合后的均方误差为0.1597。可知，所提出的基于改进卡尔曼滤波和支持度的WSN数据融合算法能够有效地反映温度参数变化情况，且在实际应用中融合结果准确可靠。

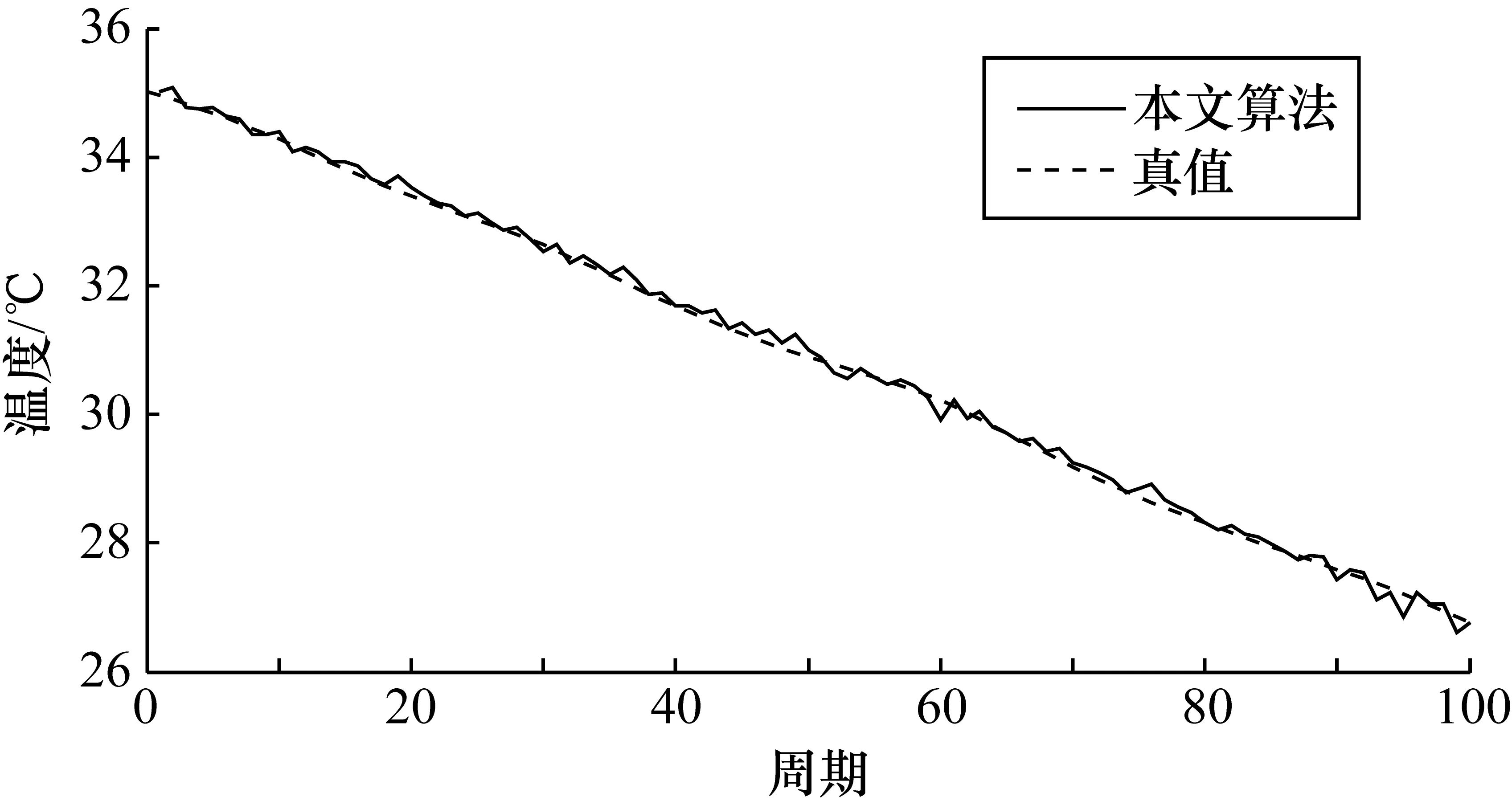
图4 本文算法融合值与真值对比图

5 结束语

本文提出了一种基于递推最小二乘法和改进支持度的WSN数据融合算法，并对其进行了实验验证。结果表明：自适应阈值函数能够有效剔除异常数据；基于递推最小二乘法以及改进支持度函数的数据融合算法可以有效减少数据传输和计算量，且融合后的数据精度能够满足实际应用要求。