高速铁路列车追踪间隔时间优化研究

(1.兰州交通大学 轨道交通电气化工程实验室，甘肃 兰州 730070;2.兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

影响列车追踪间隔时间的因素主要有信号设备、线路条件、运营管理技术和行车组织方式。国内外很多学者针对不同的影响因素对列车追踪间隔时间进行了优化调整[1]。

王宏刚、张琦等人采用遗传算法建立了高速铁路行车调整模型对高速铁路的行车方式进行了模拟[2]；杨欣、邵林等人采用TDE0(六段式参数配置优化模型)对高速铁路追踪间隔时间的动车组制动能力进行了仿真计算[3]；2014年日本学者Takagi为了使列车的追踪距离最小采用了同步控制策略对列车追踪间隔时间进行了优化[4]。

上述研究方案都是从信号设备和运营管理技术的角度出发对追踪间隔时间进行优化调整，只研究在平直道上追踪间隔时间的计算分析，忽略了线路条件(坡道附加阻力、曲线附加阻力和隧道附加阻力)对列车追踪运行产生的影响。

本文选用CRH380A型动车组及其运行参数，建立列车混合优化模型，研究在 CTCS-3级运行条件下，通过对制动距离进行多阶段划分，基于动态规划建立动车组追踪间隔时间的多阶段模型，采用COADP(自适应动态规划协同优化算法)对线路坡度化简方案进行优化求解，得到追踪间隔时间内各阶段变量的最优解、最优决策序列以及最优指标函数[5-6]。最后以成渝高铁线路数据为基础，通过动车组牵引计算仿真系统在所取的典型区间内对追踪间隔时间进行仿真，得出最优坡度下动车组运行的制动距离曲线和追踪间隔时间优化曲线。

1 列车混合优化模型

在不同的工况下，动车组牵引的计算方法不同，如果牵引计算强调列车的单质点特性，对车辆之间的车钩力可以忽略，那么建立列车的单质点模型对于简化计算过程具有很大的意义，通常在列车运行图或者列车时刻表的调整中，单质点模型的运用是比较适合计算条件的；单质点模型虽具有计算简单的优点，但不符合本文对计算精度的要求。在考虑列车长度的牵引计算模型中，列车的多质点模型通常是最常见的建模方案，在列车多质点模型中，考虑每一节车辆的受力分析，对列车运行中的每一节车辆的车钩力都进行计算，计算的精度得到了保证，但是计算量又很大。

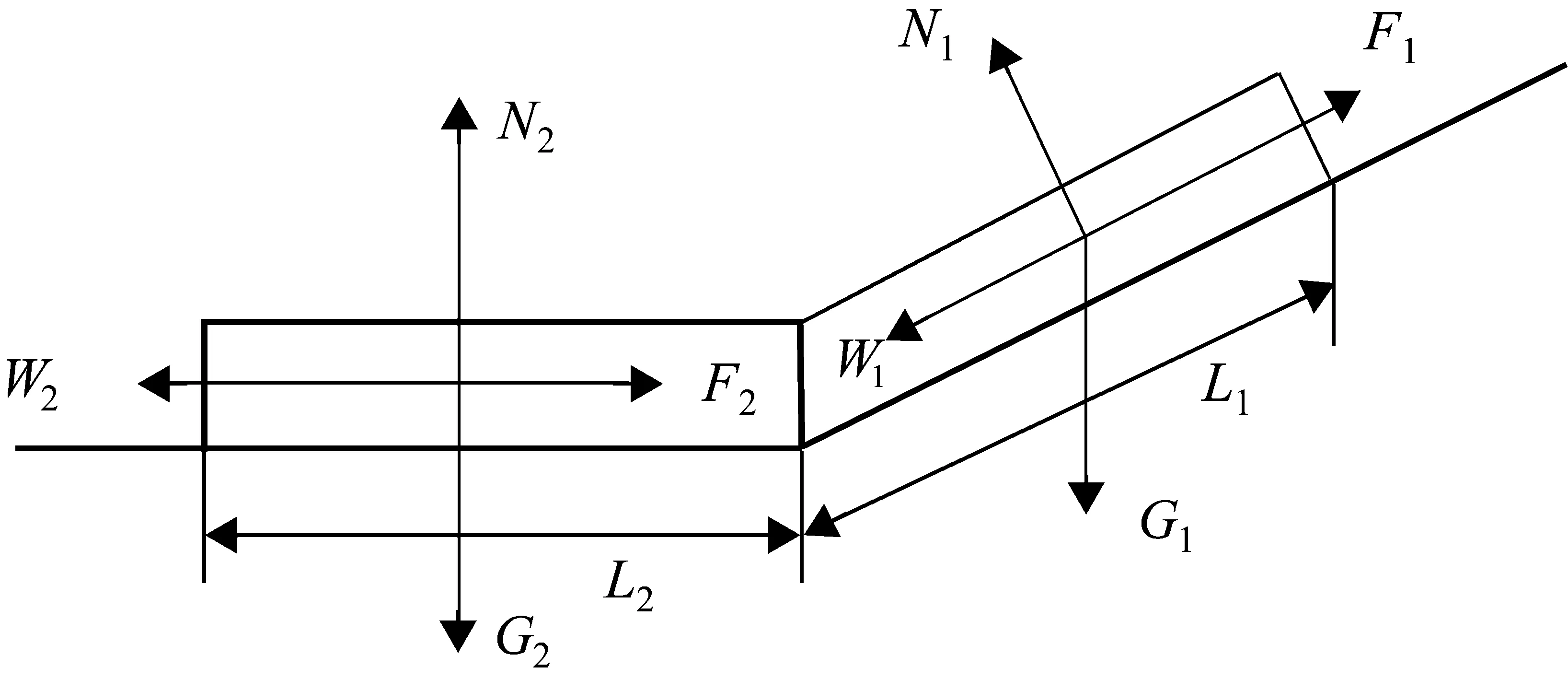
图1 列车混合优化模型受力示意图

本文在动车组牵引计算中，综合考虑铁路线路坡度节点和列车长度的关系，建立了列车混合优化模型，避免了高速列车实际运行中多质点模型计算量大的缺点，同时又对动车组牵引计算的精确度没有较大的影响[7]。所建立的动车组牵引计算模型的基本思路是：将动车组按变坡点划分为相互连接的若干段，每一段中所有车辆都处在同一坡度，所以把同一坡度中的这些车辆看作一个整体，在质量上按比例将整列车的质量分摊在每个处于同一坡段的车辆上，这样在同一坡段中就不需要计算车辆之间的车钩力，只在变坡点处计算车钩力。这样建立起来的列车混合优化模型不仅简化了动车组的牵引计算过程，合理地简化了相同坡段上列车车钩力的计算，而且突出了在坡度节点处的动车组各车辆间的纵向(车钩力)计算。

列车混合优化模型最突出的特点是大大减低了坡道附加阻力的计算过程，通过列车混合优化模型的基本原理可以得出式(1)所示列车处在两个不同坡段时坡道附加阻力的计算表达式：

(1)

式中，Wi1和Wi1分别为列车处于不同坡度部分的坡道附加阻力；L为列车长度。在坡道附加阻力的计算中，只需要计算不同坡段中各段车辆的坡道附加阻力，然后按照列车处于不同坡段的长度比例计算整个列车的坡道附加阻力[7-9]。在参考文献[7]～文献[9]后分析得出，如果按照本文中所取的列车编组进行计算，以8节车辆编组计算，则列车总长度为200 m左右，而以成渝高铁的线路数据为例，最小坡长为379 m，这样整列车最多会同时占用两个坡段，如果车辆编组为16节，那么同时占用的不同坡段也不会超过3个，即使出现超过3个的情况也可以按照混合优化模型进行分段计算。

2 不同坡度化简方案下的分段计算过程

2.1 不同坡度化简方案的多阶段模型

列车制动距离是在坡度化简后，通过牵引计算得到的各分段距离的累加和。以图2所示的一个制动距离内的纵断面分段示意图为例，以ΔS=400 m为等间隔距离划分列车制动距离，并建立制动距离的多阶段决策模型。

将总长3600 m的实例区段以400 m (可适当调整)为间隔划分为9个子阶段，在每一分段上有不同的坡度、曲线以及隧道附加阻力，都会对坡度化简产生不同的影响，由此计算得出的制动距离也不尽相同，在每个制动距离上依次划分，通过动态规划算法求解制动距离的最优值函数[10]。

图2所示的一个求制动距离最小值的9阶段决策问题，图中共含4段曲线，并给出了各曲线路段的参数，如第1段曲线的曲线半径、曲线长度和曲率分别为453 m、1000 m和26°；同时包含有4个坡段，如第1个坡段的坡度千分数和坡长分别为5.2和800 m。选取每一阶段的初始运行速度作为每一个阶段的状态变量xk，每一阶段的运行距离作为每一个阶段的阶段变量，则可以得出图3所示的动态规划多阶段模型图。通过COADP算法求解得到每一个阶段的最优值函数uk，最后得到整体的最优值指标函数J。

图2 纵断面分段示意图

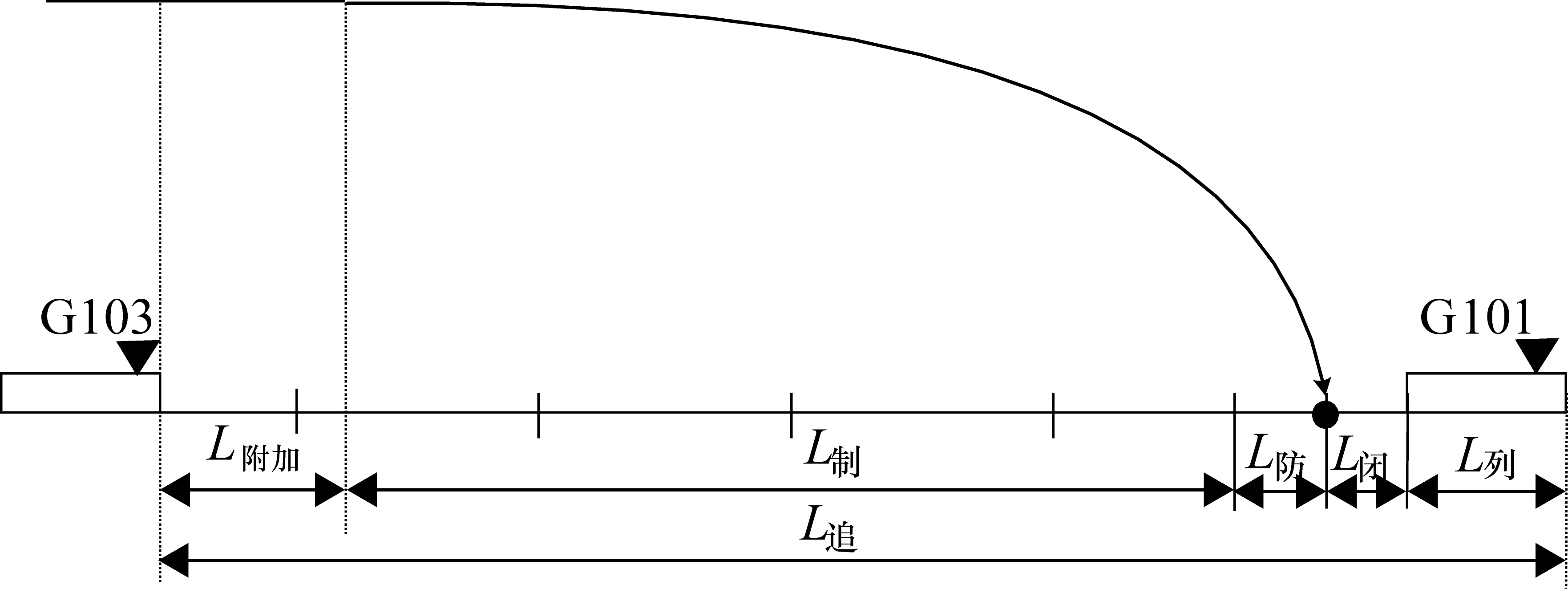
图3 列车区间追踪间隔运行图

2.2 基于分段迭代算法的制动距离多阶段划分

分段迭代算法的基本原理是将制动距离按一定的间隔距离分段进行计算，将上一阶段的动车组运行末速度作为下一阶段的运行初速度，计算每一段的动车组制动走行距离[11]。然后将各阶段的走行距离累加得到制动距离。通过牵引计算的分段迭代算法可得到动车组运行时间和运行距离的近似计算公式：

运行时间：

(2)

t=∑Δt

(3)

运行距离：

(4)

S=∑ΔS

(5)

式中，ζ=127/(1+γ)取决于回转重量系数γ；cp为Δt时间内的单位合力[12]。

同时按照分段迭代算法的阶段划分，建立动车组制动距离的基于动态规划算法的多阶段模型，动态规划的基本原理是将一个复杂的决策问题分解划分为n个阶段，从动车组追踪间隔时间的追踪点出开始，向后列车往后缩减防护距离进行多阶段的划分，其分段间隔必须与分段迭代算法的分段间隔一致，这样结合动态规划算法和分段迭代算法求解制动距离最优解。计算过程采用典型的动态规划算法的逆序原理，从后往前计算求解每一个分段内的制动走行距离最优解，同时从每一个阶段的备选方案中逆推得到每一阶段的坡度化简最优方案，最后将所有阶段的最优决策序列所求得的各子阶段最优解函数整合起来得到动车组制动距离的最优解函数[13-15]。

列车追踪间隔时间的计算公式为

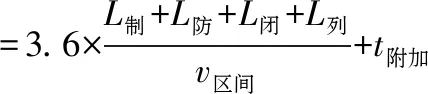
(6)

式中，3.6为单位换算系数；L防为安全防护距离，取110 m；L闭为闭塞分区长度，取1500 m；L列为列车长度，取8节编组的CRH380A型动车组长度为200 m；v区间为列车区间运行速度，取320 km/h;L制为列控车载设备监控制动距离，查找文献[16]～文献[18]得到CRH380A型动车组在制动初速度为320 km/h时的紧急制动距离应小于6300 m，取3600 m分段进行计算，并根据动态规划算法进一步优化；t附加的取值在CTCS-3条件下一般为14 s[16]。将制动过程划分为间隔距离为ΔS=400 m的n个阶段作为COADP算法的多阶段划分。动车组制动距离的多阶段划分如图4所示。

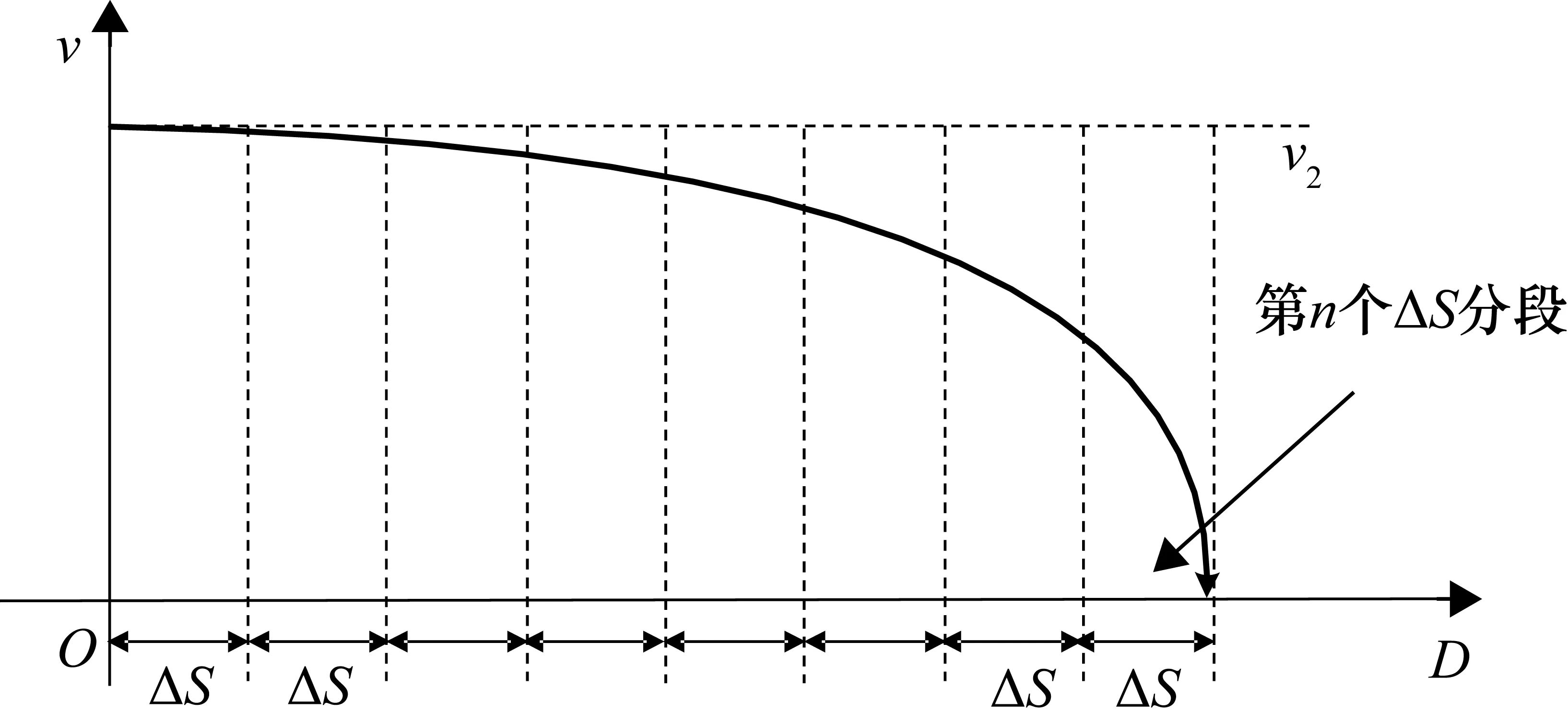
图4 分布迭代算法曲段划分示意图

列车制动距离的多阶段划分不仅关系到制动距离的计算，而且直接为后续的动态规划优化求解提供多阶段模型，两者必须完全契合才能进一步选取动车组非线性关系模型的阶段变量、状态变量和最优解序列以及最优解目标函数，最终得到制动距离的最优解[15]。以图3所示的列车区间追踪间隔时间图为例进行分段迭代算法的多阶段划分，并以此建立追踪间隔时间的多阶段决策模型，如图5所示。

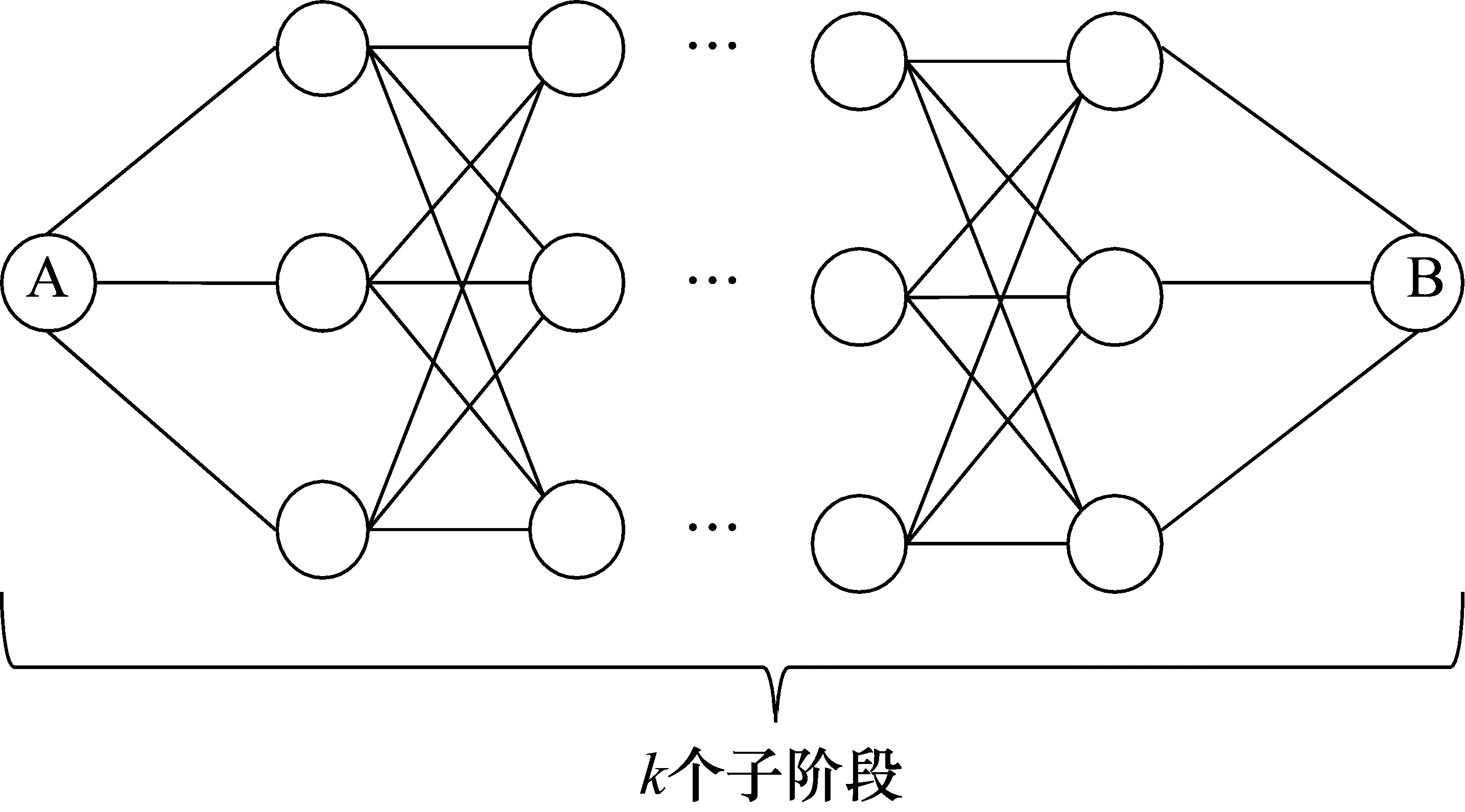
图5 多阶段决策模型示意图

3 基于COADP算法的过程求解

动车组制动距离的优化过程是一个非线性问题，因此可以通过以上的多阶段划分将优化过程看作在离散时域内的非线性关系模型[18]：

xk+1=F(xk,uk),k=0,1,2,…

(7)

COADP算法是基于ADP算法的一种优化算法，主要过程是将选取好的阶段变量xk和状态变量uk输入执行网络以及前面得到的动态系统的非线性关系模型得到下一个阶段变量的输入xk+1，得到此子过程的最优解函数J(xk+1)，然后再与前一阶段的决策变量U(xk,uk)比对，这样通过训练得到评判网络，然后在进行任意阶段的计算时，继续前面的过程，通过评判网络比较选取最优的状态变量xk+1，最后通过式(8)所示的最优决策变量得出式(9)所示的k子过程的最优解状态方程[17]。这样把划分好的各阶段都进行以上运算，递推得到全部各阶段的最优解函数，就得到了整个过程的最优解函数J(xk,uk)。

(8)

(9)

由于过程越复杂，动态规划算法的计算量越大，计算维数也越来越大，所以传统的动态规划算法容易形成“维数灾”，采用COADP算法对基于坡度化简的制动距离进行优化时，COADP计算过程分为n个进程，可以通过评判网络寻找得到各阶段的最优解，进而得到整个过程的最优解序列，既保证了多阶段序列的求解模型能够合理建立，也避免了传统的动态规划算法容易形成“维数灾”的问题。

图6为COADP算法的结构图，选取动车组速度作为动态规划算法的状态变量xk，制动过程开始后到列车追踪点的距离作为动态规划算法的阶段变量uk=(uk，uk+1，…)，性能指标函数即制动距离最优解函数为

(10)

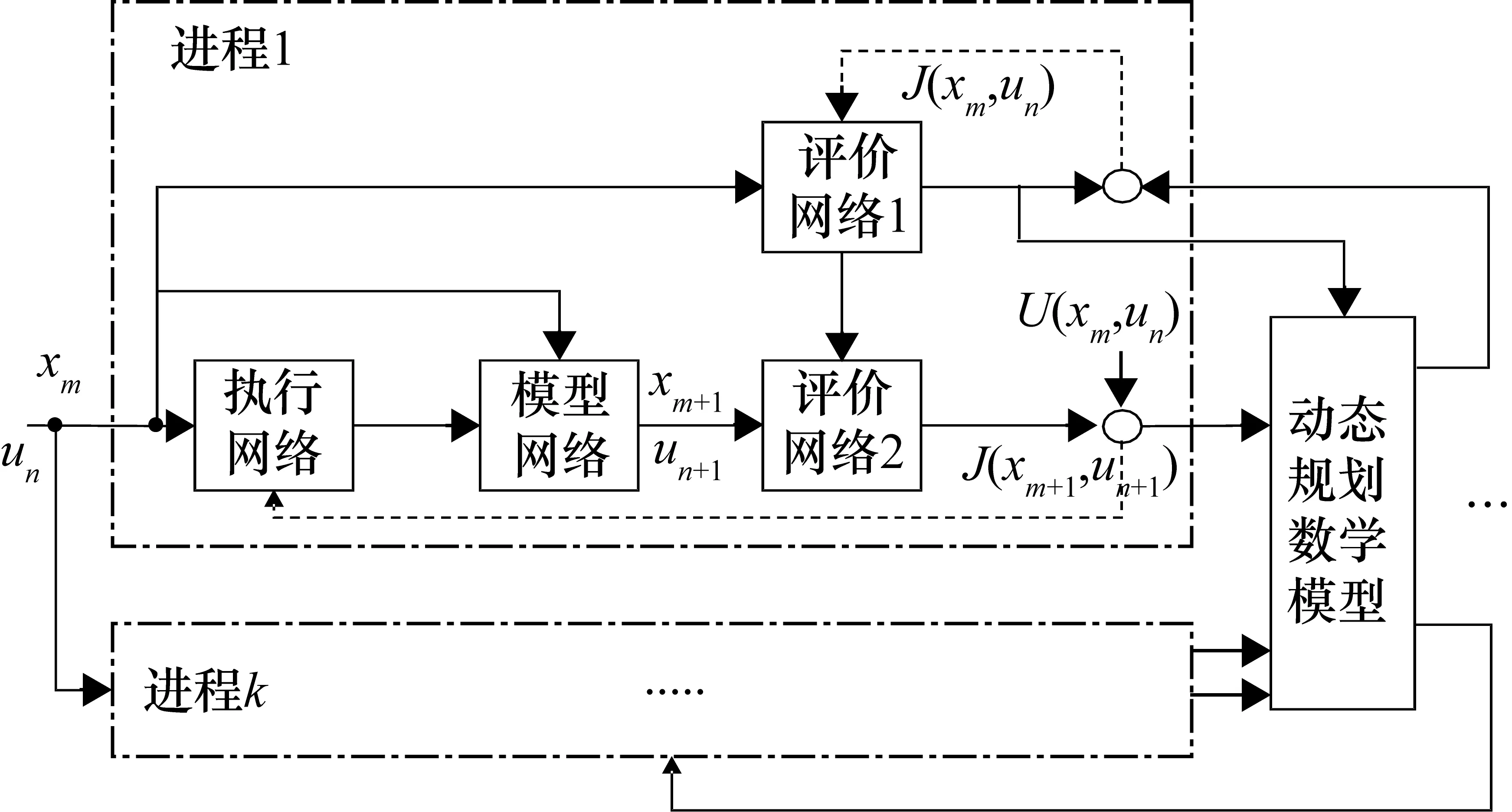
图6 COADP算法结构图

图7为COADP算法的流程图。由贝尔曼最优性定理[19]，得出式(11)所示的制动距离的最优性能指标函数的贝尔曼方程和式(12)所示的第k个子阶段的制动距离最优控制策略：

(11)

(12)

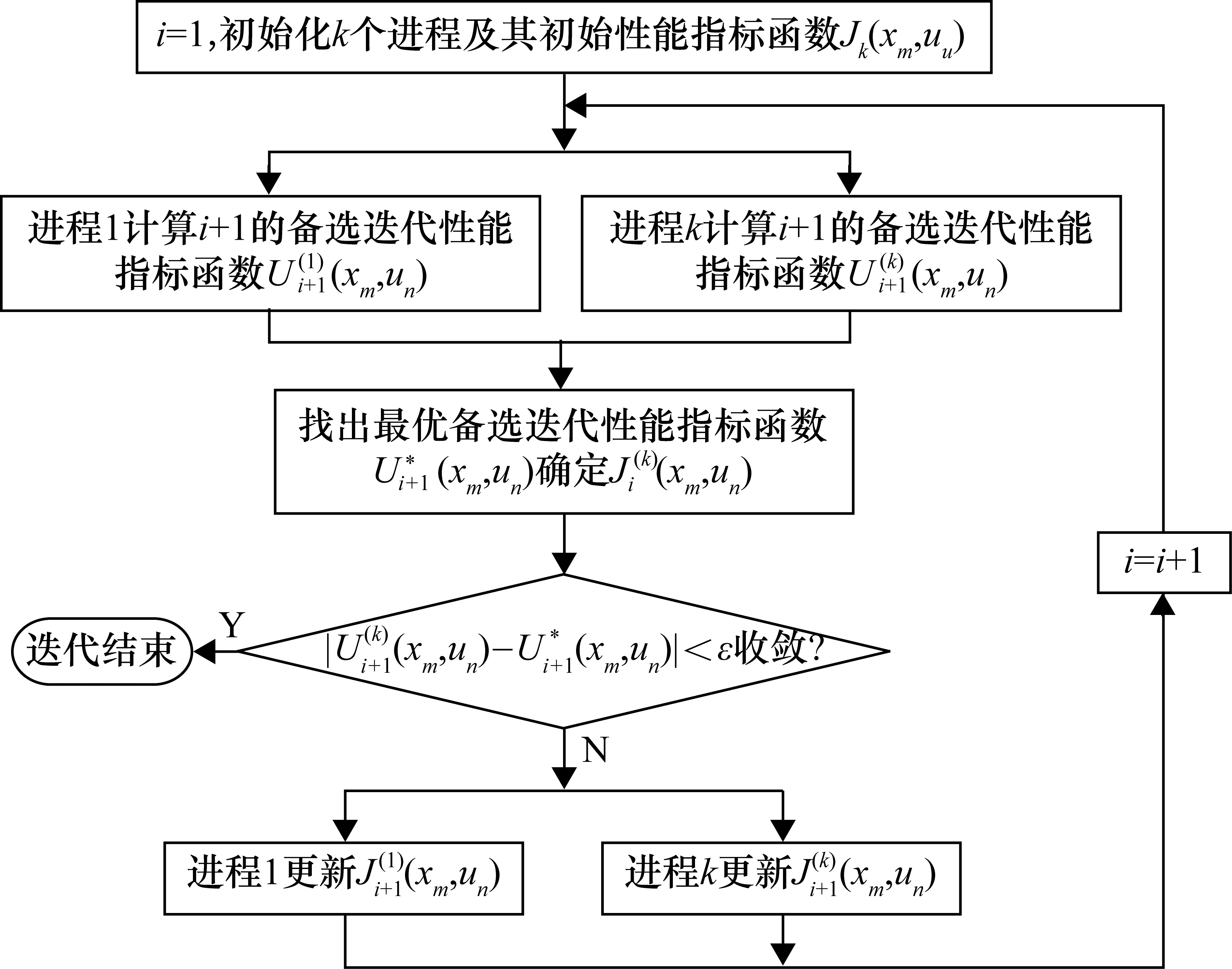
图7 COADP算法流程图

4 牵引计算仿真分析

4.1 运行阻力

以成渝高铁的部分线路数据作为实验数据，分别采用ADP和COADP在几个典型区段上两种算法对列车制动距离进行了仿真计算,以车辆编组为8节的CRH380A型动车组为例，动车组定员质量为429000kg[20]，通过式(13)和式(14)计算，可以得到在不同坡度上CRH380A型动车组的运行阻力为

W=10-3M(w0+wj)g

(13)

单位运行阻力为

w=w0+wj

(14)

式中，M为列车质量；g为重力加速度；w0为基本阻力；wj为附加阻力。

4.2 空气制动力

其他条件相同时不同类型的动车组单位空气制动力的大小是相同的，取320 km/h作为动车组运行的初始速度。常用制动时，β取0.75 m/s2，通过计算得到单位空气制动力为81.04 N/kN(N/kN表示列车单位重力的空气制动力)；紧急制动时，β取1.35 m/s2，通过计算得到单位空气制动力等于145.87 N/kN。

4.3 再生制动力

动车组采用空气制动和再生制动的复合制动模式，而且空气制动力是随着所需制动力和再生制动力的差值不断变化的，所以动车组的再生制动力并没有明确的计算方法。但是通过运行参数和经验，当动车组所需制动力没有超过再生制动力的阈值，那么动车组制动力全部由再生制动力提供，此时没有空气制动力；当动车组所需制动力超过了再生制动力所能提供的阈值，那么再生制动力不能提供的部分将由空气制动力提供。

4.4 算法仿真

通过C#和Microsoft Access平台的动车组牵引计算仿真系统，取320 km/h作为仿真计算的动车组制动初速度，由上述CRH380A型动车组参数仿真得出在两种算法下的列车制动距离的优化力度曲线如图8所示，COADP算法相比较传统的ADP算法能够对制动距离有显著的优化，而且能够更快速准确地找到各子阶段的最优解函数。

图8 两种算法对制动距离的优化曲线

两种算法下的列车制动距离的优化力度曲线如图8所示，COADP算法相比较传统的ADP算法能够对制动距离有显著的优化，而且能够更快速准确地找到各子阶段的最优解函数。图9为两种算法下得到的动车组制动时间曲线。

由图9所示的制动时间仿真结果可知，未优化的最小追踪间隔时间为224 s，由ADP算法得到的最小追踪间隔时间为198 s，由COADP算法仿真得到的最小追踪间隔时间结果为169 s，通过COADP算法优化得到的最小追踪间隔时间较优化前减少了55 s。图10和图11为优化前后动车组最小追踪间隔时间的仿真曲线，通过对最小追踪间隔时间仿真结果图的对比可以得出优化后的最小追踪间隔时间比优化前明显缩短，由此可见COADP算法对于高速铁路追踪间隔时间有显著的优化效果。

图9 两种算法对制动时间的优化曲线

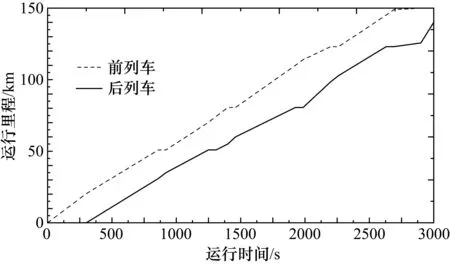
图10 优化前最小追踪间隔时间仿真图

图11 优化后最小追踪间隔时间仿真图

5 结束语

本文通过对线路坡度和列车长度的分析，建立了列车混合优化模型，通过对动车组的制动距离分为多个间隔区段，得到动态规划的多阶段模型，采用COADP算法对列车线路坡度化简方案进行逆推寻优，求解动车组制动过程内各阶段的最优阶段变量、最优状态变量、决策序列最优解以及制动距离最优解的指标函数，得到基于列车参数和线路坡度的追踪间隔时间最优解函数。有效避免了传统动态规划算法“维数灾”的问题，并对ADP和COADP算法的优化结果进行了仿真比对，结果表明COADP算法的优化力度更加明显。动态规划算法在列车追踪间隔时间方面的应用也对线路坡度的设计提供了更好的方案，对铁路运输能力和通过能力的提高具有重要的现实意义。