基于拉格朗日插值法的卫星导航空间信号精度评估算法
王尔申,赵 珩,曲萍萍,庞 涛,孙 军
(1.沈阳航空航天大学 a.电子信息工程学院;b.辽宁省通用航空重点实验室,沈阳 110136;2.中国人民解放军93798部队,沈阳 024413)
用户测距误差URE(User Range Error)是空间信号(SIS)精度的重要指标之一[1],SIS URE定义为导航卫星位置与钟差的实际值与利用预报卫星星历得到的预测值之差[2-4],其主要反映了导航星历和预报钟差的精度。URE能够综合反映控制段、空间段对精度的影响,进而反映卫星导航系统的系统性能,其主要取决于卫星的位置和钟差的精度[5-6]。目前的URE计算方法有网格法和高精度的激光角反射器测量评估法,但由于计算量较大和不能广泛分布等原因使这两种方法都未能得到广泛使用,其中激光测距法得到的数据可以减少卫星坐标与时钟的相互影响[7-9]。广播星历采用本地接收机采集到的2018年11月13-14日共48小时的GPS和BDS广播星历和IGS提供的GPS和BDS精密星历数据对GPS和北斗的空间信号精度进行了评估。
对于精密星历的处理,传统的拉格朗日插值方法虽然具有较高的精度,但是随着插值节点的增多,插值节点边缘的精度会急剧下降,并出现龙格现象。滑动式拉格朗日插值法处理精密星历具有较高的精度和插值效率,且其精度能够达到毫米级别[10-12]。文中采用10阶拉格朗日滑动式分段插值法对精密星历进行处理,基于以上方法得到的数据,使用分段式评估模型对GPS和北斗导航系统的空间信号精度进行了评估,其具有运算量小、精度高的优点。统计分析置信度为95%的GPS、BDS SIS URE、URRE(User Range Rate Error)、URAE(User Range Acceleration Error)。
1 SIS URE分段评估模型
SIS URE是指卫星位置和钟差的实际值和预测值之差。但由于卫星的真实位置无法获取,通常将事后精密星历中取得的卫星位置作为该时刻的真实卫星位置。通常用瞬时URE和置信度为95%的URE表示SIS URE[13]。当IURE~N(0,σ2),则95%URE=URE(1s)×1.96。
通过广播星历和精密星历,统计得出卫星轨道的R,A,C,T,得出SIS URE的分段式计算公式为
rmsUREGPS=
(1)
SIS rms UREBDS(MEO)=
(2)
SIS rms UREBDS(GEO,IGSO)=
(3)
其中,R、A、C分别为径向、切向、法向轨道误差;c为光速;T为钟差误差。
通过GPS的接口控制说明文档中的计算公式,计算出GPS在地心地固(ECEF)坐标系下的坐标。由于IGS提供的精密星历时间间隔为15 min和5 min,无法满足间隔30s的采样率,因此通过10阶拉格朗日插值法对精密星历进行内插,以得到与广播星历对应时间节点的真实卫星位置。考虑到由于插值节点增多带来的龙格现象,文中选取10阶滑动式拉格朗日插值法,取待插节点的前后各5组精密星历数据作为插值区间,相比于其他算法,具有精度高、运算量小等特点[10]。拉格朗日插值法的表达式为
(4)
其中,t为待插时间节点;t0,t1,t2,…,tn为n+1个待插值时间节点;y0,y1,y2,…,yn是与n+1个待插值时间节点对应的精密星历轨道误差和钟差分量。
选取部分数据,根据传统的拉格朗日插值法进行数据内插,得到结果如图1所示。

图1 传统拉格朗日插值法
从图1可以看出,龙格现象对插值方法的影响主要集中在前后三个内插节点。对PRN21采用间隔30 min数据作为已知点,对间隔15 min的数据根据滑动拉格朗日插值法进行插值,得到结果如下:

图2 GPS PRN21精密星历插值精度
从图2可以看到,对GPS精密星历插值结果中,在x、y、z方向上的插值精度基本均优于50 mm,满足高精度的使用需求。
在此基础上,得到对应的R、A、C误差
ECI=R(θ)·ECEF
(5)
ECI=R(θ)·CGCS2000
(6)
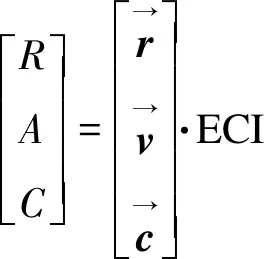
(7)
其中,ECI表示卫星在惯性坐标系下的轨道误差;ECEF为在GPS卫星在地心地固坐标系下的卫星轨道误差;r为卫星速度在卫星到地心连线方向单位向量;v为卫星速度在切向上的单位向量;c为垂直于轨道面的法向单位向量。
2 SIS URE数据处理与结果分析
(1)广播星历解析
广播星历使用本地接收机接收到的实测数据,仿真时间为2018年11月13日-14日。将GPS和BDS广播星历中得到的星历参数分别代入GPS和北斗接口控制文件提到的相关模型中[14],可计算得到GPS和北斗分别在地心地固坐标系和北斗坐标系下的轨道位置和钟差。
(2)卫星真实位置获取
文中使用的GPS精密星历是通过IGS(时间间隔为15 min)获取,精密星历具有精度高的特点,因为需要事后获取,因此不具有实时性。IGS提供的精密星历定位精度可达到5 cm左右,钟差精度优于1 ns,达到0.2~0.8 ns,因此一般将事后精密星历作为卫星的真实位置[11]。利用式(3)~(4)获得与广播星历对应时刻的卫星真实位置和钟差。
(3)SIS 轨道误差及钟差误差计算
可以直接通过上述方法来计算GPS和BDS在仿真时段内的SIS的径向、切向、法向轨道误差和钟差误差。在计算轨道误差和钟差误差时需要解决以下几个问题:
① 地心地固坐标系、北斗坐标系与轨道坐标的转换。GPS和BDS通过广播星历计算得到的卫星位置属于地心地固坐标系和北斗坐标系,在后续计算中涉及到地心地固坐标系与轨道坐标R、C、A之间的转换问题。
② 剔除计算过程中的明显粗差。在处理实测广播星历数据时,计算得到的轨道误差、钟差等数据波动较大,会出现较明显的粗差,需要在对数据预处理的过程中剔除掉;例如广播星历中卫星轨道数据标识为“不健康”、精密星历中出现的不正常的坐标和钟差等。此外,在计算卫星位置过程中会有一些标识为“健康”的卫星,但对其计算得到的结果可能会包含粗差,这些也需要剔除。
使用式(5)~式(7)分别对GPS和BDS SIS URE进行计算和统计,得到结果分别如图3和图4所示。
由图3可知,2018年11月13日-14日可观测到的GPS卫星中,除PRN4始终无法观测到和另外几颗卫星的样本数据较少无法得出统计数据外,PRN1、PRN19和PRN23都大于2.5 m,其中PRN1的URE最大,接近3.5 m;其余卫星的SIS URE均低于2 m,均优于GPS标准性能文件中的指标。受到径向误差的影响,使部分卫星的SIS URE偏大,因此卫星的径向经度对SIS URE有重要影响。

图3 GPS SIS URE(95%置信度)
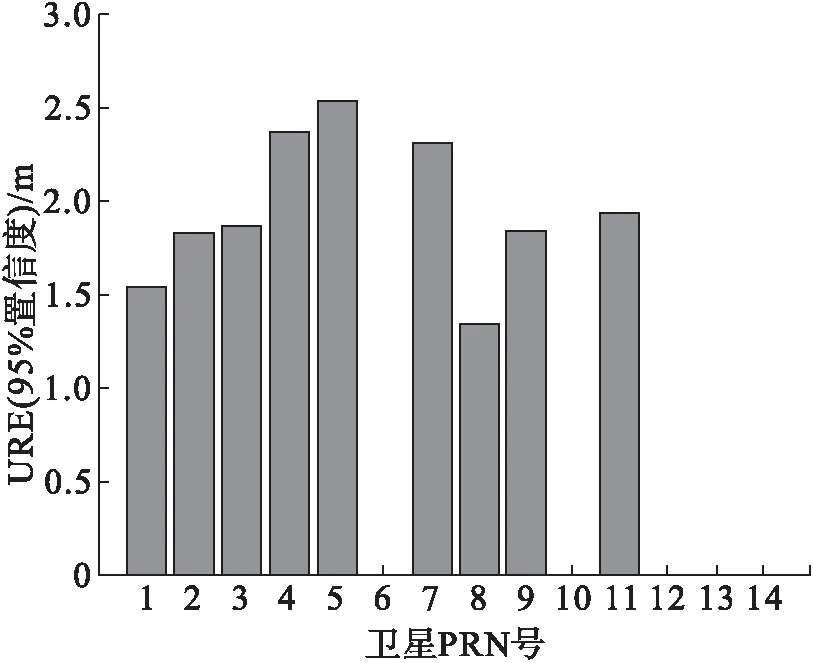
图4 BDS SIS URE(95%置信度)
图4为BDS SIS URE,从图中可以看到部分卫星样本较少无法得到统计数,C4、C5、C7的URE均大于2 m,其中C5略大于2.5 m;其余卫星均小于2 m,符合北斗标准性能服务规范中的指标。
3 SIS URRE、URAE结果分析
大量研究表明,卫星时钟的不稳定会引起较大的URRE和URAE误差,时钟的不稳定性将直接反映在URRE和URAE中,其误差可达到轨道误差的10倍以上。常用的计算卫星SIS URRE和SIS URAE有差分法和载波法,由于这两种传统方法均存在一定局限性,而高稳定度振荡器的频率稳定度的时域表征目前均采用Allan方差,因此本文采用交叠式Allan方差法来评估卫星的URRE和URAE。
Allan方差基本原理:设系统采样周期为τ,连续采样N个数据点X(i),i=1,2,3,…,N。将其每按M个点进行分组,则每组时间内各点的均值序列Y(k) 为
(8)
从而差值序列D(k)为
D(k)=Y(k+M)-Y(k),k=1,2,…,N-2M+1
(9)
交叠式Allan方差表达式如下所示,其〈〉表示求取均值
(10)
文中以计算得到的钟差作为初始样本,使用式(8)~(10),得到SIS URRE和SIS URAE,并统计得到仿真时段内置信度为95%的SIS URRE和SIS URAE数据,如图5和图6所示。

图5 GPS SIS URRE(95%置信度)
由图5可以看到,除PRN4在仿真时段内始终没有被接收机观测到外,其余所有GPS卫星的SIS URRE均小于0.006 m/s,均优于GPS SPS PS(2008)中的指标。

图6 GPS SIS URAE(95%置信度)
由图6可以看出,除了由于换星等因素使PRN8和PRN24的SIS URAE偏大外,所有GPS可见卫星的SIS URAE均优于GPS PS SPS(2008)0.002 m/s2的指标。
利用式(8)~式(10),对BDS的URE数据进行计算和统计,得到如图7~8所示的BDS SIS URRE和URAE。

图7 BDS SIS URRE(95%置信度)
由图7知,在仿真时段内所有可见BDS卫星的SIS URRE均小于BDS接口文件中所规定的标准0.006 m/s。
由图8可知,在仿真时段内所有可见BDS卫星置信度为95%的SIS URAE均小于BDS接口文件中所规定的标准0.002 m/s2的指标。

图8 BDS SIS URAE(95%置信度)
4 结论
文中采用滑动式拉格朗日插值法对精密星历进行处理,仿真验证了滑动式拉格朗日插值法的精度。并根据本地接收机实测广播星历数据对2018年11月13日-14日的GPS和北斗实测数据的SIS URE精度进行了仿真验证,仿真分析结果表明:在GPS可见卫星中,除PRN1、PRN19和PRN23三颗卫星的SIS URE大于指标数值外,其余GPS卫星的SIS URE均优于指标数值。对于BDS SIS URE,除C4、C5、C7外,其余卫星的SIS URE均优于接口文件中的指标。GPS SIS URRE和URAE均优于指标数值。

