四旋翼无人机执行器故障下的饱和容错控制
关 威,史 沛,任 艳
(沈阳航空航天大学 自动化学院,沈阳 110136)
由于在质量、体积、机动性等多方面的优势,四旋翼无人飞行器越来越多地被应用在军用或民用等方面,为我们的社会和生活带来了很多的方便[1]。但是四旋翼无人机是一个拥有多个输入和多个输出的复杂被控对象,它的状态变量多、强耦合的特性,造就了其在飞行过程中需要更精确和更有效的控制策略。近年来关于无人机故障、容错控制、自适应控制的研究越来越多,文献[2-4]分别对这些研究做了简单的归纳总结。根据故障发生的位置不同,可以将四旋翼无人机的故障类型分为执行器故障、传感器故障和系统故障。在故障容错控制方面,主要有反步法[5]、模型预测[6-7]、PID控制[8]反馈线性化、鲁棒控制[9]等。所以,四旋翼无人机的安全性问题越来越受到人们的关注,如何提高其在飞行过程中的容错控制能力[10-11]并且使其具有更好的抗干扰能力成了现在的研究热点,具有很好的研究意义。
在日常生活中,执行器饱和和故障[12]都是我们经常遇到的现象,并且存在于很多运行的系统中。这种背景下,本文同时考虑四旋翼无人机执行器饱和和故障问题,并且基于线性矩阵不等式的方法设计了一种自适应控制器的设计方法。该控制器采用自适应率在线调节自适应参数的方法来实现对无人机执行器的控制,并且通过Matlab仿真实验来验证算法的有效性。
1 模型建立
四旋翼飞机通过调整电机转速来调整其位置和高度,从而实现轨迹跟踪。该模型如图1所示,通过牛顿-欧拉运动定理,简化的系统模型如下[13]。
其中,x,y,z分别表示飞行器重心在惯性坐标系中的位置。滚转角度、俯仰角和偏航角分别用Ebx,Eby,Ebz表示。飞机质量用m表示,I是物体重心与螺旋桨轴线之间的距离,非线性项:
Ua=(cosEbxsinEbycosEbz+sinEbxsinψEbz)
Ub=(cosEbxsinEbycosEbz-sinEbxcosEbz)
Hx,Hy,Hz代表飞行器绕x,y,z轴的转动惯量。令
作为模型的不确定性,g是重力加速度。
K(.)是系统的气动阻尼系数,d(.)表示未知的外部干扰,τf,τEbx,τEby,τEbz分别表示系统的总升力、滚转力矩、俯仰力矩和偏航力矩。
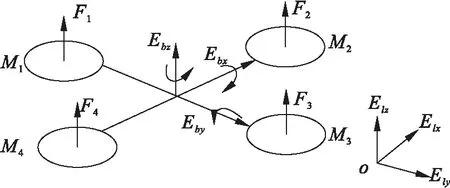
图1 四旋翼飞机模型图
本文将飞机模型分解为Σ1和Σ2两个子系统。
其中u(v1)=[u(τEby)u(τEbx)]T,u(.)表示约束后的控制量,Td1是位置子系统中由气动干扰和未知外部干扰组成的复合扰动。Td2表示姿态子系统,不受外界干扰。模型中每个状态变量和系数矩阵的含义是

其中,u(v2)=[u(τf)u(τEbx)]T,Td3是系统复合干扰项。模型中每个状态变量和系数矩阵的含义是
对于飞机的运动方程,假设参考(不受扰)运动是一种对称、稳定的线性运动;其纵向运动状态向量为n={v,c,p,l}T,控制输出是u={WE,Wc}T,飞机纵向运动模型可表示为:
2 控制器设计
2.1 问题描述
考虑如下形式线性时不变系统
z(t)=Cx(t)+Dn(u)
(1)
其中x(t)∈Rn为系统状态,n(t)∈Rm为带有饱和现象的系统控制输入,z(t)∈Rs为参考输出,ω(t)∈Rd为L2[0,]形式的外部扰动
描述故障模型[14-15]:
uF(t)=(I-d)n(u(t)),d∈{d1…dL}
(2)
其中d=diag[d1,d2…dm]。
2.2 控制器设计
考虑如下形式的带有执行器故障(2)及执行器饱和现象的系统
z(t)=Cx(t)+D(I-d)n(u(t))
(3)
选择如下结构的控制器
(4)

四旋翼无人机系统在饱和时的线性表达如下:
(5)
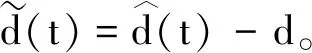
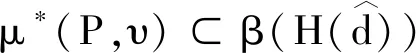

(6)
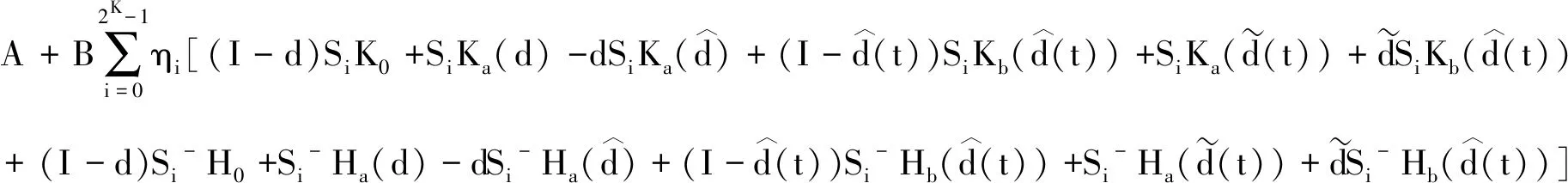
定理[16]:如果存在矩阵X>0,d0,daj,dbj,y0,yaj,ybj,j∈I[1,k]和对称矩阵qi,i∈I[0,2K-1]如下不等式成立

(7)
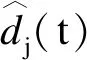
(8)
其中
L1j=-LjxP(t)

Kbj=ybjX-1,Haj=dajX-1,Hbj=dbjX-1.
Lj>0(j∈I[1,k])且ν>0,为自适应律增益,该增益可根据实际情况进行选择。进而得到相应的控制器增益为
(9)
所以,为了获得最小的指标rn和rf和最大化扰动容许水平v,我们使用了下面的最优化方法。
minη=αηn+βηf+γηv
s.t.(a) (7),
(10)
其中
且α,β,γ为加权系数。然而,条件(b)不能够以线性矩阵不等式的方式直接表示出来。显然,μ*(P,ν)⊂μ(P,ν),这说明条件(b) 可由条件(b1) 替换。
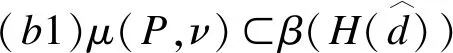
(11)
条件(b1) 等价于,对所有j∈I[1,k]
(12)

其中dajs为daj的第s行,且s∈I[1,k]。
3 仿真算例
四旋翼无人机系统状态方程参数如下

考虑下面系统的两种模式:
正常模式:d1=0
故障模式:0≤d2≤α,α表示最大的失效率。
我们考虑系统的H性能。给出如下形式的扰动

图2表示正常模式下,系统在自适应控制器作用下的第一个状态和第三个状态的状态响应曲线。
图3表示当系统故障,系统在两种不同控制器作用时的第三个状态的状态曲线。
由图2和图3我们可以明显看出,在两种情况中,本文提出的自适应H控制器比以往的固定增益H控制器对系统具有更好的控制效果,证明了我们提出的自适应控制器设计方法的优越性。

图2 正常模式下,系统在自适应控制器作用下响应曲线
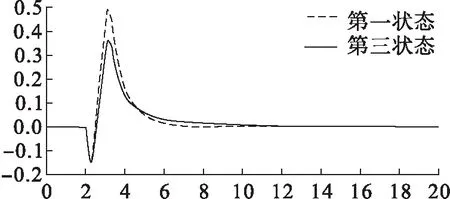
图3 系统第三个状态在故障模式下的响应曲线
4 结论
本文针对四旋翼无人机执行器故障下的饱和容错控制进行了研究。首先建立了四旋翼无人机的动力学模型,针对饱和的线性时不变系统,提出了一种自适应容错H∞控制器的设计方法。这种方法是在线性矩阵不等式(LMI)的基础上提出的,能够保证闭环系统在执行器饱和和执行器失效情况下的自适应H∞性能。通过进行仿真实验验证了我们提出的自适应容错控制器设计方法的有效性。

