基于切片二维图像的血管三维重建研究

(1.陕西服装工程学院经济管理学院；2.陕西服装工程学院基础部，陕西西安，712046)

引言

三维重建是指用切片机连续不断地将样本切成数十、数百的平行切片，依次逐片观察后，根据拍照并采样得到的平行切片数字图像，运用计算机来重建组织、器官等准确的三维形态。本文是基于切片二维图像的血管三维重建研究，主要目的是为了得出三维图像。现着重解决以下问题：

问题1，研究如何求出血管半径的方法，并求出血管管道半径。

问题2，根据问题1研究求管道的中轴线的计算方法，并求出管道中轴线的数学模型函数关系式。

问题3，根据问题1、问题2研究如何绘制管道的中轴线分别在XY,YZ,ZX平面的投影图，再根据这些平面投影图研究如何绘出制血管管道的三维立体图像。

1 问题分析

根据题中所给的图片立体想象出血管的变动情况，本文的难点是由于血管不是类似于圆柱体的有规则图形，而是一个无规则图形，为了计算更精准，在计算血管半径时利用每一张切片的内切圆求平均值。

1.1 问题1分析

1.2 问题2分析

首先，通过问题1模型的建立和求解，得出100张切片内切圆的圆心坐标，将这些坐标导入Excel表格中，通过MATLAB软件对坐标进行处理得出一个散点图；然后，根据这个散点图拟合出多个函数图象，将这些函数图像做比较从中挑出最优函数，挑出的最优函数为三角函数；最后，得出管道中轴线的数学模型函数关系式为：

1.3 问题3分析

首先，通过问题1模型的建立和求解，得出100张切片内切圆的圆心坐标，将这些坐标导入Excel表格中，利用MATLAB软件绘制管道的中轴线分别在XY,YZ,ZX平面的拟合函数图形；然后，通过MATLAB软件编程得到管道的中轴线分别在XY,YZ,ZX平面的投影图；最后，绘制出血管管道三维重建的三维立体图像。

2 模型的建立与求解

2.1 问题1的解决方案

首先，将图中所给的第一张切片导入MATLAB软件中；然后，利用MATLAB软件编程求出第一张切片的半径；接着，按照求第一张切片方法接的剩余99张切片半径；最后，求出100张切片半径的平均值，这个平均值即为血管管道半径。

2.1.1 问题1模型的建立

对题中所给信息进行分析，由于题中所给的信息有限，为了使所求半径更接近实际值，可根据每一个切片半径来求血管管道的半径。故本文将100个切片分开处理。

图6 转至前第一张切片的0-1矩阵局部图

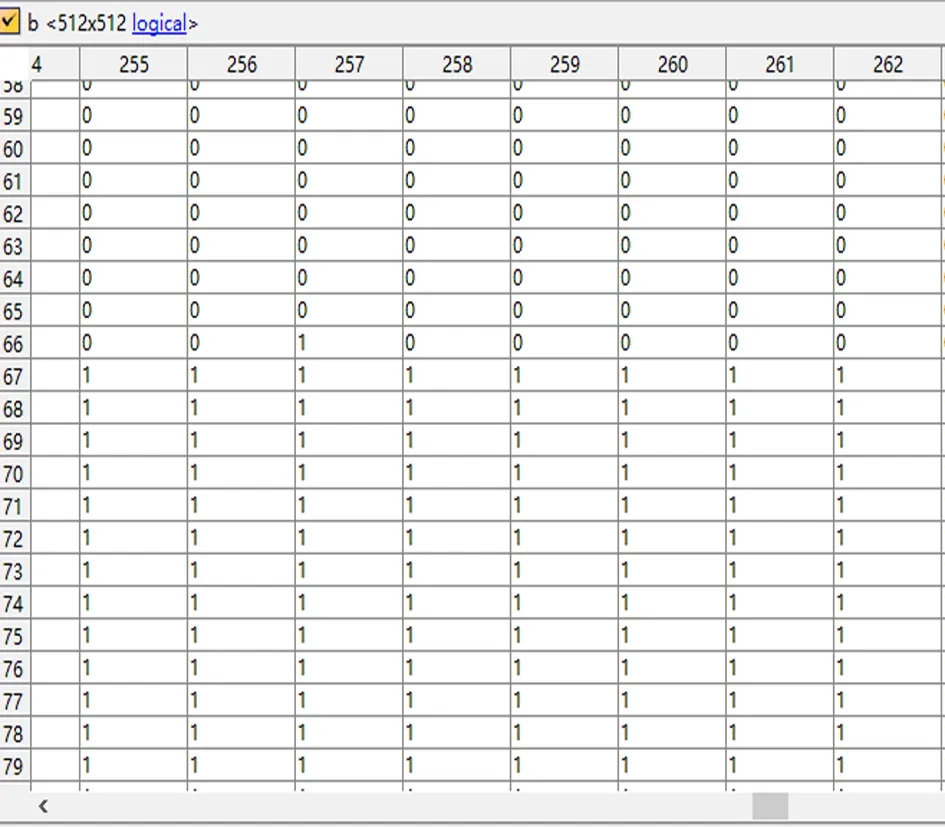
图2 转至后第一张切片的0-1矩阵局部图

图3 第一张切片骨架的0-1矩阵局部图

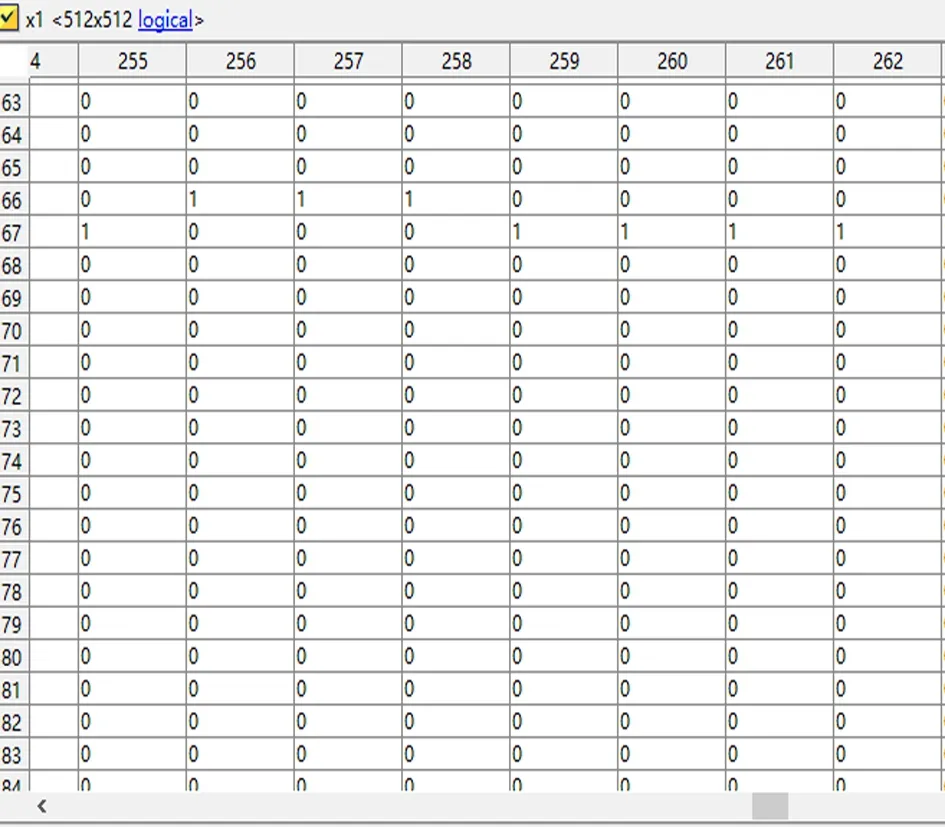
图4 第一张切片轮廓的0-1矩阵局部图

两点之间距离公式为：

表1 第一张切片骨架中所有点到轮廓上所有点的距离排序

11.41422...35.051735.12831.41422.23612.8284...38.470838.60052.236133.1623...41.677341.7852︙︙︙2929.017229.0689...68.264268.359329.068929.154829.2746...68.359368.4690

表2 第一张切片骨架任一点到轮廓所有点最短距离

min11.41422.2361…2929.0689

根据表2，选出最短距离中的最大距离，作为第一张切片的半径大小ik。

接着，按照上述方法分别求出剩余的99张切片的半径，在解得切片半径的同时可以利用MATLAB软件得出切片内切圆的圆心坐标。

表3 100张切片半径及最大内切圆圆心坐标

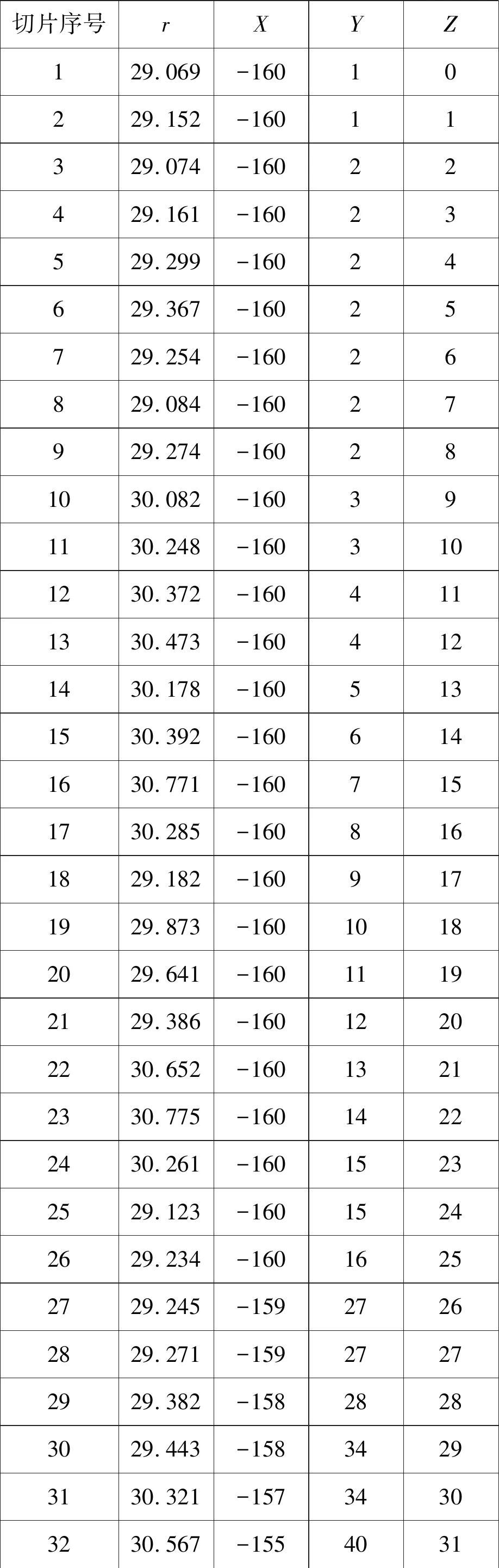
切片序号rXYZ129.069-16010229.152-16011329.074-16022429.161-16023529.299-16024629.367-16025729.254-16026829.084-16027929.274-160281030.082-160391130.248-1603101230.372-1604111330.473-1604121430.178-1605131530.392-1606141630.771-1607151730.285-1608161829.182-1609171929.873-16010182029.641-16011192129.386-16012202230.652-16013212330.775-16014222430.261-16015232529.123-16015242629.234-16016252729.245-15927262829.271-15927272929.382-15828283029.443-15834293130.321-15734303230.567-1554031

最后，为了使得血管管道半径更加精确，应求出这100个半径的平均值。平均值计算公式如下：

将100 张切片的半径代入公式2中，求出100个半径的平均值大小ωe。

2.1.2 问题1模型建立的步骤

综上所述，问题一的具体实现步骤可以总结如下：

2.2 问题2的解决方案

首先，在问题1模型的建立和求解的同时得出100张切片内切圆的圆心坐标；然后，将这些坐标导入Excel中，通过MATLAB软件拟合出曲线图；最后，得到管道中轴线的数学模型函数关系式。

2.2.1 问题2模型的建立

首先，对表3进行观察发现，在问题一模型的建立与求解中已经得出100张切片内切圆圆心坐标。

其次，将这些坐标导入Excel表格中，通过MATLAB软件对坐标进行处理得出一个散点图，并根据这个散点图拟合出多个函数图象。图5、图6、图7是拟合得出最接近散点图的指数函数和三角函数图像。经过对上图的观察，图7最接近散点图，所以我们选取三角函数为最优函数。

图5 指数函数图像

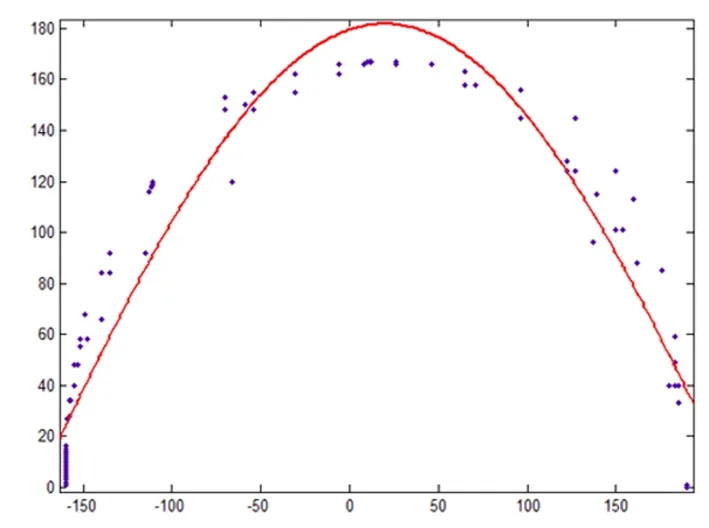
图6 指数函数图像

图7 三角函数图像

最后，根据散点图拟合得到的三角函数数学模型中的三角函数关系式

2.3 问题3的解决方案

要求绘制管道的中轴线分别在XY,YZ,ZX平面的投影图。首先，在问题1模型的建立和求解的同时得出100张切片内切圆的圆心坐标，将这些坐标导入Excel中，绘制管道的中轴线分别在XY,YZ,ZX平面的拟合函数图形；然后，再通过编程得到分别在XY,YZ,ZX平面投影图；最后，绘制血管管道的三维立体图像。

2.3.1 问题3模型的建立

首先，将表3中100张切片的内切圆圆心坐标导入Excel表格中，利用MATLAB软件绘制管道的中轴线分别在XY、YZ、ZX平面的拟合函数图形，再通过MATLAB软件编程得到分别在XY、YZ、ZX平面投影图。图8至图13分别为XY、YZ、XZ的平面的散点图和拟合函数图以及中轴线在XY、YZ、XZ平面的投影图,再根据这些图得到三维立体图像。

图8 XY平面的散点图及拟合函数图

图9 中轴线在XY平面的投影图

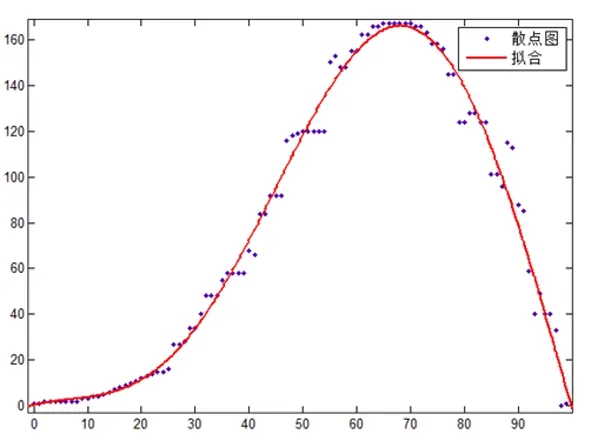
图10 YZ平面的散点图及拟合函数图

图11 中轴线在YZ平面的投影图

图12 XZ平面的散点图及拟合函数图

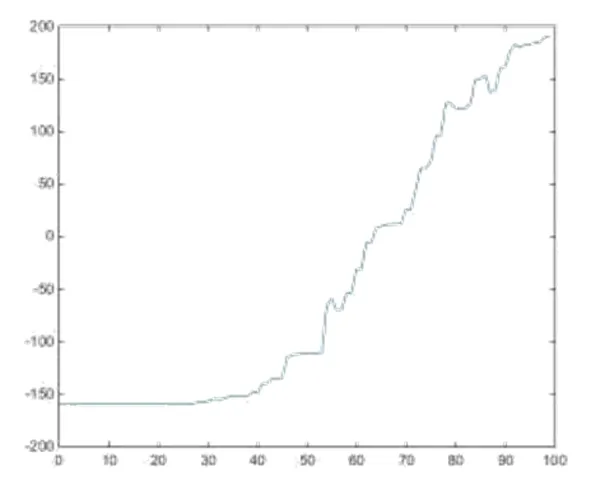
图13 中轴线在XZ平面的投影图

图14即为本文所求的血管三维重建的三维立体图形

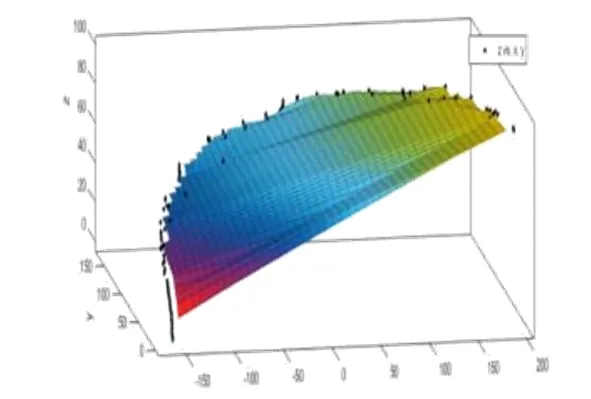
图14 血管管道的三维立体实体

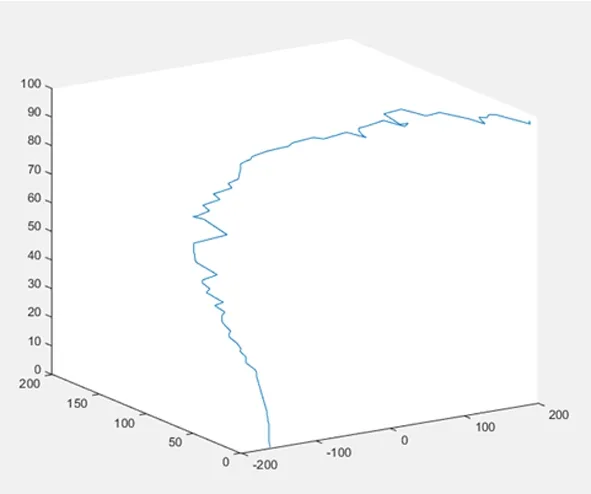
图15 血管管道的三维立体散点

3 结束语

(1)本文使用MATLAB软件编程建立模型，利用了平均值求解，平均值的计算能直观的反映数据的基本特征，使得到的结果精确度更高。

(2)在求管道中轴线的函数表达式时，利用多个拟合函数进行对比，最后选取最优函数,使得所得结果更加精准。

(3)模型可操作性强，适用范围广泛，不仅可以运用在血管三维重建中，还可以运用在科技[3]，医学，生物体的三维重建研究中。