相界面及相变晶体学择优

顾新福，石章智，陈 冷，杨 平

(北京科技大学材料科学与工程学院，北京 100083)

1 前 言

界面是多晶体材料中重要的微观组织特征之一。界面处的原子种类或结构往往不同于晶体内部的原子排列，界面上这些原子结构不仅在晶体的一系列物理化学过程中起到重要作用，并且对材料整体性能也具有很重要的影响[1]。

界面的存在会导致体系的吉布斯自由能增加，因而在固态相变时，新相与母相之间产生的界面是形核时的阻力项。为了降低形核能垒，两相之间易于形成特殊的低能界面取向[2]。因此，新相与母相之间常形成可重复的位向关系、界面取向及界面结构等晶体学特征，即存在相变晶体学择优现象[3, 4]。与相变热力学及动力学一样，相变晶体学也是理解材料组织不可缺少的知识[5]。

由于相变时界面倾向于形成低能界面，而低能界面通常具有特殊的界面结构，因此从界面结构入手分析常常是分析相变晶体学择优规律的重要方法[3, 4, 6-9]。本文旨在介绍相变晶体学几何模型的一般思想和处理方法，建立界面结构与相变晶体学择优的关系。文中首先介绍界面的基本定义，接着介绍处理相变晶体学择优问题的简单而直观的方法，再介绍定量的分析方法及其衍生模型，最后结合笔者近年开发的相变晶体学软件介绍应用实例。

1.1 界面几何

定义平直界面通常需要5个宏观参量，称为5个自由度。其中3个参量定义界面两侧晶体在空间的位向关系，剩余2个参量定义界面取向。

位向关系是指两晶体在空间中的位置关系。描述晶界时，常用轴角对表示位向关系。其中轴向由两个参数定义，绕轴的旋转角为另外一个参数，可见位向关系需要3个参数来描述。然而描述相变时，常用米勒指数表示位向关系，即用面和面平行及面内的方向和方向平行的关系来描述，这种表示方法比较直观。例如钢铁材料中的马氏体相变，马氏体(bcc)和奥氏体母相(fcc)之间的Nishiyama-Wasserman(N-W)位向关系可以近似描述成密排面平行(111)fcc//(011)bcc，近密排方向平行[1-10]fcc//[100]bcc。当然，两相之间的位向关系也可用轴角对或欧拉角等方式描述，它们之间可以通过位向关系矩阵相互转换。位向关系矩阵是将同一矢量从一晶体坐标系转到另一个晶体坐标系的变换。

界面如果是宏观的平面，面法向需要两个参数来定义。界面上可能包含位错和台阶等微观亚结构，因此可以根据界面结构对界面进行分类。

1.2 界面结构

根据晶体界面两边原子的匹配或对应关系，相界面可分为完全共格、半共格和非共格界面[2]，如图1所示。

图1a中的界面为完全共格界面。晶体α和晶体β的原子在界面上一一对应。此时两相晶格之间的错配非常小，界面处可以通过较小的应变实现完全共格，例如高锰钢中的ε马氏体与奥氏体(γ)之间的界面(0001)ε//(111)γ。这类界面的界面能通常较低。由于两相之间的弹性能与错配的平方成正比，随着两相晶格之间的错配增大，达到一定临界错配值之后，界面将丧失共格状态，界面的错配将通过周期性的位错来松弛，如图1b所示，这样的界面被称为半共格界面。位错与相邻位错之间是共格区。钢铁、钛合金和镁合金中多种析出相的界面就是半共格界面。当两相错配更大时，形成非共格界面，如图1c所示。非共格界面上不存在共格区和规则的共格点，此类界面的界面能较大。当然，在大错配时，两相之间也可以形成近似重合位置点阵的结构，或称为规则共格界面[5]，例如镁合金中的Laves相与基体之间的界面[10]。

图1中给定的界面均为原子级平界面，实际系统中的界面不仅包含位错，还包含台阶结构，称为结构台阶。图2是界面一侧的台阶结构图，由台面-侧面-扭折(terrace-ledge-kink, TLK)模型描述，其中台阶的台面、侧面和扭折的面均为晶体中的密排或次密排面。由于存在台阶，宏观界面的平均取向将偏离低指数晶面。如果界面指数不能用低指数表示，则称为无理界面。界面上的这些台阶称为本征台阶，实际起到松弛界面错配的作用。对于一般的系统，界面两侧的错配不能完全通过台阶松弛，一般界面上除了台阶结构之外还包含位错结构。

界面是位向关系和界面取向的5元函数，择优低能界面是这五维空间中的能量谷点(奇异点)。处于奇异点的界面又被称为奇异界面[1]。相变晶体学几何模型大多基于界面上原子或晶格的匹配或错配分析，然后根据某种匹配好的准则或者判据限制界面取向及位向关系[3, 4, 6, 8]。因此，分析界面原子匹配对理解这些晶体学择优规律至关重要。下一节将介绍匹配的定义以及寻找界面上匹配好区的方法。

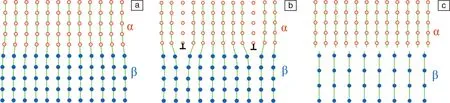
图1 相界面类型：(a)完全共格，(b)半共格，(c)非共格Fig.1 Types of interphase boundary: (a) coherent, (b) semi-coherent, (c) incoherent

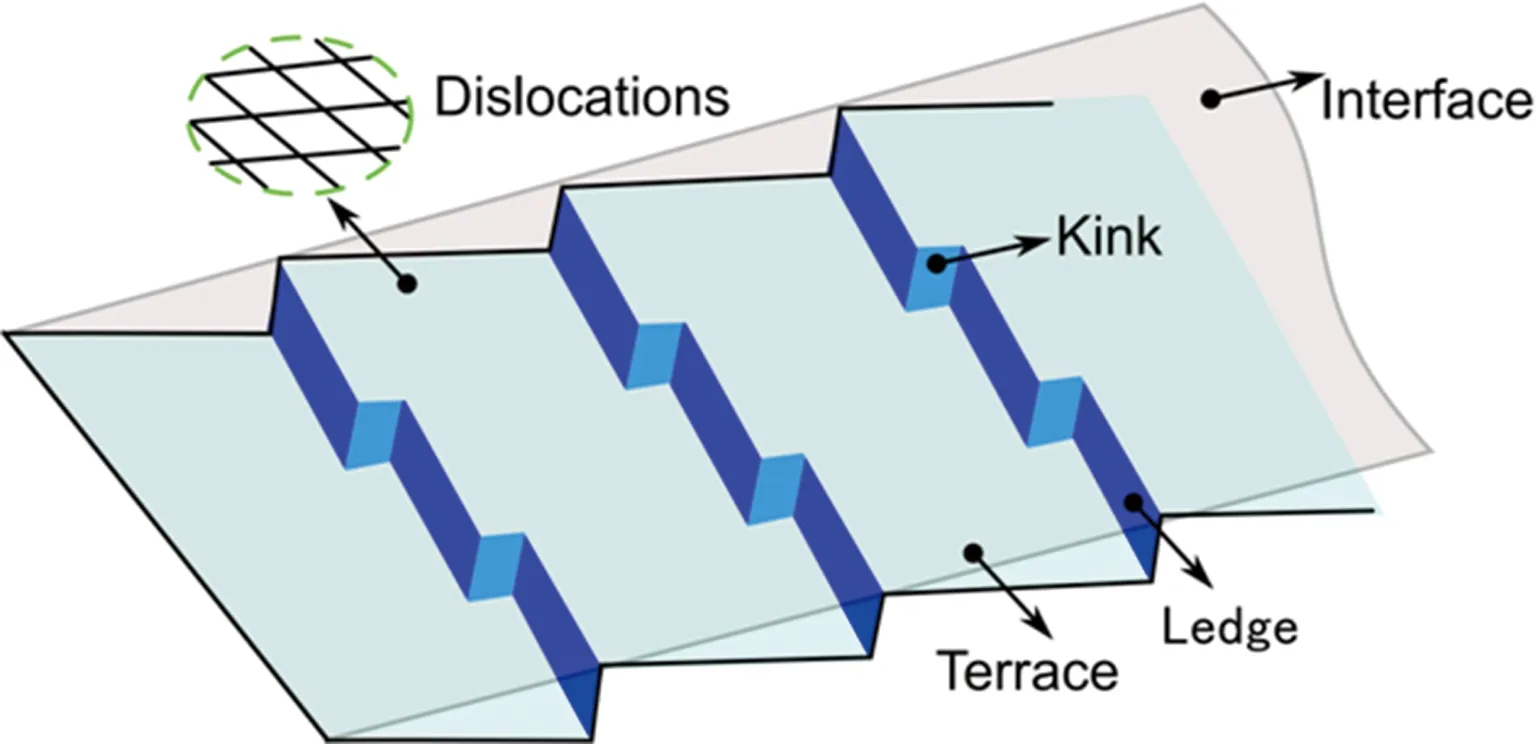
图2 界面的台阶及位错结构Fig.2 The interfacial structures of terrace-ledge-kink (TLK) and dislocations

2 界面匹配

2.1 匹配和错配

相变晶体学几何模型中计算晶格之间匹配的方法是将两个晶格点阵相互穿插并在原点重合，然后计算最近邻的晶格点间的位移大小Δvm，即为错配大小，如图3a所示。异相晶体之间形成完全共格的情况非常少，因此一般界面上两相原子之间都会存在错配。设vα和vβ分别是两相晶格中的晶格矢量，他们间的错配位移为[3]：

(1)

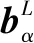
|Δvm|≤δ,

(2)

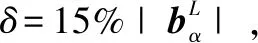
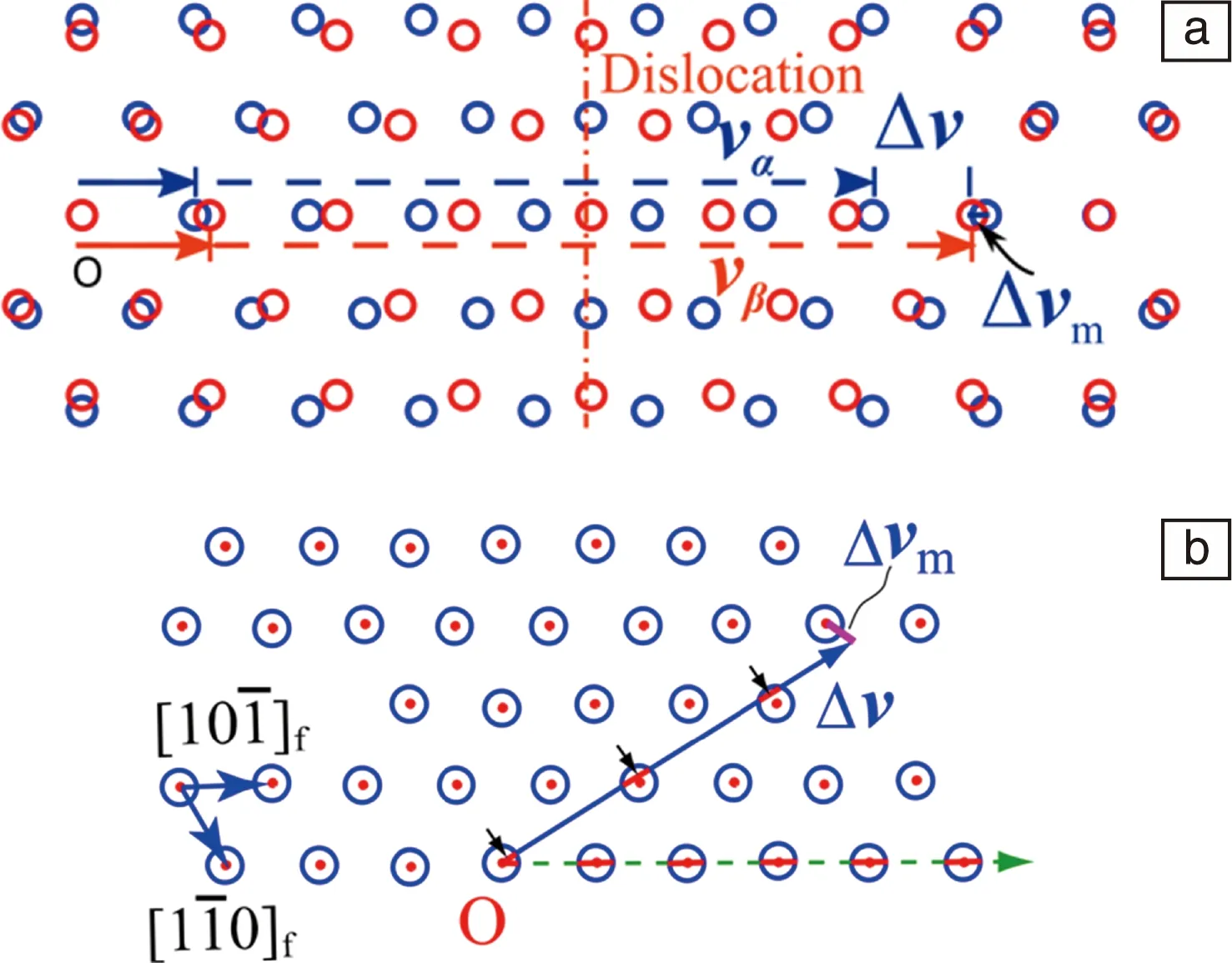
图3 N-W位向关系下((111)f//(011)b,[1-10]f//[100]b)的错配位移(a)，面心立方(111)面内位移矢量Δv=vβ-vα与临界错配圆(球)的交截情况(b)，Δvm为错配位移Fig.3 The misfit displacement at N-W orientation relationship (111)f//(011)b,[1-10]f//[100]b (a); The displacement vector Δv=vβ-vα and matching circle in (111) plane (b), Δvm is the misfit displacement

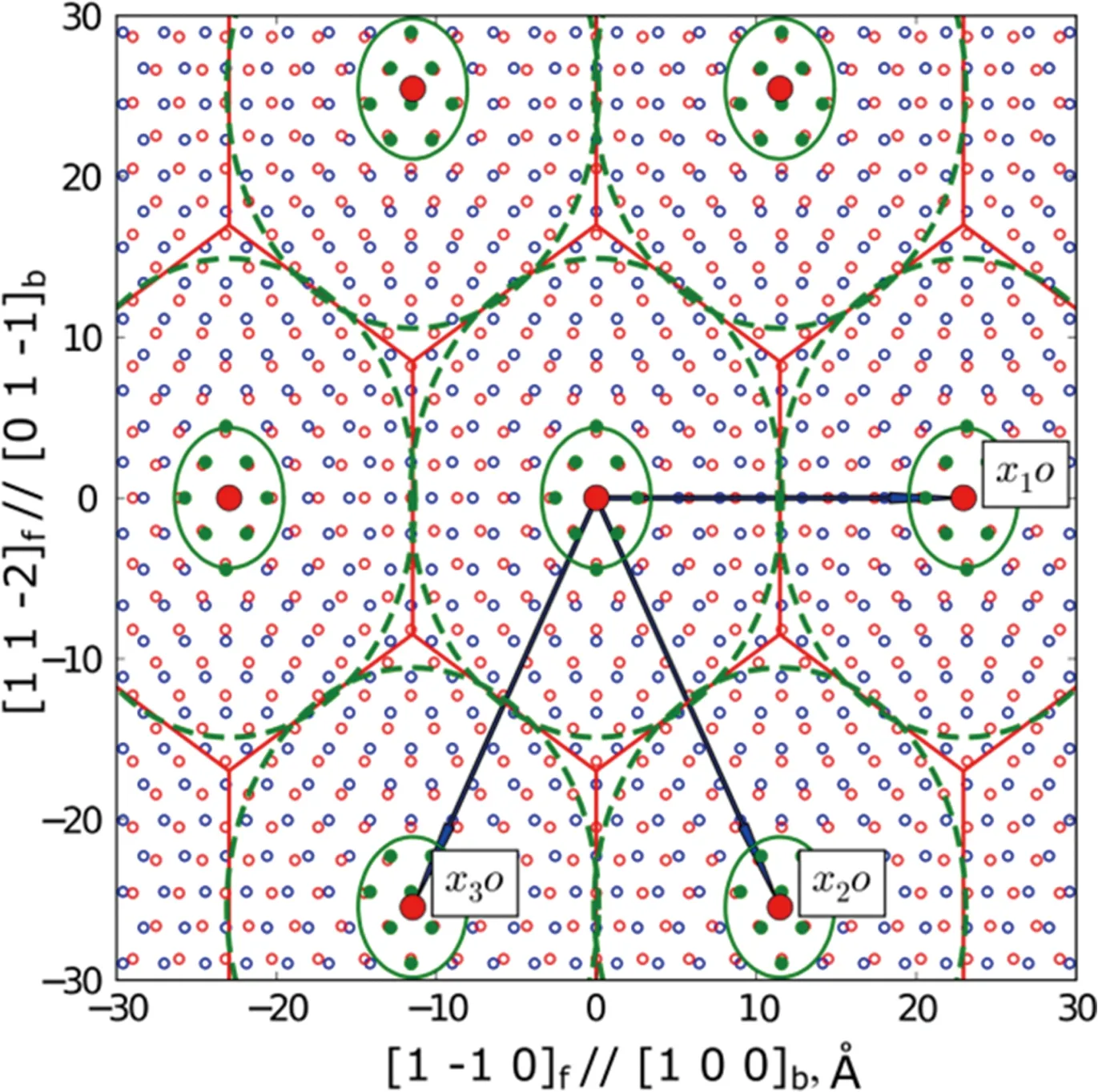
图4 N-W位向关系下，(111)f//(011)b界面的原子匹配，绿色实心圆为匹配好区，实线椭圆为错配时等错配线，虚线椭圆为时等错配线Fig.4 The atomic matching of (111)f//(011)b at N-W orientation relationship, the solid green circles are good matching sites, solid ellipse is the iso-misfit line for misfit of

2.2 界面能与界面匹配

从原子之间相互作用的角度看，原子间相互作用存在着平衡位置，偏离平衡位置会导致系统能量的增加。考虑第一近邻近似，若两相原子在界面处的位置相同或相近，则原子间错配小，那么原子间错配造成的能量增加很少。

在金属材料中，一般界面能中的结构项(错配)占主导(忽略了界面能化学项和熵的贡献)，减小界面的错配度或增加界面原子的匹配度有利于界面能的降低。Chen等[18]通过嵌入原子势函数的方法计算界面能，指出在金属系统中界面能的化学项不超过整个界面能的20%，界面能中的结构项占主导。因此，基于界面错配分析的几何模型适用于界面能结构项占主导的系统。

图5为界面匹配较好的两相界面。实心圆和空心圆分别代表两相的原子，假设两相的原子种类相同。界面处的原子用虚线圆表示，从图中可以看出，界面上两相最相邻的原子近似重合，从第一近邻原则考虑，界面原子的内能与体内的内能相当，也就是界面的能量接近0。GMS法简单直观，但是定量描述界面结构不足，而定量描述界面错配分布的理论是深入理解界面择优规律的基础。

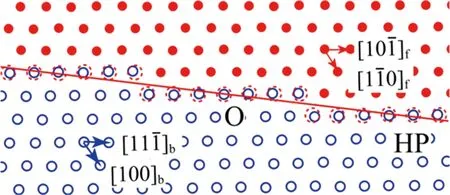
图5 界面匹配与界面能示意图Fig.5 Schematic of the atomic matching at the habit plane and interfacial energy

2.3 O点阵理论

定量描述界面匹配分布及界面结构的数学工具是O点阵理论，由瑞士物理学家Bollmann(1920～2009)提出[19, 20]。O点阵理论定义了匹配好区的中心，即O单元，好区之间的差区的中心称为O胞壁。好区在实际系统中松弛为共格区，差区中心为位错的位置。具体计算方法如下。

设α相和β相晶格中的矢量vα和vβ在公用坐标下通过形变或相变矩阵联系，即：

vβ=Avα

(3a)

其中A为维度3×3的相变矩阵。相应地，倒易空间中两相关矢量gα和gβ之间的相变关系为[2, 20]：

(3b)

正空间矢量vα和vβ之间的位移为：

Δv=vβ-vα=(I-A-1)vβ=Tvβ

(4a)

其中T=I-A-1，被称为相变位移矩阵。与之对应，倒空间中的位移为：

(4b)

根据O点阵理论，O点定义为错配等于0的点，根据式(1)可知：

(5)

那么O点阵的基本平移矢量，即主O点阵矢量xO，定义为[19]：

(6)

O点阵理论中的O单元由主O点阵矢量xO定义，O单元的位置一般不是晶格的格点。方程(6)是否可解与矩阵T的秩相关。

(1)当矩阵T的秩为3时，方程(6)一定可解。主O点阵矢量xO的端点定义O点，任何整数倍的xO矢量仍为O点。3组主O点阵矢量可以定义三维空间中O点阵的周期分布。

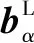
TxIL=0

(7)

通常析出相长轴沿不变线方向[21-23]。若方程(6)可解，在空间分布的周期性O单元为O线，其方向平行于不变线方向。

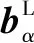
O点事实上定义了匹配好区的中心(错配为0)，若要界面匹配较好，那么界面需要包含两个主O点阵矢量，界面内存在周期性分布的好区，择优界面的单位法向n定义为：

(8)

两个主O点阵矢量构成的平面又被称为主O点阵面。在给定晶体结构和位向关系的情况下，自然选择的择优界面n是固定的，一般平行于主O点阵面。

好区与好区之间必然是匹配差区，其中心为O胞壁，其与界面的截线将是界面位错线所在的位置。O点阵理论给出了计算界面位错位置和间距的方法。界面n上的位错线方向ζ[3, 24]及位错间距D分别为：

(9a)

(9b)

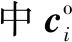
(9c)

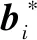
(9d)

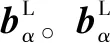
2.4 O点阵与匹配好区分布

GMS一般成团簇分布，团簇的中心为O点。GMS团簇边缘的错配为好区阀值δ。根据式(4a)，原点附近的矢量vβ的位移为Δv，因此原点附近好区团簇内部|Δv|≤δ。因此，GMS好区的边界满足：

vβ′T′Tvβ=δ2

(10)

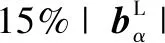
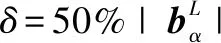
界面匹配好区比例与界面能相关，因此研究界面上的好区分布至关重要。图4为二维(111)f//(011)b面上的GMS团簇分布。面心立方(111)面的堆垛次序是…ABC…堆垛，因此，相邻(111)面之间存在堆垛平移矢量，因此相应的好区也会发生平移。根据两相晶格之间的位向关系，画出相邻三层(111)面上GMS的分布，如图6a所示，不同层的GMS用不同实心符号表示。由于层间的堆垛平移矢量，面上的GMS发生了相对平移。

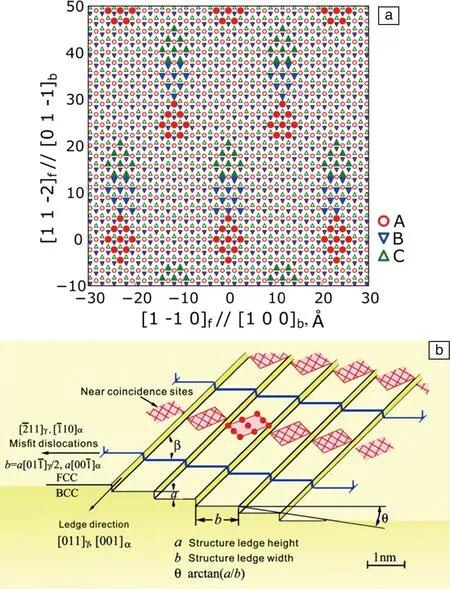
图6 N-W位向关系下，匹配好区在相邻fcc(111)堆垛层上的分布，其中A层原子用圆圈表示，B层用下三角表示，C层原子用上三角表示，匹配好区均用实心符号表示(a)；结构台阶(b)[13, 17]Fig.6 The distribution of GMSs at N-W orientation relationship for neighboring (111) planes with a stacking sequence ABC in fcc lattice. The atoms in each plane are shown by open marks, while GMSs are indicated by solid marks (a); Structural ledge (b)[13, 17]

在相邻层，GMS呈连续分布。若宏观界面偏离(111)面，通过台阶经过层间的GMS，那么就可得到图6b的模型，即经典的结构台阶模型[13, 17]。通过结构台阶，界面上好区呈连续分布，好区之间为界面位错，这种界面的好区比例相对于原始(111)面，由约8%增加到约25%。可想而知，这种界面是晶体学上低能择优的。

由2.1节可知，GMS具体比例在理论上取决于界面上矢量位移和临界错配圆或错配球的关系。根据这些关系也可以类似O点阵对界面择优特征进行分析。对于三维晶格的情况，二维平界面上位移可能沿位移平面内的不同方向，也可能沿同一个方向，也可能位移为0。这3种情况下，界面上匹配好区的比例分别为：

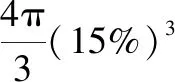
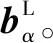
(3)当界面上错配位移均为0时，该界面为共格界面，GMS的比例为100%，界面完全匹配。该界面对应于O点阵中O面的情况。显然界面共格时能量最低。

(4)在一些特殊情况下，界面的位移非连续，只有有限个值，不能采用上述方法估计匹配好区比例。例如界面形成重位点阵，这类界面对应于规则共格界面[5]。这些界面的能量也是较低的。

综上，在上述(1)～(3)的情况下，GMS比例较高的面均为主O点阵面，包含周期性O点阵，即要求界面匹配周期性。然而对于三维晶格的情况，匹配最理想的界面为完全共格界面，如孪晶面。但是两异相晶格之间形成共格界面的情况非常少。因此，足够大的相界面一般会包含缺陷，如位错等，来松弛两相晶格之间的错配。由上面分析可知，含有缺陷的界面最大的好区比例为30%。此时界面包含不变线，且界面位移方向沿柏氏矢量的方向，因而界面上的错配可以通过一组位错松弛。根据O点阵理论，该条件等价于O线条件，即要求惯习面含有O线。由于界面具有较高的GMS比例，因而具有较低的界面能。Zhang和Purdy[24]将界面包含一套O线作为晶体学择优判据，即O线模型，用于计算位向关系和惯习面。与该判据相一致的实验结果是界面上有且仅有一组周期性平行排列的位错。这与他们在Zr-Nb合金中的实验结果相吻合。此后，此择优判据在更多的合金系统中得到了验证，例如双相钢、钛合金等系统[25-28]。

Zhang和Shi[29]提出择优界面具有奇异性的观点，即奇异的界面具有特定的界面结构，位向关系或界面的一点偏离均会造成界面结构的改变而至少增加一套缺陷，从而导致界面能量的增加。这个奇异性可以从位移矢量和匹配球的关系来理解。由于晶体结构是分立的，位移方向只有沿低指数方向才能使得GMS比例最高，而任何方向偏离均会造成GMS比例降低，即匹配好区周期性丧失。且从位移角度考虑还可以帮助理解为什么会增加至少一套缺陷，如当位移沿柏氏矢量时，仅需一组位错来补偿错配，而当位移偏离柏氏矢量时，需要额外柏氏矢量来补偿错配的位移，即增加了位错的数目。因此，当界面包含一组位错时，任何位向关系或界面取向的改变均会造成该界面结构的改变，因此含O线的界面是局部低能的。关于奇异界面种类可参见文献[3, 30]。

2.5 O点阵与倒空间矢量Δg

在给定位向关系下，主O点阵面是择优界面。位向关系、界面取向等通常通过透射电子显微镜(TEM)的衍射方法确定。实验获得的衍射花样直接对应倒空间矢量(g)，因此，理解倒空间矢量与界面的法向之间的关系，将为表征界面结构打开方便之门。

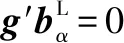
(11)

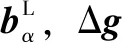
(12)

因此，根据式(11)和式(12)可知，Δg也垂直于O线所在的面。总之，不论T的秩如何，若O点阵方程(6)可解，择优界面一定垂直于一个Δg矢量。这一择优关系可在TEM中对比界面迹线及衍射斑确定。在正空间中，Δg垂直于水纹面(Moiré面)，相关的两个g面在Moiré面两侧一一匹配，如图7所示。就是说，择优界面两侧至少有一组晶面在界面上边边匹配。由于Δg矢量不一定是低指数方向，这也解释了高指数界面(无理界面)择优的原因。

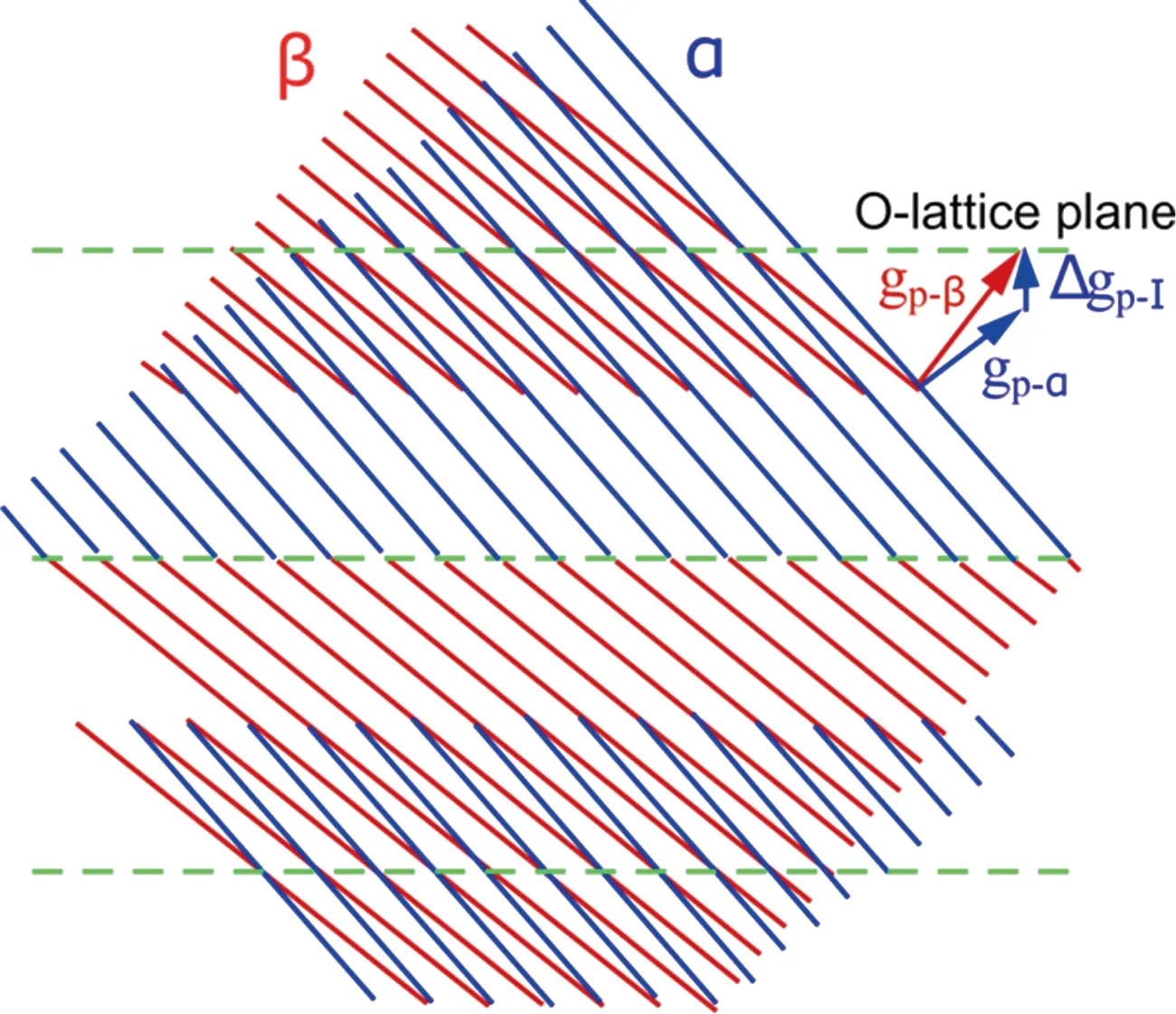
图7 Moiré面及面与面之间在界面处的匹配[3]Fig.7 Moiré plane and plane to plane matching at the interface[3]

2.6 几种相变相关矩阵的关系

在实际相变晶体学分析过程中，往往涉及矢量在晶体坐标系、公用坐标系之间的变换，以及联系不同坐标系内矢量的矩阵。这些转换和矩阵初学者在实际应用时最容易混淆，值得多加注意。

图8总结了几种坐标系和矩阵之间的关系。矩阵S为结构矩阵，其将矢量由晶体坐标系转换到晶体坐标系相关的直角坐标系，以方便计算[32]。母相和新相各有一个S矩阵，通常将母相的直角坐标系作为公用坐标系，计算相变矩阵A等。位向关系矩阵M是同一矢量在两相晶格直角坐标系之间的转换矩阵。晶格对应关系C为相变矩阵A相关联的两个晶体坐标系下的矢量。这几个矩阵之间的关系如式(13)：

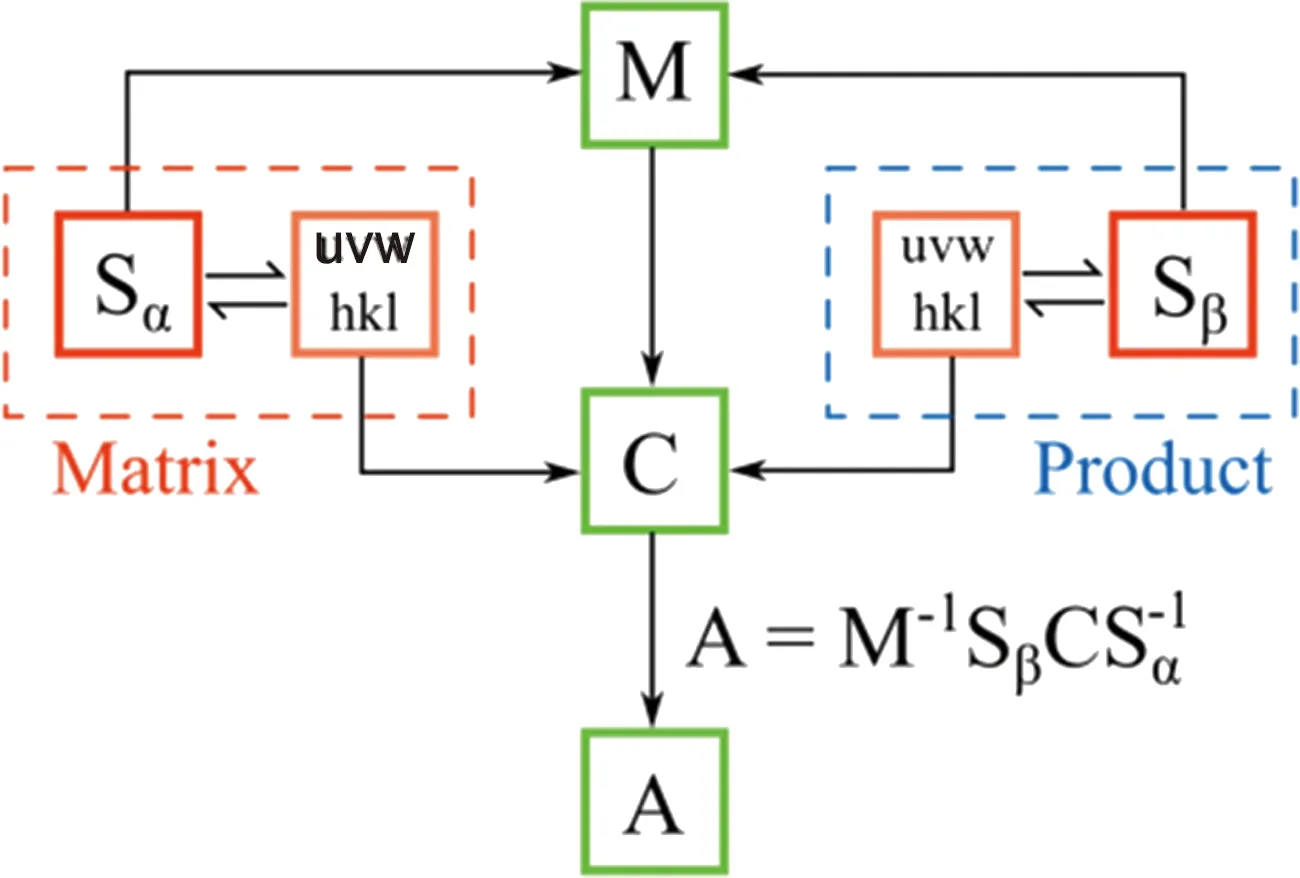
图8 母相(α)和新相(β)的结构矩阵S、两相之间的位向关系矩阵M、晶格对应关系矩阵C及相变矩阵A之间的关系Fig.8 Relationship between structure matrix S in matrix (α) and product phase (β), orientation matrix M, lattice correspondence C and phase transformation matrix A

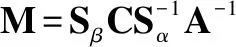
(13)

相变矩阵与位向关系矩阵、晶格对应关系及结构矩阵相关。如果知道两晶格结构及位向关系矩阵，可通过原点附近GMS团簇寻找晶格对应关系并构造相变矩阵[4]。由于晶体自身的对称性，晶体可以有多种晶体坐标系选择，因而导致同一原子位置可以有多种描述，位向关系矩阵表达就不同。一般在计算过程中，选择取向差最小对应的位向关系。

3 相变晶体学预测模型

前面介绍的方法是在已知位向关系的前提下，如何确定择优界面。而预测两相的位向关系和择优界面能够在很多情况下预测析出相的形貌，对材料设计非常有价值。这可基于界面择优的性质实现，下面简单介绍一些常用的相变晶体学预测模型。

3.1 直接法

通常，位向关系偏向用密排面或密排方向之间的平行关系来表示。将两相中所有低指数的方向或面进行比对，如果某一对方向和方向所在的面错配小于给定的阀值(例如15%)，则认为这一位向关系可能择优。最终计算结果可能有多种解，错配最小的解是最可能被实验观察到的位向关系。界面至少包含两个低错配方向。最近，Zhang等[33]提出了原子列匹配模型预测位向关系。该模型第一步是寻找一个错配较小的低指数方向，第二步是寻找错配沿第一步方向投影较小的低指数方向，以实现界面近似原子列匹配。以该模型为代表的这类方法简单，但是不能解释某些偏离有理位向的位向关系(无理位向关系)，需结合其它模型(例如后文的Δg平行法则)优化。

3.2 马氏体表象理论

马氏体表象理论[34]是相变晶体学研究中里程碑式的工作，是相变晶体学成功应用的典范，并对后来扩散型相变晶体学的发展起到促进作用。马氏体表象理论可以预测马氏体的晶体学特征，包括位向关系、惯习面、孪晶分数等。表象理论的提出是基于一些实验基础或假设：① 惯习面是宏观不变平面；② 界面可滑动。宏观不变平面应变P1可写成晶格间变形的均匀应变和非均匀应变(点阵不变切变)之积，如式(14)：

P1=RBP2

(14)

其中B为由面心立方转变为体心立方的贝茵应变(均匀应变)，P2为点阵不变切变(非均匀应变)，如滑移或孪晶，R为旋转矩阵，使得界面旋回原始位置形成宏观不变平面。根据式(14)可得，表象理论中有两条重要的性质：① 界面包含一根不变线，不变线位于滑移面或孪晶面上，位错线或孪晶在界面的迹线平行于不变线；② 界面的错配位移沿着点阵不变切变的方向。根据这两条性质可以运用解析法求解马氏体的晶体学。

3.3 O线模型

由2.4节可知，若系统能满足O线条件，即界面通过一组位错松弛，界面GMS比例可高达30%。Zhang等[24]直接以界面存在O线作为判据，从而预测可能的位向关系，称为O线模型。该模型成功用于双相钢、钛合金等系统[25-28]。

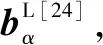
(15)

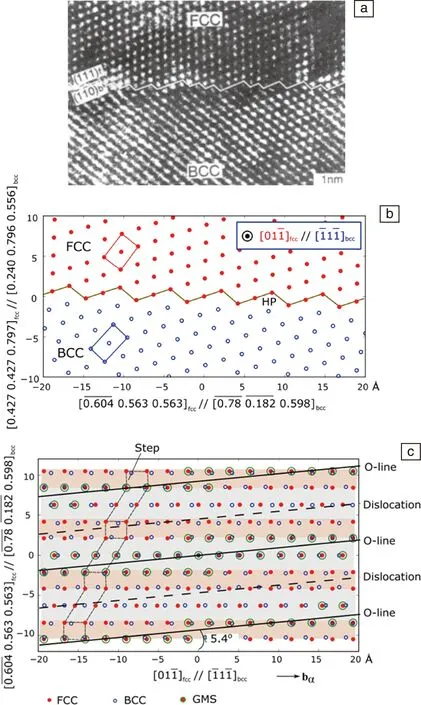
图9 Ni-Cr合金系统中，界面高分辨照片(a)[36]，相应的界面原子匹配图(b)[4]，界面内原子匹配图(c)[4]Fig.9 High-resolution TEM image of the habit plane in Ni-Cr alloy (a) [36], simulated atomic matching across the interface (b)[4], the atomic matching in the interface (c)[4]

3.4 Δg平行法则

根据O点阵理论，择优界面平行于主O点阵面，即至少垂直于一个Δg。考察Δg与其它倒易矢量之间的关系，Zhang等[9]总结出了Δg平行法则：

法则Ⅰ：Δg//g

法则Ⅱ：Δg1//Δg2

法则Ⅲ：ΔgII//Δg

法则 Ⅰ 适用于陶瓷系统，一侧界面垂直于低指数g；法则Ⅱ即为O线模型，适用于小错配系统；法则Ⅲ适用大错配系统，要求二次位错的周期与台阶重合[11]。择优位向关系至少满足3条法则之一。满足这些法则的合金系统参见文献[3]。在倒空间观察位向关系、惯习面取向及Δg是比较方便的。因为Δg平行法则与界面可能的择优结构相对应，可对相变中界面的结构进行解释，运用该法则不但可以帮助我们理解界面的择优规律，还可帮助我们在倒空间寻找两相晶格对应关系，从而建立相变应变。

3.5 边边匹配模型

界面上原子列匹配是一种低能的结构。Kelly和Zhang在此基础上提出了边边匹配模型(edge-to-edge matching model)[38]。基本思路如下：① 选择两相中一组平行的低指数晶向，两者错配之差小于10%(经验值)；② 包含这个晶向的晶面之间的间距接近(<6%)；③ 绕平行的晶向旋转，步骤②中的晶面的原子列在界面上边边匹配。由于晶面在界面边边匹配，界面也垂直于Δg。边边匹配模型简单，但是只有在特殊的晶格常数下才能实现第三步，后来，Kelly和Zhang借助于Δg平行取代第三步[6]。

4 相变晶体学计算软件

为了便于运用上述模型求解相变晶体学特征，作者团队[32]基于Python编程语言开发了免费的相变晶体学计算软件PTCLab(https://sourceforge.net/projects/tclab/)。该软件支持常见的相变晶体学模型(包括马氏体相变晶体学，扩散型相变的相变晶体学)、衍射斑模拟与标定和极射投影图绘制，软件支持主流操作系统。软件的操作界面如图10a所示，主要由菜单①、工具栏②、树形菜单③及显示界面④组成。软件的3大主要功能及其子功能见图10b，这些功能的计算仅需输入晶体结构。

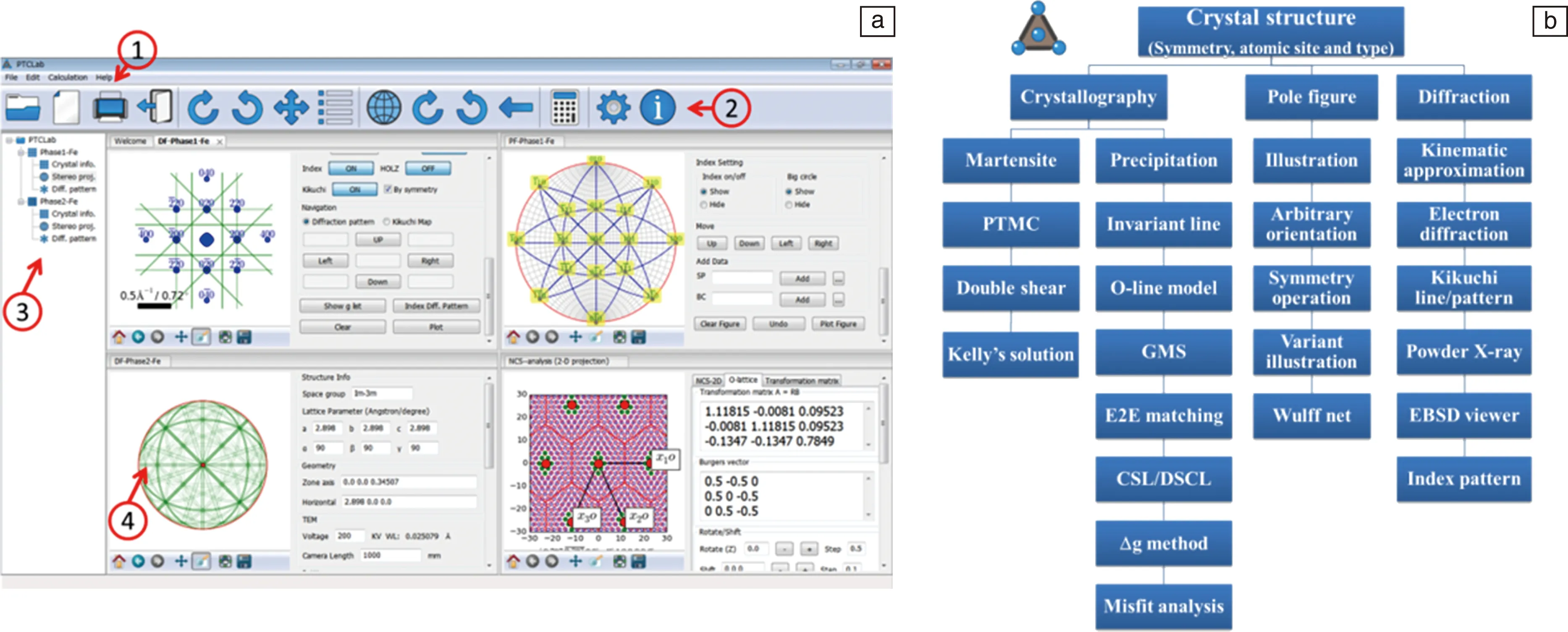
图10 PTCLab主界面及功能[32]：(a)主界面，(b)主要功能Fig.10 The main interface (a) and main functions (b) of free software PTCLab[32]

5 相变晶体学应用

由于篇幅限制，这里仅介绍运用PTCLab软件中的O线模型模块解释双相不锈钢系统中δ铁素体(bcc)母相与析出相γ奥氏体(fcc)之间的相变晶体学特征。

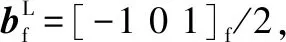
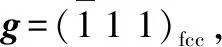
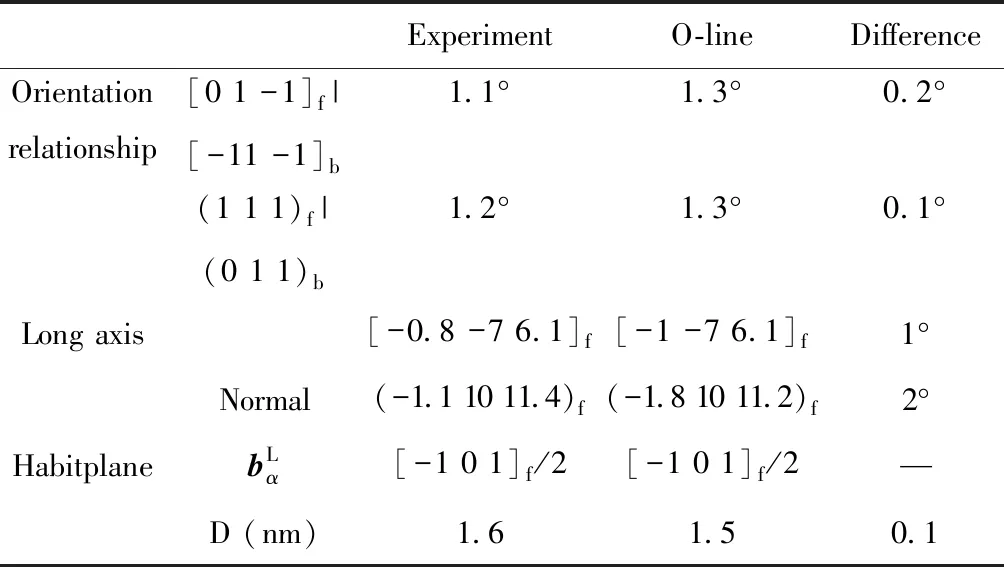
表1 一种双相不锈钢中奥氏体析出相的相变晶体学试验结果与O线模型结果的比较

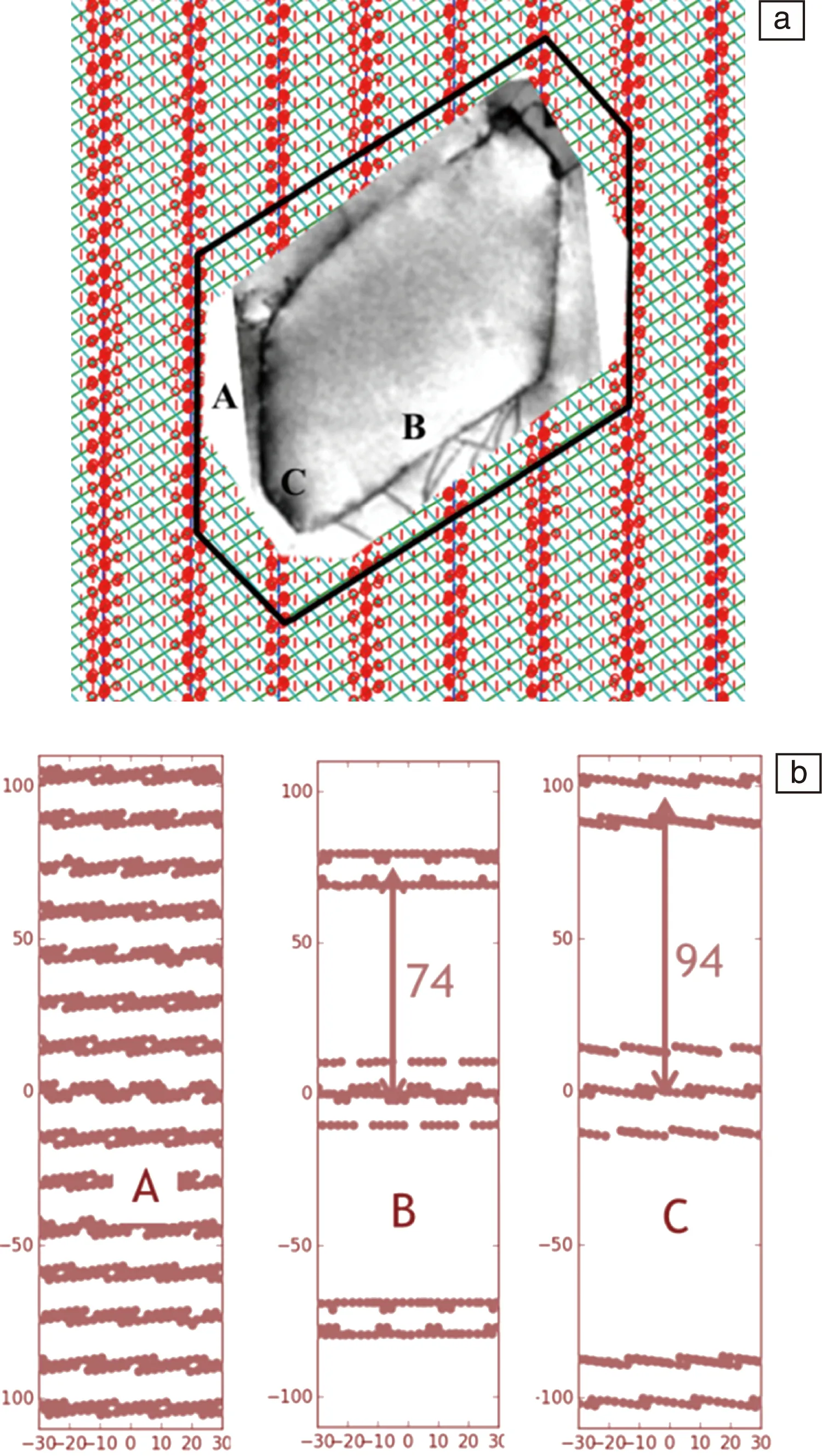
图11 一种双相不锈钢中奥氏体析出相的相变晶体学计算结果：(a)三维好区(GMS，红点)沿长轴方向的投影分布及实际析出相的形貌[16]；(b)析出相各界面A、B、C上好区GMS分布,水平方向为不变线方向(长轴方向)，图中长度单位为埃Fig.11 The calculated transformation crystallography for the austenite precipitates in a duplex stainless steel: (a) The distribution of the GMS (red dots) along the growth direction and the morphology of a precipitate[16]; (b) the distribution of GMS in A, B, C interfaces, and the horizontal axis is along the growth direction, the unit in the figure is angstrom

6 结 语

本文介绍了理解相变晶体学择优规律的错配分析法。界面匹配是分析相变晶体学择优的关键。择优界面一般具有较高的匹配好区比例，垂直于倒空间矢量差Δg。特别地，界面若满足某些特定的择优结构，例如界面包含一套位错，位向关系往往具有特定的限制条件。界面结构可通过好区分布或O点阵理论进行定量计算。由于计算机技术的发展，相比过去，相变晶体学模型已经变得更容易学习和应用。相变晶体学模型通常以晶格常数为简单输入，可以输出丰富的相变晶体学数据。常见的相变晶体学模型已经集成于作者研究组开发的免费软件PTCLab中。基于对相变晶体学特征的理解，人们有望在今后更好地理解相界面结构与力学性能的关系、界面性质与界面溶质原子偏聚之间的关系[39-41]、析出相与缺陷的相互作用关系[42, 43]等。

致谢:感谢清华大学张文征教授及日本东北大学金属材料研究所FURUHARA Tadashi教授一直以来对作者在相变晶体学及界面研究方面的帮助和指导。