新课标下多角度探究三角形面积的最值问题
孙 娇 阳
(无锡市堰桥高级中学,江苏 无锡 214171)
2017年版新课标,重点指出教师在教学和考试中,不仅要重视对数学三个基本(基本知识、基本技能、基本思想方法)的考查,要重视对数学两种能力(基本能力和综合能力)的考查,更要注重对数学两种意识(应用意识和创新意识)的考查。在解三角形面积的最值问题的求解过程中,不仅需要学生能够灵活的运用正余弦定理和三角形面积公式等解三角形的基本知识方法,更需要他们能够结合平面几何、基本不等式以及函数的最值等相关知识来解决问题。所以此类问题能够较好地体现新课标要求,考查学生基本知识、技能、思想方法,并且能够提高学生的知识迁移能力和综合应用能力。
解三角形章节中面积的最值问题,条件灵活多变,本文主要着眼于条件是以边的二次关系呈现,并且具有对称性这一类题型的探究。解决此类问题需要学会抓住条件特点,从多角度进行分析求解,达到新课标对数学综合能力的要求。
一、真题呈现与简析
例题:在ΔABC中,角A,B,C的对边分别为a,b,c,若∠B=∠C且

本题是2015年江苏省泰州市第二次模拟考试填空第13题,是典型的三角形面积最值的求解问题。主要考查在三角形中正、余弦定理的运用,进行边角关系的互相转化。通过建立所求三角形面积的函数模型,然后利用求解函数最值问题的多种方法求解三角形面积的最大值。在求解过程中还考查学生的运算求解、逻辑推理能力,考查数形结合、转化与化归等数学思想方法。试题表述简洁,内涵却很丰富,对学生能力要求很高,难度较大,值得钻研探究。根据学生的解题情况反馈,发现大多数学生能够运用正、余弦定理进行转化,但转化方向不够明确,导致多数学生半途而废,不能成功做出最后结果。下面,笔者从不同角度对此题进行分析求解,供学生学习时参考借鉴。
二、探究思路及解法
探究目标1:突出三个基本
思路1:角化边。求三角形面积的最值,可以利用余弦定理和同角三角函数关系,将三角形面积公式中的两边一角都转化为某一条边的函数,转化成初等函数求解最值问题。



思路2:边化角。求三角形面积的最值,可以利用余弦定理和本题中边的对称关系,将三角形面积中的边转化为面积中同一个角的三角函数,利用导数工具求解最值。

接下来利用导数求面积的最大值.

当A∈(0,A0)时,S'>0;当A∈(A0,π)时,S'<0.

评注:探究目标1中的两种解法,都是利用解三角形中的知识进行边角互化,将面积的最值转化为关于一条边或者一个角的函数,最终利用二次函数和导数来求解最值问题。解法1利用二次函数求解最值,考查了学生运用初等函数这一基本知识的能力;解法2利用导数工具求解最值,考查了学生利用导数工具求解最值这一基本技能;在两种解法的解题过程中,转化与划归这一基本思想方法贯穿始终。这样的思路和求解方法,有助于强化学生数学的基本知识、基本技能、基本思想方法。
探究目标2:重视两种能力
思路3:运用基本不等式。观察发现余弦定理和面积公式的结构中,可以利用同角三角函数平方关系消去角,结合基本不等式,把问题转化为三角形面积和一条边的不等关系,最后利用二次函数求解最值。
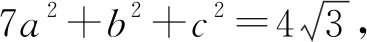

即16S2当且仅当时
评注:探究目标2中的解法是先将解三角形中面积公式与余弦定理公式相结合,通过同角三角函数平方关系消去角,这里考查了学生数据处理和运算求解的基本能力;由于消去角后得到的等式中有两边的乘积,想到与基本不等式知识相结合,转化为两边的平方关系,再结合条件中的等式将三边转化为只有一条边和面积的不等关系,再利用二次函数求解最值,充分的体现了运用有关知识和方法分析和解决问题的综合能力。 这样的思路与求解方法,有助于学生基本能力和综合能力的培养。
探究目标3:注重两种意识


解法4:以BC所在直线为x轴,BC的中垂线为y轴,如图建立平面直角坐标系,


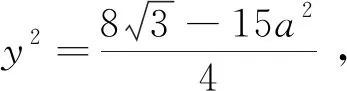


思路5:代数问题几何化。前半部分面积的转化同思路2,转化为一个角的函数;后半部分求最值,没有从函数导数的视角出发,而是另辟蹊径,把目标函数看成两点连线的斜率,而其中的一个点P(cosA,sinA),它的轨迹就是单位圆,面积取得最值转化为直线斜率取得最值,即为直线与圆相切时,求解变得更加简单.



由A∈(0,π)知:点P的轨迹是x轴上方的半圆,f(A)取最小值时,PQ与半圆相切;


评注:探究目标3的两种解法都是将解三角形问题与平面解析几何相结合,灵活的转换视角,解法4凭借几何问题代数化的观点,利用建系法,将三角形中的边角关系,转化为坐标来进行求解;解法5凭借代数问题几何化的观点,将三角形面积的最值问题转化到解析几何中直线与圆相切这一特殊状态,充分利用了数形结合的思想,使问题求解更趋于简单。这样的求解思路和方法,有助于学生数学的应用意识和创新意识的提高。
三、一点思考和感悟
本文选取解三角形面积的最值问题中比较有代表性的一个例题,用五种解题思路和方法对题目进行分析求解。从整个的分析和求解过程看,例题不仅涉及到了解三角形中正余弦定理、面积公式、三角函数平方关系式,还包括了基本不等式、函数、解析几何等知识的运用。不仅体现了各种数学知识之间的内在联系,也体现了构造法、消元法、配方法、解析法以及数形结合、转化与化归等数学方法、思想的运用与渗透。看似简单的一道模拟试题,如果教师能够充分的汲取在分析和求解中用到的数学方法和数学思想,它的作用和价值就会得到更多的体现。学会用这些方法解题,对于同学发散思维的培养、灵活解题能力的加强、数学素养的提高也会起到非常大的作用。
新课标理念下的高考,突出对学生数学综合能力的考查,这样就更能体现研究一题多解的意义。本文通过五种角度对例题进行研究,不仅达到了新课标提出的教师对于学生各种数学能力和意识培养的要求,而且还发现一题多解能让一个优秀的数学试题发挥其最大的价值.在高三繁重的数学复习中,题海战术似乎已经成为了一种最常用的模式.但是这种模式是不是最有效的呢?还是因为能力达不到才采用的一种由量变产生质变的方法.通过一道题多角度的分析,我们不仅将题目中涉及到的基础知识和方法进行了巩固与强化,还将许多其他章节的知识点与本题知识点进行结合与转化,形成一整套的知识体系,最终帮助学生实现多题一解,触类旁通,化繁为简。

