Ti, Nb, Al及其二元合金状态方程的第一原理计算及其应用

程 超， 马云莉， 曹超铭， 孙嘉兴， 刘艳侠

(辽宁大学物理学院，沈阳 110036)

1 引 言

如果金属状态方程可被求解，那么金属的许多能量机制就可以被了解，金属状态方程可用于求解金属性质的诸多领域，其中一个重要应用用于拟合或验证原子间相互作用势. 原子间相互作用势是有关原子尺度计算机模拟的基础，它的精确与否将直接的影响到模拟的准确性. 如此重要的同时，原子间相互作用势的构建也是方法众多，并且涵盖材料物理性质也不尽相同. 但如此众多的不同中存在着相同之处，就是都要满足体系能量随原子间距离的变化关系 (E-r关系).

然而，金属状态方程一直以来是难以确定的，直到1984年，Rose等人[1]针对金属状态方程进行研究，并提出了金属状态方程的普适形式. 时至今日，Rose的状态方程在原子间相互作用势等计算物理领域有重要的应用. 本文将Rose状态方程可视化，画出E-r曲线作为参考，对比第一原理计算结果，探究计算E-r曲线计算的最优方法. 之所以采用第一原理计算是由于，早年研究[2-5]表明，在拟合原子间相互作用势时， 如果结合第一原理数据可以显著提高势函数的精确性. 例如，Baskes等人[4]通过拟合势函数和第一原理研究了Al原子间相互作用力的范围. 他们发现，在拟合过程中，使用第一原理数据拟合的势比使用实验数据拟合更准确. 但使用第一原理探究金属及其合金E-r关系却鲜有报道.

本文通过使用基于密度泛函理论的VASP软件包进行第一原理计算[6, 7]，计算并探究了航空航天常用材料Ti及合金化元素Nb和Al在使用不同赝势计算E-r曲线的差异性，研究了由三种金属分别构成的二元合金β相的Ti-25Nb(at.%)合金， L10结构的TiAl合金以及DO22结构的NbAl3合金的第一原理计算精确度. 并且我们以Ti-Nb系合金为例，分析了合金成分不同时，其E-r关系满足的一般规律. 根据材料的E-r关系，使用最小二乘法拟合了材料的体弹性模量. 根据合金曲线表现出的规律，提出合金E-r关系的新的计算方法，并且发现使用该方法得到的合金的E-r关系数据拟合体弹性模量的精确度非常高. 本文工作旨在为原子间相互作用势的构建及验证提供理论数据支持.

2 计算方法和模型

2.1 计算方法

本文第一原理计算采用基于密度泛函理论[8](DFT)的VASP软件包[9, 10](Vienna Ab initio Simulation Package)进行的. 选择广义梯度近似GGA[11, 12](Generalized gradient approximation)以及局域密度近似LDA[13, 14](Local-density approximation)来处理电子的交换关联能. 自洽精度取1×10-5eV/atom，通过采用Monkhorst-Pack方法[15]选取布里渊区k空间网格点来进行体系总能量的布里渊区积分计算，且计算考虑了自旋极化. 自洽迭代循环中，总能的收敛标准选取 1×10-4， 原子弛豫收敛标准取 0.01，原子弛豫最大步数设置为 100，并采用共轭梯度算法来优化原子的位置. 对于2×2×2超胞的Ti-Nb合金，K-points 取 6×6×6，对于1×2×1超胞的TiAl合金以及NbAl3合金K-points 取 6×4×6.

对所选体系进行结构优化，再取结构优化后的模型，缩放其晶胞尺寸计算能量. 对于作为对比分析的Rose曲线而言，我们根据Rose的普适性状态方程，并用数学计算软件Mathematica计算数据，计算选取的对应金属实验值在本文表2中列出.

2.2 计算模型

如图1所示，本文计算模型结构均为常温下稳定结构. 纯金属为单胞的HCP-Ti，BCC-Nb和FCC-Al，合金为2×2×2超胞的β相Ti-25Nb(at.%)合金，1×2×1超胞L10结构的TiAl合金以及1×2×1超胞DO22结构的NbAl3合金. 图1给出的模型结构(010)面向上，右侧为(100)面.

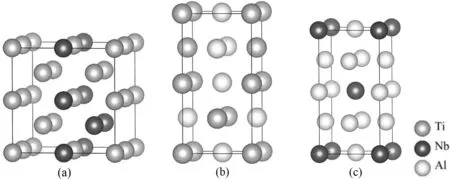
图1 合金结构 (a) Ti-25Nb(at.%); (b) TiAl; (c) NbAl3Fig.1 Structures of alloy (a) Ti-25Nb (at.%), (b) TiAl, (c) NbAl3

3 结果与讨论

3.1 Ti,Nb和Al的能量以及 E-r曲线分析

体系结合能计算公式为：

(1)

公式中Etot为体系总能量，E1与E2为体系中不同元素的孤立原子能量，n和m为对应元素的原子个数. 表1为Ti,Nb和Al使用不同赝势计算出的结合能并与实验值进行对比. 如表1所示，三种金属计算结果表明，选用GGA方法处理的结果明显优于LDA方法，而相比较之下同样是广义梯度近似，使用GGA-PBE[16]赝势计算金属Ti和Al的结果比GGA-PW91[17]赝势的计算结果更加的接近实验值. 而对于金属Nb而言，使用GGA-PW91赝势计算的结果与实验值更接近.

表1 不同赝势计算的结合能

Table 1 The results of cohesive energy calculated by different pseudopotentials

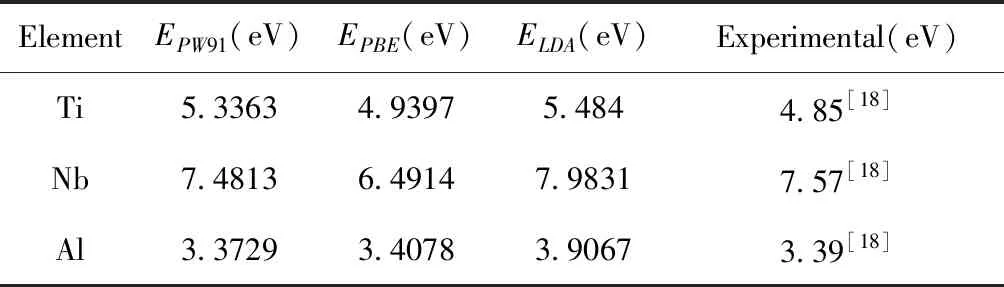
ElementEPW91(eV)EPBE(eV)ELDA(eV)Experimental(eV)Ti5.33634.93975.4844.85[18]Nb7.48136.49147.98317.57[18]Al3.37293.40783.90673.39[18]

金属的状态方程对于了解金属能量学等方面至关重要. Rose就金属的状态方程做过研究并且给出了普适的状态方程，忽略高次项为：

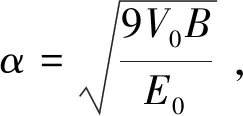
表2 Rose曲线计算所用数据

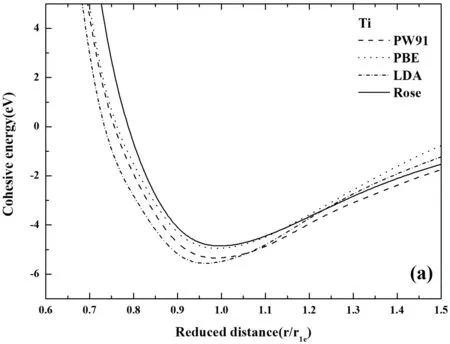
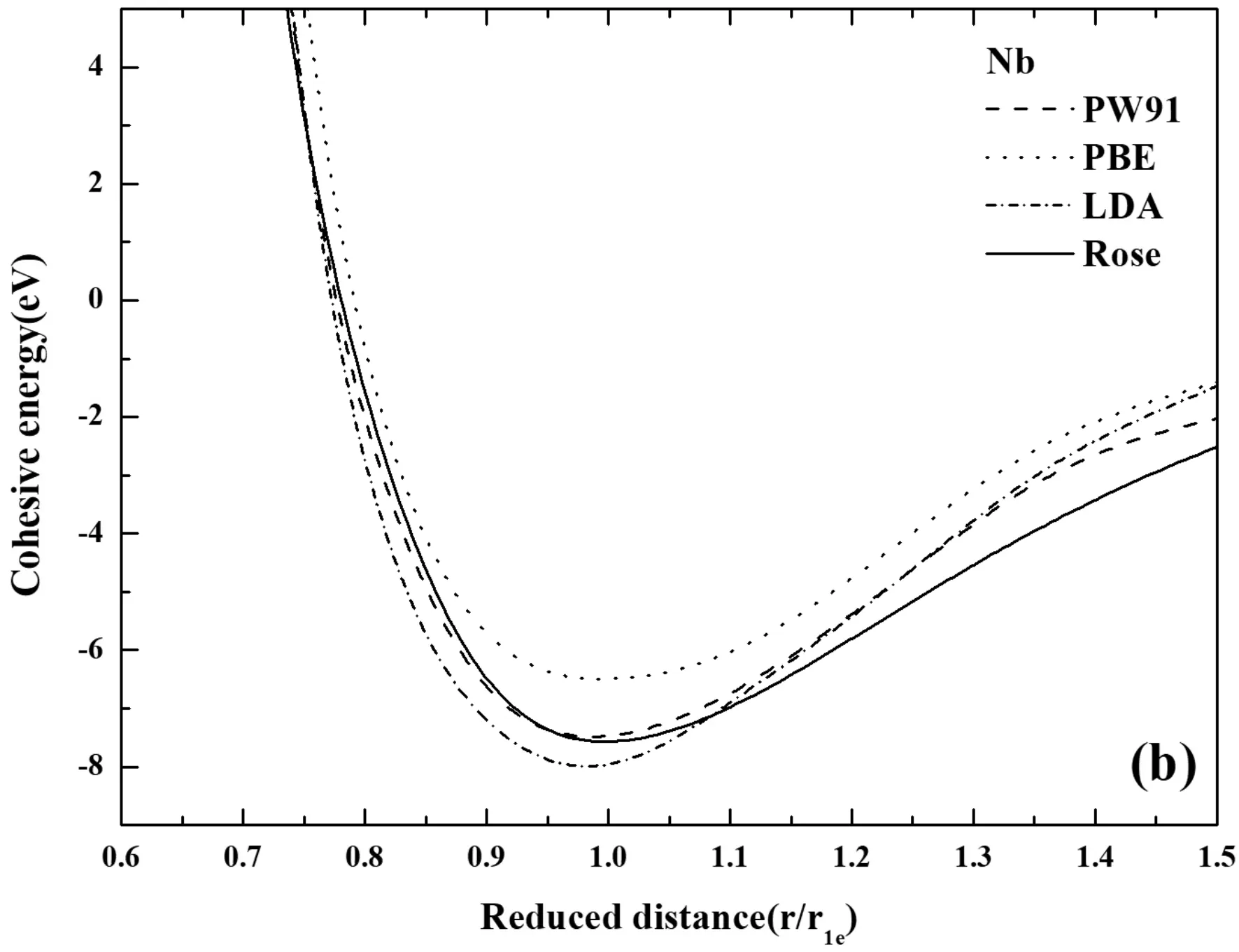
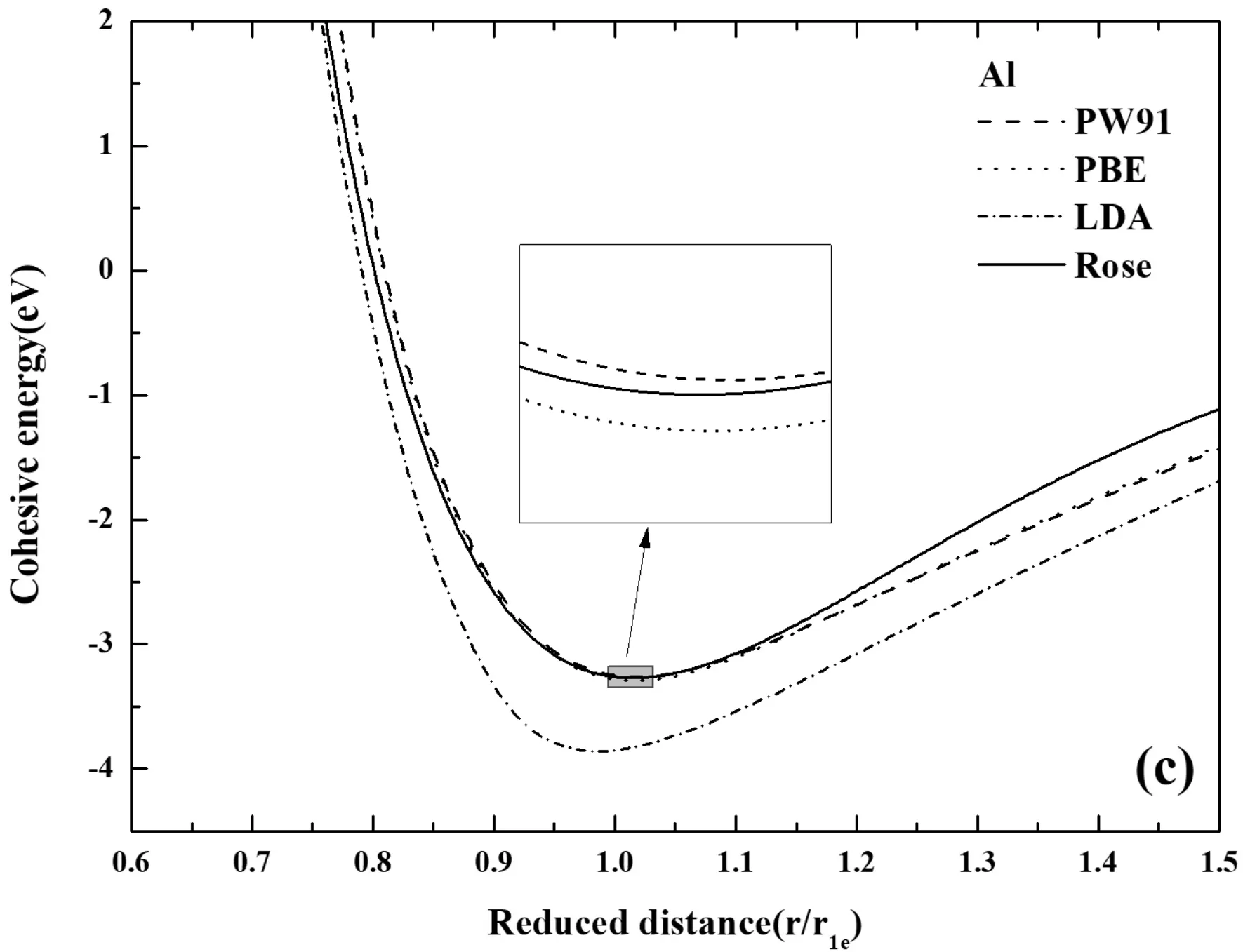
图2 不同方法计算的E-r曲线(a) Ti, (b) Nb, (c) Al Fig.2 The comparison of E-r curves calculated by different methods (a) Ti, (b) Nb, (c) Al

如图2所示，第一原理计算和Rose状态方程所得到的E-r关系对比分析，发现，第一原理使用不同赝势计算得出的曲线大体上近似，却有着不可忽视的差别. 所有的探究都表现出，平衡态右侧部分的第一原理计算结果与Rose曲线稍有偏差，而平衡态左侧部分，金属Al和Nb的第一原理计算结果与Rose曲线吻合得很好，但金属Ti却相差较大. 如图2(a)中，对比发现无论在高能量的排斥区还是低能量的吸引区域，GGA-PBE赝势都要比另外两种方法计算的结果更加的接近Rose曲线，并且发现在平衡态处计算的能量与Rose曲线最接近. 这都展现出，对于金属Ti而言PBE赝势计算的更加准确. 在图2(b)中，GGA-PW91赝势的计算结果更接近于Rose曲线，同时结合表1的计算结果也表明，采用GGA-PW91赝势计算Nb更为精确. 如图2(c)，可以看出，第一原理计算的结果与Rose曲线吻合度很高，而且PW91计算结果与PBE计算结果几乎重合，如图2(c),可以看到PW91赝势计算结果与PBE赝势计算结果的细小差别，难以分辨哪个结果与Rose更接近，但是从结合能计算的结果来看，如表1所示，使用PW91赝势计算结合能为3.3729 eV，而PBE赝势为3.4078 eV，相比较而言，PBE赝势计算结果更加的精确.

3.2 合金体系的E-r曲线分析

如图3，分别为β相Ti-25Nb(at.%)合金，L10结构TiAl合金以及DO22结构NbAl3合金E-r关系的第一原理计算结果. 对于每种合金的合金化元素我们都选取上述工作中最优的计算结果，比如，金属Ti和Al选用GGA-PBE的计算结果，而金属Nb则选用GGA-PW91计算结果. 从图3可以看到，合金的E-r曲线分布处于其合金化元素E-r曲线之间，这与已有的研究结果一致[23]，可见计算结果吻合度不错.

为了探究和合金化元素成分不同对合金E-r曲线的影响，我们又选取了Ti-37.5Nb(at.%)合金[24]以及Ti-50Nb(at.%)合金[21]进行了对比计算，如图3(e)所示. 可以看到，合金的成分虽然改变但曲线仍然处在其合金化元素曲线之间，且随着Nb元素含量的提高，合金曲线越趋近于Nb的曲线，Nb含量较少的Ti-25Nb(at.%)合金曲线更接近于Ti的曲线. 这也就表明同种合金系合金的E-r关系，处于其合金化元素之间，不会超出或低于该范围；并且合金的曲线会更靠近合金内含量较高的元素的E-r曲线.

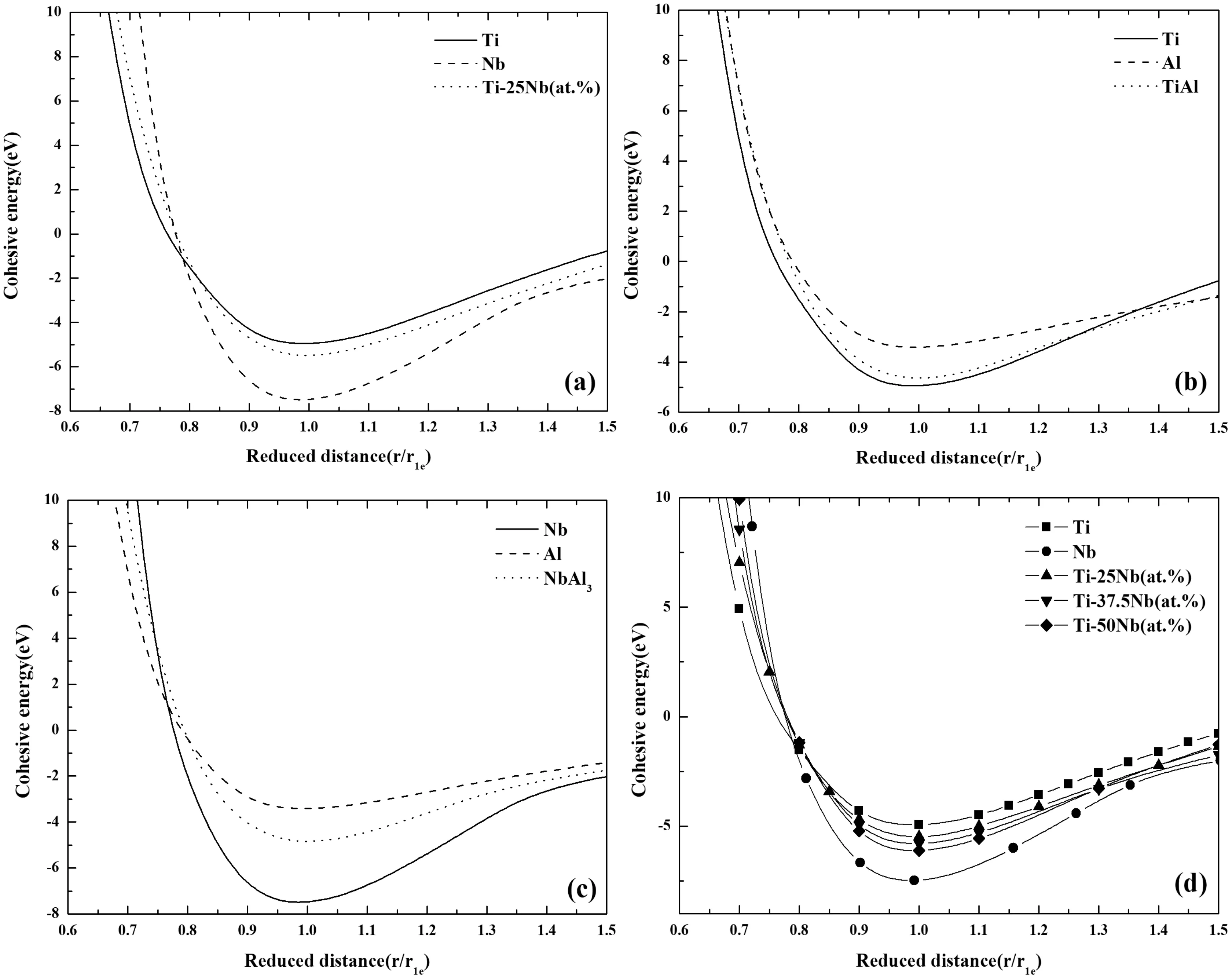
图3 二元合金体系的E-r曲线 (a) β相Ti-25Nb(at.%)合金; (b) L10结构TiAl合金; (c) DO22结构NbAl3合金 (d) Ti-Nb系合金对比Fig. 3 Comparison of E-r curves for the binary alloys: (a) β-phase Ti-25Nb (at.%) alloy, (b) L10 structure TiAl alloy, (c) DO22 structure NbAl3 alloy and (d) Ti-Nb alloy

根据上述表现出来合金E-r曲线与合金中元素含量的关系，我们猜想能否使用纯金属的E-r关系，通过合金中对应的比例转化数据直接得到合金的E-r关系. 以Ti-25Nb(at.%)合金为例，利用纯金属Ti和Nb的E-r关系，按照合金中对应元素的含量进行转化，得到的结果如图4所示. 从图中可以看到，使用第一原理计算得到的曲线(虚线)与使用纯金属E-r关系转化得到的曲线(实线)吻合的非常好，特别是在平衡态附近曲线几乎重合. 这表明这种方法是可行的，这也给为计算合金体系E-r关系提供了一种简单的方法，即利用第一原理计算纯金属的E-r关系，再通过合金中元素的含量，将纯金属E-r关系比例转化为合金的E-r关系.

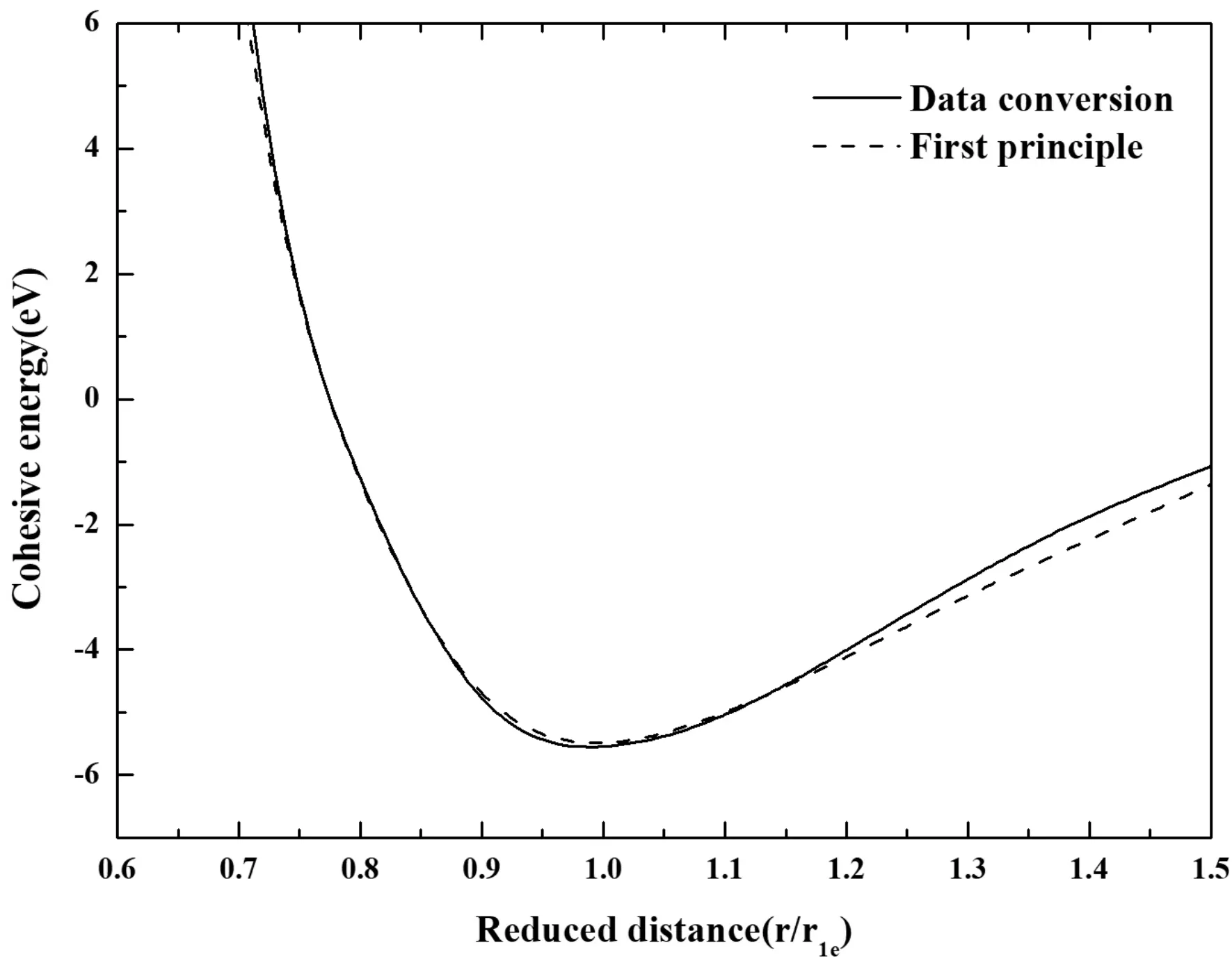
图4 使用不同方法得到的Ti-25Nb(at.%)合金的E-r曲线Fig. 4 The E-r curves of Ti-25Nb (at.%) Alloys obtained using different methods

3.3 态方程的应用——体弹性模量的计算

弹性模量是描写固体材料弹性形变表征力学性质的重要物理量，是选定机械构件材料的重要依据[25, 26]，也是用于拟合原子间相互作用势的重要参数. 采用本文中第一原理计算结果，通过最小二乘法拟 合曲线的方式计算体弹性模量. 选取的拟合函数为[27]：

(3)

式中Etot，E0，V，V0以及α分别为总能，平衡态能量，原子体积，平衡态原子体积和拟合参数. 体弹性模量由以下式子给出：

(4)

式中结合能E可由总能Etot与平衡态能量E0差得到，所以平衡态下：

(5)

从(5)式可以看到，拟合得到参数α即可得到体弹性模量. 上述方程使用的是能量体积关系，所以我们将上述E-r关系数据换算为E-V关系，使用数学软件包Mathematica编写程序拟合参数. 拟合过程中V0和E0选取实验值列于表2和表4中，拟合得到结果列于表3中.

表3 体弹性模量B0的计算结果

从体模量的拟合结果与实验值对比来看，我们发现拟合的结果与实验值相差10 Gpa左右，误差较小，拟合的结果很好. 长期以来实验数据一直是各类研究的参考依据，但是多种因素也影响着测定的准确性，所以理论计算材料物理性质是十分必要的. 从表3的拟合体模量结果的精确度来看，一方面检验了本工作中E-r关系计算的准确，另一方面，也表明使用这种方法计算材料体模量的可行性.

在文章中3.2节中提到，可以使用纯金属E-r关系按加权平均转换为合金的E-r关系. 为了进一步验证该方法的可行性，我们使用转化后的合金数据，最小二乘法拟合合金体模量，拟合所用到的实验值与拟合结果列于表4中. 对比表4与表3中合金体模量拟合结果可以看出，表4中的结果更接近实验值，拟合结果更好. 这说明使用纯金属E-r关系，按加权平均转换为合金的E-r关系的方法是可行的，并且使用该方法得到的E-r数据拟合体模量结果更佳.

表4 合金实验数据及其体模量拟合结果

Table 4 The experimental data and the fitting results about bulk modulus of alloy

Alloya(Å)c(Å)V0(Å3)E0(eV)B(GPa)Ti-25Nb3.273[28]—17.531055.64[32]115.503TiAl3.977[33]4.0565[33]16.04014.51[34]107.733NbAl33.80[35]8.75[35]15.793754.97[36]123.574

4 结 论

本文采用第一原理计算了纯金属Ti,Nb和Al及其二元合金的E-r曲线，计算并讨论了使用不同赝势对于不同的金属适用程度，及合金化元素的含量对该合金E-r关系的影响. 研究结果表明：

1)对于HCP结构的金属Ti和FCC结构的Al而言，使用GGA-PBE赝势计算其平衡态结合能的结果较为优异，比其他赝势计算结果更接近实验值. 而对于BCC结构的金属Nb而言，使用GGA-PW91赝势计算的结果与实验值更加接近.

2)纯金属E-r关系计算结果与结合能计算结果相吻合，相比之下使用GGA-PBE赝势计算Ti和Al的E-r关系与Rose的结果更加吻合，而对于金属Nb则使用GGA-PW91赝势计算得到的结果更佳.

3)合金E-r关系计算结果较好，曲线均处于其合金化元素曲线之间，并且，曲线会更靠近于含量较多的合金化元素的E-r曲线.

4)使用计算得到的E-r数据采用最小二乘法拟合得到的纯金属和二元合金的体弹性模量与实验值相比误差均较小，结果都很好.

5)可以使用纯金属的E-r关系，根据加权平均的方法计算合金的E-r关系，使用该方法得到的合金的E-r关系计算的体弹性模量与实验值非常接近.