变系数电报方程的紧致差分格式
杨文洁 姜子文
( 山东师范大学数学与统计学院,250358,济南 )
1 引 言
本文考虑如下的二维线性电报方程
(1)
其中α=α(x,y,t),λ=λ(x,y,t),Ω=[0,1]×[0,1]为R2平面上一个有界区域,∂Ω为Ω的边界,T为正常数,u0(x,y),v0(x,y)为已知函数.
电报方程是一类在通讯工程中有重要理论意义和广泛研究价值的数学物理方程,此方程是从研究电报线上电压和电流的变化规律推导出来的,它描述了均匀传输线上电压和电流的关系,所以又被称为传输线方程.对于求解电报方程的高精度数值方法,许多学者对其进行了讨论,其中文献[1]对于一维的常系数电报方程给出了高精度差分格式;文献[2]中则对电报方程初值问题构造了交替差分格式和交替方向有限元格式;文献[3]对一类电报方程的初边值问题建立了一种时间间断时空有限元格式;文献[4]描述了一类变系数电报方程的再生核数值解法.
紧致差分法是一类具有高精度的有限差分方法,是通过较少计算节点得到高精度的数值解,有效地减少了计算量和存储量.本文对方程(1)提出紧致差分格式,通过具体算例进行数值模拟,最后通过数值实验表明结果符合理论分析.
2 格式建立
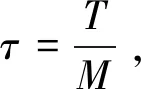
方程(1)在点(xi,yj,tk)处有
(2)
(3)
(4)
运用Taylor展式,结合(3)、(4)可得
`

(5)
其中
定义紧差分算子
(6)
由文献[5]中引理1.2有
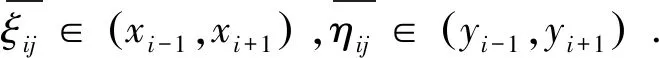
(7)
其中
由(1)式的初值条件及带积分余项的Taylor展开式有
(8)

3 数值模拟
下面将给出具体算例来验证格式的有效性.为了方便计算,将上述格式转化成
算例在方程中取α=0.02t(x2+1),λ=-0.02(y20+1),hx=hy=h,T=1,精确解u=t10sinπxsinπy,右端项F=(90t8+2π2t10+0.02t10(x2+1)-0.02t10(y20+1))sin(πx)sin(πy).
取不同空间步长和时间步长时L2和L范数下的误差和阶数,如表1所示.
表1 方程在L2和L范数下的误差和阶数
hτL2orderL谀order181641.26e-032.51e-0311612565.97e-054.591.18e-044.6213211 0243.37e-064.216.32e-064.31

