我国金融行业间风险相依性研究——基于隐马尔科夫混合Copula模型

吴 永，何 霞，郑文虎

(1.重庆理工大学 理学院， 重庆 400054； 2.西南大学 数学与统计学院， 重庆 400715)

随着金融经济的发展和创新，同一金融市场中的子行业相互关联和影响，在复杂化和多元化的金融市场中，某一行业发生极端风险，必定对其他行业产生冲击和影响，而其程度取决于他们之间的相依性大小。Forbes等[1]认为金融市场发生大的波动后，金融市场间的相依性显著增强可能导致风险的传染，所以需要研究对于同一市场，子行业间的相依性和它们之间是否存在着金融风险传染的可能。因此，本文对我国金融市场中的银行、保险、证券和信托行业间的风险相依性进行研究。

目前已有相关文献研究了我国金融行业间的相关性。李政等[2]选取了我国40家上市金融机构，运用无条件网络分析法研究了我国银行、保险和证券行业间的关联性；苏明政和张庆君[3]运用主成分分析、因果关系检验和网络分析的方法来研究我国银行、保险、证券行业间的相依关系和风险传染方向；王丽珍等[4]选取保险、银行、证券和信托四部门的上市金融机构,运用Granger因果网络模型来研究在两次牛熊市转化的极端情况下保险机构与其他金融机构系统相关性，实证表明银行业与保险业关联性最强；市场处于熊市时，保险业与其他金融机构存在着更显著的Granger因果关系。方意等[5]选取了26家金融机构，采用DCC-GARCH模型和随机模拟法研究了我国银行、保险与证券3个行业的动态相关性和系统性风险的测度。

上述文献均描述变量的线性相关性，金融变量却是非线性和非对称的，则描述金融变量非线性和非对称相关性的Copula模型得到较好的发展。随着其发展和壮大，实证研究表明，单一Copula模型并不能完全捕捉金融变量的所有尾部情况，因此Hu[6]首次将单一Copula函数线性组合成混合Copula，并运用于复杂金融市场相关性的研究。基于此，Jondeau等[7]将状态机制转换模型和混合Copula模型结合构建动态的混合Copula模型，研究了国际金融市场间的相依性；由于状态机制转换的模型只强调了状态间的转移，而忽略了状态的转移过程是以观测序列为条件的。因此，Chollete[8]在Copula的基础上引入了隐马尔科夫模型中，构建了二元隐马尔科夫混合Copula模型，并研究国际金融市场高低相关机制的相对重要性，但是该研究只停留于二元情形且正态Copula不能有效地捕捉金融行业的尾部相依性。

本文借鉴Chollete等[8]二元模型的思想，将混合Copula函数嵌套于隐马尔科夫模型框架，运用能捕捉尾部情况的阿基米德Copula来构建高维动态的混合Copula模型，并实证研究我国金融市场中的银行、保险、证券和信托行业间的动态相依性、高低相依状态的转换路径以及高相依状态下的尾部情况。

1 理论模型

1.1 边缘分布与混合Copula相依函数建模

1.1.1边缘分布模型构建

为了准确克服金融机构收益率序列的波动聚集性，本文采用Creal等[9]提出的广义自回归得分(GAS)模型。GAS模型是通过条件密度函数的分数驱动来描述数据的波动过程，其构建如下：设收益率yt的密度函数是p(yt|ft,Ft)，ft是时变参数，Ft为信息集，则GAS(1,1)模型为：

ft+1=w+αst+βft

(1)

st=St·▽t

(2)

(3)

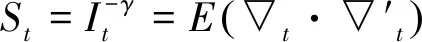
(4)

为了确定合适的边缘分布，检验上述各假设的边缘分布的拟合程度，检验分成两部分：其一利用拉格朗日乘子法判断GAS模型假设的条件分布是否可信，并通过直方图的置信区间标出；其二检验拟合分布函数的前4阶条件矩，根据前4阶矩的统计量和P值判断所拟合的分布函数是否独立同分布于均匀分布。

1.1.2混合Copula模型构建

混合Copula函数常见的构造是将阿基米德Copula族中的Gumbel Copula函数，Clayton Copula函数和Frank Copula函数线性组合，因为它们能捕捉不同的尾部情况。若选择单一函数，则只能反映金融变量的某一种尾部情况。因此本文用上述3种Copula函数构建d维混合Copula函数：设3种函数权重分别为w1、w2、w3，Copula分布函数分别为C1(u1,…,ud;θ1)、C2(u1,…,ud;θ2)、C3(u1,…,ud;θ3)，则混合Copula函数的分布函数为

(5)

(6)

经过整合，构建的混合Copula函数的似然函数表达式为：

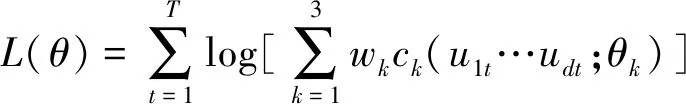
(7)

根据混合Copula密度函数的极大似然函数可以确定混合Copula函数的权重参数和相关参数，运用EM算法分离迭代估计上述参数。

1.2 隐马尔科夫模型(HMM)[11]

隐马尔科夫模型包含两个随机过程：马尔科夫过程和一般随机过程。马尔科夫过程描述的是隐状态的转移，一般随机过程描述的是隐状态与观察序列之间的关系，它以观测序列为条件，通过观测序列和隐状态间的转移概率矩阵构建双随机过程。Juang[12]认为隐马尔科夫模型可由4个参数描述：状态个数、初始概率分布、转移概率矩阵和观测序列的密度函数(3)若观测序列服从连续型分布，则用密度函数，若观测序列服从离散型分布，则用状态相关分布。(状态相关分布函数)。设隐马尔科夫过程{Xt}(t=1…T)有m个状态，d维连续型观测值序列{Yt}(t=1…T)在状态i时的条件概率密度函数为pi(yt)=P(Yt=yt|Xt=i)，初始概率分布π是初始时刻的无条件概率，则

π=[P(X1=1),P(X1=2),…P(X1=m)]

(8)

A是转移概率矩阵，其元素aij表示的是从状态i转移到状态j(j=1…m)的概率，因此，在任意t(t=1…T)时刻aij(4)当转移矩阵与时间t无关时，称为时齐马尔科夫过程，本文只考虑时齐马尔科夫过程。表示为

aij(t) =aij=P(Xt+1=j|Xt=i)

(9)

隐马尔科夫模型解决3个主要问题：

1) 评估问题：给定模型和观测序列，通过模型计算观测序列出现的概率。定义前向概率αi(t)=P(Y1=y1…Yt=yt,Xt=i)和后向概率βi(t)=P(Yt+1=yt+1…YT=yT|Xt=i)，并根据前向和后向算法计算观测序列的概率l=P(Y1=y1…YT=yT)得到，则

(10)

2) 解码问题：由于任意时刻的状态是隐藏的，因此需从中寻找任意时刻的状态，可通过Viterbi算法解决。若s1,s2,…,sT是最优状态序列，则

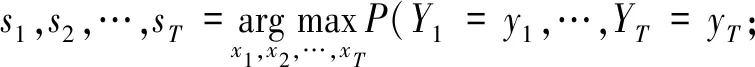
X1=x1,…,XT=xT)

(11)

3) 学习问题：最优化各个参数，使得最好的描述观测序列。EM算法是估计多个相关参数的最优选择。其中分为E步和M步，E步是对完全对数似然函数取条件期望，M步将条件期望最大化，从而得到最优参数值。

1.3 基于HMM的混合Copula模型

设3维{Kt}(t=1,…,T)是混合Copula函数的分支序列，分别代表t时刻样本用于Gumbel Copula函数，Clayton Copula函数与Frank Copula函数。据Sklar定理，t时d维联合密度函数f(y1t,y2t,…,ydt)满足

f(y1t,…,ydt)=

(12)

根据式(6)(12)，d维HMM完全数据的似然函数可以表示为：

L(φ,Y,K)=p(Y,X,K|φ)=

(13)

其中Y表示d维观测序列{Yt}；X表示m个状态的状态序列{Xt}；K表示3维分支序列{Kt}；参数族φ={πi,aij,wik,θik,ηh}(i,j=1…m;k=1…3;h=1…d)；θik是i状态时第k个函数的相依参数，ηh表示边缘分布参数。

令φ(r)是第r次迭代后的参数值，因此，对于E步，完全似然函数的条件期望Q(φ,φ(r))的第r+1次可以估计为：

Q(φ,φ(r))=E[logp(Y,X,K|φ)|Y,φ(r)]=

P(Xt=i,Xt+1=j|Y,φ(r))+

P(Xt=i,Kt=k|Y,φ(r))+

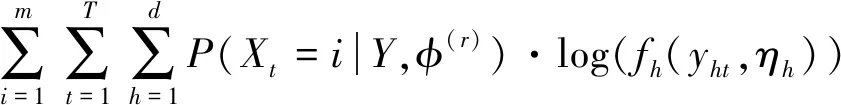
(14)

根据HMM模型中EM算法的估计步骤，记

γi(t)=P(Xt=i|Y,φ(r))

εij(t)=P(Xt=i,Xt+1=j|Y,φ(r))

在式(10)、αi(t)和βi(t)定义的基础上，γi(t)和εij(t)可化简为：

(15)

(16)

由于分支序列{Kt}与状态序列{Xt}独立，则

P(Xt=i,Kt=k|Y,φ(r))=

P(Xt=i|Y,φ(r))·P(Kt=k|Y,φ(r))=

(17)

将式(17)代入式(14)，则Q函数可简化为：

(18)

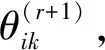
(19)

(20)

2 实证分析

2.1 数据选取与处理

由于行业股价指数的变动体现着一个行业的发展状况和市场环境的变化，那么行业的股价指数在一定程度上可反映该行业的整体水平，因此本文运用申万行业指数(5)根据申万指数编制规则，其是以申银万国行业分类标准为基础编制的分行业股价指数，是将行业内所有上市公司的股票作为成份股而构建的，它还结合了目前行业的发展现状及特点，表征该行业的平均股价变化，因此具有一定的代表性。中的银行、保险、证券和多元金融股价指数代表金融市场中的银行业、保险业、证券业和信托业。选取2010年9月1日—2018年4月4日的每日指数收盘价为样本，剔除交易时间不匹配的数据，得到每组样本数据共 1 844个，数据来源于锐思数据库，实证研究由R-3.4.1完成。

由于股价指数收盘价不平稳，因此对其取对数并差分后得到对数收益率(以下收益率均为对数收益率)，rit=100×(log(Pi,t)-log(Pi,t-1))，其中Pi,t表示第i行业第t日的股价指数收盘价，i=1,…,4，t=1,…,1 844。表1是行业日对数收益率的描述性统计量，可以看出证券业波动较大，其次是信托和保险，而银行业是四大行业中波动最小的行业，即银行业最稳定；行业收益率序列均“有偏”，除信托业左偏外，其他序列均右偏，表明各行业具有不同的尾部风险，且峰度系数均大于3，则具有“尖峰厚尾”等金融分布的典型特征；各收益率序列Jarque-Bera检验的p值均小于0.001，表明所有机构的收益率序列均拒绝服从正态分布的假设。

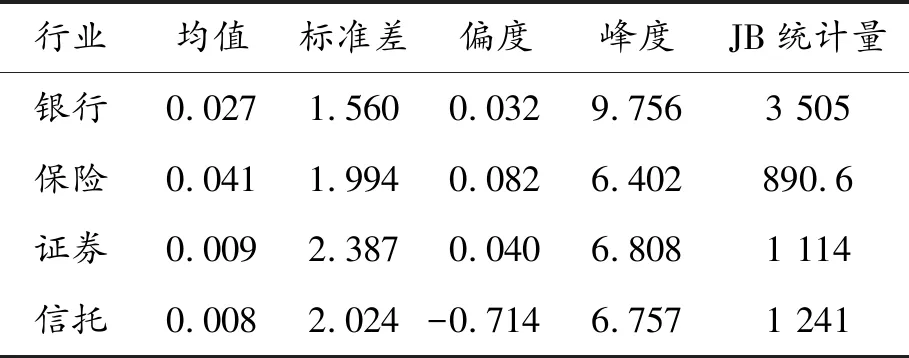
表1 金融子行业收益率的描述性统计量

2.2 边缘分布的确定

将收益率进行ADF单位根检验，结果显示在5%的显著水平下，4组收益率均为平稳序列。通过比较ARMA过程中不同阶数的最小信息化准则(AIC)，最终选择最优阶数为MA(1)模型来消除均值方程中的自相关性。其次考虑数据的异方差特性，对4组收益率的残差做ARCH效应检验，检验结果均拒绝原假设，表明数据均存在条件异方差性。因此，采用节1.1.1中GAS模型来克服其条件异方差特征，并得到GAS模型中参数的估计值，见表2。

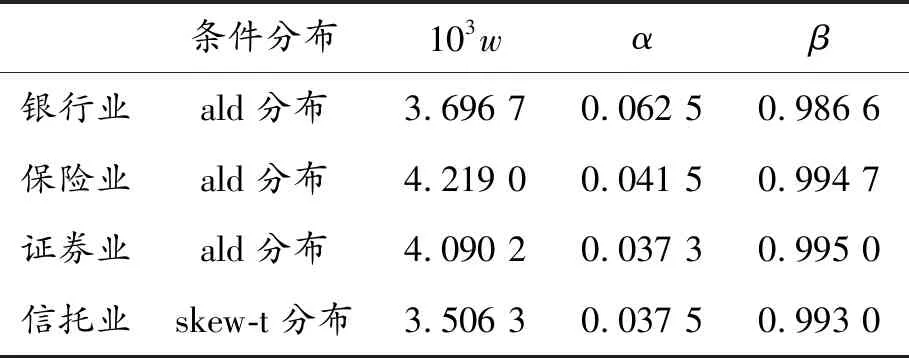
表2 GAS模型参数估计

从表2看出，只有信托业的条件分布服从偏t分布，另外3个行业均服从拉普拉斯分布(ald)，进一步证实了各序列具有一定的偏度，且信托和其他3组序列的尾部情况不同；4组序列的α均为正数，表明序列均以最快上升算法的方式递归；β均大于0.95，并接近于1，表明了序列的波动效应持久。

对上述得到的边缘分布进行检验，其一检验边缘分布所假设的分布是否可信，其二检验边缘分布能否在进行概率积分转换后独立同分布于均匀分布。图1是4组序列边缘分布对应的直方图结果，是在90%的置信水平上的拟合图，根据其直方图，除证券业的个别拟合点外，其他行业均在置信区间内，表明GAS模型中所得到的条件分布具有可信度。表3是概率积分转换的统计量和P值情况，根据表3，只有银行的3阶和4阶矩以及证券业的直方图的P值较小，但均大于0.5，且KS检验的结果均较好，表明通过GAS模型所拟合的边缘分布在概率积分转换后服从均匀分布。

图1 PIT拟合直方图

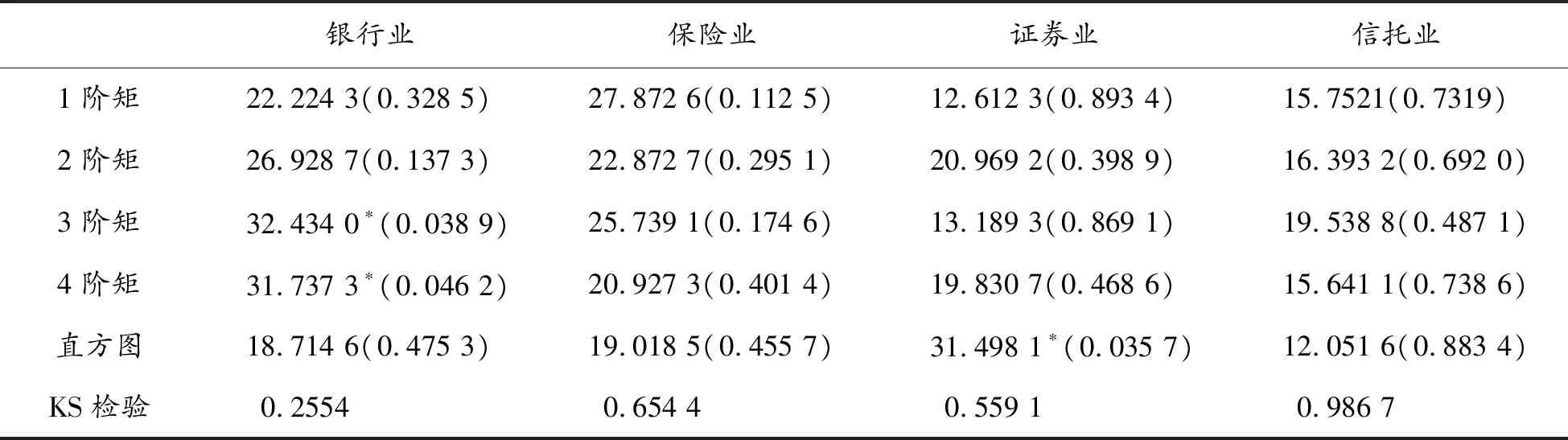
银行业保险业证券业信托业1阶矩22.224 3(0.328 5)27.872 6(0.112 5)12.612 3(0.893 4)15.7521(0.7319)2阶矩26.928 7(0.137 3)22.872 7(0.295 1)20.969 2(0.398 9)16.393 2(0.692 0)3阶矩32.434 0∗(0.038 9)25.739 1(0.174 6)13.189 3(0.869 1)19.538 8(0.487 1)4阶矩31.737 3∗(0.046 2)20.927 3(0.401 4)19.830 7(0.468 6)15.641 1(0.738 6)直方图18.714 6(0.475 3)19.018 5(0.455 7)31.498 1∗(0.035 7)12.051 6(0.883 4)KS检验0.25540.654 40.559 10.986 7

注：括号内的值是相应的P值，*表示在10%显著性水平下显著。

2.3 混合Copula模型参数估计

将边缘分布转换得到的均匀分布变量代入Gumbel Copula函数、Clayton Copula函数和Frank Copula函数以及混合Copula函数中，分别进行单一Copula函数和混合Copula函数的估计，混合Copula函数中相依参数θ的初值来源于单一Copula函数的估计值，选取w1=w2=w3=1/3作为混合Copula函数的初始权重，运用EM算法对其进行迭代，其中θ和w动态变化过程如图2所示。经过64次重复迭代后参数趋于稳定，相关参数值见表4。

图2 参数迭代图

通过对单一Copula和混合Copula的对数似然函数、AIC值与BIC值进行对比，根据对数似然函数最大，AIC、BIC最小的原则，表4表明混合Copula函数能更好地拟合数据；对于混合Copula函数的权重，Gumbel和Clayton Copula的权重相差不大，但Frank Copula的权重较小，表明金融行业间具有不对称的尾部情况，而Gumbel函数的权重稍大，表明行业间的上尾情况较明显，即一个行业股指的上涨引起另一个行业股指上涨的概率较大。

2.4 HMM的混合Copula模型估计

本文取高低两状态，分别对应着隐藏的行业间高相依性和低相依性，运用节1.3的模型对其建模。经过多次取值，初值的最终结果均相同，只是迭代速度不同，表明初始参数的选择只影响迭代速率，不影响最后结果，因此选择单一Copula函数的估计值作为HMM混合Copula模型的初始值，经过111次迭代后相关参数趋于稳定，其结果见表5。

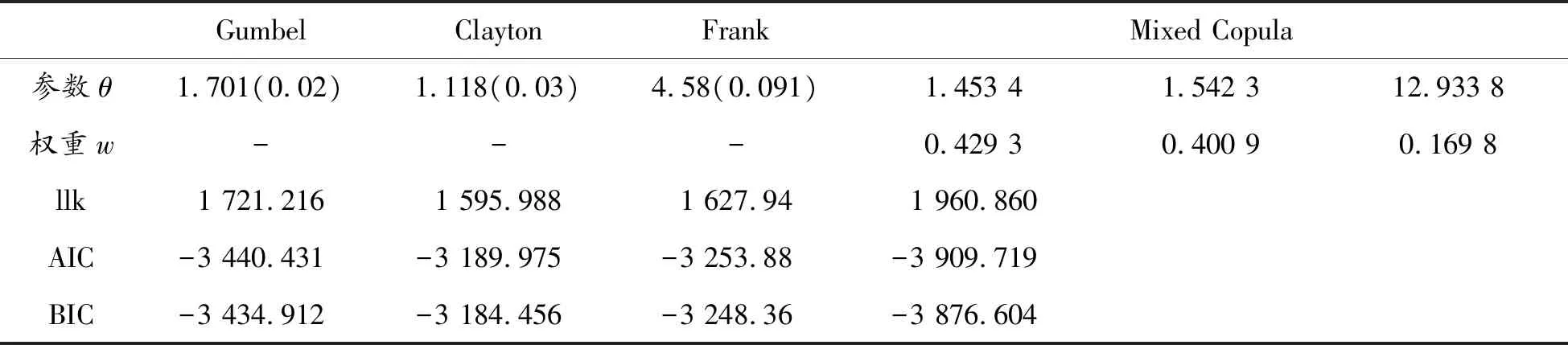
表4 混合Copula参数估计值

注：括号内是参数θ对应的标准差。

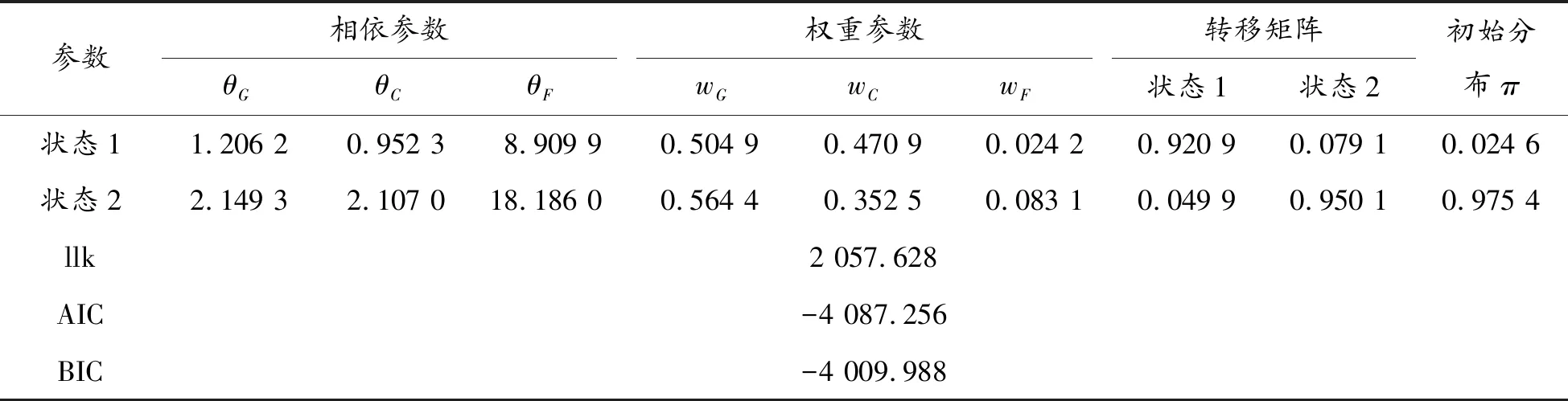
表5 HMM混合Copula参数估计值

表5所示，状态2的相依参数比状态1大，则状态2中四大行业间的相依程度更大，那么状态2为高相依状态，状态1为低相依状态。两状态均显示Gumbel Copula函数的权重最大，其次是Clayton Copula函数，Frank Copula函数的权重最小，表明了四大行业组成的金融行业的上尾相关性表现更明显，即四大行业同涨概率更大；处于高相依状态时，Gumbel Copula函数和Clayton Copula函数间的权重相差更大，说明行业间处于高相依性时，上尾情况较低相依时更为突出，即高相依状态时，行业间更易同涨。两状态自身转换的概率较大，其次低相依性向高相依状态转换的概率大于高相依向低相依性的转换，即该时刻行业间为低相依性，下一时刻是高相依性的概率较高，进而表明了金融行业是高相依性行业，这和金融行业的实际情况一致。初始状态为状态2的概率接近于1，表明了初始时刻四大行业间处于高相依性。通过对表4与表5中4种Copula函数的对数似然函数、AIC和BIC结果的比较，说明在隐马尔科夫模型中嵌入混合Copula函数得到的动态混合Copula模型相比混合Copula和3个单一Copula函数更优，这与淳伟德等[14]的研究结论一致。

行业间高相依性和低相依性的状态是隐藏的，其可由节1.2中的Veterbi算法进行解码，得到样本区间的最优动态转换路径图(图3)。

图3 HMM混合Copula的两状态动态转换

图3显示，高低相依状态以一定的频率进行转换，但其频率并非固定，高低相依转换的频率对应着金融行业间相依性程度的强弱。结果还显示，样本区间内我国金融行业的高相依性持续时间较长，主要发生于以下时间段：① 2011年5月—2012年5月。自交通银行入股太保康联后，2011年银邮代理寿险公司占比达到84.7%，银邮保费收入占比近50%[15]，相比2010年分别增加了11.77%和5%，使得银行入股保险公司进入“小高潮”，这促进了银行和保险的深层次合作，使得金融子行业间的相依性增强；② 2013年5月—8月。5月下旬光大银行同业违约的传闻使得钱荒出现，央行的意外之举，使得原本作为资金拆借的商业银行进入借款大军，银行间拆借利率飙升，随后央行并没注入流动性，于是钱荒事件达到高潮，资金流动性紧张的影响蔓延至整个金融市场，使得各行业联系紧密；③ 2014年5月—2014年10月。在经济疲弱、股市低迷的市场态势下，我国发布了针对完善我国资本市场的新“国九条”政策，该政策鼓励金融市场多元化、产品创新化，以及培育私募市场，增强了股民对投资市场的信心，化解了市场资金的流动性问题，使得各行业紧密相连；④ 2015年6月8日—7月10日和8月1日—8月26日，持续时间并不太长。6月15日股市出现大跌，直到7月8日创下最低收盘价，跌幅达32%，基金公司开户和券商收益均减少,银行、信托中达平仓线的股票比例上升[16]，8月16日—8月26日出现了第二轮的下跌，跌幅达到了29%，上市公司大量停牌，人民币也开始暴跌，最后引发了一场严重的股灾，使得金融各行业的股票指数趋同性增加；⑤ 2015年10月底—2016年2月底和2016年4月中旬—2016年7月初。从2015年11月开始，人民币开始慢慢贬值。12月美联储加息后人民币加速贬值，2016年初，中国股市也出现了巨大的波动，多次暴跌甚至出现熔断停盘现象，私募基金也严重受挫，国内市场资金短缺。第二季度后，人民币贬值和英国脱欧事件不断对国内市场带来冲击和扰动，国内债券也出现违约潮，使得市场发生大的波动和各行业的股票指数联动性增强。根据Forbes和Rigbon[1]，相依性的增强可能导致风险发生传染，则这些时段发生风险传染的概率较大，因此，所建立的动态模型能有效捕捉金融重大事件。

图4是分别处于高和低相依状态的连续条件概率图(上图是低相依状态概率图，下图是高相依状态概率图)，比较图3和图4，发现概率图与行业间的高低相依性动态转换图一致，行业处于某相依状态时，某相依状态的条件概率大。从图3、4中同时可以看出高相依状态的持续时间更持久，这也说明了金融事件发生期间对应着行业间的高相依状态。因此，当金融行业处于2状态时，行业间具有更高的相依关系，那么发生金融风险传染的概率较大。

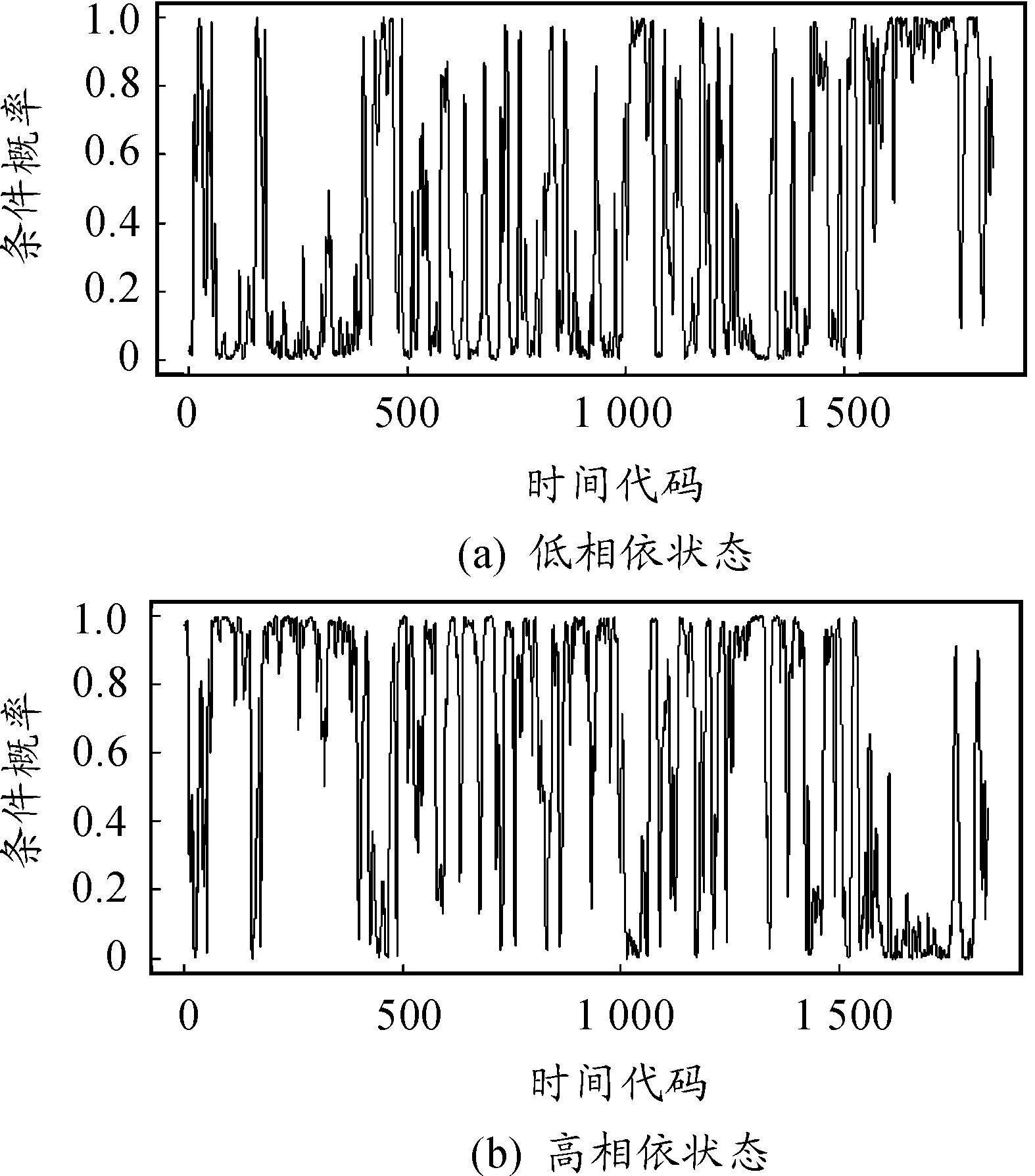
图4 HMM混合Copula的高低状态条件概率

2.5 两状态的尾部相关性分析

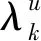
(21)

表6中，两状态下银行业和保险业上尾与下尾相依系数均最大，即表示任何时期，银行业和保险业尾部相关性均最强，则共同发生极端事件的概率最大，那么它们之间的相互冲击和影响也最大，其次是银行业和证券业，其他3个行业与信托业的尾部系数均相对较小；高相依状态下的行业尾部系数均大于低相依状态下的尾部系数，说明行业处于高相依状态时更易发生尾部风险，这与金融市场相一致；除了银行业与信托业，行业间的上尾相关系数均大于下尾相依系数，说明金融四大行业处于高相依状态时，上尾风险较大，该结论和表5中显示的高状态相依情况下上尾更突出一致。

表6 高相依状态下行业之间的尾部系数

3 结束语

本文在隐马尔科夫框架上嵌套混合Copula模型，构建了动态混合Copula模型，并研究我国金融四大子行业间的非线性动态相依关系以及尾部情况，结果表明：其一，将构建的HMM混合Copula与3种单一Copula、混合Copula模型相互比较，HMM混合Copula模型更优，它能较好地表现出金融行业间的动态相依状态和动态转换路径，还能捕捉我国重大金融事件的发生，表明了所构建的模型具备了混合Copula和隐马尔科夫状态动态性的双重优点；其二，高相依状态时，我国金融子行业间的相依性较强，风险传染的概率较大，则从相依性和传染的角度看，可能会引发宏观或系统性风险的发生；尾部情况表明高状态下的金融行业间的尾部风险更大，此时银行和保险业对彼此冲击的敏感性较大，且更易受到对方冲击的影响。