火箭助推零长发射建模仿真研究
张 琳,龚喜盈,张晓辉
(西安爱生技术集团公司,西安 710065)
0 引言
火箭助推技术最早用于发射无人机是在1956年秋,苏联利用火箭助推器发射了SM-30 无人驾驶遥控飞机[1]。国内外有很多成熟的无人机系统采用火箭助推零长发射的起飞方式。例如,ASN-209、ASN-215、WJ-500 等采用机身下方单发火箭助推发射。俄罗斯La-17 靶机和意大利米粒奇-300/600 等采用机翼下方双发火箭助推发射[2]。
采用火箭助推方式发射起飞的无人机,起飞阶段风险性大,因此,为确保发射阶段的安全性,需要建立其仿真模型平台,真实反映无人机起飞运动状态,为发射阶段提供重要的参考依据。
1 仿真过程描述
无人机发射阶段受力以及运动非常复杂,本文以某无人机为研究对象,通过在Matlab/simulink 中建立无人机六自由度非线性力学模型、飞行控制系统模型、控制指令模型、助推火箭模型、发动机模型、重力模型、标准大气模型、舵机模型等,对其火箭助推发射阶段进行仿真研究。确保仿真过程中火箭工作结束时无人机具有相应的安全速度和安全高度,同时发射阶段无人机的姿态变化要相对平稳。
火箭助推器内燃料的燃烧可以在非常短的时间内使无人机获得巨大的动能[3],在几秒的作用时间内使无人机速度迅速增加。采用火箭助推方式发射起飞的无人机,需要根据飞机的重量和气动特性,选取合适总冲的助推火箭,保证在火箭推力作用结束后,无人机达到其安全速度和安全高度。火箭推力作用结束后,由于自身重力,火箭自行脱落,无人机在发动机推力的作用下继续爬升[4]。
在发射过程中需要考虑由于火箭燃料的消耗以及火箭脱落前后飞机重心位置的变化。在发射过程中火箭脱落前后的状态相比,脱落前的状态无人机重心位置会偏后下方,使得无人机静稳定裕度降低。当重心位置过于靠后时,会造成无人机纵向姿态振荡[5]。同时由于发射初始短时间内动压较小,气动力较小,因此,发动机螺旋桨的反扭矩以及火箭推力线与无人机重心的相对位置关系,对于发射初始阶段姿态变化起着决定性的作用。随着动压的增大,在控制系统作用下通过控制舵面的偏转,可以完成飞行姿态的控制。如图1 所示。
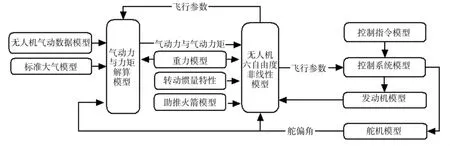
图1 仿真系统结构框图
2 发射过程无人机所受外力与力矩
在无人机发射过程中,受到的外力包括:重力、气动力、螺旋桨作用力、助推火箭作用力及力矩,具体表示如下:

其 中,F 为 机 体 轴 上 的 合 外 力;Gb、Faero、Fprop、Fnormal、Frocket、FRU分别为重力、气动力、螺旋桨推力、螺旋桨法向力、火箭推力、火箭分离力在机体轴系的分量;M 为 绕 机 体 轴 的 合 力 矩;Maero、Mcg、Mprop、Mnormal、Mf、Mrocket、MRU分别为气动力矩、气动参考重心到实际重心的折算力矩、螺旋桨推力力矩、螺旋桨法向力力矩、螺旋桨反扭矩、火箭推力力矩、火箭分离力力矩。发射过程中相关参数的定义参见图2。
2.1 火箭作用力与力矩
火箭推力线一般不通过无人机重心位置,因此,火箭安装角(αrocket为火箭推力线与机体OXZ 平面的夹角,βrocket为火箭推力线与机体OXY 平面的夹角)和火箭推力线与无人机重心位置之间的相对位置关系至关重要。
火箭推力在机体轴中表示为:

火箭推力绕机体轴的力矩表示为:

图2 飞机受力示意图
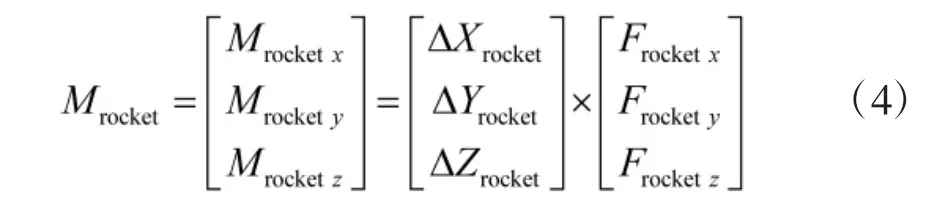
其中:

火箭推力作用点位置为Procket=(Xrocket,Yrocket,Zrocket);实际重心位置为PGG=(XGG,YGG,ZGG)。
2.2 火箭脱落阶段分离力与力矩
助推火箭与无人机采用锥体、锥窝对接接头连接方式,在助推火箭推力接近消失时,火箭在其重力作用下与飞机分离,分离过程短暂[6]。
以火箭为研究对象进行分离过程受力分析参见图2,锥台对火箭的作用力为FUR;火箭AB 长度为lrocket;火箭重力Grocket作用于重心C;AC 长度为lGr;火箭转动惯量为Irocket;火箭重力方向与火箭轴线的夹角为δ;arz为火箭z 方向线加速度,单位为m/s2;为火箭俯仰角加速度,单位为rad/s2。
把火箭作为刚体,其运动方程为:

由上述方程组得到锥台对火箭的作用力FUR,因此,火箭对锥台的作用力FRU为:

FRU与机体纵轴夹角为η(η=δ+θ)。由此得到FRU在机体轴的分量:
由火箭安装点与无人机重心之间的相对位置关系得到分离力产生的绕机体轴的力矩MRU:
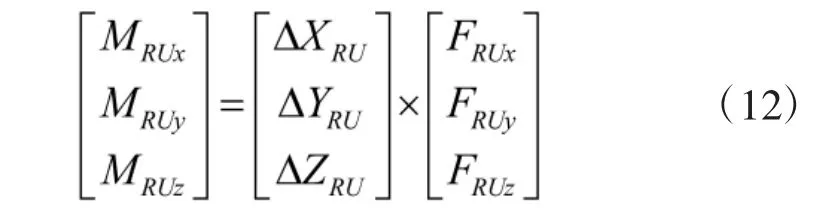
2.3 螺旋桨推力、法向力与反扭矩
飞行中气流斜吹过桨盘时,除了产生推力,还会产生法向力,该力大小与升力成正比,方向与升力相同[7]。在发射初期迎角为负,前拉式螺旋桨的法向力产生低头力矩,后推式螺旋桨的法向力产生抬头力矩。小迎角时,前拉式螺旋桨的法向力起静不稳定作用,后推式螺旋桨的法向力起静稳定作用。
发射过程中螺旋桨的转动会产生与旋转方向相反的力矩称为反扭矩。该力矩可通过舵面偏转来纠正,亦可通过调节火箭的侧向安装角来使火箭产生与反扭矩方向相反的力矩,以此抵消反扭矩。在发射初期速度较低时,舵效较低,因此,调节火箭安装角对于横航向姿态的调整起着重要的作用。
发动机安装角为αeng,发动机推力在机体轴中表示为:

发动机推力的力矩表示为:

其中:

螺旋桨安装点位置为:Pprop=(Xprop,Yprop,Zprop)。
螺旋桨的法向力Fnormal由CFD 计算或螺旋桨风洞试验得到,进而求得法向力产生的力矩Mnormal=Pprop×Fnormal。螺旋桨产生的反扭矩为Mf=p/n,其中,p为发动机输出功率,n 为螺旋桨转速。
2.4 无人机气动力与力矩
其中:

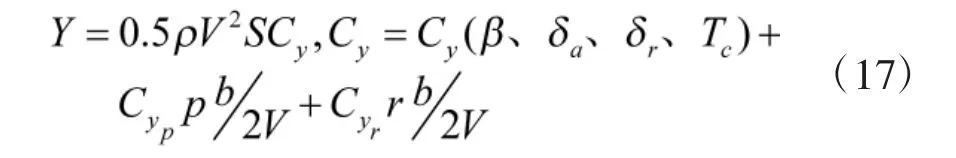
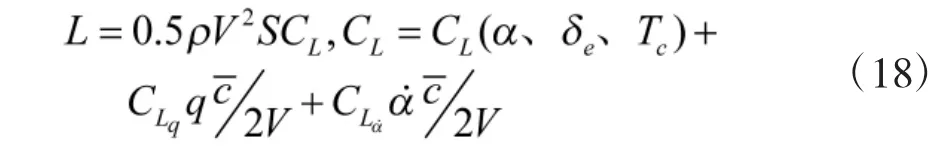

其中:


气动参考重心到实际重心的折算力矩Mcg为:

其中:
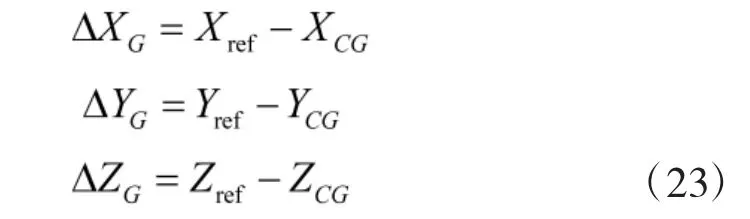
气动参考重心位置为:Pref=(Xref,Yref,Zref)。
2.5 重力数学模型
对于非对称飞行,重力对速度、气动迎角和侧滑角有较大的影响。重力在地轴系和机体轴系中使用矩阵形式来表达,重力在地轴系表达为:G=[0 0 mg]T,在机体轴系的表达为:Gb=LBG[0 0 mg]T,LBG为地轴系到机体轴系的转换矩阵。
3 纵向和横航向控制系统
由于助推火箭推力不对称和螺旋桨反扭矩,发射过程中可能出现大的纵向俯仰姿态变化,同时横向滚转姿态变化既而产生无人机偏航。因此,控制策略上应尽量保持无人机姿态的稳定,不要出现过大的姿态变化[8]。
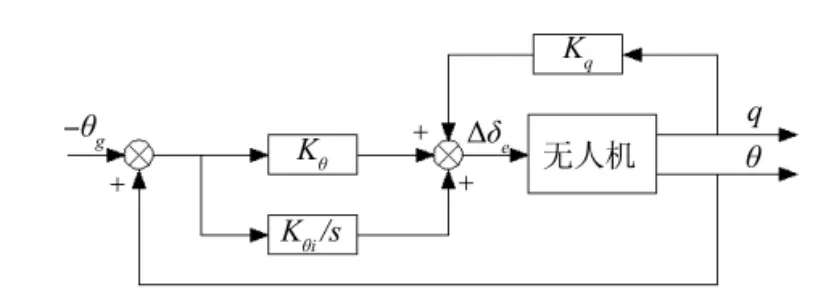
图3 纵向控制系统结构图
纵向控制系统采用俯仰角控制回路来增加系统阻尼,控制纵向姿态。俯仰角控制回路中将俯仰角速度、俯仰角和俯仰角积分反馈到升降舵。俯仰角速度反馈用来增加系统俯仰阻尼,从而改善纵向品质特性;俯仰角反馈用来控制稳定俯仰姿态;俯仰角积分反馈用来提高俯仰姿态控制精度,消除姿态静差。纵向控制律结构如下:

横航向控制系统采用滚转角控制回路来增加系统阻尼,控制横向姿态。无人机需要改变航向,仍然需要滚转角控制,只有控制无人机达到需要的滚转角才能产生需要的侧力使得航向得到改变。滚转角控制回路中将滚转角速度、滚转角和滚转角积分反馈到副翼。滚转角速度反馈用来增加滚转阻尼,使得滚转角得到平滑的过渡;滚转角反馈用来控制稳定滚转姿态;滚转角积分反馈用来提高滚转姿态控制精度,消除姿态静差。横航向控制中将偏航角速度反馈到方向舵来增加航向阻尼。横航向控制律结构如下:


图4 横航向控制系统结构图
4 仿真结果与分析

图5 速度变化仿真曲线

图6 高度变化仿真曲线

图7 滚转角变化仿真曲线

图8 俯仰角变化仿真曲线

图9 偏航角变化仿真曲线

图10 升降舵变化仿真曲线

图11 副翼变化仿真曲线

图12 方向舵变化仿真曲线
针对某火箭助推零长发射无人机,由海平面高度发射起飞,发射重量200 kg,发射角θlaunch=15 deg,助推火箭总冲为6 000 N.s,作用时间为2 s。该无人机发射后在助推火箭推力作用下离架,火箭推力作用结束后,无人机应达到其安全高度与安全速度,进入爬升阶段,开始定俯仰姿态爬升,姿态角控制指令为15 deg。完整零长发射过程仿真结果见图5~图12,由仿真结果分析得到:1)在火箭脱落后无人机达到安全速度V=120 km/h,此速度大于失速速度并留有一定的安全裕度;随后无人机以V=110 km/h的速度继续爬升;2)在火箭脱落后无人机达到安全高度H=10 m,随后继续爬升,在20 s 的时间内无人机可达到160 m 的高度;3)无人机俯仰角由初始发射角15°开始变化,最大俯仰角接近18°,爬升阶段在控制系统作用下以14.5°俯仰角爬升;由于螺旋桨反扭矩使得无人机发射后右滚,最大滚转角为6°,在控制系统作用下滚转角回到稳定值2°;由于在发射过程横航向没有设定偏航角的目标值,在20 s 内偏航角为16°;4)整个发射过程舵面偏转量在合适的范围内,最大升降舵偏角为5°,最大副翼偏转角为10°,最大方向舵偏转角为1.5°。
5 结论
仿真曲线给出了火箭助推零长发射的完整过程。参考仿真结果,判定无人机速度和高度是否达到安全速度和安全高度;姿态变化是否平稳可控;同时舵面偏转量是否小于设定的最大用舵量。上述情况同时满足时,即认为整个发射过程是安全可控的。在后续建模仿真研究中,可以建立舵机、传感器等的物理模型,更好地精细化、精准化仿真模型。

