基于线性预测的雷达航迹压缩算法

马天林，韩壮志

（陆军工程大学石家庄校区，石家庄 050003）

0 引言

雷达能够对空中目标实现连续侦测，获取敌机的位置、速度、高度等飞行参数，形成具有一定格式的雷达航迹数据。目前可移动雷达航迹数据传输以无线电台和有线通信为主。但有线通信传输距离受限，无线电台易受干扰。由于北斗短报文具有通信可靠、稳定、保密性强等优点［1-2］，所以在无线电台和有线通信遭失效的情况下，北斗短报文通信可以成为重要的应急传输手段。北斗短报文通信已经在电能数据采集［3］、电网监测系统［4］和油田监测［5］等方面得到广泛应用。但北斗短报文通信带宽有限，难以实现常规雷达航迹数据的传输。在此情况下，数据压缩是一种有效的解决途径。

雷达航迹压缩的特点是小数据量压缩。根据数据率的不同，每个雷达航迹信息包含的点迹数据量也各不相同，通常为6 个～12 个/min 点迹，数据量较小。常用的压缩方法有无损数据压缩、专用数据压缩、曲线拟合压缩和特征点压缩。无损数据压缩一般基于大数据量的文本数据进行压缩［6］，对于小数据量的雷达航迹，压缩率常常大于100%。对于应用于图像和视频的专用压缩算法，例如小波变换［7］、压缩感知［8］等，并不适用于雷达航迹压缩。曲线拟合参数压缩和特征点压缩是通用的小数据压缩算法。曲线拟合参数压缩对点迹进行曲线拟合，进而传输曲线参数实现点迹的压缩。文献［9］提出一种基于二阶多项式拟合的雷达点迹压缩算法，但它仅适用于航迹为直线和近似抛物线的情况，其他情况下误差较大。特征点压缩算法通过提取的特征点代替点迹传输实现点迹的压缩。特征点压缩算法主要包括间隔取点法、合并法（偏角法）、垂距法［10］、分裂法［11］以及预测法［12-14］等。间隔取点法等间隔的取点作为特征点，算法虽然简单，但误差较大；合并法通过夹角的大小确定是否舍去该点，算法运算量较大；垂距法根据点到前后两点连线的距离来判断是否选取该点，恢复点迹误差较大；分裂法取到首尾两个点组成的直线距离最大的点，将直线分裂为两段，然后递归的使用分裂法，直到所有的点处理完，该算法运算量大；文献［12］基于死区原则对数据进行线性预测实现触觉点数据压缩；文献［13］基于多自由度死区原则对数据进行线性预测实现触觉点数据的压缩；文献［14］基于最小二乘和中值滤波对数据进行线性预测实现触觉点数据的压缩。但是死区原则和中值滤波并不适用于航迹数据的预测，本文采用设置误差阙值对航迹数据进行线性预测，实现对航迹数据的压缩。

1 线性预测的分段拟合压缩算法

基于线性预测的分段拟合压缩方法将点迹数据组成的航迹进行分段，对每一段进行最小二乘直线拟合。如果目标不做机动，直接用直线进行拟合；如果目标做机动，在一定误差范围内，可以用折线对航迹进行拟合。相比于其他函数进行拟合，直线拟合的运算量小，运算简单。基于线性预测的分段拟合压缩算法，采用的分段方法是用拟合的直线进行点的预测，根据实际情况设定误差阙值，通过判断预测的点与真实点之间的距离与误差阙值的大小关系来确定是否分段，最后选取每段直线的端点和首尾点作为特征点实现点迹的压缩。

由于目标的航迹是一个三维曲线，因此，采用三维折线拟合三维点迹。对于空间中的直线，可以看作两个平面的交线，所以可以用一个方程组来表示空间直线：

根据最小二乘原理，使残差的平方和最小［15］，可得：

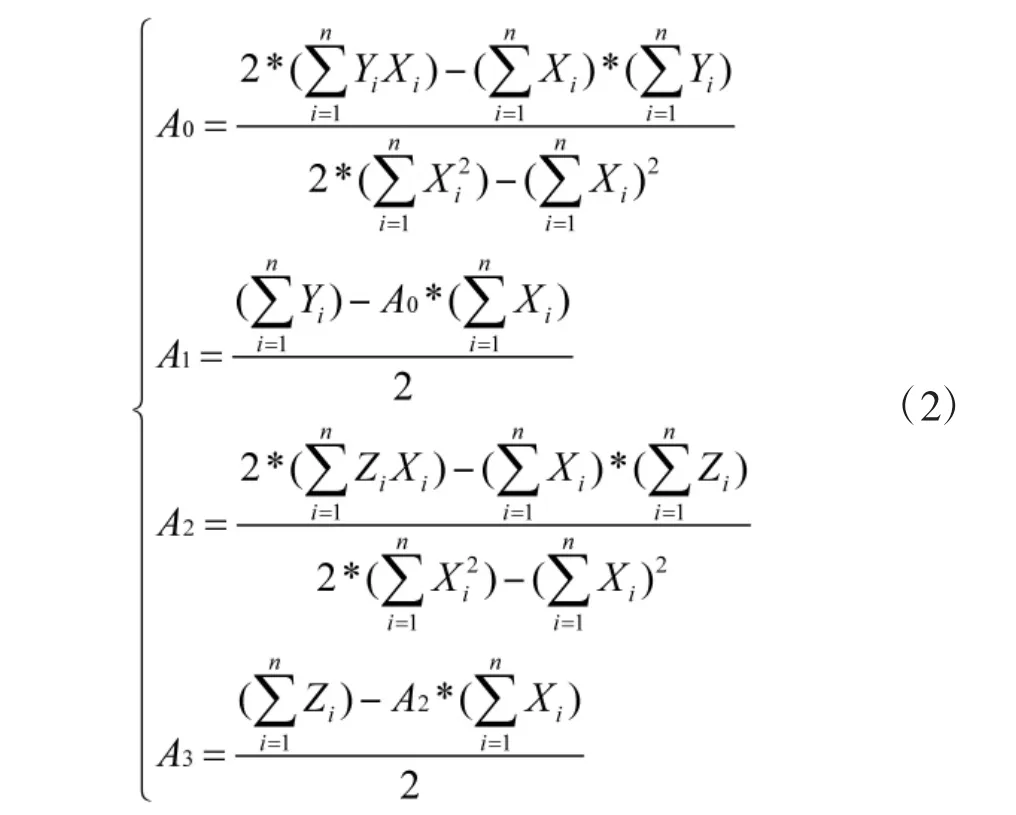
线性预测分段拟合压缩算法的步骤如下：

1）记一批航迹共有n 个点，记为Pr1，Pr2，…，Pri，…，Prn其中Pri的坐标记为（Xi，Yi，Zi）。对前3 个点用三维最小二乘法进行直线拟合，Pr1，Pr2，Pr3得

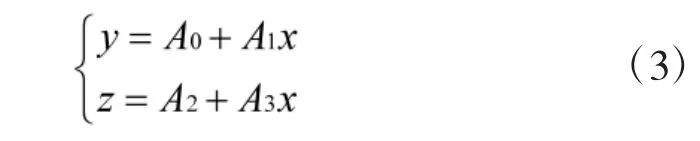
2）在假设目标做匀速运动的前提下，基于前3个点预测下一个点的横坐标Xp1为：

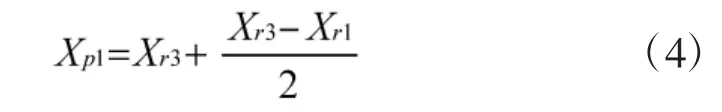
根据式（4）得预测点的其他坐标Yp1，Zp1为：

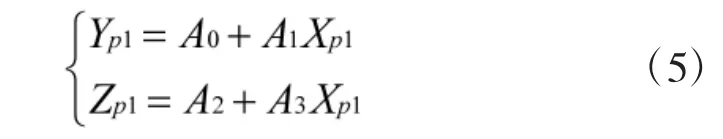
3）将预测得到的点Pp1（Xp1，Yp1，Zp1）与后续的点Pr4间的距离l 与误差阙值d 比较，如果点Pp1（Xp1，Yp1，Zp1）与后续的点Pr4间的距离l 小于误差阙值d，则忽略该点，进行下一个点的预测；如果点Pp1（Xp1，Yp1，Zp1）与后续的点Pr4间的距离l 大于误差阙值d，则记录该点，并取下两个点，拟合新的直线，重复1）～3）；

4）通过以上步骤处理点迹，直到所有的点处理完，确定每段直线的端点；

5）确定好每段直线的端点，用这些端点作为这些点的特征点进行传输，从而实现点迹数据的压缩。

线性预测的分段拟合压缩算法流程图如下页图1 所示。

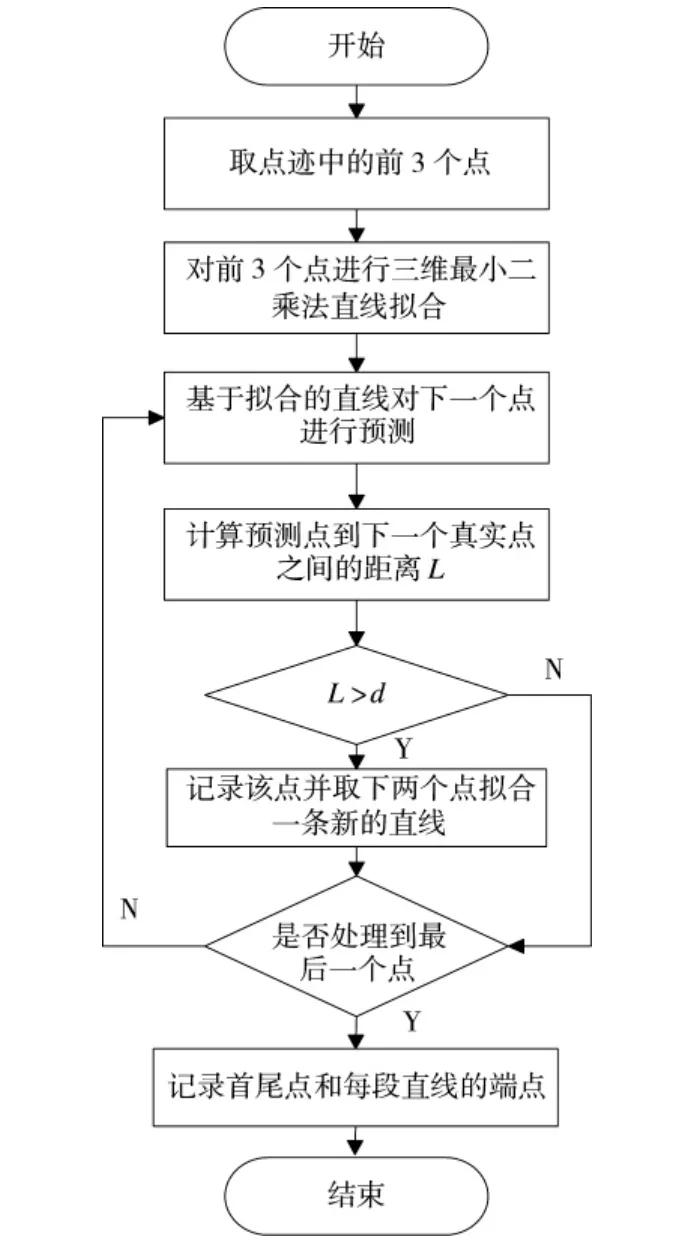
图1 线性预测的分段拟合压缩算法流程图

2 仿真实验及效果评估

2.1 仿真实验

某警戒雷达一分钟转12 周，对其实测的目标数据进行压缩仿真，其中设定的误差阙值d 为1 km，该目标因为地理原因作了一次转弯机动，其高度、距离、方位如表1 所示。

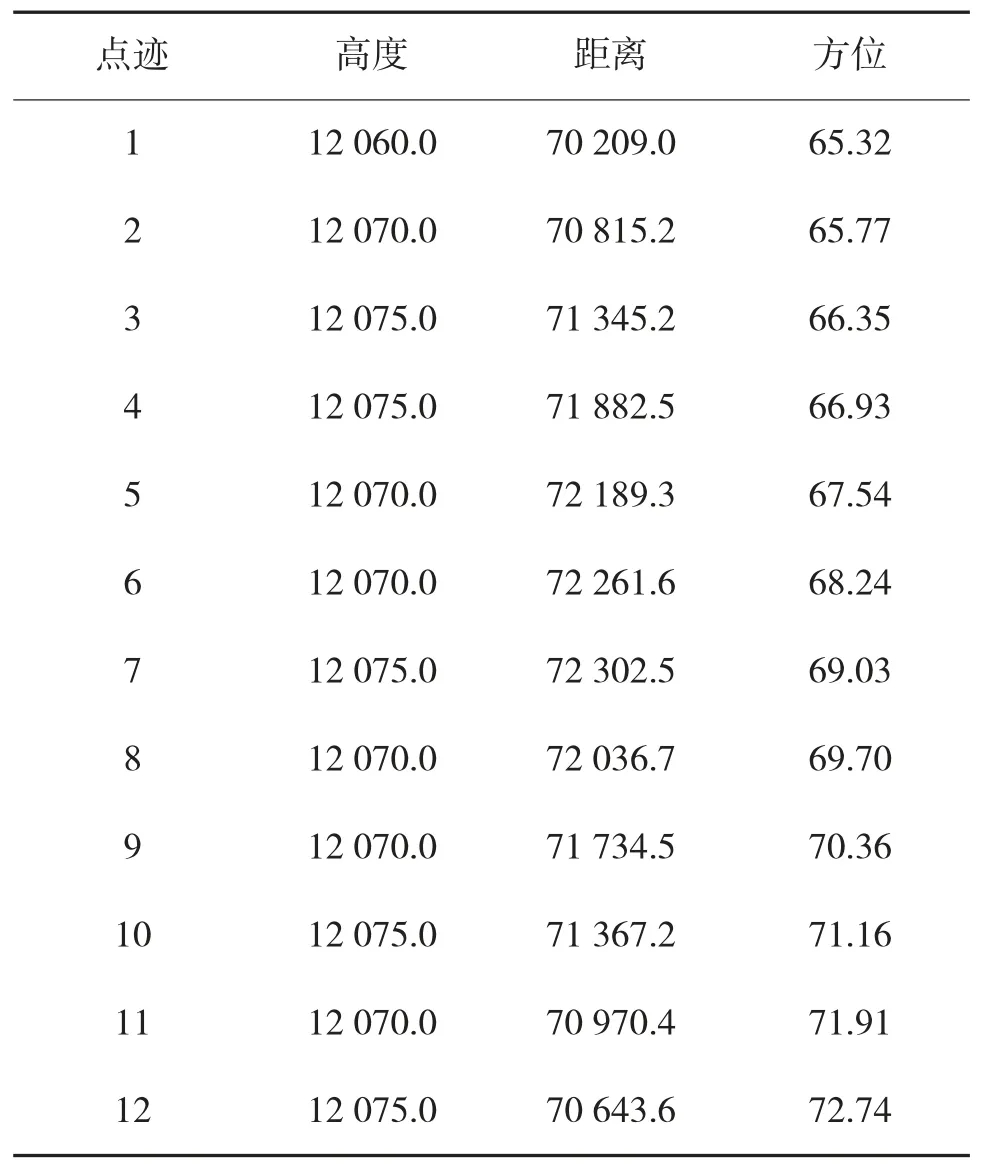
表1 雷达探测的某目标参数

对警戒雷达探测的目标航迹分别用垂距法［10］、分裂法［11］、分段直线和二阶多项式［9］进行拟合。拟合结果如图2～图5 所示。

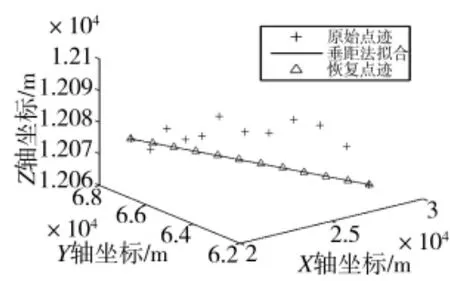
图2 垂距法拟合

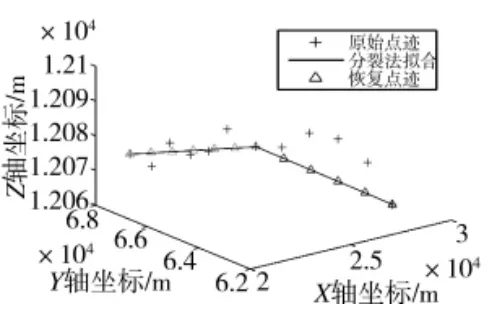
图3 分裂法拟合

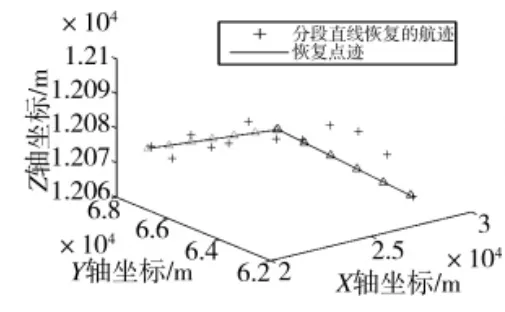
图4 分段直线拟合

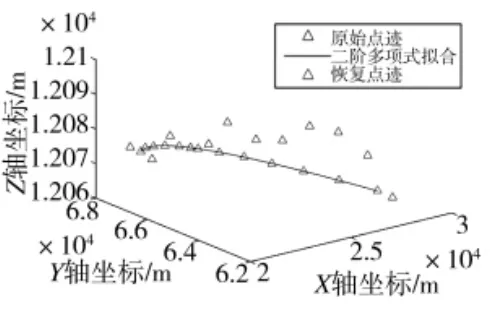
图5 二阶多项式拟合

2.2 压缩效果分析

在本试验中，为了对算法进行优劣分析，从运算量、误差和压缩率3 方面对算法进行比较。

运算量表征了算法的复杂程度，运算量越大，算法的复杂程度越高，系统延时也就越长，对硬件提出的要求越高，为了比较算法运算量，将不同算法在同样的运行环境下进行仿真，本文在MATLAB R2014b 中进行运行仿真，运行时间如表2 所示。

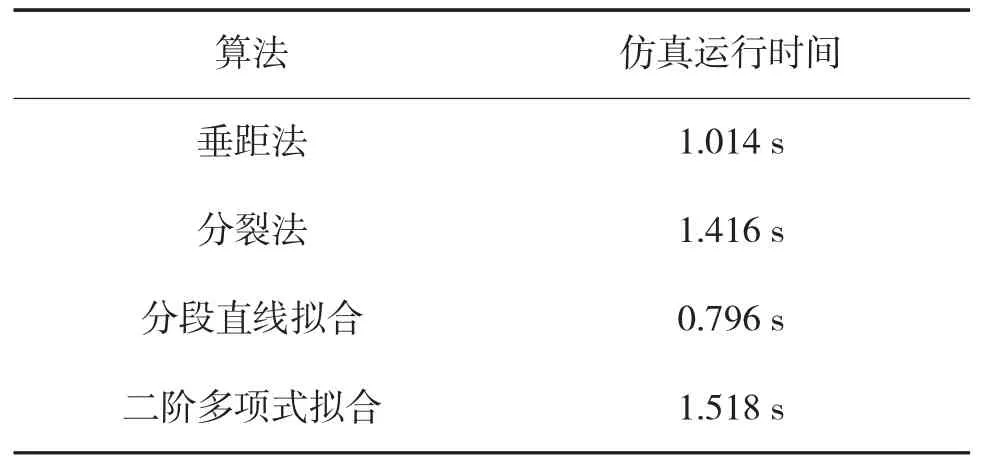
表2 算法仿真运行时间

由表2 可知，基于直线预测的分段直线拟合算法运行时间相较于其他算法最短，运算量最小，算法的复杂程度低，对硬件的要求低。

误差是衡量算法优劣的重要标准，误差越小，就越能表征目标的真实运动情况。采用真实点迹与恢复点迹之间的距离表示误差e，恢复点迹采用单周恢复法。其中

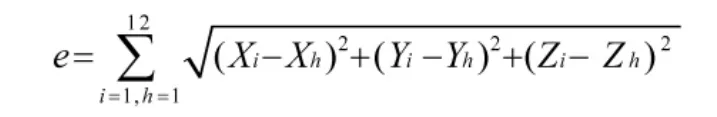
其中，（Xi，Yi，Zi）表示原始点迹，（Xh，Yh，Zh）表示恢复点迹，为了比较误差大小，分别用不同算法的误差与分段直线拟合的误差相比，结果如下页表3 所示。

由表3 可得，分段直线拟合的误差最小，恢复的点迹与真实点迹最接近。

压缩率直接表征了算法的压缩效果，一共传输了12 个点迹，标准情报格式每个点迹占用13 Byte，如果不采用压缩直接传输，需要传输156 Byte，采用垂距法需要传首尾两个点，第1 个点迹传输批号、录取时间、坐标、高度信息，大小为11 Byte，第2 个点传输最后一个点，传输批号、录取时间、坐标、高度、这一段点的个数信息，大小为13 Byte，总共需要传输24 Byte，压缩率达到84.6%。采用分裂法和分段直线拟合法进行压缩需要传输3 个点和每段的个数，第1 个点迹传输批号、录取时间、坐标、高度信息，大小为11 Byte，第2 个点传输分段点第6 个点，传输坐标、高度和这一段的个数6，个数占用1 Byte，总共需要9 Byte，第3 个点传输最后一个点传输批号、录取时间、坐标、高度、这一段点的个数信息，大小为12 Byte，总共需要传输32 Byte，压缩率达到79.4%。二阶多项式拟合需要传输首尾两个点和曲线的5 个参数，总共需要33 Byte，压缩率为78.8%。不同算法的压缩率如表4 所示。

表3 算法误差与分段直线拟合误差之比

表4 算法的压缩率

虽然垂距法的压缩率最高，但是该算法的误差太大，已经不能表示原始的航迹情况，综合运算量、误差和压缩率比较，分段直线拟合是最佳的航迹压缩算法。

3 结论

雷达是获取战场信息的主要方式，将雷达获取的空情信息传输到指挥所进行统一处理，是指挥员掌握战场综合态势，正确判断和决策的重要基础，在战争中起到决定性的作用。战场就是双方相互对抗的一个过程，雷达的通信一旦遭到干扰和破坏，我方将处于极大的劣势状态。北斗短报文是一种稳定、可靠的通信方式，但是其通信带宽有限，无法满足大数据量的雷达通信。本文提出的压缩算法简单、运算量小，对硬件处理器的要求较低，易于编程实现，并且压缩效果好，在一定误差范围内，能够满足有限带宽条件下应急空情传输的需要，该算法还可应用于船舶航迹、远程控制等数据的压缩，具有很好的应用前景。