改进MUSIC 算法超音速空速估计*
郑春梅,王文军
(1.忻州职业技术学院,山西 忻州 034000;2.华北理工大学矿业工程学院,河北 唐山 063210)
0 引言
航空业的快速发展,使得传统空速管测量方法不能满足超音速时代各种高速、高机动飞行器的空速测量需求,超声速环境要求非探出的大气数据传感装置以适应因摩擦而产生的高热环境,而隐身飞机低雷达反射面需求,也提出新的要求。为此,上世纪开始,国内外相继展开这方面的研究,美国FADS[1]在精度和可靠性方面展现出强大优势,其依靠嵌入在飞行器前端的压力传感器阵列来测量压力分布,以此间接获得飞行参数[2]。但FADS 系统算法运算复杂、迭代存在发散及需要大量前期数据,动静压测量模型是非线性的,且某些系数需风洞试验标定,限制了系统的实用性。
声矢量传感器由相互垂直放置的质点振速传感器及压力传感器组成,可同步测量声压和振速[3],比广泛用于声速测量但仅感受声压信息的传统声传感器,可以获得更多的信息量。为此朱维庆等[4]利用声传感器提出了一个测量低空飞行飞机的速度和髙度方法;Cevher 等[5]研究了测量流体速度的声相关测速理论;陈诚等[6]的鲁棒H∞滤波空速估计算法,在分析声场质点振速与空气流速度关系基础上,建立声矢量传感器阵列空速测量模型,利用通过多个传感器测量结果之间的数学迭代来提高空速测量的精度,但运算量较大,且数据的统计特性不明显;虞飞等[7-8]提出基于MUSIC 算法的近场空速估计,借助有效声速概念,建立声矢量传感器阵列在稳定气流作用下的近场输出模型。
已有算法在亚音速范围内取得较好的估计结果[9],但对于超音速条件下形成的马赫锥特性,估计精度不足[10]。为此,本文针对超音速气流中声波的传播模型展开研究,基于声矢量传感器的测量模型并结合MUSIC 算法[11],提出了基于时空扩展改进MUSIC 算法的超音速空速估计方法,并针对算法计算量大的特点[12],给出了快速算法,实验验证了算法的有效性。
1 阵列输出模型
设3 质点声矢量传感器在空间同一点处正交放置,同时测量位于正交方向的质点振速,测量装置为内径为D 的圆柱型管路,剖面示意图如图1所示。
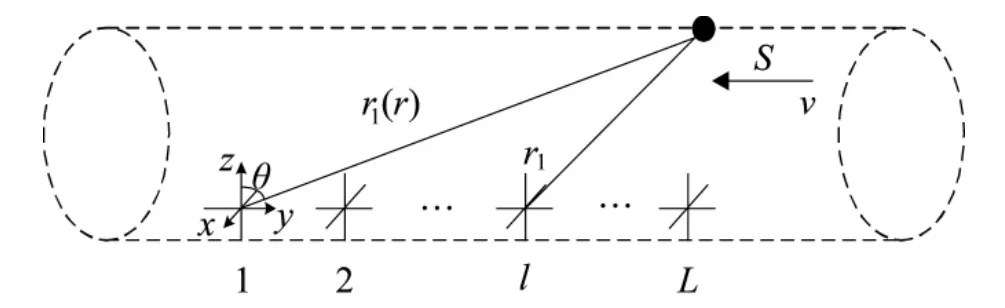
图1 声矢量传感器阵列测量模型
则单个声矢量传感器的近场阵列流型为[7]:
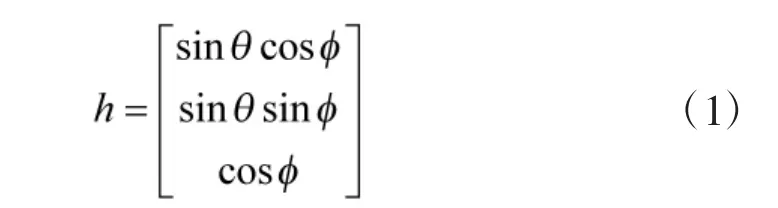


式中,aM为包含待估空速的阵列流形矢量,s(t)为参考阵元的接收信号,则整个阵列的输出信号为:
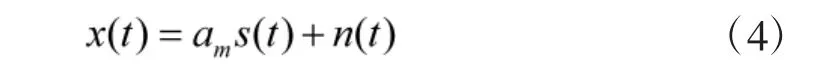
式中,n(t)为分量相互独立的加性高斯白噪声矢量。
2 声波在超音速稳定气流中的模型构建
声波在均匀、恒温、无粘性的流动空气中传播时,满足如下线性方程和波动方程[11],

式中,ρ 为空气密度,p 为质点声压,V 为质点振速,Δ为梯度运算,Δg表示向量的散度运算,v·Δ表示无向算子。当空速为0 或‖v‖<c 时,声波传播模型见文献[7],而当‖v‖>c,即空速进入超音速时,声波在传播过程中形成如图2 所示马赫锥,图中各波阵面和马赫锥边缘相切,形成等效声源。
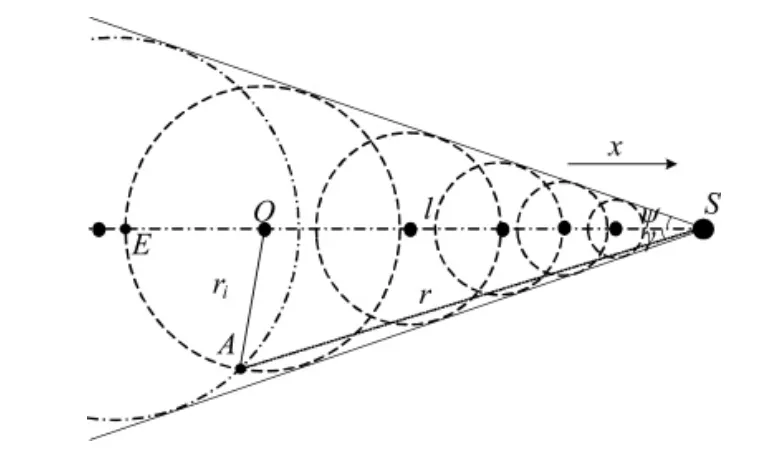
图2 马赫锥内波阵面分布
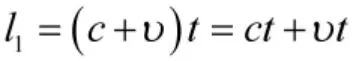

式(7)为关于ri的一元二次方程,对于超音速气流有M>1,则由根判别式可得:

对于式(8),当Δ=0 时有一对重根,即仅一个波阵面作用于A 点,此时A 位于锥边缘区域。而当Δ>0 时有两个不等的根,即有两个波阵面叠加作用于A 点,此时A 点位于锥内,其振速由两个波阵面等效声源和叠加,等效声源的等效半径为:
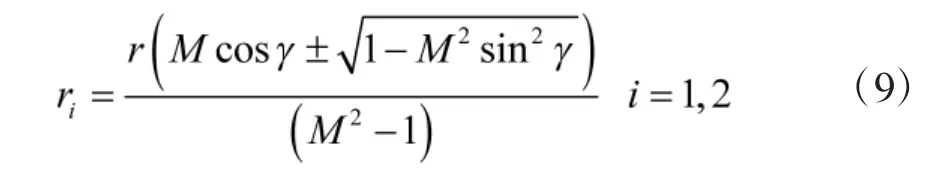
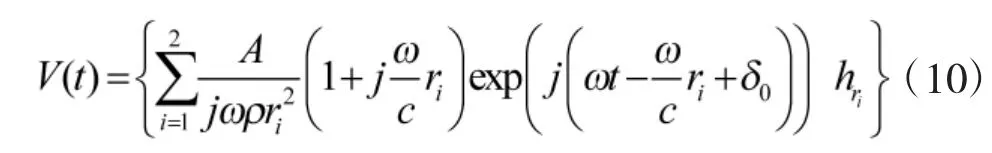
3 改进MUSI 算法超音速空速估计
3.1 改进MUSI 算法空速估计
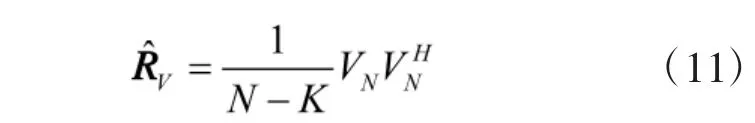

图3 矢量传感器测量原理图

对于超音速气流,MUSIC 谱峰值所对应的υ,就是空气流动速度的估计值,

3.2 空速估计快速算法
基于时空扩展改进MUSIC 算法的空速估计算法需要在整个超音速域进行搜索,运算量较大,为此提出快速算法,以较少的精度损失获得更强的空速估计实时性。
由子空间原理可得,阵列流形矢量aM与信号子空间us所形成空间同为信号子空间,则结合式(3)通过us可以得出阵列流形矢量aM的估计值为
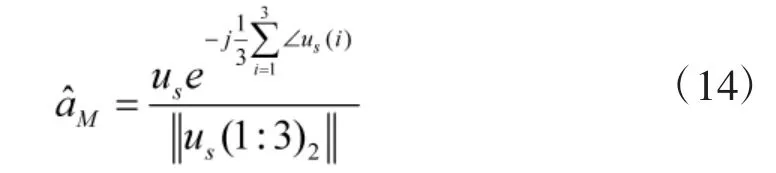


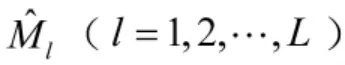
4 仿真实验

4.1 速度估计的伪谱
如图4 所示为在不同超音速条件下,空速MUSIC 估计的谱峰图,从图中可以看出,在真实的空速处形成了谱峰,根据谱峰的位置,可以估计出气流速度。
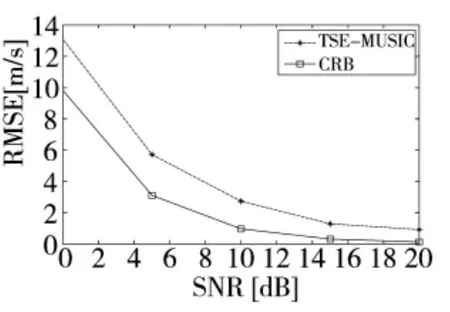
图5 空速估计的RMSE随信噪比的变化曲线
4.2 算法的统计性能
4.2.1 信噪比对估计的影响
图5 给出了空速估计的均方根误差(RMSE)随信噪比的变化曲线。可以看出,随着信噪比的增大,空速估计的RMSE 是逐渐减小的,说明算法估计精度越来越高。所提算法的RMSE 与估计的CRB 相差不多,说明估计误差的方差接近于最小值。
4.2.2 快拍数对估计的影响
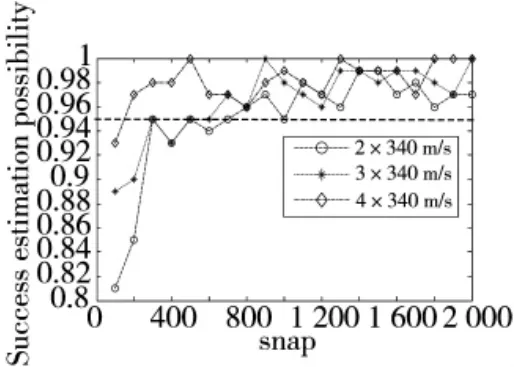
图6 空速估计成功概率随快拍数的变化曲线
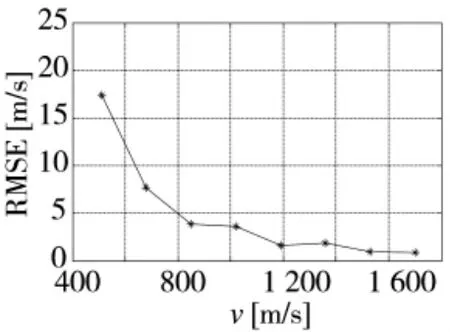
图7 空速估计RMSE 随空速的变化曲线
如图6 所示为不同中超音速下,空速估计成功(估计误差|Δυˆ|≤0.01υ)概率随快拍数的变化曲线,可以看出,随着快拍数的增加,估计成功的概率逐渐收敛。当快拍数大于700 时,空速估计的成功概率达到95%以上,这说明空速估计都是可信的。
4.2.3 空速对估计的影响
如图7 所示为空速从1.5c 变化至5c 时,空速估计的误差随变化曲线,可以看出,估计精度随着空气速度的增加而增加。当空速较小时,两个等效声源的半径相差较大,故估计误差相对较大。但是在测量区间内,估计误差均在可接受的范围之内。
5 结论
针对超音速马赫锥特点,分析出锥内任何一点有且仅有两个波阵面相叠加,且波阵面可被认为是由等效声源产生,基于此利用声矢量传感器的测量模型,提出了基于时空扩展改进MUSIC 算法的超音速空速估计算法,并针对算法运算量大的特点给出算法快速实现。实验结果表明,所提算法能够准确地估计超音速空气流动速度,快速算法在损失较少精度情况下极大地提高算法的实时性。

