三维线性相位FIR数字滤波器对称特性的设计

文/殷仕淑 武岳 常郝

1 引言

对多维信号处理的研究工作最早可以追溯到上世纪60年代。D.P. Petersen 与D. Middleton在文献[1]中首次开展了对多维频带有限信号进行抽样和重建工作的理论研究。此后，在多维数字滤波器的研究领域里，致力于二维数字滤波器理论及设计方法的研究工作占据绝大部分分量，发展很快。相较而言，由于数据量大，系统复杂度增加，处理三维空间信号（例如三维医学影像信号，地球物理空间信号等）的三维数字滤波器（Three dimensional digital filters: 3D DF）的相关理论及设计工作进展不大。设计一个长度为10的FIR一维数字滤波器，最多有10个未知变量待求。设计一个三维长度都为10的FIR三维数字滤波器，待求的未知变量数为1000。虽然滤波器的设计问题描述相同，但庞大的未知变量数对于算法的有效收敛是个极大考验。虽然可以利用低维滤波器去处理三维信号，但考虑到数据之间的相关性，尤其是在移动图像处理、机器视觉、医学图像处理、地震信号处理和其他地球物理等三维空间信号处理领域中，发展三维数字滤波器的概念和研究三维数字滤波器的设计问题仍旧是不可避免的。

本文主要讨论线性相位三维FIR数字滤波器的分类和设计工作。与IIR滤波器相比，FIR系统的单位脉冲长度有限，满足绝对可和系统稳定性判断条件。其次，FIR数字滤波器可以实现线性相位响应。最初FIR三维数字滤波器的设计是以一维数字滤波器为原型，采用McClellan变换(McClellan transform)进行转换得到的[2-7]。遗憾的是，这种方法无法精确控制三维数字滤波器的频率特性。优化迭代算法是另一种比较常见的用来设计FIR 三维数字滤波器方法。滤波器的设计问题写成线性规划问题求解，且不用约束其系统稳定性[8,9]。在文献[10,11]中，解析最小二乘法用来求解FIR三维数字滤波器。为了降低设计工作的计算复杂度，FIR三维数字滤波器的设计工作充分利用三维空间的对称特性[4,5,8-13]。即便如此，在上述文献中所获得的FIR三维数字滤波器频谱特性仍旧不太令人满意。此外还有一些工作尝试采用比较新颖的算法思想来解决FIR多维数字滤波器的设计问题，如模拟退火算法[14]，凸集投影法[15]，但遗憾的是三维数字滤波器的实验数据并没有被成功获取。

研究三维数字滤波器的对称特性可以从频域（幅度响应，相位响应）和空域（或称时域，即系统单位脉冲响应或滤波器系数）两个方面入手，如：球面对称和立方对称等属于频域概念[16-18]。基于平面对称概念所定义的多种不同幅度响应对称特性以列表的形式报告于[19]。在文献[8]中，作者对滤波器的幅度平方响应对称性进行研究，得出三维数字滤波器的幅度平方响应共有47种不同类型对称性。而在文献[11]中，基于单位脉冲响应三维数据的长度奇偶性和对称奇偶性的不同组合，得出共有64种不同类型的线性相位FIR三维数字滤波器类型。类似地，在1998年，线性相位一维数字滤波器单位脉冲响应对称性的四种组合被移植至多维系统[20]。本文中，在文献[11,20]工作的基础上，拟对单位脉冲响应三维数据对称性的64种组合进行分析，剔除冗余数，初步提出20种不同类型的线性相位FIR三维数字滤波器。结合零点位置分析，给出设计不同种类（低通、高通、带通和带阻）线性相位FIR三维数字滤波器的单位脉冲响应对称特性的选取。为了得到线性相位三维FIR数字滤波器，本文把此类型滤波器的设计问题写出凸问题，采用约束凸规划进行求解[21]，获得具有良好频率特性的线性相位三维FIR数字滤波器。最后给出设计实例。

2 3D FIR线性相位数字滤波器

对于一个因果的FIR三维数字滤波器，其单位脉冲响应可以用三维矩阵数据来表示：其系统函数表示为：

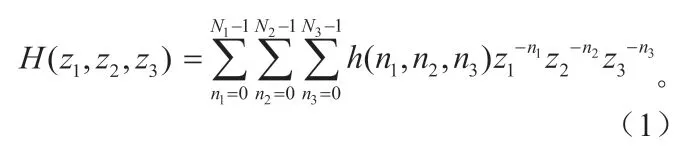
系统的频率响应定义为滤波器单位脉冲响应的离散时间傅里叶变换（Discrete-time Fourier transform: DTFT），是式（1）中z变量在z平面单位圆上取值，即，

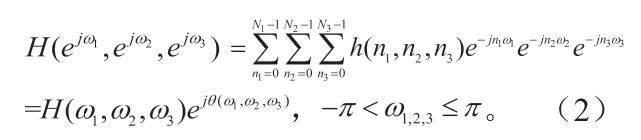
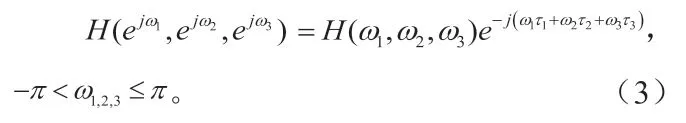
类似于一维数字滤波器单位脉冲响应的对称性分析， FIR三维数字滤波器在三维方向滤波器长度在每一维度方向上可能是奇数长度也可能是偶数长度，且在每一维度方向可能是奇对称，也可能是偶对称的。因此，FIR三维数字滤波器的单位脉冲响应每一维度方向有四种可能组合：

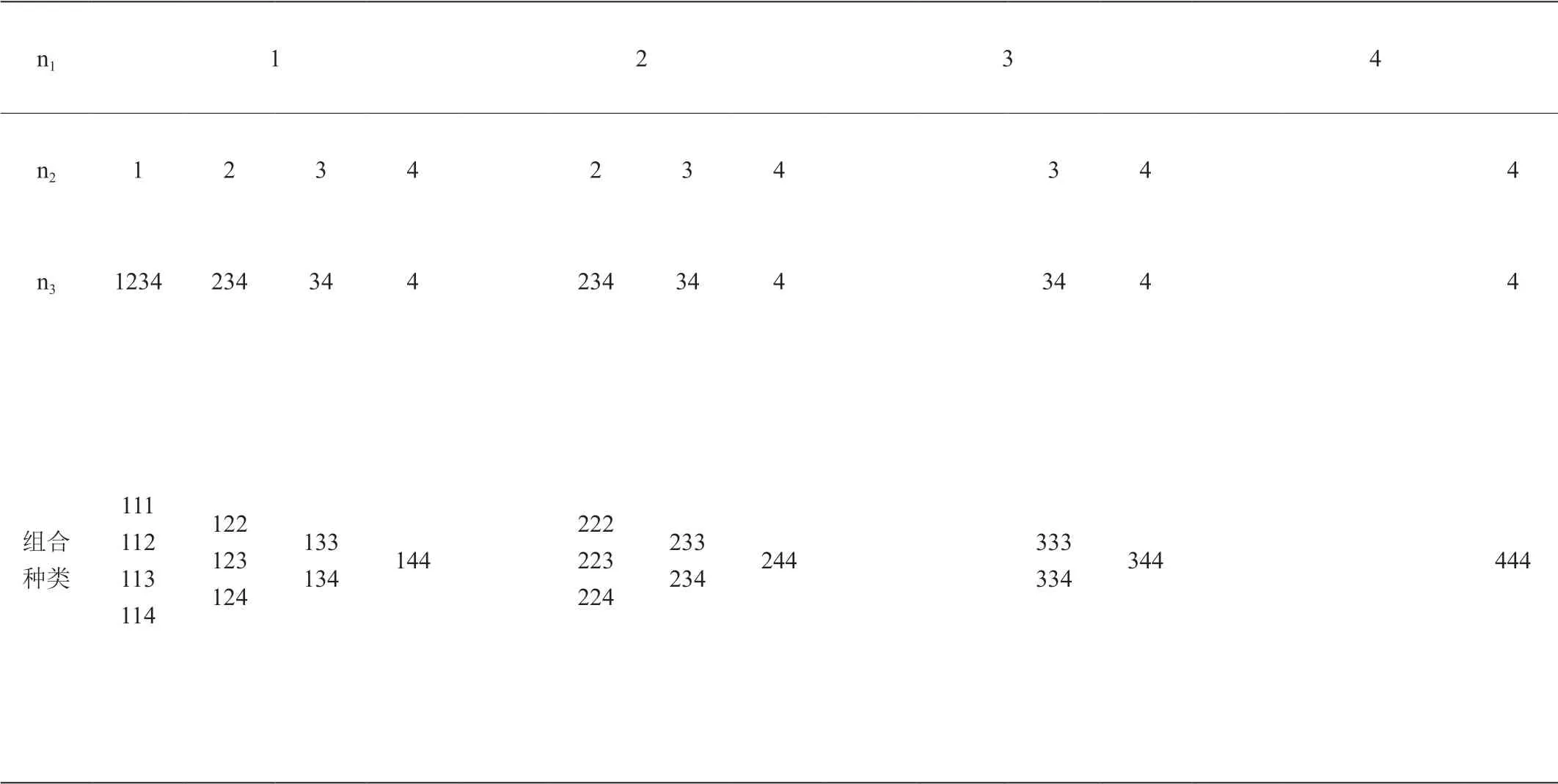
表1：单位脉冲响应三维方向对称特性组合种类

（1）长度为奇数且偶对称；

（2）长度为偶数且偶对称；

（3）长度为奇数且奇对称；

（4）长度为偶数且奇对称。

也就是文献[11]中所说的一共有64种组合。我们可以用数组（111），（112），（121），。。。，（444）来表示这64种组合。

利用线性相位滤波器单位脉冲响应的数据对称性，我们可以很方便地写出表1中三维FIR线性相位滤波器的频率响应。例如，现有某FIR三维数字滤波器的单位脉冲响应三维方向对称特性为表1中组合“111”，则有：

其中，

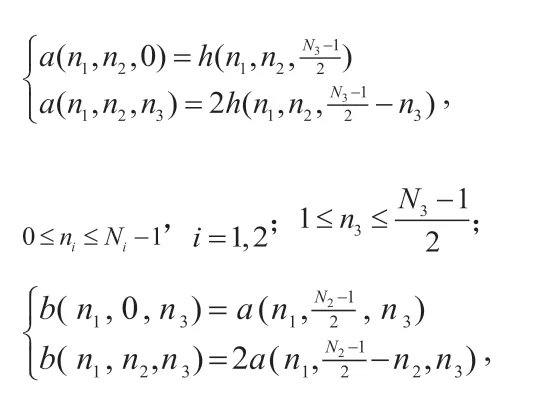
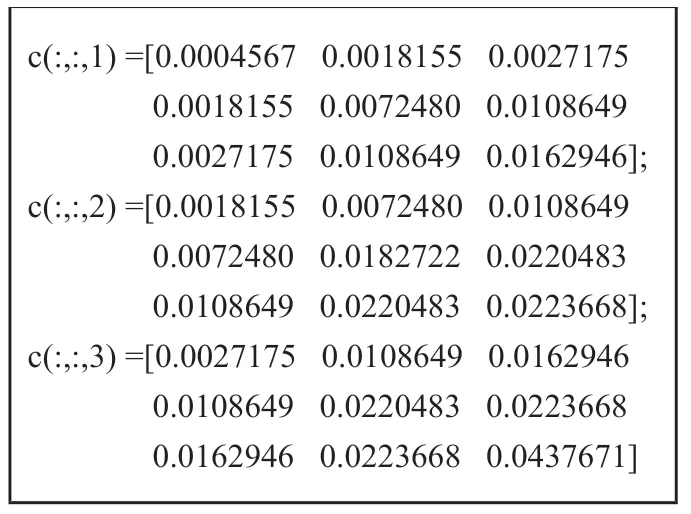
表2：例1中三维线性相位FIR滤波器系数

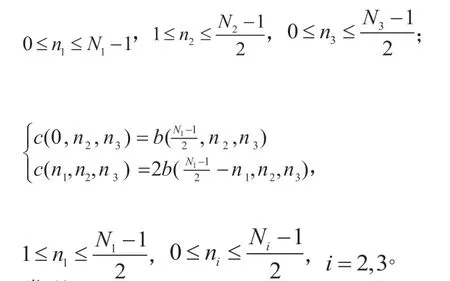
发现：

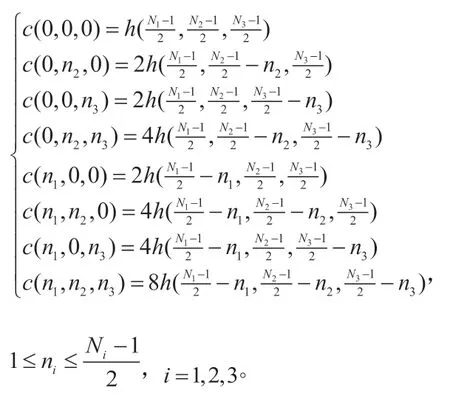
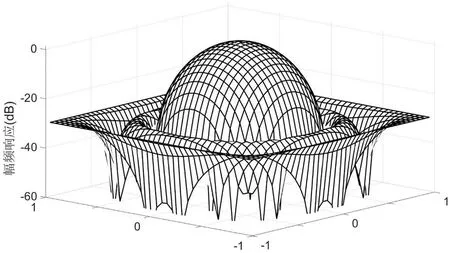
图1：三维FIR数字滤波器幅频特性

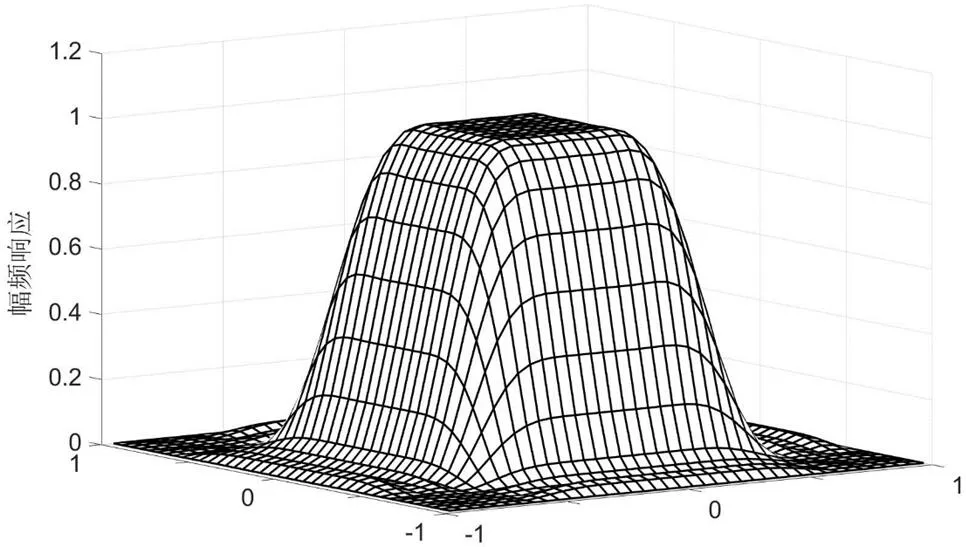
图2

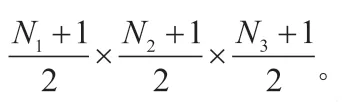
再例如：对于组合（444），利用滤波器系数对称特性，滤波器的频率响应可以写成：

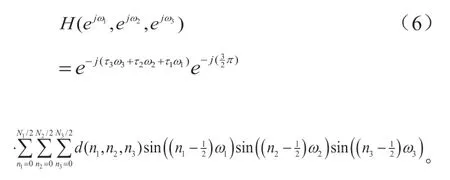
其中，

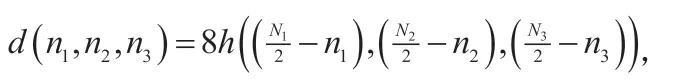
对于一维线性相位FIR滤波器的四种类型，类型1可用于设计低通（LP），带通（BP），高通（HP），和带阻（BS）滤波器；类型2可用于设计LP和BP滤波器；类型3仅能用于设计BP滤波器；类型4可用于设计HP和BP滤波器。因此，表1中20种类型中适用于设计在三个维度里具有相同通阻特性的线性相位FIR滤波器为：低通（111，112，122，222）、带通（全部组合）、高通（111，114，144，444）和带阻（111）。如果滤波器的三个维度具有不同的通阻特性，则根据具体要求可选择不同组合种类。

在接下来的小节，我们把三维线性相位FIR滤波器组的设计问题写出极小化极大值问题，带入约束凸规划求解。

3 线性相位3D FIR数字滤波器的设计

基于CVX工具箱的约束凸规划法（DCP），用来求解各类凸问题[21]。与半定规划（SDP）法和二阶锥规划（SOCP）法相比，DCP对问题描述简单直观，求解复杂问题的能力更强。为了采用CVX求解三维线性相位FIR数字滤波器的设计问题，我们先把FIR三维数字滤波器的设计问题表达成极小化极大值问题：

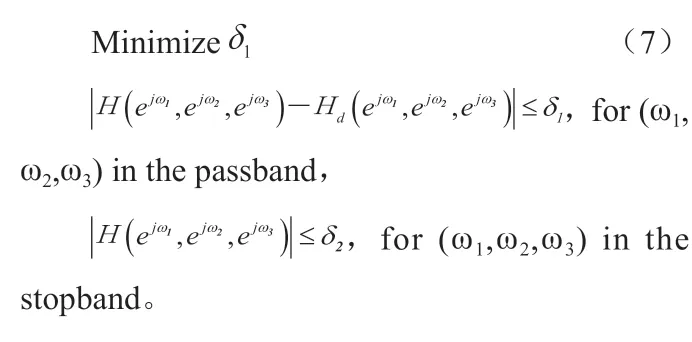
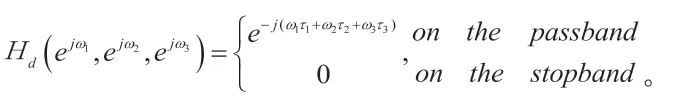
采用DCP设计FIR一维或二维数字滤波器时，问题描述相同。唯一不同的是在（7）式中待求未知变量数是三维变量。在滤波器每维度系数长度一样时FIR三维数字滤波器的待求变量是一维数字滤波器的倍。式（7）可以用来求任意相位响应的FIR滤波器。对于线性相位FIR滤波器，可以利用其滤波器系数的对称性，来降低待求变量数。只是对于表1中的不同组合形式，式5要做不同的改写。例如组合111，式（7）改写如下：

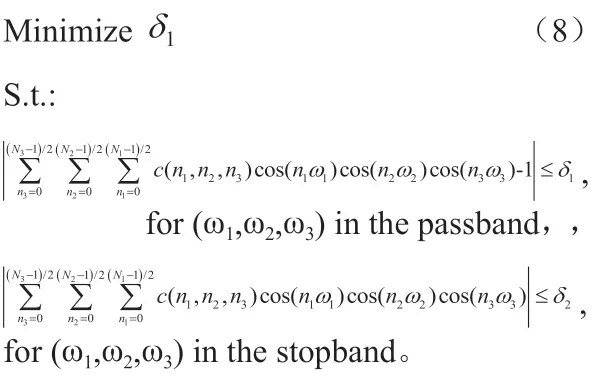
4 三维线性相位FIR数字滤波器的设计实例

设计三维线性相位FIR数字滤波器时，必须预先了解以下几点：

（1）所期望的滤波器单位脉冲响应长度；

（2）所期望的滤波器分段频率特性（低通、高通等）及截止频率点；

（3）所期望的滤波器通带/阻带形状（球形、立方形等）；

（4）所期望的滤波器通带或阻带所能接受的最大波纹误差。

一般来说，滤波器系数的长度、过渡带宽度（通带与阻带之间的间隔）和通带、阻带上的波纹误差之间是一种相互制衡的关系。滤波器系数越长，过渡带越宽，则通带和阻带波纹误差则越小。而通带和阻带波纹误差之间也有相互制衡的关系，压缩通带的波纹误差，也就是要获得更好的通带平坦性，则在其他参数不变的前提下，必然以增大阻带波纹误差作为代价。

例1：设计一个长度(5，5，5)，球面对称，线性相位的低通FIR三维数字滤波器。通带截止频率和阻带截止频率分别为（0.3π，0.6π），滤波器的阻带最大波纹误差设为-30dB。把滤波器设计问题写成式（8）进行求解。待求系数c(n1,n2,n3)大小为（3×3×3）个。图1中显示其幅度频率响应。

由于所得滤波器在三个维度方向上具有对称性，从另外两个维度看进去的滤波器幅频特性与图1中是一致的。其滤波器系数列于表2中，以供读者参考。仔细观察表2中数据，可发现每页数据具有关于对角线对称的特性；并且第一页第二列数据与第二页第一列数据相同，以此类推。表2中滤波器系数的对称性缘于本例中所要求设计的滤波器在三个维度上通阻带截止频率点相同，滤波器长度一致，即滤波器在幅频上具有对称性。这种幅频对称特性也可以用来降低滤波器设计过程的未知变量数。但这种幅频对称特性在单位脉冲响应上的影响较为复杂，尤其是滤波器比较长的时候。例2：设计一个长度(12，12，12)，通带区域方形对称，线性相位的低通FIR三维数字滤波器。通带截止频率和阻带截止频率分别为（0.3π，0.6π），滤波器的阻带最大波纹误差设为-30dB。待求系数c(n1,n2,n3)大小为63个。图2显示的是所得三维FIR数字滤波器幅频响应图，其在通带的最大波纹误差为2.048e-3。由于篇幅所限，滤波器系数没有列出来。

5 结束语

在处理三维数字信号时，考虑到数据之间的相关性，三维数字滤波器的设计不可避免。三维数字滤波器设计工作的难点在于庞大的待求未知变量数。本文从一维线性相位FIR滤波器系数的对称性出发，首次提出三维线性相位FIR滤波器共有20种不同类型。利用滤波器系数的对称性，大幅度减少滤波器设计过程中待求未知变量淑，把三维线性相位FIR数字滤波器的设计问题写成极大值极小化问题，带入凸规划求解。实验结果显示，这种方法可以获得具有良好频率特性的三维线性相位FIR滤波器。