基于Dijkstra算法的旅游路线规划研究

吴昕宇　罗雪颖

摘要：考虑游客不会在游览路线上往返、游览路线不会重复，基于此，本文采用Dijkstra算法解决这个问题。首先，运用图论知识，将8个景点（包括景石）看成一个赋权无向图，各景点为图的顶点，两景点之间步行最短路线为图相应两顶点问的边，距离为图两顶点问边的权值，得到赋权图。然后，用Dijkstra算法即可求解最短路线。

关键词：Dijkstra算法图论知识最短路线

引言

在物质生活条件得到极大发展的今天，人们越来越追求精神文明的建设，越来越多的人爱上旅行而背上背包去旅行。这就致使旅游资源供不应求，一到假期便游人如织，在这样的情况下，规划游客的最优路线，规划游客的观光时间，最大限度地利用旅游资源便十分重要。

2010年，江苏省启动潘安湖土地整理项目，在一片废墟上建成了一个6500亩湖面的国家级水利风景区。2016年，贾汪被列为“国家全域旅游示范区”首批创建单位。本文选取潘安湖景区的部分景点，完成徐州潘安湖风景区游览最短路线设计问题。

1模型建立

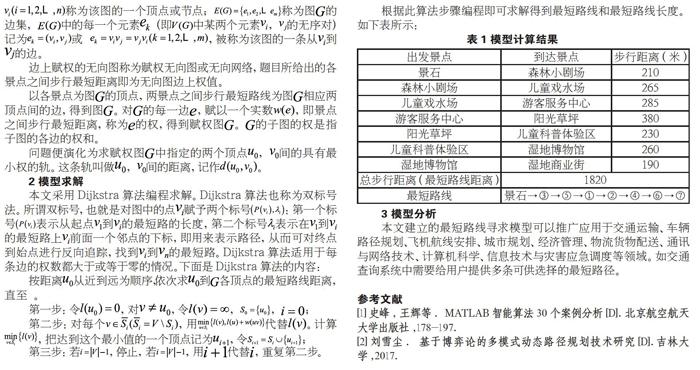
从景石出发步行游览①游客服务中心，②阳光草坪，③森林小剧场，④儿童科普体验区，⑤儿童戏水场，⑥湿地博物馆，⑦湿地商业街。建立数学模型，找出所有景点至少观光1次的距离最短的路线，计算该路线的长度。

本问题要求设计从景石出发，经过①②③④⑤⑥各景点，最终到达⑦湿地商业街，① ⑥所有景点至少观光1次的距离最短的路线。在实际旅游观光中，游客在各景点的旅游路线不会重复，而且游客不会在旅游路线上往返，基于此，本文将采用Dijkstra算法来解决此问题。

2.1无向图定义

一个无向图G是由一个非空有限集合V（G）和V（G）中某些元素的无序对集合E（G）构成的二元组，记为G=（v（G），E（G））。其中，V（G）={v1，v2，L，v，）称为图G的顶点集或节点集，V（G）中的每一个元素

边上赋权的无向图称为赋权无向图或无向网络，题目所给出的各景点之间步行最短距离即为无向图边上权值。

以各景点为图G的顶点，两景点之间步行最短路线为图G相应两顶点间的边，得到图G。对G的每一边e，赋以一个实数w（e），即景点之间步行最短距离，称为e的权，得到赋权图G。G的子图的权是指子图的各边的权和。

问题便演化为求赋权图G中指定的两个顶点uo，vo间的具有最小权的轨。这条轨叫做uo，vo间的距离，记作d（uo，vo）。

2模型求解

本文采用Dijkstra算法编程求解。Dijkstra算法也稱为双标号法。所谓双标号，也就是对图中的点vf赋予两个标号（，（u），1）：第一个标号（p（v1）表示从起点V1到V1的最短路的长度，第二个标号λ3表示在v1到v1的最短路上V1前面一个邻点的下标，即用来表示路径，从而可对终点到始点进行反向追踪，找到U1到vn的最短路。Dijkstra算法适用于每条边的权数都大于或等于零的情况。下面是Dijkstra算法的内容：

按距离uo从近到远为顺序，依次求uo到G各顶点的最短路线距离，直至。

3模型分析

本文建立的最短路线寻求模型可以推广应用于交通运输、车辆路径规划、飞机航线安排、城市规划、经济管理、物流货物配送、通讯与网络技术、计算机科学、信息技术与灾害应急调度等领域。如交通查询系统中需要给用户提供多条可供选择的最短路径。

参考文献

[1]史峰，王辉等.MATLAB智能算法30个案例分析[D].北京航空航天大学出版社，178-197.

[2]刘雪尘，基于博弈论的多模式动态路径规划技术研究[D]，吉林大学，2017.