关于BCH-代数原子与分支的一些结果

李金龙

(陕西理工大学 数学与计算机科学学院,陕西 汉中 723000)

文献[1]提出了BCI-代数的概念.若〈X;*,0〉是一个BCI-代数,在X上定义一个二元关系

≤:x≤y⟺x*y=0,

则“≤”为X上的一个偏序关系.文献[2]提出了BCH-代数.众所周知,BCI-代数类是BCH-代数类的真子类,因此对BCH-代数的研究就更加困难一些,但通过研究所得到的结果却更具有普遍性.在一般的BCH-代数中，上述的二元关系不是一个偏序关系,为了把BCI-代数中的偏序关系推广到BCH-代数中，文献[3]提出了偏序BCH-代数的概念.文献[4]在BCH-代数中引入了原子与分支的概念.作者将主要研究一般的BCH-代数和偏序BCH-代数的原子与分支的一些性质.

1 预备知识

为行文方便,先引入下面的一些定义和引理,同时给出引理中的两个推论.

定义1[2]一个(2,0)型代数〈X;*,0〉叫做BCH-代数,如果∀x,y,z∈X,它满足下列公理：

H-1x*x=0;

H-2x*y=y*x=0 ⟹x=y;

H-3 (x*y)*z=(x*z)*y.

定义2[3]设〈X;*,0〉是一个BCH-代数,若x≤y,x*y=0,且∀z∈X,有z*y≤z*x,则称〈X;*,0〉是一个偏序BCH-代数.

定义3[4]设〈X;*,0〉是一个BCH-代数,元素a∈X,若x∈X,x*a=0,即x≤a,则x=a,称元素a为〈X;*,0〉的一个原子.

文献[4]指出,元素0是BCH-代数〈X;*,0〉的一个原子,以L(X)记BCH-代数〈X;*,0〉中所有原子的集合,即L(X)={a∈X:若x∈X,x*a=0,则x=a},则0∈L(X),故L(X)≠∅.

定义4[4]设〈X;*,0〉是一个BCH-代数,a∈L(X), 记V(a)={x∈X:a*x=0即a≤x},称V(a)为〈X;*,0〉的一个分支.

定义5[5-7]设〈X;*,0〉是一个BCH-代数,X的一个非空子集A被称为一个理想,如果它满足:

(1) 0∈A;

(2)x*y∈A,y∈A⟹x∈A.

定义6[8-12]设〈X;*,0〉是一个BCH-代数,若∀x∈X,有0*(0*x)=0*x(等价于(0*x)*x=0),则称〈X;*,0〉是一个拟结合BCH-代数.

引理1[4]设〈X;*,0〉是一个BCH-代数,x∈X,∀y∈X,下列条件等价：

(1)x∈L(X)；

(2) 0*(0*x)=x；

(3)y*(y*x)=x.

引理3[4-5]设〈X;*,0〉是一个BCH-代数,则∀x,y∈X,有下列结论成立：

(1) [x*(x*y)]*y=0;

(2)x*0=x;

(3) 0*(x*y)=(0*x)*(0*y);

(4) 0*[0*(0*x)]=0*x.

引理4[3]设〈X;*,0〉是一个偏序BCH-代数,则X中的二元关系≤是一个偏序关系.

引理5[4]设〈X;*,0〉是一个BCH-代数,若a,b∈L(X),则∀x∈V(a),∀y∈V(b),恒有x*y∈V(a*b).

特别指出,若取a=b,由H-1,得a*a=0,故有下面的推论1.

推论1设〈X;*,0〉是一个BCH-代数,若a∈L(X),则∀x,y∈V(a),恒有x*y∈V(0).

引理6[6]设〈X;*,0〉是一个BCH-代数,则∀x,y∈X,有

[0*(x*y)]*(y*x)=0,x*y∈B(X)⟺y*x∈B(X).

引理7[4]设〈X;*,0〉是一个BCH-代数,则L(X)是一个广义结合BCI-代数.

引理8[4]设〈X;*,0〉是一个BCH-代数,若a,b∈L(X),且a≠b,则V(a)∩V(b)=∅.

根据引理5,若a,b∈L(X),则∀x∈V(a),∀y∈V(b),恒有x*y∈V(a*b),因a与b都是原子,故当a≠b时,有a*b≠0.由引理7,知a*b∈L(X),即a*b是X的原子,再由引理8,得V(a*b)∩V(0)=∅,所以x*y∉V(0).

推论2设〈X;*,0〉是一个BCH-代数,若a,b∈L(X),且a≠b,则∀x∈V(a),∀y∈V(b),恒有x*y∉V(0).

引理9[5]设〈X;*,0〉是一个BCH-代数,Y是X的一个非空子集,则Y是X的子代数的充要条件是Y对运算*封闭.

引理10[4]设〈X;*,0〉是一个BCH-代数,∀x∈L(X),∀y∈X,则x*y∈L(X).特别地,0*y∈L(X).

引理11[7]设〈X;*,0〉是一个BCH-代数,令B(X)={x∈X:0*x=0},则B(X)是X的一个子代数,也是X的一个理想.

由定义4，知B(X)=V(0).

引理12[12]设〈X;*,0〉是一个BCI-代数,x,y∈X,若x≤y,则∀z∈X,有z*x≤z*y,x*z≤y*z.

引理13[5]设〈X;*,0〉是一个BCH-代数, 若∀x,y,z∈X,有[(x*y)*(x*z)]*(z*y)=0成立，则〈X;*,0〉是一个BCI-代数.

2 主要结果

下面给出一般的BCH-代数和偏序BCH-代数中原子与分支的一些性质,最后给出一个BCH-代数的BCI-化定理.

定理1设〈X;*,0〉是一个BCH-代数,a∈L(X),则∀x∈V(a),有0*(0*x)=a,称0*(0*x)为元素x的广义结合乘积.

证明因x∈V(a),故a*x=0.由H-3和H-1,得0*a=(a*x)*a=(a*a)*x=0*x,从而有0*x=0*a.两端左乘0,得0*(0*x)=0*(0*a).由引理1,得0*(0*a)=a,有0*(0*x)=a.

定理1在后面一些定理的证明中起着关键性的作用.由引理2知,∀x∈X,∃a∈L(X),使x∈V(a).结合定理1知,一个BCH-代数中任一元素的广义结合乘积等于它所在分支中的原子,这样就把BCH-代数中的任一元素与它所在分支中的原子紧密地联系起来了,也说明了原子这一概念在BCH-代数中起着非常重要的作用.

定理2设〈X;*,0〉是一个BCH-代数,a∈L(X),x∈V(a),y∈X,若y≤x，即y*x=0,则y∈V(a).

证明因为y*x=0,由H-3和H-1,得

0*y=(y*x)*y=(y*y)*x=0*x,

故0*y=0*x,两端左乘0并利用定理1，得0*(0*y)=a.两端右乘y并利用引理3的(1),得a*y=0,所以y∈V(a).

由引理4知,若〈X;*,0〉是一个偏序BCH-代数,则是一个偏序集.因为一般只有在偏序集中才有极小元的概念.根据极小元与原子的定义,偏序BCH-代数中的原子正好就是在偏序关系≤下的极小元，故称偏序BCH-代数的原子为极小元.

定理3设〈X;*,0〉是一个偏序BCH-代数,a是X的一个极小元,有

(1)a*V(0)={a*x:x∈V(0)}={a};

(2) 若x∈X,且0≤x*a,有x∈V(a);

(3)x∈V(a)的充要条件是x*a∈V(0).

证明(1) ∀x∈V(0),则0≤x,由偏序性和引理3的(2)，得a*x≤a*0=a,因a是X的一个极小元,故a*x=a,即证明了a*V(0)={a}.

(2) 因0≤x*a,由偏序性和引理3的(2)，得x*(x*a)≤x*0=x.又因a是X的一个极小元,再由引理1，得x*(x*a)=a,所以a≤x,即x∈V(a).

(3) 必要性由推论1可得,充分性由定理3的(2)可得.

定义7设〈X;*,0〉是一个BCH-代数,A与B是X的两个非空子集,称A*B={x*y:x∈A,y∈B}为A与B的乘积.

定理4设〈X;*,0〉是一个偏序BCH-代数,a是X的一个极小元,m是X的非空子集A的最大元,则a*m是V(a)*A中的最小元.

证明因为m是X的非空子集A的最大元,故∀x∈A,有x≤m,由偏序性，得a*m≤a*x.又∀y∈V(a),由定理1，得0*(0*y)=a,再由H-3,引理3的(3)和引理6，得

(a*x)*(y*x)={[0*(0*y)]*x}*(y*x)=

[(0*x)*(0*y)]*(y*x)=[0*(x*y)]*(y*x)=0,

因此a*x≤y*x.最后由引理4，得a*m≤y*x.显然a*m∈V(a)*A,即证明了a*m是V(a)*A中的最小元.

定理5设〈X;*,0〉是一个偏序BCH-代数,a是X的一个非0极小元,则V(0)∪V(a)是X的一个子代数的充要条件是∀x∈V(a),a≤0*x.

证明必要性. 设V(0)∪V(a)是X中的一个子代数,∀x∈V(a),因0∈V(0),有0*x∈V(0)∪V(a).又因a≠0,由推论2，知0*x∉V(0)，有0*x∈V(a),所以a≤0*x.

充分性.为证V(0)∪V(a)是X中的一个子代数,由引理9知,只需证明∀x,y∈V(0)∪V(a),V(0)∪V(a)对运算*是封闭的即可.为此，分以下几个情形.

情形1设x,y∈V(0),或x,y∈V(a).由推论1，知x*y∈V(0)⊆V(0)∪V(a).

情形2设x∈V(0),y∈V(a).下面证明x*y,y*x∈V(a)⊆V(0)∪V(a).

因x∈V(0),故0≤x,由偏序性和引理3的(2)，得y*x≤y*0=y∈V(a),再由定理2，知y*x∈V(a).

又因x∈V(0),故0*x=0,由H-3和引理3的(3)与(1)，得

(0*y)*(x*y)=[0*(x*y)]*y=[(0*x)*(0*y)]*y=[0*(0*y)]*y=0,

因此0*y≤x*y.又由已知条件，知a≤0*y;最后由引理4，得a≤x*y,所以x*y∈V(a).

定理6设〈X;*,0〉是一个偏序BCH-代数,a是X的一个极小元,x,y∈X,若x≤y,则a*x=a*y.

证明由引理2知,可设x∈V(b),其中b是X的一个极小元.因b≤x,x≤y,由引理4，得b≤y.再由偏序性，得a*x≤a*b,a*y≤a*b.根据引理7，知a*b∈L(X),即a*b也是X的一个极小元，所以，有a*x=a*b=a*y.

定理7设〈X;*,0〉是一个BCH-代数,Y是X的一个子代数,则

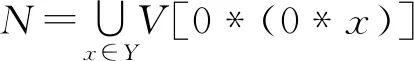
证明根据引理10知, 0*x与0*(0*x)都是该BCH-代数的原子,故V(0*x)与V[0*(0*x)]有意义.

(1) ∀x,y∈M,则∃a,b∈Y,使x∈V(0*a),y∈V(0*b).因为Y是X中的一个子代数,故a*b∈Y.由引理5和引理3的(3)，得

x*y∈V[(0*a)*(0*b)]=V[0*(a*b)]⊆M，

根据引理9,即证明了M是X的一个子代数.

(2) ∀x,y∈N,则∃a,b∈Y,使x∈V[0*(0*a)],y∈V[0*(0*b)].因为Y是X中的一个子代数,故a*b∈Y.由引理5和引理3的(3)，得

x*y∈V{[0*(0*a)]*[0*(0*b)]}=V{0*[0*(a*b)]}⊆N，

根据引理9,即证明了N是X的一个子代数.

定理8设〈X;*,0〉是一个BCH-代数,a是X的一个非0原子,若(0*a)*a=0,则V(0)∪V(a)是X的一个理想.

证明记A=V(0)∪V(a),因0∈V(0),故0∈A.按理想的定义只需证明：若x*y∈A,y∈A,则x∈A，即证明x∈V(0)或x∈V(a).分以下几个情形来讨论.

(1) 设x*y∈V(0),y∈V(0).因V(0)=B(X),由引理11知,V(0)是X的一个理想,故x∈V(0).

(2) 设x*y∈V(a),y∈V(a).由定理1，得

0*[0*(x*y)]=a,0*(0*y)=a，

又由引理3的(3)，得

0*[0*(x*y)]=[0*(0*x)]*[0*(0*y)]=[0*(0*x)]*a,

从而[0*(0*x)]*a=a,再由H-3，得(0*a)*(0*x)=a，两端左乘0并利用引理3的(3)，得[0*(0*a)]* [0*(0*x)]=0*a,因0*(0*a)=a,故a*[0*(0*x)]=0*a.两端右乘a并利用H-3,H-1和引理3的(4)，得0*x=(0*a)*a.最后由已知条件(0*a)*a=0，得0*x=0,所以x∈V(0).

(3) 设x*y∈V(0),y∈V(a).由定理1，得

0*[0*(x*y)]=0,0*(0*y)=a，

又由引理3的(3)，得

0*[0*(x*y)]=[0*(0*x)]*[0*(0*y)]=[0*(0*x)]*a,

从而[0*(0*x)]*a=0.两端左乘0并利用引理3的(3)与(4)和H-1，得(0*x)*(0*a)=0,两端右乘0*x并利用H-3和H-1，得0*(0*a)=0*(0*x),因0*(0*a)=a,故0*(0*x)=a.两端右乘x并利用引理3的(1)，得a*x=0,所以x∈V(a).

(4) 设x*y∈V(a),y∈V(0).由定理1，得

0*[0*(x*y)]=a,0*(0*y)=0，

又由引理3的(3)与(2)，得

0*[0*(x*y)]=[0*(0*x)]*[0*(0*y)]=[0*(0*x)]*0=0*(0*x),

从而0*(0*x)=a.两端右乘x并利用引理3的(1)，得a*x=0,所以x∈V(a).

由定理8和定义6立即得到下面的定理9.

定理9设〈X;*,0〉是一个拟结合BCH-代数,a是X的一个非0原子,则V(0)∪V(a)是X的一个理想.

以上结果是受文献[9-10]的启发而得到的.最后给出一个BCH-代数的BCI-化定理.由引理12知,在BCI-代数〈X;*,0〉中有这样的性质A:若x≤y,则∀z∈X,有z*y≤z*x.作者把这一性质A作为一个条件添加到BCH-代数中来,提出了偏序BCH-代数的概念,且已经找到了是偏序BCH-代数但不是BCI-代数的如下实例.

例设X={0,1,2,3},Y={0,1,2,3,4},X中的二元运算*与Y中的二元运算λ分别由下面的乘法表1，2给出.

乘法表1 X中的二元运算

乘法表2 Y中的二元运算

可以验证〈X;*,0〉与〈Y﹔λ,0〉都是偏序BCH-代数,但不是BCI-代数.因为一般的BCH-代数不具有性质A[12](这里不再举例),故可以说偏序BCH-代数类是BCH-代数类的真子类.

又由引理12知,在BCI-代数〈X;*,0〉中还有性质B：若x≤y,则∀z∈X,有x*z≤y*z.那么能否将性质B作为一个条件添加到BCH-代数中来给出新的一类BCH-代数呢?答案是否定的,即下面的BCH-代数的BCI-化定理.

定理10设〈X;*,0〉是一个BCH-代数,x,y∈X,若x≤y,∀z∈X,有x*z≤y*z,则〈X﹔*,0〉是一个BCI-代数.

证明∀x,y,z∈X,由引理3的(1)，知

[x*(x*y)]*y=0,

即x*(x*y)≤y.

又利用已知条件，得

[x*(x*y)]*z≤y*z,

再由H-3，得

(x*z)*(x*y)≤y*z,

即

[(x*z)*(x*y)]*(y*z)=0，

最后根据引理13知,〈X;*,0〉是一个BCI-代数.

该定理说明在BCH-代数中的3条公理之下由性质B可推出性质A,再根据上面的例子可知,由性质A则不能推出性质B,这就说明性质A比性质B弱一些.