基于美标的全直桩码头振型分解反应谱抗震分析
李成强,孔友南,张 志
(中交第三航务工程勘察设计院有限公司,上海 200032)
高桩码头因其结构简单,能较好适应各类软土地基,且为透空式结构,可避免大面积回填、砂石用料较少等原因在国内外港口建设中得到广泛的应用。高桩码头桩基结构包括斜桩和直桩两种结构形式,斜桩结构能提供较大水平刚度,用以抵抗船舶荷载以及地震荷载[1]。但近年来,尤其在欧美等国,全直桩码头得到更为充分的应用,主要原因如下:结构受力路径简洁明确,方便桩基设计,且利于提高沉桩质量;全直桩结构柔度较大,增大了结构自振周期,地震反应减小;全直钢管桩结构延性较好,在强震作用下可通过较大变形吸收地震能量。随着国内外工程中全直桩码头的广泛应用以及国家“一带一路”倡议的推进,越来越多强震区全直桩码头将会建设,迫切需要对全直桩码头结构的抗震性能开展深入研究。
国内外对于结构抗震的计算方法主要有:振型分解反应谱法、静力弹塑性分析法(pushover法)、动力时程分析法。Pushover法利用侧向力加载将结构推至目标位移,进而确定地震响应,分析方法较为简单,但无法反应高桩码头的扭转变形;动力时程分析法被公认是能反应结构地震响应最接近的方法,但需要选择多条地震波进行计算,占用较多计算机资源,计算用时较长,目前在常规码头设计中较少应用;而振型分解反应谱法计算简单省时,又能在一定程度反映结构的动力特性。由于欧美国家对于抗震研究开展较早,其相关规范在国外工程设计中有较高的认可度,本文以加勒比海地区某全直桩LNG码头为案例,基于美标推算反应谱,采用振型分解反应谱法对全直桩码头结构地震响应进行分析,研究全直桩码头结构的自振特性及结构受力特点。
1 计算方法
ASCE 7-10[2]是美国荷载规范,其抗震设计思路为:确认基本抗震设计参数,即短周期和1 s周期考虑最大危险地震(MCER)的反应谱加速度参数Ss及S1;确定场地放大系数Fa及Fv;计算设计地震反应谱加速度参数SDS=2/3FaSS,SD1=2/3FvS1;按式(1)~(4)推算设计地震反应谱。NFPA 59A-2016[3]是美国液化天然气的生产、存储及处理规范,规定对于LNG码头,需要进行OBE(Operating Basis Earthquake)和SSE(Safe Shutdown Earthquake)两个水准的抗震计算,其中OBE相当于基于ASCE 7-10推出的设计地震(Design Earthquake),设防水准为50 a超越概率10%,而SSE=OBE×1.5,设防水准为50 a超越概率2%。
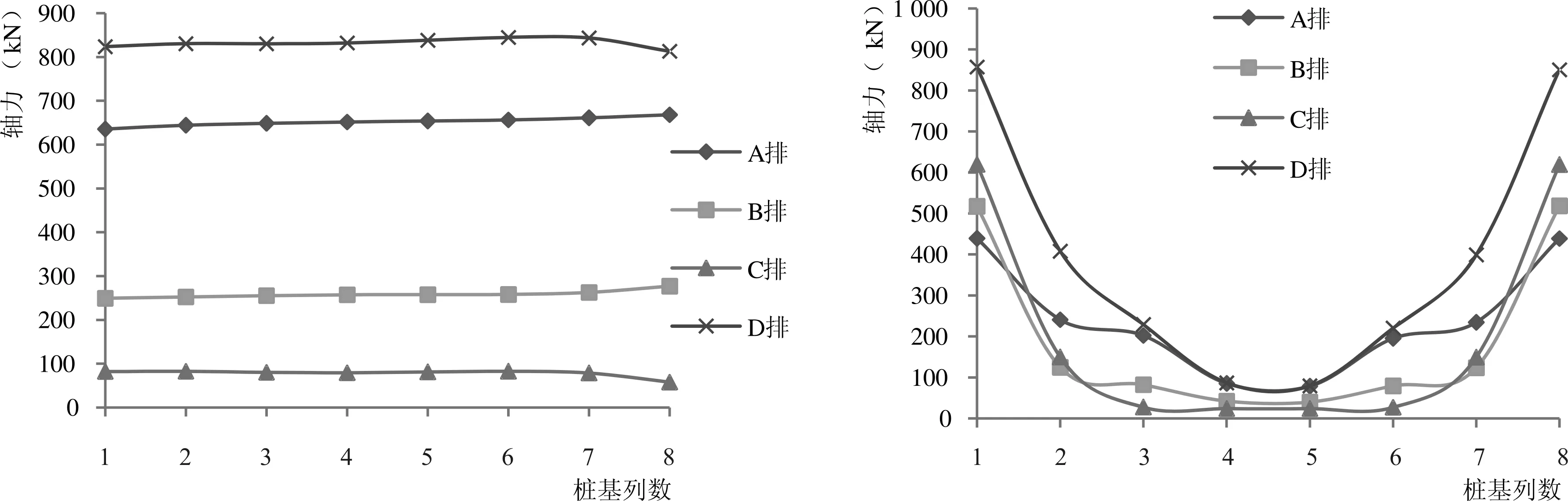
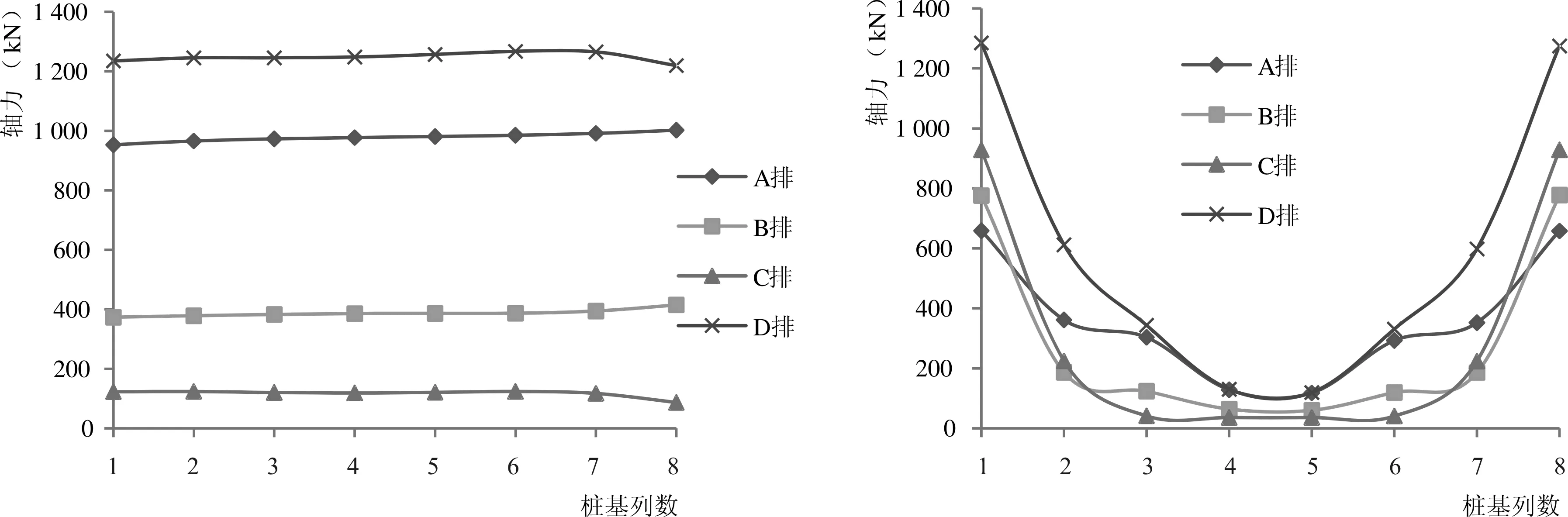
Sa=SDS(0.4+0.6T/T0) (T (1) Sa=SDS(T0≤T≤Ts) (2) Sa=SD1/T(Ts (3) Sa=(SD1TL)/T2(TL (4) 式中:SDS为短周期设计地震反应谱加速度;SD1为1 s周期设计地震反应谱加速度;T为结构基本周期;T0=0.2SD1/SDS;TS=SD1/SDS;TL为长周期过渡周期。 振型分解反应谱法[4]是利用单自由度体系的加速度设计反应谱和振型分解及其正交性原理,进而用来计算多自由度体系地震作用效应的一种方法。本文采用考虑扭转耦联[5]的振型分解反应谱法,求解各阶振型的等效地震作用,再对各振型的地震作用效应进行组合,从而得到多自由度体系的地震作用效应。结构j振型i质点的水平地震作用可按下列公式确定 Fji=αjγjXjiGi (5) (6) 式中:Fji为j振型i质点的水平地震惯性力;Mji为j振型i质点的弯矩;αj为相应于j振型自振周期的地震影响系数,按ASCE 7-10推得的反应谱曲线查找得到;γj为j振型的参与系数;Xji为j振型i质点的水平相对位移;ri为i质点绕转动轴的惯性半径;φji为j振型下i质点的相对扭转角;Gi为i质点的重量。 结构各阶振型下各质点的地震作用可由式(5)和式(6)求得,将求得的地震荷载作用到结构上,得到结构内力及位移的响应。由于各阶振型下结构内力及位移的最大值并不会同时出现,且往往存在几阶振型自振周期相近的情况,需要采用完全二次项组合法(CQC)对各阶振型的最大内力及位移反应进行组合。在运用振型分解反应谱法分析时,需保证振型数量足够,从而使各主要运动方向上的累计参与质量大于90%。本文采用的扭转耦联效应及耦联系数按下列公式[6]计算 (7) (8) 式中:SEk为地震作用的扭转耦联效应;Sj、Sk分别为j、k振型地震作用效应;ρjk为j振型与k振型的耦联系数;ζj、ζk分别为j、k振型的阻尼比;λT为k振型与j振型的自振周期比。 本文以加勒比海地区某全直桩LNG码头的工作平台为计算案例,该工作平台为高桩墩台结构,其平台尺寸为44×22 m,厚度2 m。码头前沿设计底高程为-13.5 m,疏浚坡度1:4,码头面高程为5.5 m。整个工作平台以32根Φ1 500 mm钢管桩支撑,壁厚25 mm,钢管桩伸进墩台1 m。工作平台上主要设备荷载包括操作平台重480 t,4个卸油臂各重55 t,登船梯重40 t,两侧钢便桥各重7.8 t。该工作平台如图1所示,其桩基及主要设备布置如图2所示,桩基由海侧向陆侧分别为A~D排,另一水平方向桩基布置分别为1~8列。 图1 工作平台断面图(高程单位:m,其余单位:mm)Fig.1 Section of working platform图2 桩基及主要设备平面布置图(单位:mm)Fig.2 Pile and equipment plan of working platform 鉴于该全直桩码头工作平台在水平方向尺寸较大,可认为在平面内平台的抗弯及抗剪刚度均远大于桩基刚度。在水平荷载作用下,上部墩台在水平面内变形很小,忽略不计,可将该全直桩码头视为由混凝土墩台通过若干桩顶连接下方桩基而构成的空间墩台桩系结构。本文采用通用有限元分析软件Robot建立三维有限元模型进行数值分析,对于空间的墩台桩系结构,采用杆单元模拟桩基,上部墩台采用壳单元模拟。桩基和墩台之间采用刚性连接,桩底按弹性嵌固法考虑,嵌固深度按下式[7]计算 表1 地基主要参数表Tab.1 Foundation parameters 表2 材料参数一览表Tab.2 Material parameters t=ηT (9) (10) 式中:t为嵌固点距泥面深度;T为桩的相对刚度系数;η为系数,取1.8~2.2;EP为桩材料弹模;IP为桩截面惯性矩;m为桩侧地基土的水平抗力系数随深度增长的比例系数;b0为桩的换算宽度。另外桩基壁厚考虑3 mm防腐预留,模型中仅取22 mm。地基主要参数见表1,经计算,嵌固点深度取为5倍桩径。 本次模型整体坐标系的原点取为邻近A1桩的墩台角点,由海侧指向陆侧为X正方向,由A1桩指向A8桩方向为Y正方向,Z方向垂直于墩台平面,竖直向上为Z正方向。有限元模型如图3所示。 图3 有限元模型示意图Fig.3 Finite element model 上部墩台为现浇混凝土结构,下部桩基为钢管桩,模型主要材料参数见表2。 本工程风险等级(Risk Category)为Ⅲ级,场地分类为D类,短周期和1 s周期考虑最大危险地震(MCER)的反应谱加速度参数分别为Ss=0.96 g,S1=0.40 g。根据ASCE 7-10规范:短周期和1 s周期的场地放大系数分别取为Fa=1.1,Fv=1.6,由此根据式(1)~(4)可以推出美标的设计地震(Design Earthquake)反应谱。根据NFPA 59A-2016规范,对于LNG码头,进行OBE和SSE两个水准的抗震计算,其中OBE相当于基于ASCE 7-10推出的设计地震(Design Earthquake),而SSE=OBE×1.5。 本文采用子空间迭代法对全直桩码头结构自振特性进行分析,表3列出了前6阶模态分析结果,包括自振周期、频率、各阶模态不同方向的振型质量参与系数。根据表3可以发现,3个主要振动方向(UX、UY、RZ)的前三阶振型,其振型质量参与系数的值累加均超过ASCE 7-10要求的90%,且因在进行抗震分析时,以水平地震为主,所以前三阶振型可以作为该结构的主振型。可以看出,1阶振型以Y方向平动为主,同时伴随绕Z轴的水平扭转;2阶振型为X方向平动振型;3阶振型以绕Z轴的水平扭转为主,伴随Y方向的平动。因此,1阶和3阶振型皆为平动和水平扭转耦合振型,2阶振型为平动振型,以上平扭耦合、平动振型的分析结论也与下文位移及弯矩分析相对应。另外,前三阶振型的周期比较接近,这也证明使用CQC组合法而非SRSS(平方和开平方根)法进行振型组合的必要性。 表3 前6阶自振周期及各方向振型参与系数Tab.3 Natural vibration period and model mass participation ratio 本文采用振型分解反应谱法,按照美标中OBE和SSE两个水准的地震分别从X、Y两个方向对码头结构进行地震动激励,并按照CQC法对各阶振型的最大内力及水平位移反应进行组合。图4给出了两个水准不同方向地震作用下的前三阶桩顶位移反应,可以看出,与自振分析相一致的是:2阶振型为X方向平动振型,此时所有桩的桩顶位移几乎一样;1阶、3阶为平扭耦合振型,各根桩的桩顶位移差异较大,其中1阶振型A排桩的位移较大,4、5列桩位移较小,在Y向地震激励下尤为明显,主要因为码头海侧桩自由长度较长,且设备荷载布置偏向码头海侧,模型整体质量中心和水平刚度中心位置偏离,Y向地震几乎垂直于质量中心和刚度中心的连线方向;而3阶振型1、2、7、8这4列边桩位移较大,3、4、5、6这4列中间桩位移较小,原因为3阶振型以绕Z轴的扭转为主。以上分析说明:在码头上布置设备时宜尽量靠近码头面中心或双轴对称布置,以减少扭转破坏,或适当调整桩基布置,增强抗扭刚度。 1阶2阶3阶4-a OBE水准X方向地震 1阶2阶3阶4-b OBE水准-Y方向地震 1阶2阶3阶4-c SSE水准-X方向地震 1阶2阶3阶4-d SSE水准-Y方向地震图4 桩顶位移Fig.4 Displacement of pile top 另由图4可知,相同方向地震作用下,OBE水准地震各阶振型的桩顶位移是SSE地震下的三分之二,这与美标NFPA 59A-2016规范中对两个水准地震的定义相符,OBE设防水准为50 a超越概率10%(回归期475 a),SSE设防水准为50 a超越概率2%(回归期2 475 a),一般来讲,对于全直桩码头,位移大小以OBE水准控制,强度则以SSE水准来控制。 5-a OBE-X5-b OBE-Y 5-c SSE-X5-d SSE-Y图5 桩基轴力Fig.5 Axial force of pile 图5给出了OBE和SSE水准下两个水平方向地震作用时的桩基轴力分布图,该轴力为CQC组合下的轴力绝对值,仅考虑地震作用引起的轴力进行分析。可以看出:在X向地震作用下,A、D两排边桩的轴力明显大于B、C两排中桩,且陆侧D排桩轴力最大;在Y向地震作用下,1、8两列边桩的轴力明显大于2~7列桩,4、5两列中桩轴力最小,同样陆侧D排桩轴力大于其他三排,最大轴力产生于D1角桩。以上桩基轴力分布特征与美国全直桩码头陆侧桩内力较大,承担较多水平力而作为抗震桩[8]的概念相符。可知:在工程设计时应注意边桩和角桩的内力,适当加强边角桩与上部结构的连接;同时适当加强或加密陆侧桩群,合理地提高水平承载能力。 图6给出了SSE水准两个方向地震作用下的前三阶桩顶弯矩分布图,分为Mx和My。可以看出,在两个方向水平地震作用下,2阶振型的桩顶弯矩Mx及My分布规律均为D排>C排>B排>A排,每排中各桩的桩顶弯矩相差不大,且X向地震作用下My远大于Y向地震作用,这是由于2阶振型为X向平动振型,同时由海侧向陆侧桩的自由长度逐渐变短,2阶振型桩顶位移基本相同,则陆侧桩承担更多的弯矩,这与上文自振分析、桩顶位移分析相符。对比两个方向地震作用下的1阶振型,可知Y向地震作用下的Mx及My均远大于X向地震作用,且My的分布规律均为两侧边桩较大,中间桩较小,这是由于1阶振型以Y方向平动为主,同时伴随绕Z轴的水平扭转。分析3阶振型,可以发现类似1阶振型的桩顶弯矩分布规律,My最大值均为D1和D8角桩,这是由于3阶振型以绕Z轴的水平扭转为主,伴随Y方向的平动。因此在桩基设计时,可适当加强边角桩与上部墩台的连接,加强桩基的抗扭能力,同时优化上部设备的布置,尽量减少扭转效应。 1阶2阶3阶6-a SSE-X向地震-Mx 1阶2阶3阶6-b SSE-Y向地震-Mx 1阶2阶3阶6-c SSE-X向地震-My 1阶2阶3阶 6-d SSE-Y向地震-My 考虑结构自重、设备荷载、地震荷载等作用,对上部墩台的弯矩进行计算分析。图7给出了OBE和SSE水准地震作用下墩台弯矩分布图,根据ASCE 7-10,该弯矩按±1.0Mx±0.3My及±0.3Mx±1.0My对不同方向地震作用效应进行组合。由图7可以发现:在水平地震荷载作用下,桩基位置对应的墩台区域上拱较为明显,该区域内X方向及Y方向弯矩均明显增加,进一步形成上部受拉的弯矩密集区(已在图7中标记),在设计墩台顶部配筋时,墩台顶部密集区内宜适当加密,一般区域内配筋可适当减少,降低造价,增强结构的经济性。 7-a OBE-Mx7-b OBE-My 7-c SSE-Mx7-d SSE-My图7 墩台弯矩Fig.7 Bending moment of the deck 本文基于美标,采用振型分解反应谱法对全直桩码头进行抗震计算分析,为日后类似工程设计提供参考,主要结论如下: (1)对于上部设备偏心布置,整体质量中心偏离水平刚度中心的全直桩码头,其前3阶振型起主要作用,1、3阶振型为平扭耦合振型,1阶振型平动为主,伴随着扭转;3阶振型扭转为主,伴随着平动;2阶振型为平动振型。设计时可尽量将设备靠近码头面中心或双轴对称布置,减少扭转破坏,或适当调整桩基布置,增强抗扭刚度。 (2)在X、Y向地震作用下,边桩、角桩的轴力、弯矩明显大于中间桩,设计时应适当加强边角桩与上部结构的连接。陆侧桩的轴力最大,这与美国全直桩码头陆侧桩内力较大,承担较多水平力而作为抗震桩的概念相符,设计时宜适当加强或加密陆侧桩群,合理增强水平承载力。 (3)地震作用下,桩基位置对应的墩台区域上拱明显,局部形成上部受拉密集区,墩台顶部配筋时,密集区内宜适当加密,一般区域内配筋可适当减少。2 计算模型
2.1 工程背景
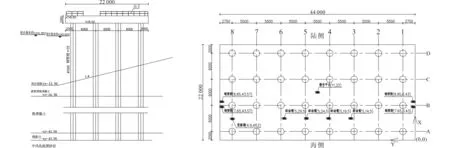

2.2 模型建立
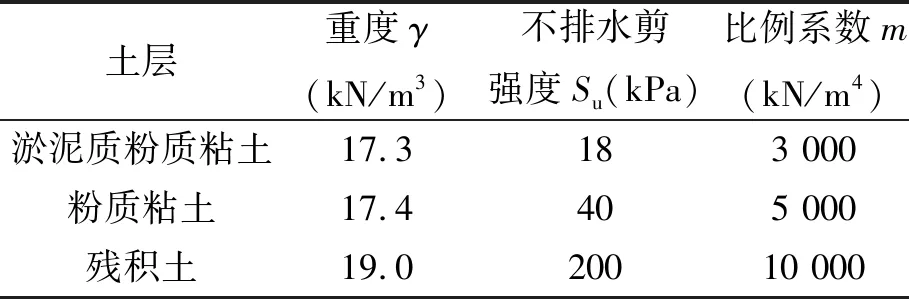

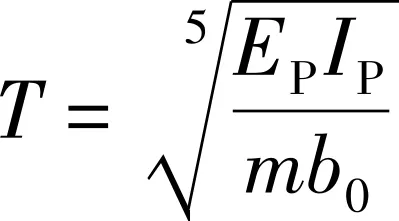

2.3 反应谱推算
3 抗震计算分析
3.1 结构自振分析
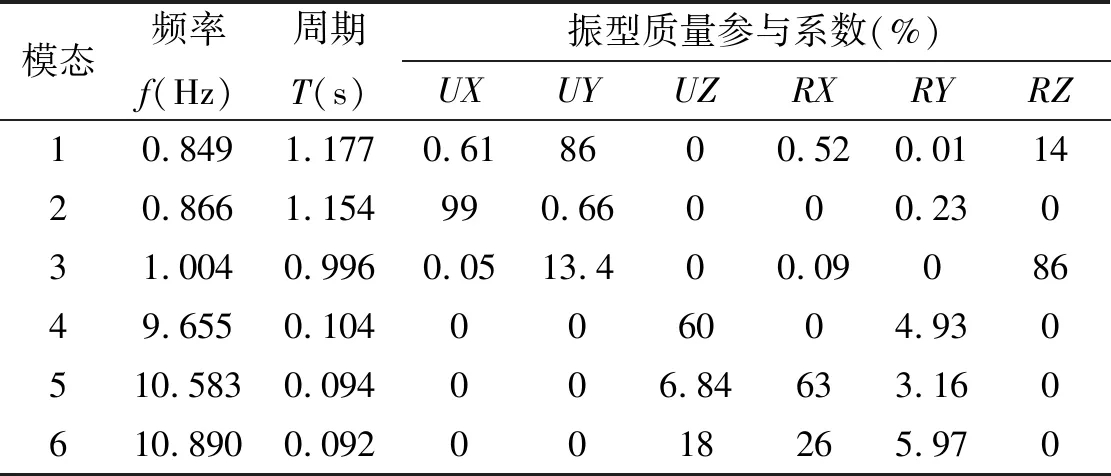
3.2 桩顶位移









3.3 桩轴力
3.4 桩顶弯矩







图6 桩顶弯矩
Fig.6 Bending moment of pile top3.5 墩台弯矩




4 结论

