基于Fluent斜坡海堤挡浪墙受力特性数值计算研究

杨成刚，丁 洁 ，郝嘉凌 ，邹 恒

(1.河海大学 港口海岸与近海工程学院，南京 210098；2.中交上海航道勘察设计研究院有限公司, 上海 200136；3.上海市政设计研究院，上海 200092)

江苏省海岸线长达954 km，沿中部地区独特的动力地貌蕴育了长约200 km、宽约90 km的辐射沙脊群，对其匡围类型有边滩垦区和岸外沙脊垦区。岸外沙脊垦区匡围的技术较边滩匡围难度大。由于新匡围区将建设成为重要港口工业集聚区、宜居沿海城镇区、富有特色的滩涂海滨旅游区，不仅有力地推动沿海经济的发展，还能增加就业与社会有效供给，以及改善生态环境，保障经济社会的可持续发展。对此，新匡围区海堤工程结构的坚固与稳定尤为重要，需能确保新匡围区内免受风暴潮、风浪侵袭，其损毁将会造成巨大的经济损失[1]。

海堤堤顶设挡浪墙一方面抵御波浪，另一方面节约断面土石方量[2]。对于挡浪墙结构承受的波浪力值，大多采用物理模型试验研究确定，近年来也有采用波浪数模进行研究。例如：Martin[3]从波浪爬高角度计算防浪墙的波浪力和作用高度，并相应采用物理模型验证。琚烈红[4]通过物理模型分析直立式和圆弧式防浪墙所受波浪力差异。王登婷[5]通过物理模型讨论防浪墙底面高程对其迎浪面及底面上的波浪压强及整体稳定性的影响；王颖[6]在防浪墙上安置三分力天平，直接测其所受的波浪力，并分析不同防浪墙和堤坝组合对其所受波浪力和越浪量的影响，以及防浪墙的整体稳定性。Kortenhaus[7]等较系统地研究了直立堤曲线形式防浪墙对其越浪量和波浪力的影响。刘子琪等[8]对防波堤工程弧形防浪墙防浪效果进行试验研究，对比不同结构型式防浪墙的防浪效果，证明弧形结构防浪最为有效。焦颖颖[9]和Liu[10]等基于Fluent 软件平台建立了二维数值波浪水槽，对规则波作用下不同弧形防浪墙的水动力特性进行了分析研究。

本文基于Fluent软件，对江苏海堤工程堤顶直立型和半圆弧型挡浪墙迎浪面受力进行数值计算，分析研究其受力规律及特性。

1 工程概况

江苏省南通市通州湾腰沙围垦二期通道工程地处岸外辐射沙脊群区，其东西向通道长3.025 km，南北向通道长2.950 km，东西向通道与南北向通道呈“L”型垂直相接，总长度5.975 km(图1)。东西向通道斜坡堤设计断面(以下简称：设计断面)尺度为：断面底高程为1.7 m，挡浪墙顶高程11.4 m(85国家高程、下同)、顶宽30 cm、底高程9.6 m、底宽1.80 m；斜坡堤为单坡，内外坡坡比m=2.0，外坡护面结构采用1.5 t扭王块体、镇压层长19 m、面层块石重150～300 kg；护底结构块石50～100 kg(图2)。

由于工程区域自然条件极为恶劣，当地建设的海岸堤防工程结构屡遭破坏。为此，基于数值波浪水槽理论，对腰沙围垦二期通道工程海堤设计断面挡浪墙受力特性进行数值模拟，分析研究所受波浪力大小及其变化特点。

注：①抛石50～100 kg 厚0.8 m；②抛石护底150～300 kg；③1.5 t扭王字块，厚1.18 m；④袋装砂被；⑤吹填砂；⑥1 t扭王字块厚1.03 m。图2 通州湾腰沙围垦二期通道工程设计断面结构示意图Fig.2 Sketch of design section of the second phase passageway project of Tongzhou bay Yaosha reclamation

2 数学模型

2.1 控制方程

对于二维不可压缩的自由流动流体，粘性系数为常数，控制性方程由连续性方程和动量方程组成。

连续性方程

(1)

动量方程

(2)

(3)

式中：u和v分别为x和y两个方向的速度分量；ρ为流体密度；μ为动力粘性系数；g为重力加速度；Fx和Fy分别为x和y两个方向的附加动量源项。

2.2 造波、消波方法

基于N-S方程和VOF方法的波浪数值水槽，在造波区和消波区引入解析松弛方法，其原理是对各区域每时刻的速度和压力按照以下关系进行实时更新。

um=Cul+(1-C)uj

(4)

pm=Cpl+(1-C)pj

(5)

式中：ul表示期望得到的速度，uj表示在区域内速度的修正量，um表示最终得到的速度结果，pl表示期望得到的压力，pj表示在区域内压力的修正量，pm表示最终得到的压力结果，下同。C=C(x)为与空间位置有关的光滑过渡的加权函数。造波区和消波区具有不同的表达式。

对附加动量源项，可以采用忽略粘性的欧拉方程来确定。通过数值方法对包括添加和未添加源项的欧拉方程进行离散化处理，得到各区的源项表达式如下。

造波区

(6)

(7)

左消波区

(8)

(9)

右消波区

(10)

(11)

将各区附加动量源项表达式通过软件自带的接口代入到动量方程式(2)中，从而实现造波和消波。

2.3 压力速度耦合方式

在使用分离求解器时，通常可以选择SIMPLE、SIMPLEC、PISO算法，本文模拟时选择了PISO算法，因为它是专门针对瞬态问题而设计的算法。PISO算法与SIMPLE和SIMPLEC不同之处在于增加了一个修正步，即由预测压力等变量—修正—再修正三个步骤组成，而SIMPLE和SIMPLEC算法只包括前两个步骤。PISO算法的这种优点不但能使得修正值能更好地满足动量方程和连续性方程，而且可加快单个迭代步中的收敛速度[11]。

2.4 压力插值格式

当使用分离求解器时可以采用很多压力插值格式，对于大多数情况,标准格式已经足够了,但是对于特定的某些模型使用其它格式可能会更好：(1)对于具有较大体积力的问题,推荐使用体积力加权格式。因本文模型有较大的重力故选择体积力加权格式。(2)对于具有高涡流数,高雷诺数自然对流,高速旋转流动,包含多孔介质的流动和高度扭曲区域的流动,使用PRESTO格式。(3)对于可压流动推荐使用二阶格式[11]。

3 数值模型建立及验证

3.1 数值波浪水槽建立

数学模型试验构建的数值波浪水槽见图3，其比尺采用1: 1。依据设计断面堤前设计水位及其通道断面尺寸，数值波浪 水槽总长度取600 m，高度取13.0 m，波浪的造波区长度取60 m，前端消波区长度取80 m，工作区长度取360 m，末端消波区 长度取100 m。数值水槽网格划分如图4所示，横向网格间距取1.0 m，竖向初始间距为0.8 m，竖向网格疏 松比为0.9，全局水槽最小网格面积为0.4 m2，最大面积为1.464 m2。据来波向，左侧设置为对称边界，顶部 为压力入口，其他部分边界均设置为固壁边界。

图3 数值波浪水槽示意图
Fig.3 Schematic diagram of numerical wave flume

2

2

3.2 计算参数设置

沿数值波浪水槽长度方向从造波边界初始位置起，在x=150 m，x=250 m处设置波面监测面来监测工作区波浪自由面数据。

对于每个监测面，其波面水位值hw(x,t)为

(12)

式中：Φ为监测面处网格内水的体积分数；Aj为监测面处网格的面积。

波面水位值减去平均水位值，即可得到该监测面的波高值h(x,t)

(13)

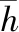
设置好监测器后，对数值波浪水槽所有计算区域进行初始化，压力方程采用体积力加权格式，压力速度耦合方式采用PISO算法。设置迭代步长为0.05 s，迭代步数为1 800次，模拟数值波浪水槽90 s造波过程。

3.3 海堤工程波浪断面数值模型构建及验证计算

图4 东西向通道设计断面网格划分情况Fig.4 Mesh layout of east west passageway design section

在数值波浪水槽平台段放置海堤设计断面(镇压层前端位于水槽x=290 m处)，模拟验证计算设计断面在水位8.13 m(50 a一遇极端高水位)，H1%=3.77 m，T=8.09 s条件下挡浪墙墙面受力状况，其网格划分见图4，直立式挡浪墙及测力点的布置见图5(墙前不安放人工块体)。经模拟计算得到直立式挡浪墙墙面波压力大小，并与已有的物模试验结果[12]进行比较(表1)，两者误差在5.0%以内。

表1 直立式挡浪墙迎浪面波压力物模试验与 数模计算结果验证Tab.1 Physical model test and numerical simulation verification of wave pressure on waveward side of vertical parapet wall kPa

注：高程单位为m，其他均为mm。 5-a 直立式 5-b 半圆弧式图5 挡浪墙测力点布置图Fig.5 Layout of measuring points for parapet wall

4 斜坡式海堤挡浪墙受力波浪数值模拟计算及其特性研究

基于构建的波浪水槽海堤数值模型，计算分析设计断面挡浪墙前不安放人工块体，墙体承受波压力大小及其分布，探究不同波要素组合工况对挡浪墙墙面波压力的影响规律[13]，对此，挡浪墙波压力数值计算中考虑2种挡浪墙型式(直立型挡浪墙、半圆弧型挡浪墙)以及斜坡坡比(i=1:2和1：2.5)，进而比较分析不同挡浪墙型式(图5)与斜坡坡比对波压力分布及波浪力大小的影响特性。

4.1 数值模型试验组合

表2 海堤挡浪墙波浪数值模拟计算工况Tab.2 Numerical simulation of wave conditions for parapet wall of sea dike

注：计算工况组合为27组，括号内数字表示组次顺序。

为探究波要素变化对于不同型式挡浪墙承受波压力的影响规律，选取3个堤前水深、各自与3个波高、3个波周期进行组合，得到27组不同波要素试验工况(表2)。各工况模拟计算结果见表3、表4。

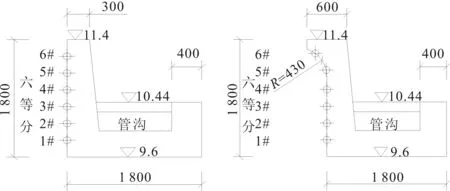
表3 直立型及半圆弧型挡浪墙数值模拟测点压力试验值(坡比1：2.0)Tab.3 Numerical simulation of pressure test points for vertical and semicircular arc parapet wall (slope ratio 1:2.0) kPa

注：括号外代表直立型挡浪墙测点压力；括号内代表半圆弧型挡浪墙测点压力。

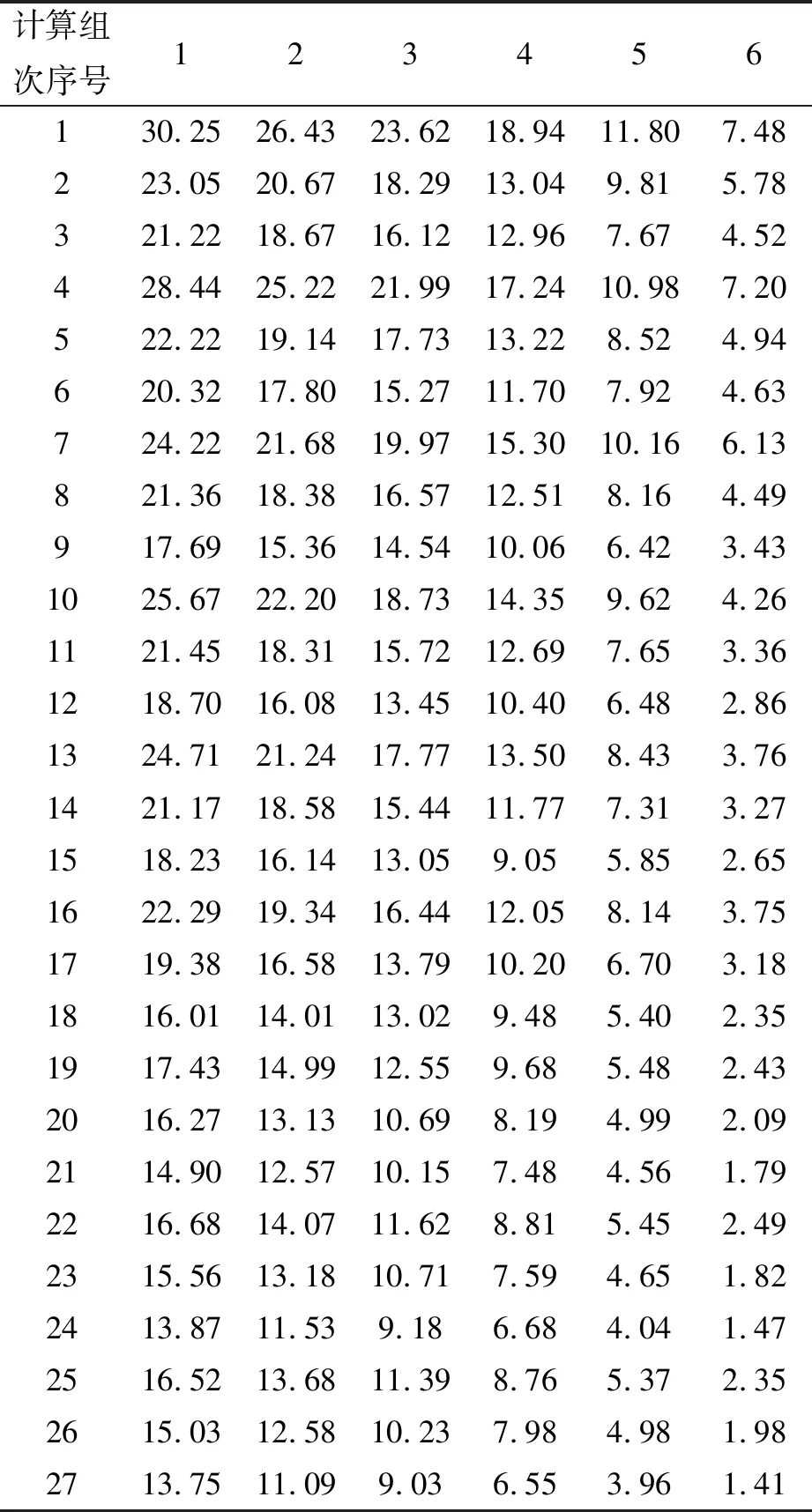
表4 直立型挡浪墙数值模拟测点压力试验值(坡比1:2.5)Tab.4 Numerical simulation of pressure test points for vertical parapet wall(slope ratio 1:2.5) kPa

4.2 不同型式挡浪墙迎浪面波压力计算与分析

(1)斜坡堤堤前水深对不同型式挡浪墙墙面波压力的影响。

取代表工况波高为3.77 m、波周期为8.09 s，计算结果如图所示(图6)。不同堤前水深条件下，作用于直立型和半圆弧型挡浪墙迎浪面波压力沿墙体分布近似三角形形状，测点波压力值衰减较均匀，最大波压力值位于挡浪墙体底板。由于半圆弧型挡浪墙顶端反弧挑浪，降低堤顶越浪量，对此，经斜坡面上爬水体对挡浪墙的波击作用，其迎浪面承受的波压力也大于直立型挡浪墙墙面波压力，增大幅度为2%～30 %。随着水深降低，不同型式的挡浪墙承受的波压力也随之减小，其分布与受力特点基本不变，随水深6.43 m降低到5.94 m，直立型挡浪墙各测点波压力减小幅度为37%～72%，半圆弧型挡浪墙各测点波压力减小幅度为50%～62%。

(2)入射波波高对不同型式挡浪墙墙面波压力的影响。

取代表工况堤前水深d=6.43 m，波周期T=8.09 s，工况计算结果如图所示(图7)。相同水深不同入射波高条件下，直立型和半圆弧型挡浪墙迎浪面各测点的波压力均随入射波波高增大而增大，半圆弧型挡浪墙迎浪面波压力变化趋于平缓。随波高3.15 m增大到3.77 m，直立型挡浪墙各测点波压力增大幅度为4%～61%，半圆弧型挡浪墙各测点波压力增大幅度为8%～47%。

(3)入射波波周期与斜坡坡度变化对挡浪墙墙面波压力的影响。

取代表工况各级水位在波高H=3.77 m的计算结果如图8所示。考虑斜坡堤坡比分别为1:2.0和1:2.5，在不同入射波波周期条件下，直立型挡浪墙墙体迎浪面各测点的波压力随入射波波周期的增大而增大(图8)，随波周期7.03 s增大到8.09 s。

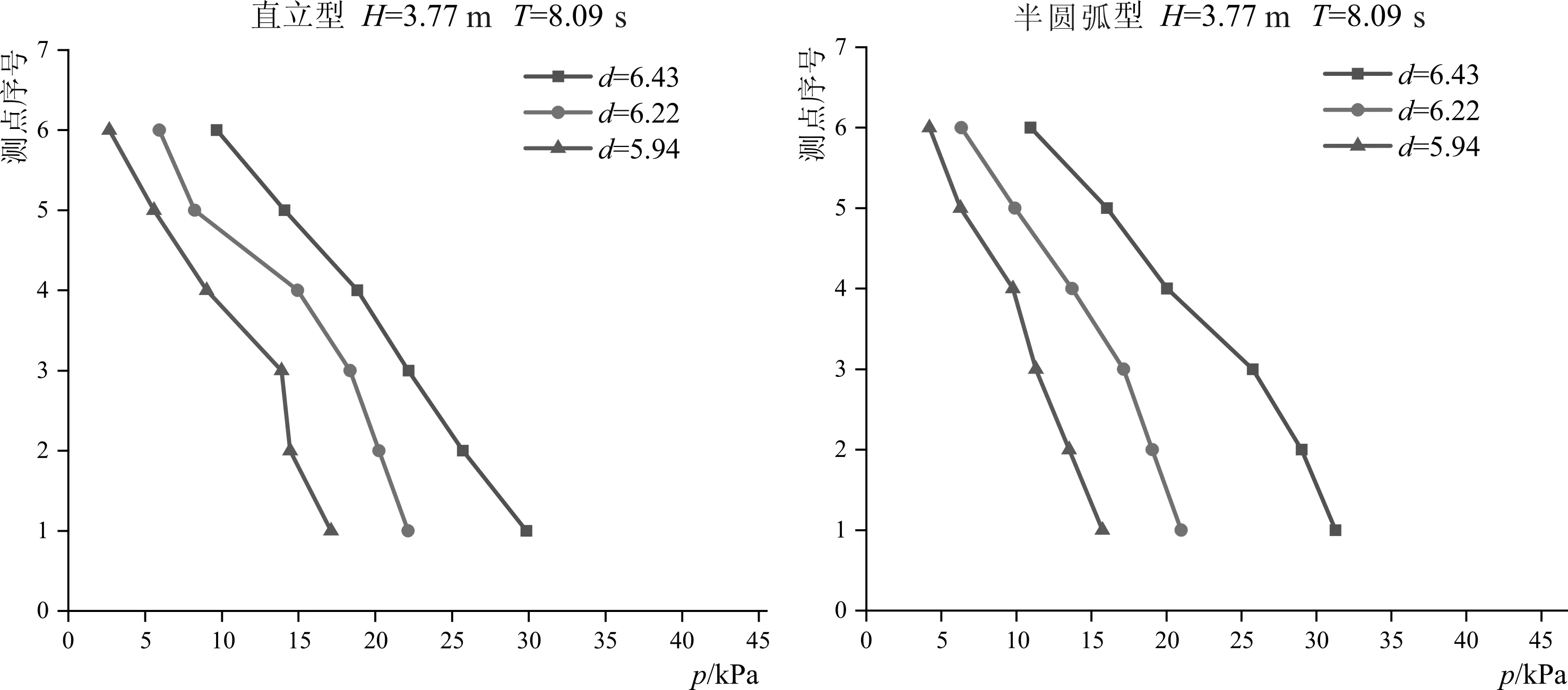
图6 挡浪墙迎浪面波压力与堤前水深的关系Fig.6 Relationship between wave pressure and water depth of breakwater wall

A：水深为6.33 m时坡比1:2直立型挡浪墙各测点波压力增大幅度为16%～80%，坡比1:2.5直立型挡浪墙各测点波压力增大幅度为42%～65%；

B：水深为6.22 m时坡比1:2直立型挡浪墙各测点波压力增大幅度为12%～65%，坡比1:2.5直立型挡浪墙各测点波压力增大幅度为37%～50%；

C：水深为5.94 m时坡比1:2直立型挡浪墙各测点波压力增大幅度为24%～58%，坡比1:2.5直立型挡浪墙各测点波压力增大幅度为17%～36%；

坡比1:2.5直立型挡浪墙迎浪面测点的波压力在较高水位下比坡比1:2.0直立型挡浪墙偏小，减小幅度为7%～40 %，在较低水位下比坡比1:2.0直立型挡浪墙偏大，增大幅度为2%～25 %。

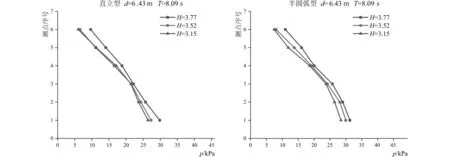
图7 挡浪墙迎浪面波压力与入射波波高的关系Fig.7 Relationship between wave pressure and incident wave height at waveward side of parapet wall

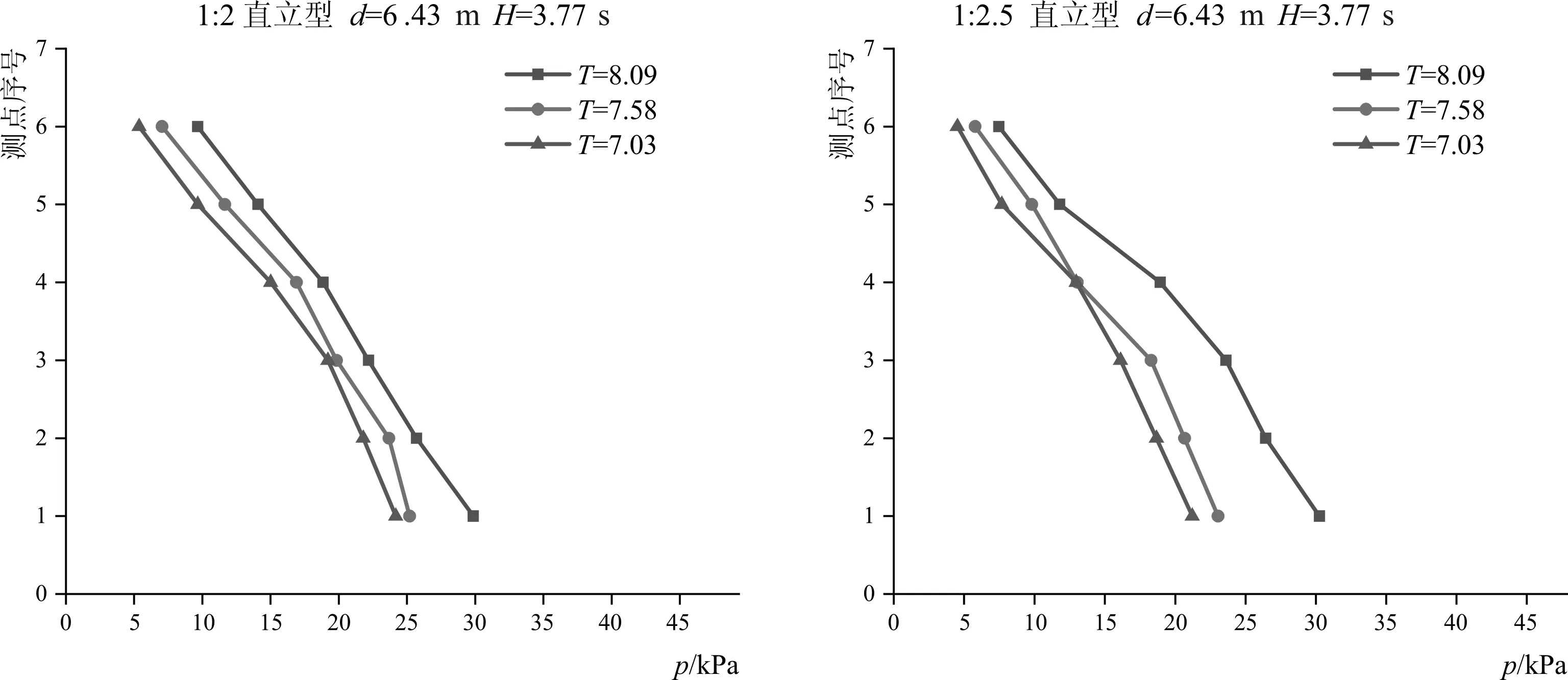
8-a d=6.43 m

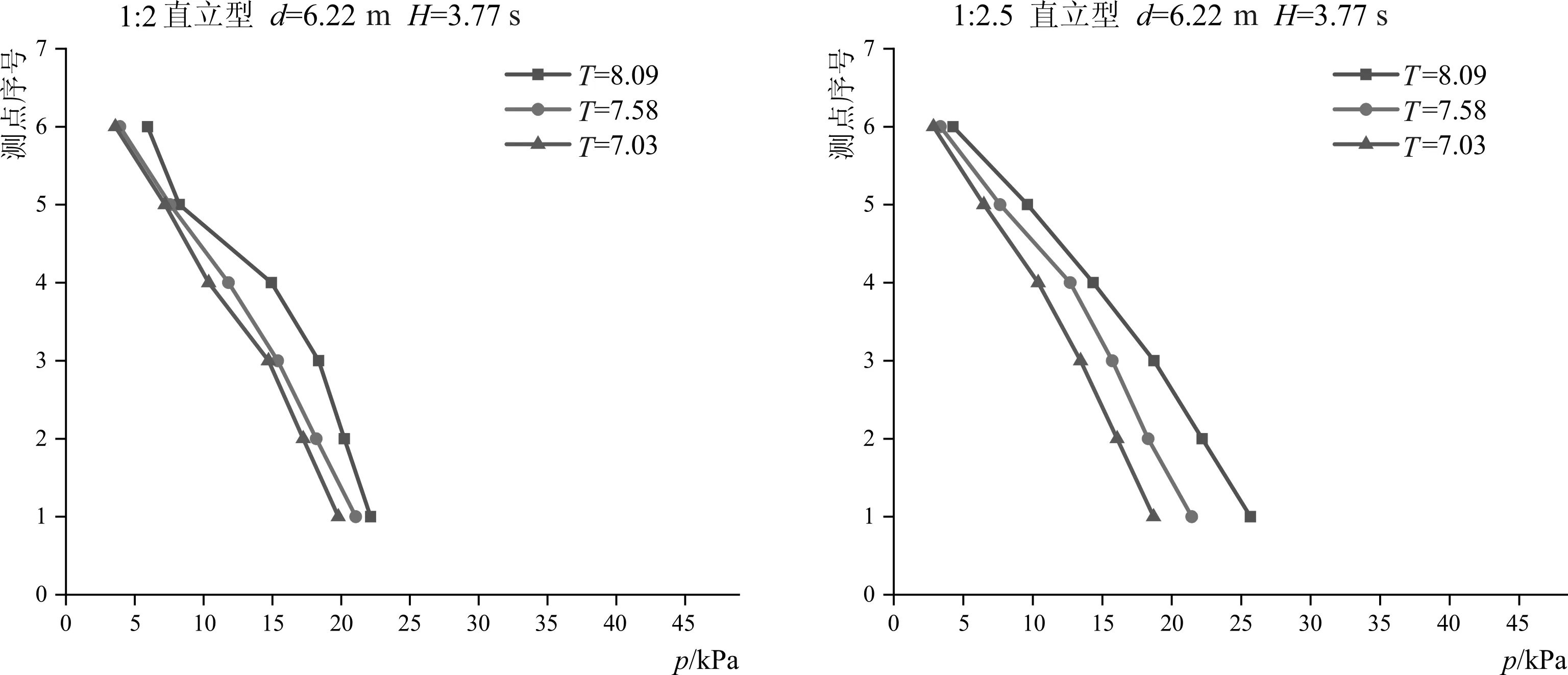
8-b d=6.22 m

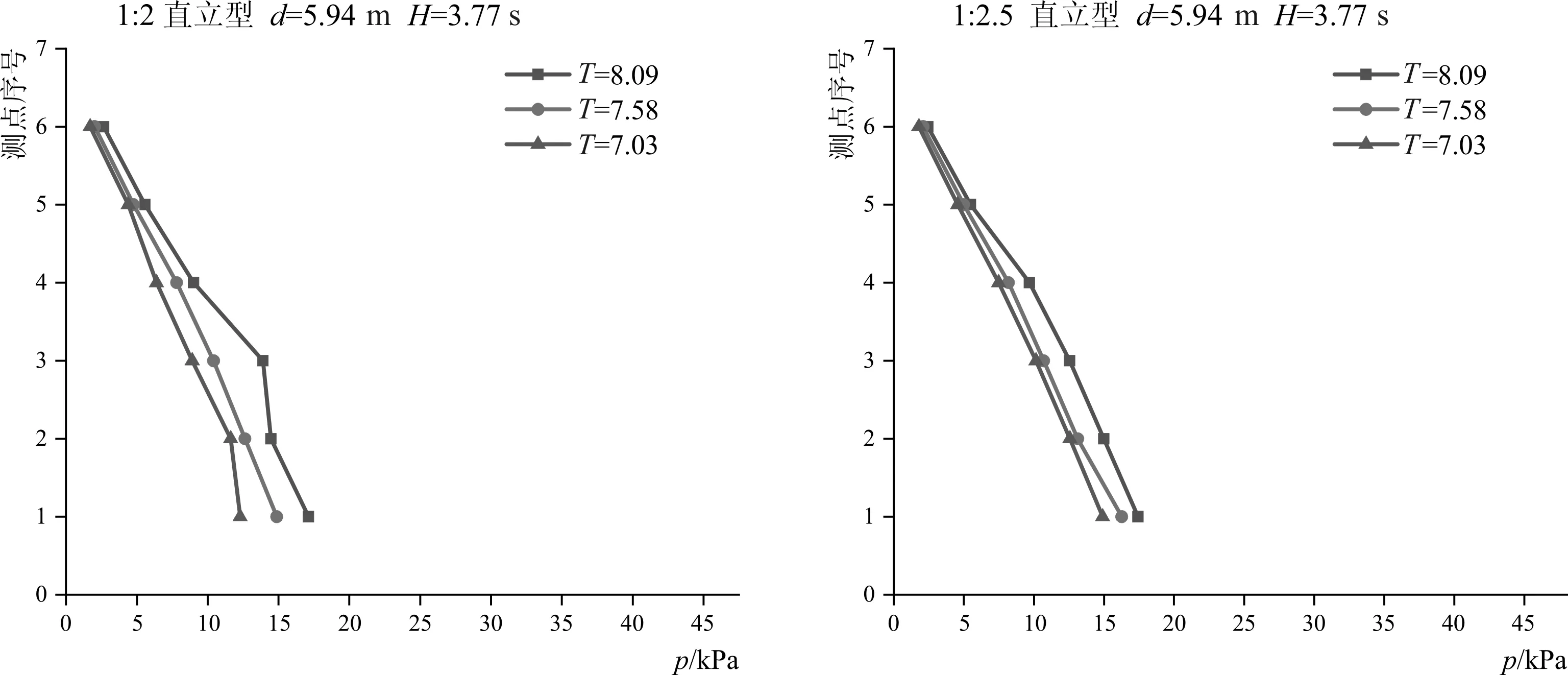
8-c d=5.94 m图8 挡浪墙迎浪面波压力与入射波波周期的关系Fig.8 Relationship between wave pressure and incident wave period at waveward side of parapet wall

4.3 不同型式挡浪墙波浪力特性的对比分析

表5 挡浪墙波浪力特性分析选取工况Tab.5 Selection of working conditions of wave force characteristic analysis of parapet wall

影响斜坡式海堤堤顶挡浪墙承受波浪力的因素比较多，也比较复杂，如来波波高H、波坦L/H、水深(堤前水深d和墙前水深d1，当静水面在挡浪墙墙底面以下时墙前水深d1为负[14]，由于水位7.64 m、7.92 m、8.13 m均在墙底面高程9.6 m以下，墙前水深分别为-1.96 m、-1.68m、-1.47 m)、斜坡坡度以及挡浪墙结构型式，其中以入射波波要素和墙前水深影响为主。为分析挡浪墙承受波浪的特性，选取最大波高工况(表5)进行分析，考虑到该海堤设计断面控制水位范围，则墙前相对水深d1/H取在-0.52～-0.39。

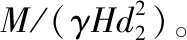
(1)相对水深和波坦变化对不同结构型式挡浪墙墙体承受波浪力的影响。

在墙前相对水深d1/H从-0.52到-0.39的变化范围内(图10～图12)，作用在挡浪墙上的水平波浪力、垂直波浪力和总波浪力矩都随着墙前相对水深的增大而增大(如坡比1：2.0直立型挡浪墙波坦为15.70时，水平波浪力从0.28增加到0.53、垂直波浪力从0.23增加到0.40、总波浪力矩从0.25增加到0.48，增大幅度为74%～92%)；在波坦L/H从13.08到15.70的变化范围内，作用在挡浪墙上的水平波浪力、垂直波浪力和总波浪力矩也是随着波坦的增大而增大(如坡比1：2.0直立型挡浪墙相对水深为-0.39时，水平波浪力从0.42增加到0.53、垂直波浪力从0.32增加到0.40、总波浪力矩从0.37增加到0.48，增大幅度为25%～30%)。由此可知在波浪坦度较大的地方，为提高挡浪墙的稳定性，降低波浪力及倾覆力矩，可增加挡浪墙底板宽度。

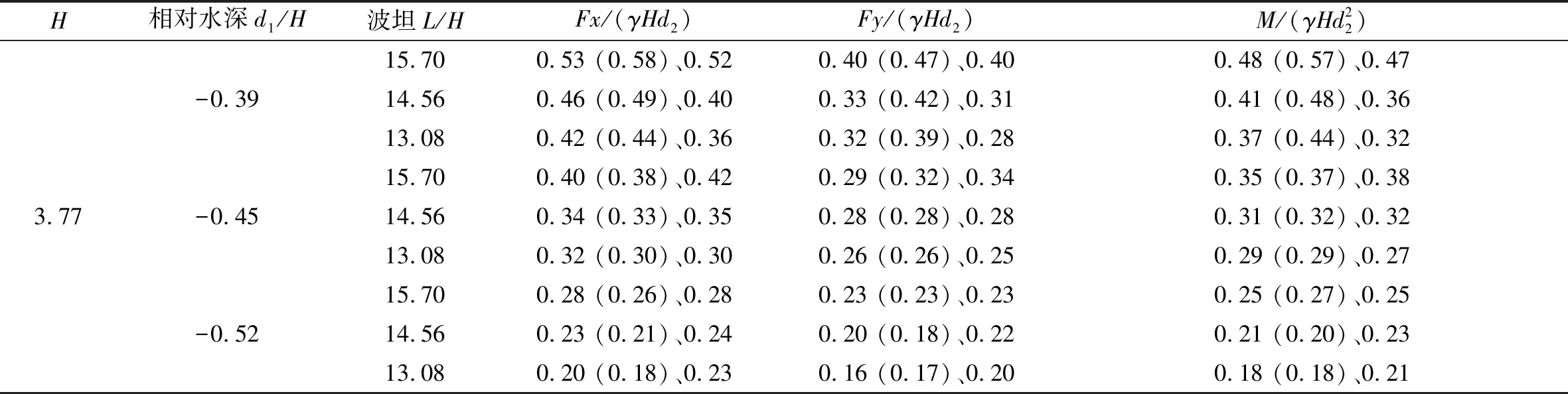
表6 直立型及半圆弧型挡浪墙数值模拟无量纲波浪力值(坡比1：2.0、1:2.5)Tab.6 Numerical simulation of dimensionless wave force for vertical and semicircular arc parapet wall(slope ratio 1:2.0，1:2.5)

注：坡比1:2.0时直立型挡浪墙无量纲波浪力值(括号内为半圆弧型挡浪墙无量纲波浪力值)、坡比1:2.5时直立型挡浪墙无量纲波浪力值。

图10 直立型挡浪墙水平波浪力与相对水深和波坦的关系曲线Fig.10 Relationship between horizontal wave force and relative water depth and wave flat of vertical parapet wall图11 直立型挡浪墙垂直波浪力与相对水深和波坦的关系曲线Fig.11 Relationship between vertical wave force and relative water depth and wave flat of vertical parapet wall图12 直立型挡浪墙波浪总力矩与相对水深和波坦的关系曲线Fig.12 Relationship between wave total moment and relative water depth and wave flat of vertical parapet wall

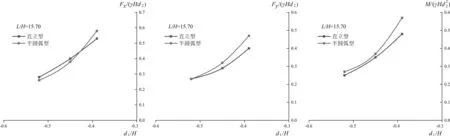
图13 直立型与半圆弧型挡浪墙所受水平波浪力比较曲线Fig.13 Comparison curve of horizontal wave forces on vertical and semicircular arc parapet wall图14 直立型与半圆弧型挡浪墙所受垂直波浪力比较曲线Fig.14 Comparison curve of vertical wave forces on vertical and semicircular arc parapet wall图15 直立型与半圆弧型挡浪墙所受波浪总力矩比较曲线Fig.15 Comparison curve of total wave moment of wave between vertical and semicircular arc parapet wall

(2)不同结构挡浪墙结构型式对其墙体承受波浪力的影响。

作用在半圆弧型挡浪墙上的波浪力和波浪总力矩随着墙前相对水深d1/H、波坦L/H变化与直立型挡浪墙具有相同的变化规律(图13～图15)。由于半圆弧型挡浪墙所具有的挑浪作用，虽能减少墙顶越浪量，但其所受的波浪力要大于直立型挡浪墙。当墙前相对水深d1/H较大时，半圆弧型挡浪墙所受到的水平波浪力、垂直波浪力以及总波浪力矩比直立型挡浪墙都要大很多(当波坦为15.70，墙前相对水深为-0.39时，半圆弧型挡浪墙所受到的水平波浪力、垂直波浪力以及总波浪力矩分别为0.58、0.47、0.57，直立型挡浪墙分别为0.53、0.40、0.48，增大幅度为10%～19%)。由此可知若直立型挡浪墙墙顶越浪量较大时，可采用半圆弧挡浪墙减小墙顶越浪量，由于半圆弧挡浪墙受波浪力及倾覆力矩都大于直立型挡浪墙则需要考虑提高半圆弧挡浪墙整体稳定性。

(3)斜坡堤坡比变化对直立式挡浪墙墙体承受波浪力的影响。

作用在1:2.5坡比海堤设计断面挡浪墙上的波浪力和波浪力矩随着墙前相对水深d1/H与波坦L/H变化与1:2坡比海堤挡浪墙具有类似的规律(图16～图18)。坡比变化时对直立式挡浪墙墙体承受波浪力的差别在于：墙前相对水深d1/H<-0.45时，1:2.5坡比海堤断面挡浪墙所受到的水平波浪力(0.24)、垂直波浪力(0.22)以及总波浪力矩(0.23)大于1:2坡比海堤断面挡浪墙(0.23、0.20、0.21增大幅度为5%～10%)。

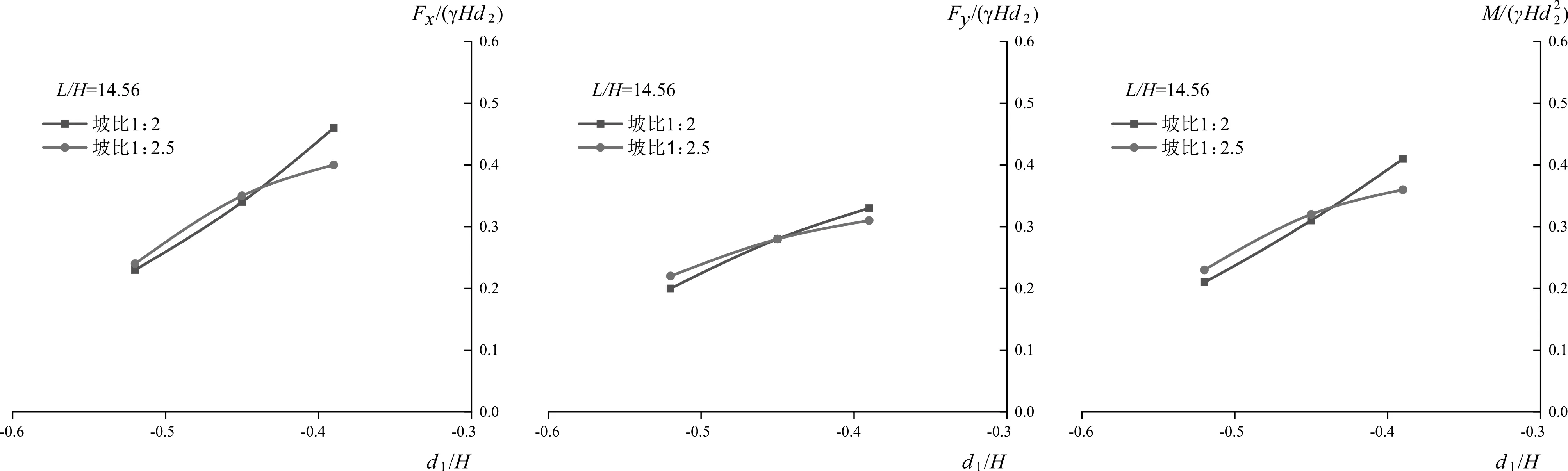
图16 坡比1:2与1:2.5海堤挡浪墙所受水平波浪力比较曲线Fig.16 Comparison curve of horizontal wave force on slope sea dike parapet wall between 1:2 and 1:2.5图17 坡比1:2与1:2.5海堤挡浪墙所受垂直波浪力比较曲线Fig.17 Comparison curve of vertical wave force on slope sea dike parapet wall between 1:2 and 1:2.5图18 坡比1:2与1:2.5海堤挡浪墙所受波浪总力矩比较曲线Fig.18 Comparison curve of wave total moment on slope sea dike parapet wall between 1:2 and 1:2.5

5 结论

采用Fluent软件构建数值波浪水槽，计算与研究斜坡式海堤堤顶直立型和半圆弧型挡浪墙随斜坡坡比、水深、波高、波周期等参数变化对其承受波浪力的规律及特性，结论为：

(1)墙前相对水深d1/H<0时，挡浪墙迎浪面各测点的波压力总体随堤前水深、入射波波高及波周期增大而增大，呈近似的线性特点。2种型式的挡浪墙所受水平与垂直波浪力、总波浪力矩都随着墙前相对水深d1/H、波坦L/H的增大而增大。

(2)相同波要素且斜坡坡比m=2.0时，半圆弧型挡浪墙较直立型挡浪墙具有挑浪作用则其所受波浪力值大，增大幅度为10%～19%，且波浪力值随墙前相对水深增加而增大。

(3)在波坦L/H从13.08到15.70的变化范围内，为提高挡浪墙的稳定性，降低波浪力及倾覆力矩，可增加挡浪墙底板宽度。

(4)相同波要素条件下，较大的斜坡坡比(m=2.5)可能导致海堤断面挡浪墙所受波浪力较大，在墙前相对水深d1/H=-0.52～-0.39、波坦L/H=13.08～15.70的变化范围，当墙前相对水深d1/H<-0.45时，宜采用坡比1:2.0，反之采用坡比1:2.5。

(5)考虑降低墙顶越浪量，应取半圆弧型挡浪墙型式。