面向多核处理器的机器学习推理框架
张 潇 支 天
1(中国科学院计算技术研究所 北京 100190)2(中国科学院大学 北京 100049)3(上海寒武纪信息科技有限公司 上海 201306)
近年来,得益于深度学习技术在多个领域取得的巨大成功[1-6],包括图像识别、物体检测、语音识别和文本处理等,深度学习已经成为了目前最为火热的研究领域.除了针对深度学习模型和算法的研究之外,研究人员同样也在探索如何使用能够更加高效地执行这些深度学习模型和算法,GPU是目前最为主流的深度学习计算平台,被广泛应用于深度学习领域的云服务中.此外,专用的深度学习处理器[7-11]也成为了快速发展的一个领域.专用处理器针对神经网络算法的计算特点设计其本身的硬件结构,使其更加符合算法的计算逻辑,因此专用处理器往往在性能功耗比上对比GPU有较大的优势.虽然出现了包括GPU和专用加速器在内的这些新型硬件,通用处理器仍然是目前最为普遍且易于得到的计算设备.随着技术的发展,基于内存共享模型的多核处理器已经成为了当前处理器的主流架构,这种多核架构和每个核内的向量处理能力同样可以运用到神经网络计算中.考虑到计算资源的易获得性,探索多核处理器在神经网络计算中的高效应用同样有着重要的意义.基于共享存储模式设计的多核处理器在训练场景下可以使用数据并行的方式方便地扩展自己的数据吞吐量.所谓数据并行指的是通过把训练的数据集划分成若干份,使用多个处理核分别处理一部分子数据集来加快训练.在多核结构中采用这种方式,每个核并行地处理训练数据中的不同数据集,从而提高整个系统的吞吐量,加快训练速度.因此,多核的处理器架构在保持了每个核良好的性能功耗比的前提下,又可以方便地扩展整个系统在训练阶段的计算吞吐量.
在实际应用中,当在线下使用数据集完成了神经网络模型的训练后,就会把模型部署到云端的服务器上来处理外界发来的数据,此时的应用场景就由离线训练变成了在线推理.在在线推理阶段,一个非常重要的指标是时延,也就是从服务器端收到待处理数据到返回处理后的结果的时间,进一步来说,是使用神经网络模型处理数据的时间.低时延能够保证云端服务器对客户端发来的数据在最短的时间内做出响应,在一些更加敏感的场景下,直接决定了方案是否可用.因此,在线推理阶段对于处理器的要求就由处理大批量数据、高吞吐量转变为处理小批量数据、低时延.
在这种情况下,传统的数据并行或者模型并行难以有效降低推理任务的时延.对于数据并行来说,大批量数据是并行加速的前提,而这与在线推理小批量数据的特点相矛盾.对于模型并行来说,它通常是为了解决一个规模很大的神经网络模型超过了单个设备的内存限制而采用的方法,把算子分配到不同的核上并不能降低网络的时延.所以为了能够在多核处理器上降低执行推理任务的时延,必须寻找一种方法,把对小批量数据甚至单个数据的推理计算任务的负载合理地分配到多核架构的各个核上,保证每一时刻都有尽可能多的核参与计算,才能充分利用多核架构的资源.一种直观的方法是把神经网络中的每个算子的计算任务都拆分到多个核上计算,这种方法即使在处理单张图片的推理任务时也能保证每一时刻都有多个核参与计算,从而达到利用多核资源降低时延的目的.
但是,对于多核处理器来说,还有很多要解决的问题.首先,处理器往往需要足够的数据规模才能达到较高的计算效率,而算子内的进一步拆分会减小每个核上的计算规模.当拆分达到一定粒度,每个核上计算效率的损失会超过拆分增加并行度所带来的收益.因此,必须在拆分并行和计算效率之间进行平衡,在保证足够计算效率的同时提供足够的并行度.另一方面,神经网络模型可以看做是一个由通常数以百计甚至千计的算子所构成的复杂计算图.不同种类的算子内的算法逻辑各不相同,这就导致对这些算子进行拆分的方法也不一样.每个算子的拆分,除了平衡自身的计算效率和并行度,还要考虑和前后算子的搭配,甚至于对全局的影响.深度学习的快速发展带来的是越来越多的大规模复杂网络,通过手动方式寻找一种好的并行方法是不现实的,因此需要一种自动化的方法来保证对于不同的网络都能够给出一种较好的拆分并行策略.此外,还需要考虑的是对于底层处理器的可移植性.当我们把算子的计算任务均摊到多个核上时,通常来说,我们需要重新实现一个在多个核上执行的算子核函数,由单核扩展到多核,并且实现算子内部的拆分并行所带来的修改软件栈的工作量是非常大的.传统的数据并行和模型并行的实现仍然是基于一个处理核完成一个算子的计算任务,所以并不会带来很多额外的工作,而单个算子的跨核并行需要对算子本身的实现进行修改,这种修改的难易程度依赖于处理器的可编程性和原有算子实现逻辑的复杂程度.因此,如何减小在多核架构上实现低时延推理过程中的额外开销,使得方法能够在未来对于不同的多核处理器都有一定的通用性,也是一个需要考虑的问题.
针对上述问题,本文提出了一套完整的面向多核处理器低时延推理的框架设计,能够结合处理器自身的特点,针对不同网络自动生成一套较优的并行方案.
1) 针对多核处理器执行推理任务,提出了一种基于算子拆分的并行框架.框架定义了一套描述不同算子拆分的统一表述.通过描述神经网络计算图中数据的拆分方式,确定各种不同算子的拆分方案.
2) 把神经网络算子间的上下文衔接部分进行抽象并归纳成若干辅助算子.通过引入辅助算子的方式,衔接算子的单核实现与框架的多核拆分,减小了框架在处理器上的移植难度,使其在设计上能更好地支持未来更多的众核处理器.
3) 设计并实现了一套自动化方法,能够针对不同神经网络给出一套完整的端到端的拆分方案.在分析过程中,考虑了算子之间的衔接以及对于整个网络时延所造成的影响.
1 相关工作
1.1 数据并行
数据并行是目前大规模神经网络并行训练中最常使用的方法,最早可以追溯到2012年Google的DistBelief项目[12].DistBelief是Google大脑团队建立的第一代专用学习系统,它使用大规模的CPU集群进行神经网络模型的训练.数据并行的核心是使用多个处理器同时进行对于同一个神经网络模型的训练.在训练的每一轮迭代中,每个处理器从数据集中获取本轮迭代使用的数据,在处理器上完成一轮整个网络的推理及训练计算,并返回本轮计算得到的梯度数据来进行模型的更新.维护权值的服务器在收到所有处理器的梯度后,使用这些梯度进行模型数据的更新.显然,由于多个处理器会并行地执行训练任务,其等价于在每轮迭代中一个更大批量的数据能够被处理,也就加快了系统完成整个训练任务所需要的时间.所以,数据并行的关键在于每一轮迭代中待处理数据的批量大小,批量越大,就可以划分到越多的处理器上来并行处理.Facebook在2017年的工作[13]以及腾讯2018年的工作[14]通过多GPU数据并行的方式,实现了在短时间内使用海量图像数据集完成大规模神经网络网络的训练.
1.2 多核处理器
当前多核处理器采用的最普遍的结构是基于存储共享的多核结构,处理器中包含了多个计算核,每个计算核上有独立的缓存、寄存器堆、计算单元以及指令控制单元,所有的计算核共享同一全局存储,如图1所示.单个核已经足够完成任何复杂逻辑的计算任务,但其性能受限于摩尔定律和芯片工艺.为了进一步提升处理器的性能,多个计算核被引入处理器中,它们可以被用于处理那些有着较高并行度的计算任务.这种共享存储多核结构是一种经典的多核结构,并且非常适合数据并行的神经网络训练方法.每个核可以作为数据并行中的一个处理器,分别读取不同的数据然后并行完成网络模型的正反向计算.每个核在计算阶段仍能够保持其在之前单核架构下良好的性能功耗比,与此同时整个系统的吞吐量也可以随着核数的扩展而增加.数据并行的问题在于,其扩展性依赖于处理的数据批量的大小.尽管在训练阶段这通常不会是一个问题,但是对于推理阶段这个前提则难以保证.一般来说,用于实时服务领域(包括视频监控、自动驾驶等)的神经网络模型,处理的数据通常是以流的方式串行输入,导致了每次处理的数据规模很小甚至往往是单张图片.在这种情况下,数据并行不能提供任何并行度,所有的工作任务会集中在单个核上,这使得多核带来的计算资源不能转化成处理任务的速度.
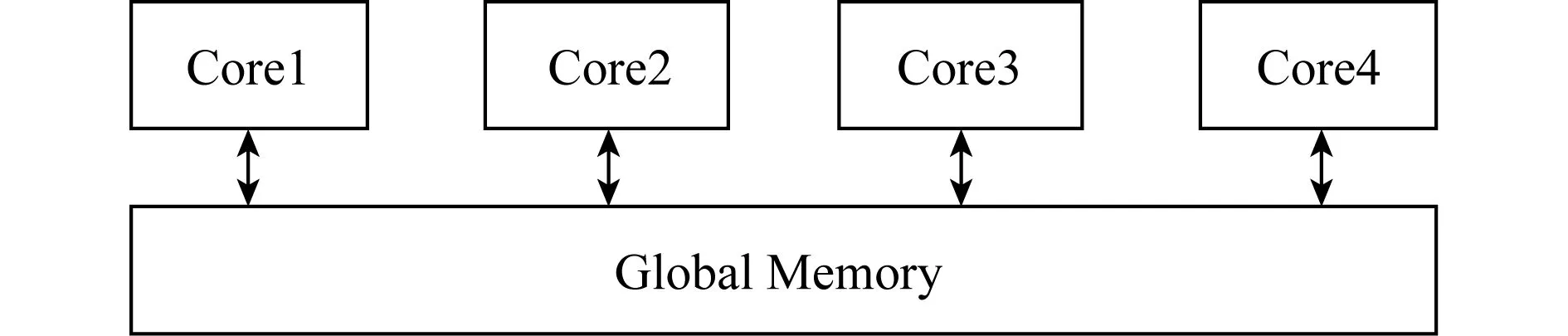
Fig. 1 Multi-core shared memory architecture图1 共享存储的多核结构
1.3 基于模型拆分的多核并行
Zlateski在2015年提出了一套在内存共享多核机器上进行卷积神经网络训练的框架ZNN[15].该方法的主要过程是把卷积神经网络的计算任务拆分,通过在多个核上调度执行拆分后的子任务,实现在多核结构上加速卷积神经网络的计算.对卷积计算来说,输入数据和输出数据可以分别看作是一个三维甚至更高维度的张量,其中C维度表示特征图像的数量. ZNN在拆分网络中的卷积算子时,把计算任务在输入数据的特征图像维度和输出数据的C维度上进行拆分,拆分成粒度为1的子任务.如图2所示,每个节点表示所处的张量在C维度上粒度为1的一份子数据,实线箭头表示卷积计算,虚线箭头表示池化计算.可以看到,如果模型本身在C维度上足够宽,就可以获得足够数量的子任务进行并行计算.
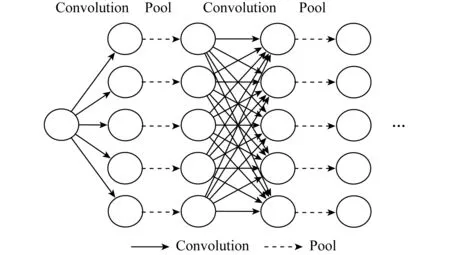
Fig. 2 Strategy in ZNN to split convolution networks图2 ZNN拆分卷积神经网络的方法
尽管如此,ZNN在任务拆分阶段的实现过于简单,更多地考虑如何对拆分后的子任务进行调度和同步.这种把卷积和其他算子在C维度上拆分到1的细粒度的拆分适合于处理器上没有经过任何优化的简单实现,但是对于利用向量计算能力并且经过高度优化的计算任务来说并不可行.正如1.1节所述,处理器需要足够的计算规模来保证计算效率,这种特征图像尺度为1的计算任务在处理器上执行时很难达到较好的计算效率.此外ZNN主要用来加速卷积神经网络模型,其能够处理的算子主要有卷积,池化和通用的对位计算算子.虽然这3种算子是卷积神经网络中最常用的算子,但用来处理其他包含更多特殊算子且结构更加复杂的网络时却远远不够,这限制了ZNN本身的泛用性.
2 算子拆分及其表达方式
本节将介绍如何在多核处理器上对算子进行拆分,以及使用一套统一的表达方式来表示对整个网络的拆分策略,此外将说明框架为了可移植性所引入的辅助算子.
2.1 算子拆分
我们的出发点是希望把一个算子拆分成多个规模更小的子算子,这样可以直接调用单核架构下的计算库,避免了重新实现的额外工作量.比如,一个激活算子在经过拆分后可以得到许多更小的激活算子,这意味着我们只需要在多个核上调用原有的单核版本的激活算子完成每个子任务,而不需要修改或者重新实现一个多核版本的激活算子.
卷积算子是一个最值得关注的算子.在ZNN中,作者在卷积层的输入输出数据的C维度上进行拆分, 而处理器往往需要一定规模的数据才能保证得到较高的计算效率.当前处理器普遍提供了向量处理指令来处理器长位宽的向量计算.如果计算的维度过小以致于无法填满向量计算的位宽,就会导致计算单元被浪费,对核上的计算效率造成很大的影响.在同样的拆分数情况下,同时在输入和输出C维度上均衡拆分的加速比优于在单个C维度上过度拆分的加速比.显然,应该尽量避免C维度上的过度拆分来保证计算效率,但同时又需要足够的拆分数量来保证多核上的计算资源可以被充分利用.我们使用N和C来表示卷积算子输入输出张量的前2个维度,维度的数值分别代表批量的大小、特征图像的个数,则框架对于卷积算子的不同方式的拆分可以描述成以下3种,3种情况可以相互交叉、同时存在,保证了足够的拆分度:
1) 当卷积算子输入数据的N维度超过1时,对N维度上进行拆分;
2) 在卷积算子的输入数据的C维度上进行拆分;
3) 在卷积算子的输出数据的C维度上进行拆分.
如图3所示,3种拆分都是把原始的卷积算子拆分成更小的卷积.其中,图3(a)是把1个数据批量为2的卷积算子拆分为2个输入批量为1的卷积算子;图3(b)是把1个输入数据特征图像个数为4的卷积算子拆分为2个输入数据特征图像为2的卷积算子;图3(c)是把1个输出数据特征图像个数为4的卷积算子拆分为2个输出数据特征图像为2的卷积算子.此外,虽然图3(a)中对N维度的拆分在小批量输入甚至单张图像的推理任务中似乎没有必要性,但实际上目前深度学习领域新出现的网络结构和算法已经逐渐模糊各个数据维度的物理意义和彼此之间的界限.例如,何凯明等人于2017年提出的目标实例分割网络Mask R-CNN[16]中,即使在处理单张图片的情况下,网络中的部分卷积算子和全连接算子在N维度上会扩展到1 000的规模.因此,支持算子在N维度下的拆分有利于框架去更好地处理未来新的网络结构.
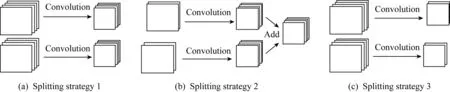
Fig. 3 Different splitting strategies on convolution operation图3 卷积算子的不同拆分策略
根据卷积算子的特性,我们引入了3种拆分策略,而对于其他种类的算子,根据其计算特性的不同,同样有不同的拆分策略.为了能够统一地表达所有这些算子的拆分策略,我们使用算子的输入输出数据的拆分来表示算子本身计算逻辑的拆分,即通过描述与算子相关联的输入输出数据被划分成怎样的子块来说明该算子在计算上是如何分成更小的子算子的.例如,当全连接算子的输入数据在C维度上被分成了更小的子块,则说明该全连接算子本身的计算在输入C维度上被分成了多个输入C维度更小的全连接算子.同样地,输出数据如果在C维度进行到了拆分,则说明算子在输出神经元的维度上被拆成了更小的全连接算子.
更加具体地说,当一个激活算子的输入数据被分成了若干个子块(从一致性的角度来考虑,输出输入也会进行同样的划分),不妨表示为input0,input1,…,inputm-1和output0,output1,…,outputm-1,则在计算阶段,整个激活算子实际上被拆分成了m个更小的激活算子,这些激活算子彼此之间没有依赖关系,可以运行在多个核上.而如果激活算子的输入数据没有做任何拆分,这代表该算子不会被划分成更小的子算子,那么在执行阶段只会在单个核上进行计算.这种方法可以简单明确地说明算子本身是如何被进一步拆解的,根据我们的实践经验,目前为止所有算子都可以用这种方式来表示其拆分方式.
2.2 调整数据的拆分形式
对于单个算子来说,我们可以通过实验来得到其最佳的并行策略,拆分策略的枚举空间包括:
1) 并行度.即该算子将被拆分成多少个子算子.这一变量通常受限于多核架构的核数,在不超过核数上限的前提下可以采用2的幂次.
2) 拆分维度.即算子应该采用怎样的方式来划分子算子.这一点对于那些对拆分方式性能非常敏感的算子是有意义的.
3) 拆分维度大小.即在决定了拆分维度之后,还需要确定每个维度上拆分的数量.一般来说,各个维度上拆分数量的乘积即是该算子的并行度.
以上3点在一起表示单个算子拆分策略的搜索空间,对每一个算子的每一种特定规模,我们采用枚举的方式遍历该搜索空间中的每一种拆分策略得到其实际的性能,从中我们可以得到一个性能最优的拆分策略,它代表了在该计算规模下的算子在该底层处理器上所能得到的最好性能.
我们使用数据的拆分来表示算子本身的拆分,这使得算子本身的拆分会影响与其相关联的数据,而不同算子对同一数据的影响在整个网络中应当是一致的.举例来说,上下相邻的2个算子op1和op2,op1的输出数据即是op2的输入数据,当op1采用某种拆分策略stg1时,对应的其输出数据有拆分格式l1,与此同时,op2采用拆分策略stg2时会导致其输入数据有l2.l1和l2实际上是对同一数据的拆分格式的描述,两者应该保持一致.因此,当op1已经给定了其输出数据的拆分l1时,op2的拆分方式在某种程度上也同样被决定了.这是一种非常糟糕的限制,因为神经网络每一层的算子的类型和规模通常都是不一样的,这意味着对不同的算子来说,其最佳的拆分方式也是不同的.另一方面,目前网络中算子的种类繁多,不同种类的算子支持的拆分策略也是不同的.部分算子可能只支持在有限维度上进行拆分,甚至由于计算逻辑过于复杂而完全不支持拆分,这使得网络中每个算子的拆分方式取决于所有这些算子所允许的拆分方式的交集.在最糟糕的情况下,倘若网络中含有不支持任何形式拆分的算子,网络中的其他所有算子为了在数据的拆分格式上保证一致性,都需要采用不拆分的策略.
为了解决这个问题,框架引入了调整算子,来保证网络中的每一个算子都可以自由地选择适合自身的拆分策略.调整算子用来把数据张量按照某种方式拆分得到的子数据块调整成按照另一种拆分方式得到的子数据块.通过在每个算子和其输入数据之间插入调整算子,让网络中的每个算子都可以不受外界约束地选择恰当的拆分策略.具体来说,对于由前后相邻的算子op1和op2所构成的序列,在op1的输出(也即op2的输入)和op2之间插入调整算子,这样op1的输出可以经由调整算子转换成另一种拆分格式,因而op2的拆分策略的选择将不会再受到op1的限制.
2.3 补偿算子
根据算子计算输出数据块C维度上的一个值所需要的在输入数据块C维度上数据的范围,可以把算子归纳为3类:1)点对点的算子.即计算输出张量的一个点只需要输入张量上与之对应的一个点的值,这一类算子包括激活算子(Relu,pRelu)、批标准化算子(BatchNorm)以及对位加减乘除的基本算子(Add,Sub,Mult,Div).2)全依赖类型的算子.即计算输出张量的一个点只需要输入张量上在对应C维度上的所有数据,例如归一化指数回归算子(Softmax),其计算逻辑使得我们很难在归一化的维度上对计算进行拆分.3)区域依赖类型的算子.即计算输出张量上的一个点需要输入张量在对应位置附近C维度上的数据,例如LRN算子的C维度.
对于属于第1种情况的算子,我们可以在C维度上进行任意拆分.对于属于第2种情况的算子,在相应维度上基本不能拆分.而对于属于第3种情况的算子,我们通过引入补偿算子来保证C维度上的可拆分性.补偿算子用来把一个子数据块之外的相邻数据从其他数据块的存储位置读取过来,和原本的数据合并在一起形成新的数据块,这样可以保证每个子算子所需要的数据一定位于其所对应的输入数据块中.
3 基于整个网络的拆分决策
本节将具体说明怎样基于网络本身的特点和底层处理器的计算规律,针对大规模的神经网络模型自动给出一套端到端的拆分方案,在这个过程中,既需要兼顾每个算子本身拆分后的计算效率和并行度,也要考虑上下文算子彼此之间在拆分上的相互配合.最终目标是得到一个能够有效降低整个神经网络模型端到端的推理时延的拆分并行方案.
3.1 张量数据的状态空间
神经网络模型通常可以看作是一个由算子和多维张量数据所构成的有向无环图,算子和数据彼此之间通过有向边相互连接,有向边的指向表明了数据是算子的输入或者是输出.使用op表示算子,tensor表示张量数据.同时,第2节已经说明,为了统一不同算子的拆分方式的表达,框架统一选择使用与算子相关联的张量数据的拆分方式来说明算子本身的拆分方式.不妨假设网络中所有张量数据都是4维的,对于实际维度不到4的数据(例如图像分类网络最后的全连接层和归一化指数回归层的输入输出),可以将其表示为低纬度为1的4维张量.对于框架本身来说,可以支持含有任意维度数量的张量数据的神经网络模型的处理,尽管如此,4维对于相当大一部分的神经网络结构都足够使用.
把张量数据的任意一种拆分称为该张量数据的一种状态s,所有可能的拆分{s0,s1,s2,…}组成了该张量数据的状态集合S.一般来说,这是一个非常大的状态空间,意味着由张量的状态所表示的算子的可能拆分方式的空间同样也非常巨大.通过一些合理的假设,可以对张量数据的状态空间进行剪枝.首先,多核处理器完成一个算子的计算时延取决于执行子任务耗时最长的那个核的时间,而多核架构中各个核在硬件结构上彼此是相互对等的,因此每个核的时间耗费的长短取决于分配给该核的任务负载的多少.所以一个合理的假设是应该保证拆分后的子算子的规模大致均衡,为此,可以从张量的状态空间S中省去那些拆分上不均衡的状态.此外,多核架构中核数通常是2的整数次幂,如1,2,4,8,16等,一个并行度不是2的整数次幂的任务往往会导致在核的调度过程中产生“碎片”,因此拆分后的子算子数量应当保证是2的整数次幂.通过这2个假设,可以极大地缩小算子拆分策略的搜索空间.
3.2 基本原理
把一个包含n个算子的串行神经网络模型描述成一个算子序列(op1,op2,…,opn),假设每个算子只有一个输入和一个输出,前一个算子的输入是后一个算子的输出,那么包括整个网络的输入数据张量和输出数据张量以及算子之间的中间结果张量在内,所有的张量构成集合{tensor0,tensor1,…,tensorn},opi的输入是tensori-1,输出是tensori.对每个数据张量tensori,有与之对应的状态集合Si,搜索策略的目标是寻找一种张量本身和其状态集合的某个状态之间的映射关系tensori→si,通过给神经网络模型中每个张量确定一个具体的状态,从而可以确定所有算子的拆分方式,因此,把一个神经网络中所有数据到其状态的一种映射关系称为该网络的一种拆分方案P.在计算阶段,第i个算子opi以处于拆分状态s的输入数据计算出处于拆分状态r的输出数据,具体的并行计算方式由输入数据和输出数据的状态所决定,同时,该算子的计算时间记为ts→r,其值的大小取决于相应的拆分方式和底层处理器的硬件特性,则整个网络的时延T计算为
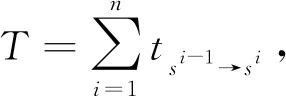
(1)
其中si∈Si.
整个网络的拆分方案P可以看作是由每个算子的输入张量的状态集合中的一种状态向输出张量中的一种状态的跳转.前一个算子的输出张量的拆分状态即是后一个算子输入张量的拆分状态.不同的数据张量的状态集合是不同的,同时跳转前后的2种状态也可能不同.经过算子的每一种可能的跳转对应了在该算子上的一种有效的拆分方式,同样与之对应的还有使用该拆分方式在多核处理器上并行执行该算子所使用的时间ti,因此ti可以被看作是由算子的输入张量的状态指向输出张量的状态的有向边的权重.同时,作为整个网络的输入张量和输出张量,它们对应的状态空间中只有唯一一种不拆分的状态,这使得神经网络的拆分方案P由完整的输入数据开始到完成的输出数据结束,外部的用户始终看到一个完整的输入和输出.此时,对于给定的神经网络模型搜索一个好的拆分方案P,即是寻找一条由输入张量的不拆分状态到输出张量的不拆分状态的最短路径,该路径在每个中间结果张量的有效状态空间中都要选择一个状态经过.这种抽象的公式表示为
P={s0,s1,…,sn}=arg min(T(s0,s1,…,sn)),
(2)
(3)
在单个算子的性能优化阶段,我们可以采用枚举的方式遍历来获得单个算子所有可能的拆分策略对应的性能,从中得到其在处理器上最优的策略,但对于整个网络来说,采用枚举遍历的方式来求解最优的拆分策略是非常不合适的,因为潜在的搜索空间非常巨大.不妨假设整个网络中算子数量为N,而每个算子可选择的拆分策略的个数为P,则整个网络可供搜索的拆分策略的数量是PN,考虑到目前的大规模神经网络往往有数以百计甚至千计的算子,而P通常会在十几到几十之间,穷举所有待选择的方案从时间和资源上来说都是不现实的.为此,我们采用一种机器学习的方法来帮助系统进行决策.

Fig. 4 Architecture of decision-making system for networks partition图4 算子拆分决策系统的结构
从问题的本质上来看,对于网络中的每一个数据,都要求给出该数据的一种拆分状态,所有这些拆分状态组合在一起就构成了整个网络的一种拆分方案P.数据之间通过算子相互关联起来,每个数据的拆分都受限于其上和其下的算子,因此问题的本质是基于数据的前后上下文信息对数据本身的拆分方式进行决策.考虑到问题本身的特性,我们采用基于注意力机制的循环神经网络来处理这个问题.网络的输入是包含所有数据及其相关信息的特征向量组,输出是每个算子的拆分选择.从随机生成的拆分策略开始,每一轮根据上一轮生成的拆分策略在设备上实际执行的时间来更新模型,使用更新后的模型进入下一轮,整个过程由一轮一轮的“更新-测试”过程组成,直至得到一个针对当前模型较好的拆分策略.如图4所示,网络被视作是一个由数据通过算子连接所构成的图结构,信息嵌入模块(embedding module)把图4中的每个数据抽象成对应的特征向量,里面既包括了数据本身的形状大小,也包括了该数据前后的算子的类型以及其他相关信息.数据之间的连接关系,也就是网络的图结构同样被嵌入每个数据块的特征向量中,通过在特征向量中引入与当前数据有直接连接关系的其他数据的标号,从而描述了整个网络的图结构信息.网络中所有数据块的特征向量被作为输入信息,而输出则是每个数据块对应的拆分方式,即数据在每个维度上拆分的段数.图4中循环神经网络中每一个输出单元输出的是对应的数据选择不同拆分策略的概率大小,我们依据该概率分布,使用采样的方法从中得到一种拆分策略并执行每一轮中进行n次采样,每次采样可以得到一套包含所有数据拆分方式的完整的全网络拆分方案,我们使用n个方案的执行时间来更新决策模型,即循环神经网络中的参数.
在使用循环神经网络的决策模型得到待拆分网络的拆分方案后,并不能直接执行该方案来得到相应的执行时间.如3.1节中所述,网络的拆分方案由网络中每个数据块的拆分方式来决定,而每个数据块的拆分方式,不单单需要明确数据块在各个维度上的拆分份数,同样也需要明确每个维度上每一子段的起点和终点.例如对形如(0,n),(0,c),…的数据块,在明确其会在C维度上拆分成2份后,还需要明确每一份的起止点分别是什么,即给出这样的形式(0,n),((0,c1),(c1,c)),….因此,图4在循环神经网络结束后,使用推理模块(inference module)对网络中所有数据块的具体拆分形式进行推理.对于整个网络的输入数据,按照循环神经网络的输出所提供的策略,对输入数据进行尽可能均等的拆分,而对于网络中的其他数据块,则依照循环神经网络的输出所提供的策略,同时按照网络中算子的计算逻辑,由输入数据的具体拆分形式推导出输出数据的具体拆分形式.
3.3 减小决策空间
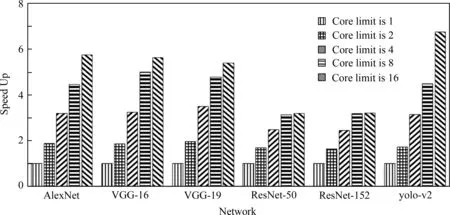
Fig. 5 Speed up of different networks with different core limits图5 不同网络在不同核数上限下的加速比
算子融合(kernel fusion)是当前神经网络优化中常用到的一种技术.传统的GPU或者CPU上的神经网络优化往往针对每个算子内部的计算逻辑,通过增加向量化,提高片上存储的利用率来提高单个算子的执行性能.这些优化受限于算子本身所能提供的优化空间,会有一定的局限性,而算子融合则是通过把神经网络中的多个算子融合成一个新的算子,这种融合打破了算子与算子之间的隔阂,一方面可以减少每个算子启动(kernel launch)的开销,另一方面可以省去一些不必要的算子之间中间结果的访存开销.最常用的算子融合的情况是把卷积、池化或者其他别的常用算子与其之后的若干个连续对位计算算子合并成一个新的算子.对位计算算子泛指一类神经网络中常见的算子,其特点是输入数据和输出数据有着相同的形状,且计算输出数据中一个数值只需要输入数据中与其相对应的位置上的数值,这样的算子包括Relu和其他激活算子Scale,BatchNorm等.通过把对位计算算子和其前面的任意算子进行融合,可以避免中间结果的访存开销.序列最前端的非对位计算算子在计算过程中,每计算出一个点的数值,可以立即对该数值进行后续的对位计算,从而得到整个算子序列的最终结果,而不是把当前的输出存至存储中,再由后续的对位计算算子重新从存储中读回再进行计算.
为了减少网络中数据块的数量,从而减少待决策空间的大小,加快每个网络的训练决策速度,在这个决策过程开始前,会对待拆分的神经网络模型进行预处理.在预处理过程中,对位计算算子将会被合入其前面的算子中,相应地,算子之间的中间结果也会从计算图中被移除,因为此时这些数据已经成为了算子内部的临时数据.这种合并可以有效减少整个网络中数据块的数量,缩小待决策空间.另一方面,这种方法保证了在最终得到的拆分方案中,对位计算算子的拆分方式始终与其输入数据保持一致,从而确保在拆分后得到的计算图中这些子对位计算算子同样可以使用算子融合的方式进行优化.
4 实验与结果
本节将检验基于算子拆分的多核并行框架对于小批量数据推理任务的时延的提升效果.实验平台是Intel Xeon E5-2666 v3处理器,有18个核,主频2.9 GHz.由于框架中拆分数量采用2的整数次幂,因此最高的有效核上限为16.算子实现上采用Intel的深度学习高性能计算库MKL-DNN.我们选择图像分类网络AlexNet[4],VGG-16[17],VGG-19[17],ResNet-50[18],ResNet-152[18]以及物体检测网络yolo-v2[19]作为测试集,测试这些网络给定不同最大核数上限的条件下的单张图片推理时延的相对加速比,测试集中的网络被广泛应用于计算机视觉领域中.图5中的测试结果显示,不同的神经网络模型在经过框架的拆分并行处理后,可以得到3x~6x不等的性能提升,其中VGG网络和yolo-v2分别达到 5.6x和6.7x的性能提升.由于底层多核处理器的带宽限制,大部分网络在核数上限由8变成16的阶段的性能提升已经趋于平缓.考虑到在真实应用场景下,网络处理的通常是1 920×1 080的高分辨率图像,图6给出了处理大尺寸图像时网络在不同核数上限下的加速比.可以发现,不同类型的网络此时的相对比相比于小尺寸图像做输入时明显提升,由3x~6x不等变成5x~8x不等.这是因为输入图像尺寸规模的增大使得网络中所有算子的计算规模增大,有助于减缓每个核计算效率随着拆分数量增大的衰减速率,因此在同样拆分模式下,每个子算子在计算阶段可以获得相比于处理小尺寸图像时更高的计算效率.
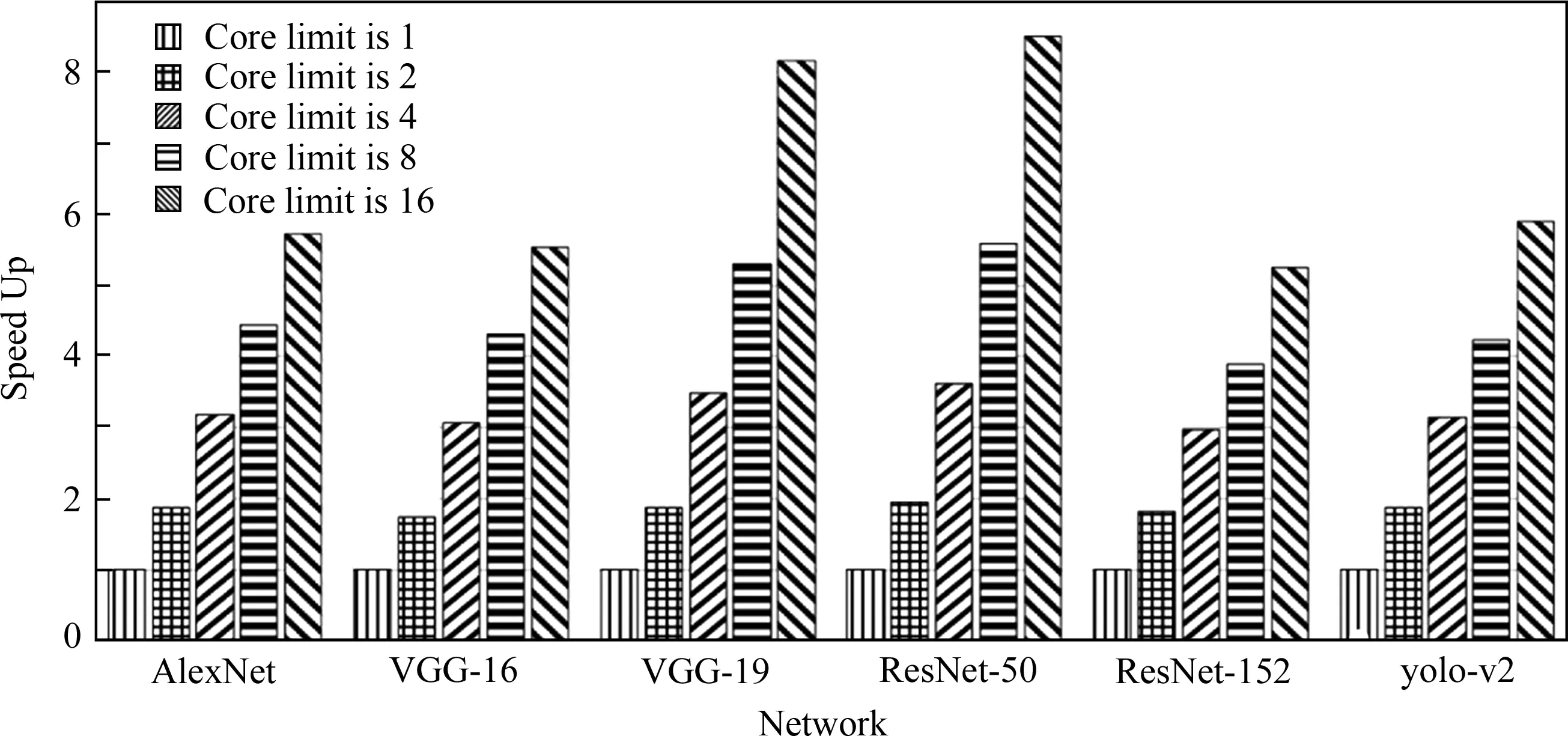
Fig. 6 Speed up of different networks with different core limits when processing 1 920×1 080 input image图6 不同网络处理1 920×1 080的输入在不同核数上限下的加速比
5 总 结
在本文中,我们设计并实现了一套面向多核处理器的低时延机器学习推理框架.框架通过把神经网络中的每个算子拆分成更小的子任务分配到多个核上并行执行来充分利用多核系统的硬件资源.通过引入少量的辅助算子,保证了网络在拆分后的计算图仍然可以使用单核上的算子核函数来实现,避免了框架在移植过程中需要修改或者重新设计大量算子的软件实现,使框架在不同的处理器架构上更加易于移植.框架能够自动生成一套对于给定神经网络和多核处理器的高效拆分方案,在方案的生成过程中,能够根据单个算子的类型和规模结合底层硬件的计算吞吐速率和访存带宽合理调整单个算子的拆分方式,在硬件核的计算效率和算子的拆分度之间取得较好的平衡,同时也会兼顾上下文算子之间在拆分上的相互配合,统筹规划多个算子的拆分选择.实验结果表明,在该框架下,不同类型的神经网络处理小尺寸小批量数据时,其端到端时延性能可以提升3x~6x,而在处理高分辨率图像时,端到端时延性能可以提升5x~8x,这使得多核处理器能够更好地胜任小批量低延迟的神经网络推理工作,有利于其在云端更好地推广和使用.
同时也要指出,本文的方法建立在对每一个待拆分网络都需要离线训练拆分策略模型的基础上.虽然从结果上看最终得到了不错的拆分策略,但是离线且单独训练的方式只能适用于那些事先已知结构从而可以事先处理的网络模型.而对于从未见过的网络,必须重新训练相应的决策模型,所以不能立即给出网络的拆分方案.在未来的工作中,我们将把重点放在研究如何对事先未知的网络模型也能实时快速地给出拆分方案.实时地拆分各种结构的神经网络模型将有助于我们将该方法嵌入当下主流的深度学习框架中,优化其对于多核处理器的使用.

