自适应预测制导：一种统一的制导方法*

胡 军

0 引 言

各类航天器的发射控制、轨道控制与捕获、再入与着陆控制、以及载人航天应急救生控制等的共同特点是将航天器从初始位置、姿态，以一定的性能指标要求，导引到终端轨迹或终端位置与姿态，且满足过程中运动状态和控制的约束.研究一种既具有给定适应性和鲁棒性同时又能满足任务的终端指标、运动约束和控制约束的制导方法，是国际航天领域公认的技术难题，也是各国长期一直研究的重大基础性和关键性课题.

该问题的特点也是难点体现在：初始范围大、精度要求高(终端约束强)、控制能力受限(控制约束)、对过程中的运动状态有严格的约束，被控对象和运行环境的不确定性大.

航天器的制导方法主要分为两类：一类是跟踪标称轨迹的制导方法，另一类是预测校正制导方法[1].

标称轨迹制导方法基于参数不变和小偏差摄动假设，虽然离线参数选择和数学仿真的迭代设计工作量大，但实时制导的计算量小，简单可靠，在航天器制导技术发展初期，应用广泛，如二十世纪六十年代至九十年代设计的美国、俄罗斯(前苏联)、中国的载人飞船及众多航天器均采用标称轨迹制导方法，但该方法对初始条件的大偏差以及动力学参数较大的变化适应性差，甚至不稳定.飞行任务中需要满足使用条件才能保证标称轨迹制导方法的可靠应用.2010年以来，各航天大国均在新的航天计划中引入预测制导方法.

预测制导方法，要求每个制导周期，计算机在线求解从当前状态到终端状态的动力学方程，考虑终端状态、过程中的运动约束以及控制约束，给出制导修正量.轨迹预测制导方法相对标称轨迹制导方法实现复杂，实时制导的计算量大，但离线参数选择和数学仿真的迭代设计工作量小，对初始条件的大偏差以及动力学参数较大的变化适应能力强.

实时制导计算量大的主因是在线求解从当前状态到终端状态的动力学方程，一般不存在解析解；在一定假设条件下的分段近似解析解，不适应长航程轨迹，也不满足高精度的制导要求.一般的预测制导都是采取数值求解动力学方程进行预测.由于预测的终端误差、运动约束等与制导修正量之间的关系不清楚，直至目前，尚未找到制导修正量与终端误差以及运动约束之间的数学模型.求解制导修正量是预测制导的核心问题.

国外预测制导，普遍采用数值迭代方法，如NEWTON-RAPHSO或Gauss-Newton法，搜索优化；迭代的计算量大导致预测校正周期长，反过来不利于预测制导的精度；由于无法找到预测校正输入输出之间的数学模型，迭代算法存在不收敛的问题，这使得预测制导方法在国外一直没有应用.

作者采用增量式预测校正，将控制增量和预测误差的关系，看成一个时变动态系统的输入与输出，研究发现了标称工况下预测误差与控制增量的时变动态关系，见图1和 图2，时变动态增益函数的倒数分解为输入变换和输出变换，作用于控制增量和预测误差之间的时变动态系统，见图3，得到标称工况下动态增益为1 的控制系统.实际飞行中，飞行弹道、控制指令都是非标称的，动力学参数、环境参数也相对标称值变化，上述基于标称轨迹的变换，仍具有重要效果，它使得变换后的系统，时变动态增益的变化范围大幅减小，为预测制导所有具体的设计方法均创造了良好的实现条件.例如，以载人飞船直接式再入某条标称轨迹为例，从再入开始时刻到标称开伞时刻的0～550 s时间内，正/负增量动态增益从1820000/1650000非线性地减小到0，考虑到再入后期控制能力的丧失，幅值最小值限幅为1，取正/负增量动态增益平均值作为设计使用的动态增益.采用时变动态增益倒数作为输入输出变换后，新的系统，0～550 s的时变动态增益，最大最小态增益比值可约束在100以内，确实为所有预测制导方法的实现均创造了良好的条件.根据标称工况动态增益为1而实际情况动态增益不为1、变化很大且有界的特点，作者将动态增益变换后输入输出的关系用时变特征模型描述，采用全系数自适应控制的方法解决制导问题，形成自适应预测制导方法.与国内外普遍的迭代搜索方法不同，自适应预测制导的每个实时制导周期，仅进行一次自适应控制计算，依靠参数辨识和自适应控制的收敛性，保证整个自适应预测制导的收敛性.

自适应预测制导的部分结果最早发表于1998年宇航学报[1]，当时在标称时变动态增益变换后的预测制导模型中采用的是时变系数二阶特征模型.2011年，针对月地轨道跳跃式再入，杨鸣、张钊、董文强采用该方法，相对国外预测校正算法获得了更好的数学仿真试验效果，结合工程实际，给出以自适应预测制导为外环(制导周期N·Ts)、标称轨迹制导[5]为内环(制导周期Ts)的双环自适应制导方案[4，6-7].2014年4月作者在杨鸣等工作[4]的基础上，在对月地轨道跳跃式再入深入研究与仿真过程中，提出将自适应预测制导中[1]标称时变动态增益函数变换后的广义对象输入输出关系，即预测制导模型由时变系数二阶特征模型改为时变系数一阶特征模型，设计了相应的参数估计和自适应控制方案.相对原来的二阶特征模型，基于一阶特征模型的制导律最大误差包络减小了20～30%，至此形成了最终的嫦娥五号飞行试验器返回再入制导方案[6-7].作者的研究思路和方法，异于国内外其他预测制导方法，是一项具有原创性的独特技术.

考虑到上述自适应预测制导方法这一原创性成果还未系统地出现在文献中，本文将以尽可能少的篇幅对此方法做系统性介绍.第1节对自适应预测制导方法进行系统介绍，其中1.1、1.2、1.3节是本方法的核心，是必选项，1.4、1.5、1.7节是可选项，1.6节需要根据具体问题进行设计；第2节介绍实际应用、推广应用以及应用研究情况；第3节对制导学科进行展望.

1 自适应预测制导方法

预测制导是根据模型计算预测误差，进而求制导修正量(制导增量)，该修正量是一个从当前时刻至终端的方波函数，方波幅值就是制导修正量的数值.将对预测误差的修正均匀分布于当前时刻至终端的时间区间.与标称轨迹制导方法只根据当前运动状态与标称轨迹的差求取制导修正量(制导增量)相比，预测制导是全局性制导，控制指令更平稳，精度也更高.自适应预测制导与控制方法包括：自适应全数值轨迹预测方法，一种时变动态控制增益变换方法，一种一阶特征模型的自适应控制方法，自适应预测双环制导方法，内环标称轨迹自适应纵向和横向制导方法，以及约束预判与制导处理方法等.

1.1 自适应轨迹预测[1-2]

预测制导的基础和前提是轨迹预测.

作者的研究表明，无论标称轨迹制导方法还是轨迹预测制导方法，在动力学与环境参数大偏差情况下，都会产生很大误差，这是由动力学内在机理导致的.对动力学和环境参数进行估计并进行自适应补偿，是解决偏差问题的有效手段.由于标称轨迹制导方法固有的以参数小偏差为假设前提，对标称轨迹制导方法自适应补偿的效果在程度上远不如对轨迹预测制导方法自适应补偿的效果好.

动力学模型是预测制导的基础.航天动力学的特点是模型结构已知，但实际对象的气动参数、参考面积、质量以及大气环境参数等相对动力学模型标称状态存在不确定性，理论分析和实际仿真均表明：上述不确定性会显著影响预测制导的精度.

以旋成体航天器再入动力学为例，研究发现：所有模型参数，包括大气密度、阻力系数、升力系数、参考面积、质量(ρ、CD、CL、Sref、m)等，都以乘除方式集中于气动阻力加速度和气动升力加速度的表达式中，

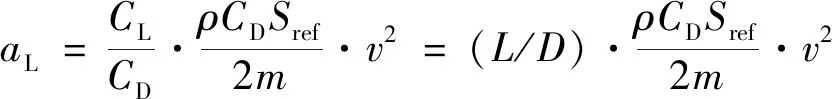
(1)

令

(2)

称之为气动综合因子，则

aD=B+·v2，aL=(L/D)·B+·v2

(3)

由于v来自导航计算，则所有模型参数的不确定性都反映在升阻比(L/D)和气动综合因子B+上.

利用导航结果和加速度计实时测量，推导求得aD、aL，进而求得(L/D)和B+，取当前状态下标称的(L/D)0和(CD)0,将大气密度、参考面积、质量等取当前状态下的标称值，解算得到当前运动状态下的标称(B+)0.

令

(4)

由于姿态运动的耦合因素，两个比值受姿态运动的扰动，需通过低通滤波得到估计值，上述过程安排在短周期的导航系统中处理.最后得到

(L/D)=KL/D·(L/D)0

(B+)=KB+·(B+)0

(5)

取来自导航计算模块的升阻比系数KL/D和气动参数综合因子系数KB+,取总控制量函数u(t)，横向“漏斗”控制律等，递推进行预测模型解算，得到终点位置和预测误差.

在预测模型中应用估计得到的(L/D)和(B+),可以显著提高轨迹预测的精度.我们称这种全数值预测方法为自适应全数值轨迹预测方法.

对面对称大升阻比飞行器，估计的参数除了(L/D)和(B+)外，还有一个横向力系数CZ，其原理和处理步骤与旋成体的情况完全相同.

1.2 标称时变动态控制增益变换方法

预测制导的核心问题是根据预测误差求解制导修正量.这个问题成为难题，是因为预测误差和制导修正量之间的关系不清楚，直至目前，尚未找到描述二者之间关系的数学模型.

以往的预测制导，普遍采用NEWTON-RAPHSO或Gauss-Newton等迭代算法；因为未知的变化巨大的非线性时变动态增益使得迭代次数多、计算量大导致预测校正周期长，影响预测制导的精度；更甚者是该方法用于再入预测制导存在迭代不收敛的问题，这也是以往再入预测制导一直没有得到工程应用原因之一.

本节以再入控制为例，从预测制导的核心问题入手，发现了影响核心问题求解的内在机理，发明了一种时变动态控制增益变换方法，为预测制导核心问题的解决创造了良好的条件.

与标称轨迹制导给出本步至下一步的制导周期内控制增量不同，预测制导给出的是从当前时刻tk至终点时刻tf的全局控制增量，可以表示成一个方波函数uk·F(tk)，F(tk)=1(tk)-1(tf).根据预测误差yk求控制增量uk,是预测制导的核心.

全局控制增量uk·F(tk)的作用，是为了消除预测误差yk+1.为了从yk求uk,需要分析u·F(t)是如何影响终点航程与目标航程之差y(t).

作为升阻比L/D和气动综合因子B+存在不确定性的非线性动力学方程，u·F(t)的影响，除了与自身u相关外，与上一时刻总控制量u1,k-1·F(tk-1)以及过程中的L/D、B+等都有关系.

定义1.1：预测误差：根据模型计算出的目标量与标称目标量之差.

定义1.2：制导校正量：本次制导控制量与前一次制导控制量之差.

定义1.3：动态增益：预测误差与制导校正量之比.

构造标称状态下的预测制导的时变动态增益：针对标称剖面、标称运动状态和标称参数，以当前时刻为自变量，用数值仿真方法构造从当前时刻到终端状态的预测制导的时变动态增益函数；当前时刻的定义域为从起始时刻到标称终点时刻，则得到从起始时刻到终点时刻的预测制导的时变动态增益函数.见图1和图2.

从物理概念的推断以及数学仿真的结果，均存在如下关系：

固定u，t越小，u·F(t)作用区间越大，|y(t)|越大，D(t)=|y(t)|/u越大；

固定u，t越大，u·F(t)作用区间越小，|y(t)|越小，D(t)=|y(t)|/u越小.

从图1看出，单位控制增量到终点误差的时变动态增益D(t)，随再入时刻的变化范围非常之大，约1800000到0.图2的物理意义可解释为：同样的预测误差，对应再入前期，所需要的校正量很小；对应再入后期，所需要的校正量巨大；受升力分量控制能力约束，过大的校正量不能实现.

将控制增量和预测误差的关系，看成一个时变动态系统的输入与输出.将图1时变动态增益函数的倒数分解为输入变换和输出变换，作用于控制增量和预测误差之间的时变动态系统，见图3，其中时变输入变换f1(t)、时变输出变换f2(t)，f1(t)f2(t)=1/D(t).D(t)为图1～2正增量增益与负增量增益的几何平均值，且限定D(t)≥1.则变换后的控制增量和预测误差之间的时变动态系统，在前述标称轨迹情形下的动态增益为1.实际再入过程中，飞行轨迹、控制指令都是非标称的，动力学参数、环境参数也相对标称值变化，上述基于标称轨迹的变换，仍具有重要效果，它使得变换后的系统，时变动态增益的变化范围大幅减小，为所有预测制导方法的实现均创造了良好的条件，更为后续采用自适应控制方法这一全新途径解决高精度预测制导问题奠定了基础.

本节的研究思路和方法见图1～3.

图1 标称轨迹制导剖面上的控制增量方波函数Fig.1 Control increment square wave function on nominal trajectory guidance profile

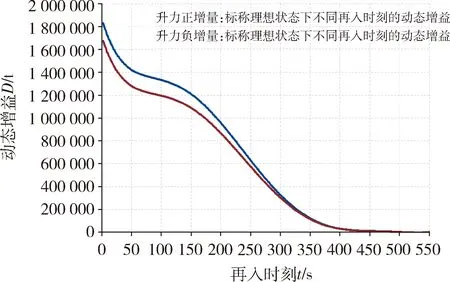
图2 基于标称轨迹的时变动态增益函数Fig.2 Time-varying dynamic gain function based on nominal trajectory

图3 基于输入输出变换的积分型控制器Fig.3 Controller with integrator based on input-output transform

1.3 一阶特征模型的自适应控制方法

在上述时变动态增益输入输出变换基础上，u和y的动态关系，相对u1和y1的动态关系，时变动态增益变化的范围大幅度降低，例如上例，从1800000～1变化到百倍左右.在500 s的再入时间内适应百倍左右的动态增益变化，仍是制导设计中必须考虑的.对输入u输出y关系建立特征模型，实时估计特征模型参数并实施自适应控制，可以进一步解决制导精度和参数鲁棒性问题.基于特征模型自适应制导律，每个预测制导周期，仅进行一次自适应制导计算，由自适应控制系统的稳定性保证预测制导的收敛性.

对不能用数学模型描述的被控对象，以往特征模型自适应控制理论，二阶特征模型被认为是最低的，其理论研究充分并有实际应用.对预测制导，首先采用二阶特征模型自适应控制，数学仿真结果表明其精度高于作为对比的无自适应能力的PID控制，效果是显著的；2014年，为了进一步提高制导精度，作者对月球-地球轨道跳跃式再入返回的自适应预测制导律进行参数优化研究.在经多轮参数尝试但效果不明显的情况下，以及一定存在更好制导结果的信念驱使下，作者将变换后的预测制导输入-输出之间的二阶特征模型改为一阶特征模型，设计了对应的制导律.通过多种子多次10240组蒙特卡洛仿真，相对二阶特征模型，基于一阶特征模型的制导律最大误差包络减小了20～30%，综合控制精度显著提高，结合上述分析和控制参数的特点，表明用一阶特征模型更适合预测制导输入输出的描述.将基于一阶特征模型的制导律回归用于文献[1]中的返回地球的直接式再入，相对二阶特征模型，同样提高了制导精度.由于二阶特征模型的参数范围和一阶特征模型的参数范围并不存在包含关系，二阶特征模型及其闭环控制的性能不能靠参数估计退化为一阶特征模型及其闭环控制的性能，也就是说，对自适应进入/再入制导这一实际工程问题，靠参数估计和参数优化，基于二阶特征模型的制导精度是无法达到基于一阶特征模型的制导精度.一阶特征模型及其控制律，具有设计工作量小，参数范围容易确定，参数调试工作量小，以及参数估计快的特点；可直接根据对象的稳定性确定参数的范围.

自适应预测制导方法见图4，由于是增量控制，故包含积分器.基本公式见(14)～(22).

一阶变系数模型：

y(k+1)=α(k)y(k)+β0(k)u(k)

(6)

定义回归向量

φT(k)=[y(k-1),u(k-1)]T

(7)

定义参数向量

θT(k)=[α(k),β0(k)]T

(8)

图4 自适应预测制导方法示意图Fig.4 Schematic diagram of adaptive predictive guidance method

参数估计公式为

θ(k)=θ(k)+

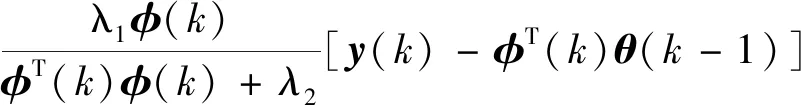
(9)

其中λ1,λ2是正的常数.

θ(k)=Fθθ(k)+(1-Fθ)θ(k-1)

(10)

其中，Fθ为对参数向量θ(k)的一阶滤波的系数，0≤Fθ≤1，通过Fθ在[0，1]区间的数学仿真寻优确定.

参数限制

a(k)∈[0.1, 0.99]

(11)

β0(k)∈[0.003, 1.00]

(12)

线性反馈控制

u(k)=-L1α1(k)y(k)/(β0(k)+λ)

(13)

L1是小于1的正数，λ>0，均为控制律设计参数.

由于倾侧角的上、下界限制，故对u(k)也加如下限制，

u(k)∈

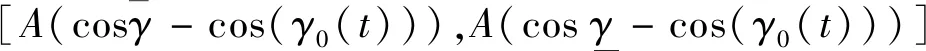
(14)

因一阶模型不存在二阶模型两个参数之和的约束，参数范围确定简单.

对预测制导一阶特征模型的机理分析： 预测制导误差的求取：当前状态积分到终点，求得航程，减标称航程(常数)，得到预测误差；与通常控制周期内的状态变化不同，预测制导中的预测误差是一个较长时间区间(当前时刻至终点状态时刻)的积分过程，动态过程都融入较长时间的积分中，因此用单调的一阶特征模型更适合.进一步分析：由于预测模型是积分有界的、可解的，以及输出相对输入是单调的，因此它是开环稳定的最小相位系统；预测误差的求解过程：首先是再入动力学方程求解，这是一个三维动态矢量二阶非线性微分方程从当前时刻至终点时刻的积分，得到航程，再减去标称航程，得到航程预测误差.由预测误差的求解过程可知，预测误差相对再入时间，是一阶非线性微分方程形式，所以再入预测制导的控制模型用一阶特征模型是准确的.当然二阶特征模型也可以使用.由于二阶特征模型对应修正量的二维搜索，一阶特征模型对应修正量的一维搜索，而再入预测制导求解本身就是修正量的一维搜索，二维搜索在速度或效率上明显不如一维搜索，所以用一阶特征模型，有限时间内取得的精度更高.

自适应预测制导，是两级校正：一级校正是标称时变动态增益变换，任务前根据标称轨迹设计，是“已知的变化”；二级校正是标称之外的不确定性，任务中实时在线校正，是“真正的变化”.

有关一阶特征模型的自适应控制方法的收敛性，见文献[13]和[16].

1.4 自适应预测双环制导方法

1.1～1.3节给出了包含自适应轨迹预测、时变动态控制增益变换和基于一阶特征模型自适应控制的自适应预测制导方法.相对标称轨迹制导方法，自适应预测制导方法的计算量仍是较大的，这使得制导控制周期仍较长.在两次预测制导控制间隔内，制导系统开环，受动力学参数不确定性和导航误差影响，实际轨迹不能准确跟踪预测制导轨迹，导致最终制导误差.为解决该问题，在预测制导周期内，引入短周期的标称轨迹自适应纵向和横向制导律，形成以自适应预测制导为外环、标称轨迹自适应纵向和横向制导为内环的高精度、强鲁棒的自适应预测双环再入制导方法.在外环给出一级制导指令和轨迹预测的基础上，内环通过实际轨迹与预测轨迹的偏差，给出纠正轨迹偏差的二级制导指令，解决预测制导周期内实际轨迹对预测轨迹的强跟踪问题，由于内环含有过载直接测量量，内环还具有减小导航误差对最终制导精度影响的作用.自适应预测双环制导控制方法示意图见图5.

另一方面，在已有标称轨迹自适应制导基础上，由于再入初始条件、气动、动力学与环境参数与标称值的不一致，导致实际飞行轨迹远离标称轨迹，标称轨迹制导律存在内在固有问题.而如果有从当前点至目标的可行轨迹，则制导指标很容易实现.为了实现高精度制导，也需要在标称轨迹自适应制导之外，有根据误差不断调整的从当前点至目标的可行轨迹.

综合上述两方面，双环制导是高精度制导所要求的，无论从预测制导出发，还是从标称轨迹制导出发，殊途同归的结果.

从图5看出，外环的自适应预测制导以导航系统给出的运动状态作为初值，以动力学与环境的综合参数估计补偿动力学预测模型的不确定性，实时规划出可行轨迹和制导剖面，内环实时跟踪外环规划的轨迹，并根据跟踪误差，修正制导剖面以减小跟踪误差，上述过程按照外环长周期、内环短周期的方式持续进行直到达到终端条件.因此，双环制导是预测制导与标称轨迹制导的深度融合.

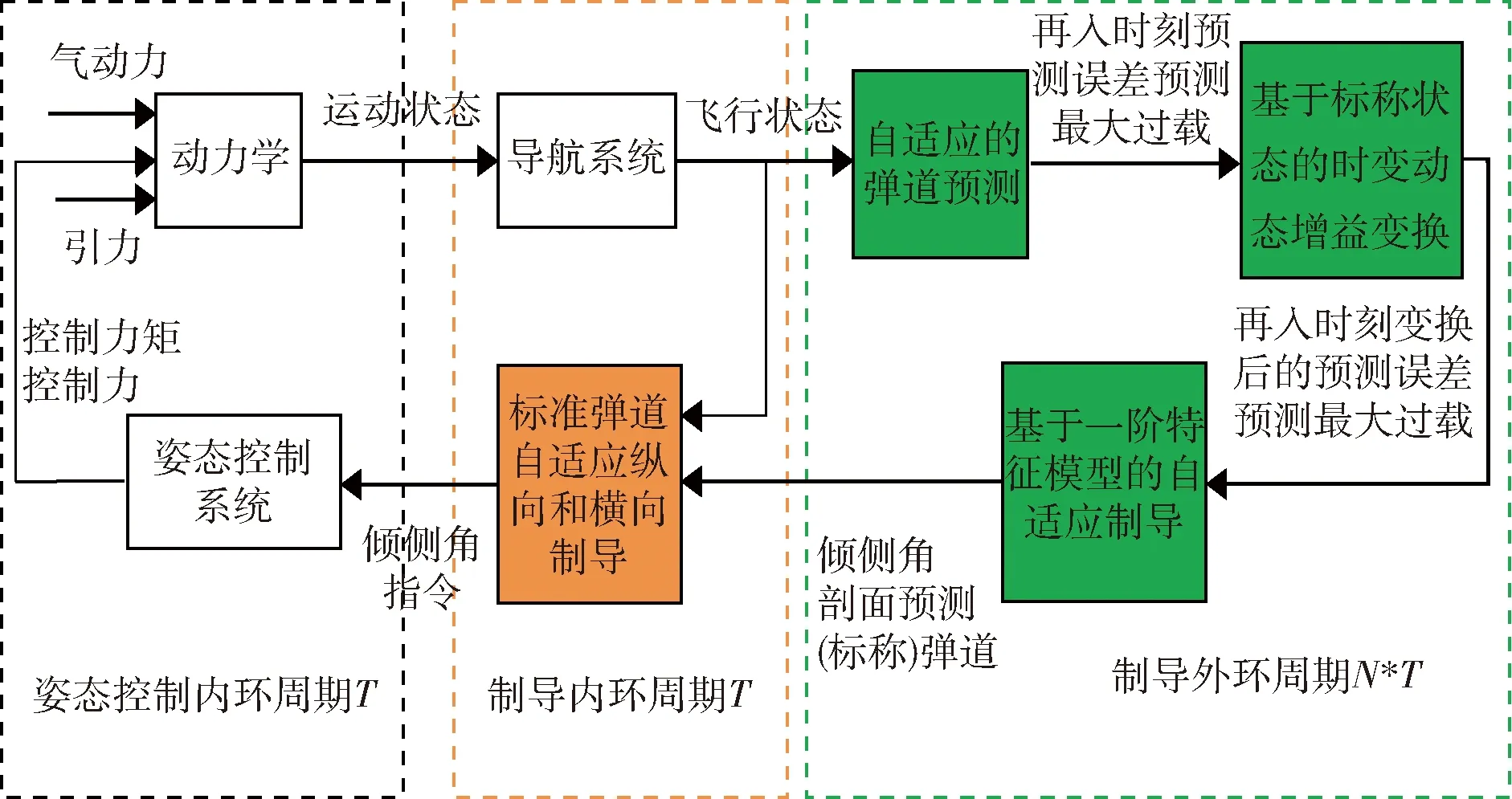
图5 自适应预测双环制导示意图Fig.5 Schematic diagram of adaptive predictive double loop guidance

双环制导是在控制计算机性能较差导致预测制导的周期校长，为实现高精度制导而采用的.

1.5 内环标称轨迹自适应制导方法

将标称轨迹的状态变量存储在船载计算机中，与导航系统计算出的飞船对应的状态量相比较，得到误差信号，利用误差信号形成制导规律.标称轨迹制导方法，要求存储的状态变量为给定自变量的函数，有选时间作自变量的，也有选速度或航程作自变量的.这里选依时间为自变量的制导方法，制导律分为纵向制导律和横向制导律.

纵向制导律选择如下的形式:

(15)

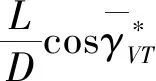
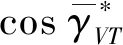
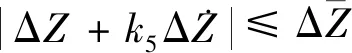
(16)

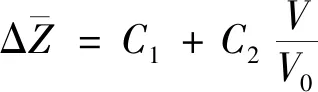
(17)

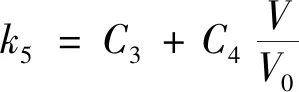
(18)

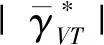
图6给出了横向制导倾侧角符号翻转边界.可以看出当飞行器横向航程碰到预先设计的边界时，倾侧角符号进行翻转，从而控制飞行器横向位移向相反的方向飞行.随着接近飞行末端，横向航程边界也越来越窄，最终使横向航程控制在较小的范围内.

图6 横向制导倾侧角符号翻转边界Fig.6 Sign flip boundary of lateral guidance bank angle

由于横向制导输出倾侧角的最终值，除了内环标称轨迹制导含横向制导外，预测模型中也包含同样的横向制导规律.

1.6 约束预判与制导处理[4,6]

再入过程的约束一般包括最大过载、最大动压、峰值热流等，终端要求也有更复杂的情况，如大升阻比飞行器末端能量管理终端要求航程、高度、动压、弹道倾角等的综合约束.以最大过载的控制或防范为例，说明约束预判和制导处理的原理.

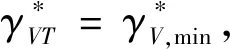
约束预判与制导处理示意图见图7.

更复杂的约束要求，需根据实际情况处理[15].

1.7 实时制导前的在线轨迹规划

上述1.1～1.6节都是自适应预测制导用于实时制导的方法.当然，自适应预测制导也可作为实时制导之外的在线轨迹规划.典型场景特征是：距实时制导开始时刻还有充足时间，但运动状态已偏离标称轨迹.如果仍以预装标称轨迹和制导剖面作为后续实时自适应预测制导的初值和初始制导剖面，会造成自适应预测制导的初值和初始制导剖面误差过大，影响制导系统的过渡过程，对约束的处理也有影响.将自适应预测制导用于实时制导前的在线轨迹规划，即：以实际运动状态为初值，动力学与环境综合参数取标称值，按照标称时变动态控制增益和一阶特征模型自适应控制方法，在线迭代规划出后续制导所需的可行轨迹和制导剖面，作为后续实时自适应预测制导的初值和初始制导策略，不失为解决问题的好办法.解决问题的思想同作者的文章[17]一致，只是制导律从PI改为增量式一阶特征模型自适应控制.

图7 过载保护逻辑示意图Fig.7 Logic schematic diagram of overload protection

2 应用、推广与应用研究

2.1 嫦娥五号飞行试验器月地返回跳跃式再入[8]

2014年10月24日至11月1日，嫦娥五号飞行试验器完成了月地返回轨道跳跃式再入飞行实验.整个任务剖面和返回再入飞行任务剖面如图8～9所示.

嫦娥五号飞行试验器的返回再入制导导航与控制，采用高精度星敏感器(ST)/卫星导航接收机(GNSS)/光学惯性测量单元(IMU)组合导航系统，导航初值以及第一次再入大气层之前、第一次跃出大气层之后到第二次再入大气层之前的位置、速度测量值均来自GNSS接收机，姿态四元素初值来自在轨高精度的ST/IMU组合姿态确定系统，在巡航段设置精确标定IMU常值偏差、刻度因子偏差与安装偏差等，嫦娥五号导航系统是高精度的导航系统，与美国阿波罗、猎户座高精度导航系统相当.

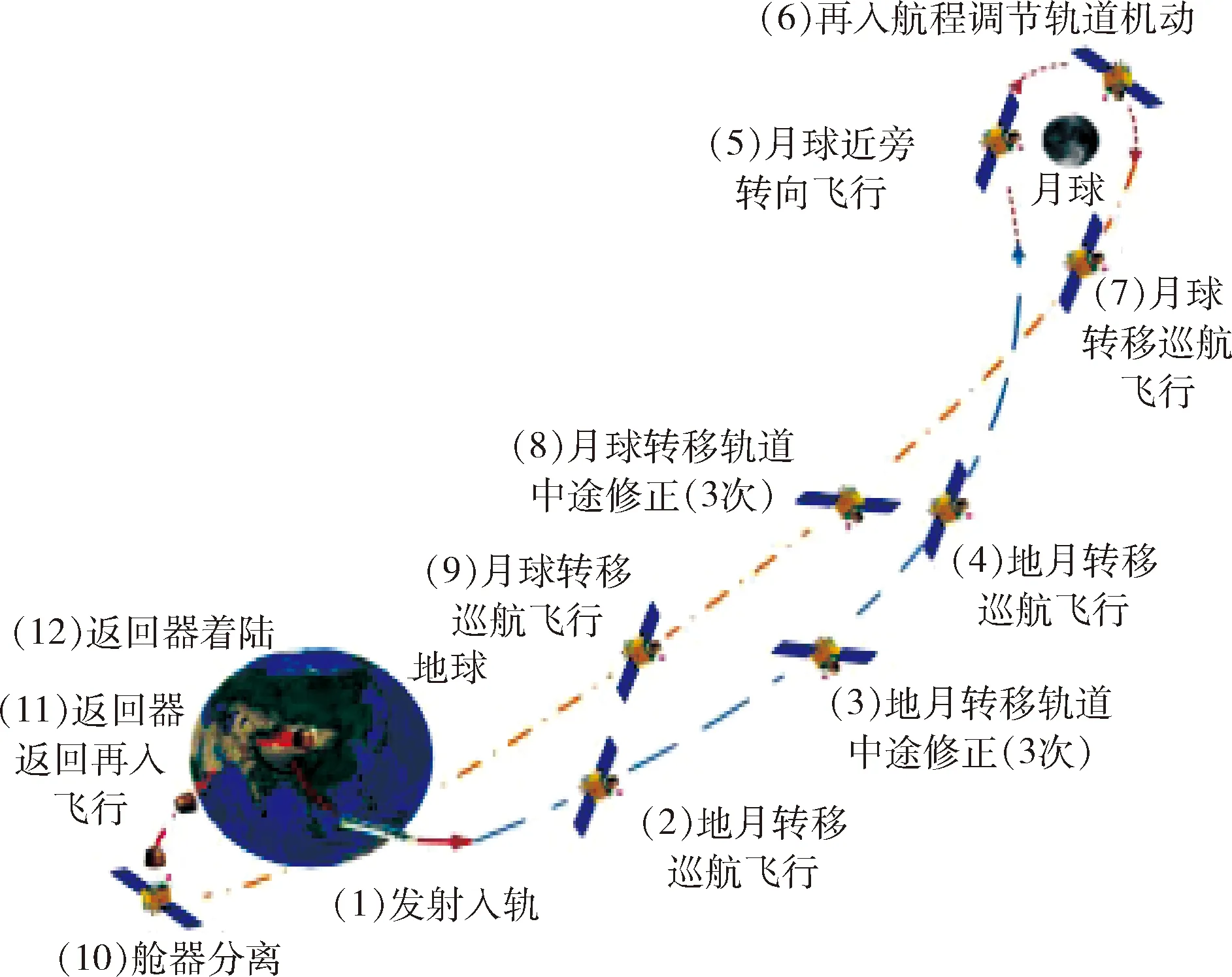
图8 飞行试验任务剖面Fig.8 Mission profile of flight test

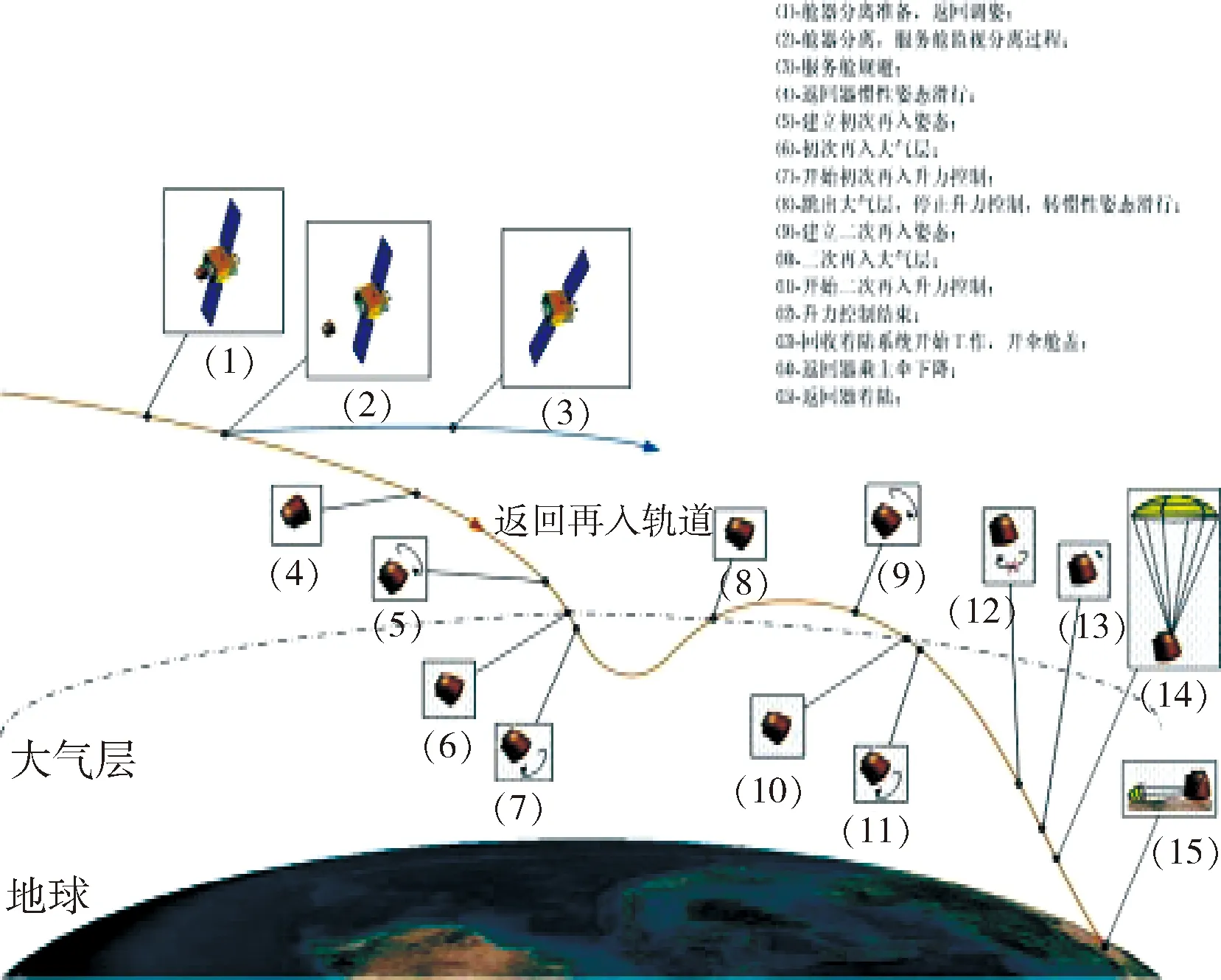
图9 返回再入飞行任务剖面图Fig.9 Return and reentry mission profile

返回试验器进入大气层后，经历了初次再入、自由飞行、二次再入阶段，从进入大气到开伞总航程6 654 km，返回过程中纬度变化范围大，大气密度摄动大，由于再入过程的烧蚀不可能按照设计的理想状态，气动参数相对标称状态存在不确定性，制导导航和控制系统的设计能否对这些摄动因素具有足够的自适应能力，是本次任务成败的关键.

返回试验器制导导航和控制系系统应用了自适应轨迹预测、时变动态控制增益变换、基于一阶特征模型自适应控制、自适应预测双环制导方法以及基于升阻比在线实时估计的标称轨迹自适应制导律.

本次跳跃式再入的第一次再入最低点：62.862 km，跃出段最高点：104.322 km.第一次再入最大轴向过载：4.72(指标：<7)，第二次再入最大轴向过载：4.06(指标：<7)，见图10～11.10 km开伞点：纵向误差：0.248m(指标:<30 km)，横向误差：0.445 km(指标:<20 km)，总误差：0.509 km，开伞点精度是目前国际上航天器月地返回的最高精度.应用自适应预测制导的开伞点精度相对以往载人飞船标称轨迹制导方法有数量级的提升.

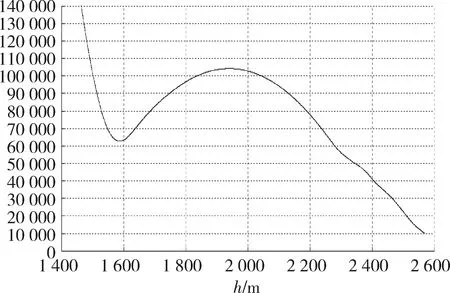
图10 嫦娥五号飞行试验器再入高度-时间曲线Fig.10 CE-5 Flight tester reentry height-time curve

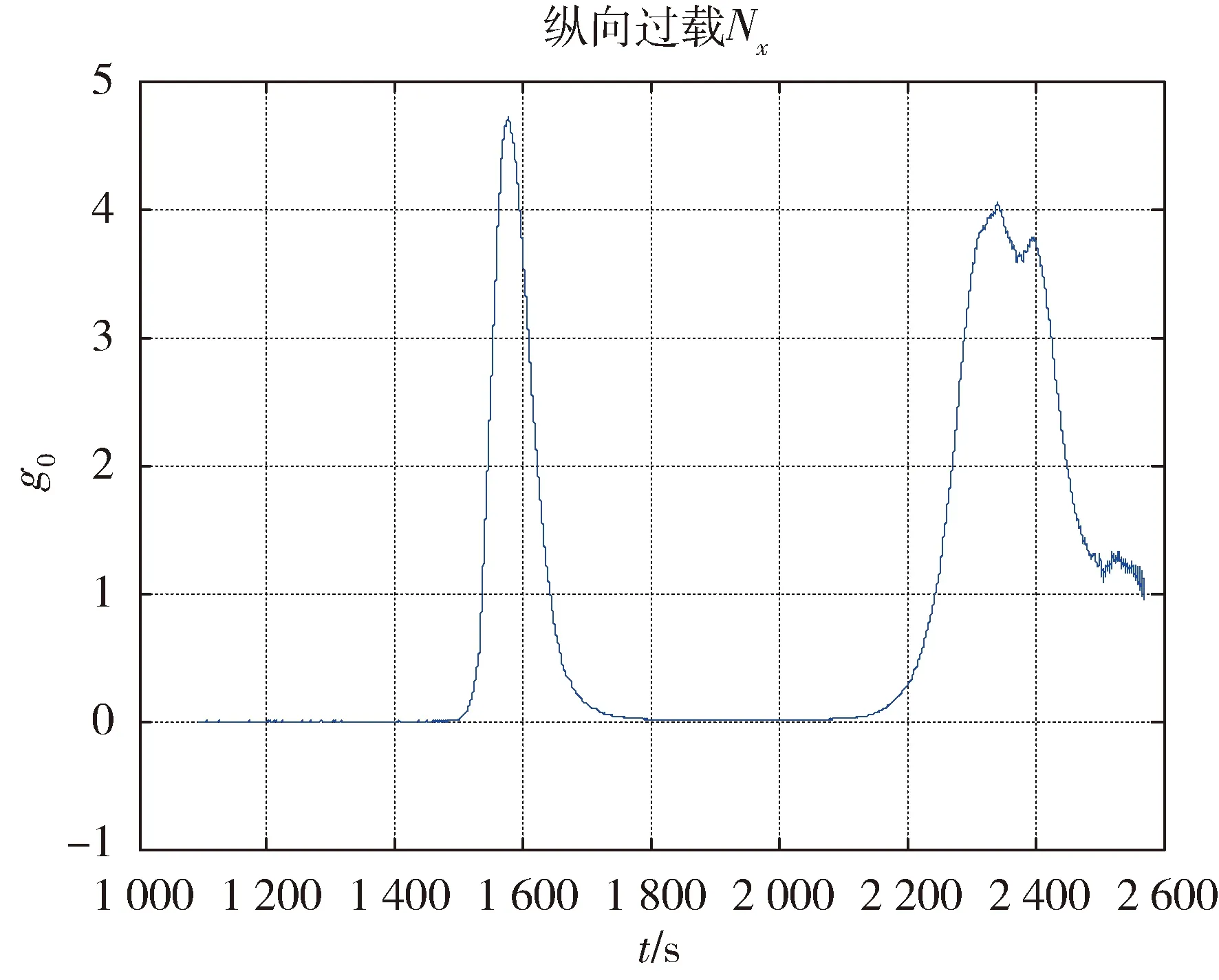
图11 嫦娥五号飞行试验器再入过载-时间曲线Fig.11 CE-5 Flight tester reentry overload-time curve

2.2 推广

自适应预测制导方法已成功应用于嫦娥五号飞行试验器[8]，将继续用于嫦娥五号及后续月球探测器，并推广应用于我国载人航天器以第一、第二宇宙速度的直接式和跳跃式再入设计[9-11]，待飞行最终验证.

2.3 应用研究

除上述成功应用和推广应用外，还完成了一些以典型任务为背景的应用研究，包括：地球轨道直接再入[1,9-10]、火星进入[12,15]与火星大气捕获[13]、大升力体初始再入[14]、末端能量管理[15]、进场水平着陆[16]等.其中，(1)地球轨道直接再入、火星进入、大升力体初始再入与月球-地球轨道第二宇宙速度的跳跃式再入在动力学方程形式和目标特性上是一致的，只是气动参数、环境参数有差别，在再入走廊和标称弹道设计基础上，对火星再入和大升力体初始再入，在应用本方法并进行制导参数优化设计的过程中，需要将开伞或末端能量管理的包括多飞行参数综合的交班条件作为约束来考虑[12,14-15]；(2)火星大气捕获，与再入问题类似，本质上也是利用调节气动升力的可控范围，精准控制选定的目标量.但不论怎样选择目标量，都是以实现捕获指标且气动捕获前后所需速度增量最小来衡量.文献[13]分别选定远拱点半径、平面内改变远拱点高度所需速度增量为预测校正目标，设计自适应预测制导算法.数学仿真结果表明，后一种目标的选择，自适应预测制导的精度、收敛性都更好；(3)对大升力体末端能量管理段，由于控制量包括倾侧角、攻角以及终端多约束条件，包括航程、高度、速度、速度倾角等参数的综合指标作为被控目标，根据控制系统对控制量与被控制量具有单调关系的要求，分阶段定义控制量与被控制量，分别建立动态增益关系与对应的自适应控制，实现大升力体末端能量管理的制导要求[15]；(4)大升力体可重复使用飞行器(RLV)自动着陆，将着陆段分为初始滑翔段和最终指数拉平段，利用平衡滑翔条件和关于高度的指数函数来参数化两个飞行子阶段的制导指令，重点考虑终端约束和过程约束，根据自适应预测制导方法，设计预测校正规律，证明了制导方法的稳定性以及有限步收敛的性质，给出了参数选取的规则[15-16].

从航天器运动学和动力学具有统一形式以及自适应预测制导的特征，自适应预测制导方法无疑也适合发射段制导、载人飞船应急救生以及无大气或稀薄大气环境的轨道控制相关的制导过程，对这几方面，正在开展了面向飞行任务的应用研究工作.

综上所述，自适应预测制导方法可以作为航天器的一种统一的制导方法，是一种提炼智能特征的自主制导方法.

3 展 望

在离线或实时制导前的在线轨迹规划基础上，应用自适应预测制导方法，在较大初始条件、参数误差条件和控制约束下，可以满足终端约束和过程状态一般性约束.

未来需要研究的是可达域内满足综合型终端约束和过程状态复杂约束的最优或可行轨迹的离线或在线实时规划问题.

无论制导还是控制问题，即给定终端状态要求(约束)，在满足动力学方程前提下，以及初始状态范围和过程运动约束、控制约束下，求解控制和状态轨迹，都可转化为约束条件下的最优控制问题，应用一般性的数值直接求解方法，问题都转化为非线性规划问题求解.这尤以带约束的伪谱法轨迹优化以及带约束的凸优化在当前学术界最为盛行，二者都是直接数值优化方法.非线性规划方法存在的主要问题是：(1)解的存在性：主要牵涉终端约束、过程状态约束与初值、控制约束、动力学方程是否自洽？作为主要的性能要求，终端约束、过程状态约束通常需要反复迭代计算、折衷方能确认，否则一旦优化不出结果，无法确认是求解器问题还是性能要求提法不合适；而反复迭代计算后确认的性能要求(终端约束、过程状态约束)，则至少意味着标称状态下优化问题有解，给后续实时制导提供了余地；(2)最优解与鲁棒性的矛盾：为了能在动力学与环境参数不确定条件下闭环制导或控制系统仍稳定并保证指标要求，给出的解必须对参数不确定性具有鲁棒性，而最优解通常用尽制导或控制余量以追求最优性，从而失去了应对不确定性的鲁棒性.该问题可通过牺牲一部份最优性、保留控制余量的约束以及估计模型重要参数的方法给予部分解决；(3)解的精度问题：精度问题与分时阶段划分与各分时阶段离散点的选取有关，具体精度则靠事后验算；(4)求解器问题：当形成数值直接法求解受限最优控制问题后，求解器成为关键性问题.目前国内优化方面的研究，仿真和设计都在是用国外的开源求解器，不能满足在轨使用的要求，国内必须研发具有自主知识产权的求解器.

非线性规划作为离线设计标称轨迹是可行的，因为可以在地面，进行反复迭代尝试.如果进行一次性在线标称轨迹设计，即使是在轨实时制导前的非实时场合，对非线性规划求解器的可靠性、灵活性、天地交互性、快速性的要求非常高，是一个亟需解决的问题.将离线或一次性在线设计的标称轨迹提供自适应预测制导作为初值使用，可解决过程状态复杂约束的高精度制导问题.

设想若能按照满足精度要求的制导周期持续进行在线轨迹规划，则传统意义上的制导算法降级为在线轨迹规划的内环，作用局限于小范围内的更高精度；如果在线轨迹规划与控制系统联合的精度满足要求，即用在线轨迹规划的输出直接作为控制系统的输入，则原则上可以取消制导算法.除了计算速度是重要的制约因素外，可解性、鲁棒性、精度的收敛性与收敛速度仍是制约周期性在线轨迹规划的理论与实用制约因素.此路是否可行，是一个尚未解决的问题.

致谢：

为纪念杨嘉墀先生诞辰100周年，以及先生提出将航天智能自主控制确定为未来航天控制发展方向，撰写此文.感谢与作者共同从事自适应预测制导与应用的吴宏鑫、杨鸣、董文强、张钊以及拓展应用研究的李毛毛、唐青原、王晓磊等.