基于特征建模的空间非合作目标姿态智能测量方法*
王 立,顾营迎
0 引 言
空间非合作目标姿态测量,是空间在轨服务的关键技术,可以为空间目标的抵近、绕飞、捕获提供必要的导航信息[1],可以进一步扩展空间目标的操作能力[2],是当前研究的热点和难点问题.
利用激光测量体制,进行非合作目标姿态的测量,具有抗杂光能力强、阳照/地影区全天时工作、目标尺度、距离信息丰富等特点,是当前研究较多的一种非合作目标测量体制[3-4].其基本原理是,利用激光的测角和测距技术,获得能够表征目标空间位置和姿态的点云数据,通过点云数据处理技术,解算出目标相对于测量敏感器的位置和姿态.常用的点云姿态测量方法大多基于点云的匹配技术:文献[5]提出的ICP方法奠定了点云姿态精确匹配的基础,但是该方法存在对目标的初始姿态敏感,容易陷入局部最优的问题,同时存在计算方法的时间复杂度的高,解算姿态的实时性差的问题[6].为了改善ICP方法的初始姿态敏感问题,有文献在进行ICP之前加入了点云粗匹配环节,先后提出不同的点云粗匹配方法[7],如基于主成份分析的方法、基于哈希索引表的方法和基于局部几何特征的方法等等[8-10].为了改善ICP算法的时间复杂高问题,相关文献提出了基于最近邻的快速查找方法和模型点云的K-D树构建法等等[11-12].随着近年来人工智能技术的发展,也有学者尝试用深度学习的方法解决非合作目标姿态测量问题[13-14],但存在的问题是学习的网络规模庞大、复杂,真实在轨环境下可供学习的样本数据少,难以实现在轨实时应用.
为解决以上非合作目标位姿测量面临的在轨工程化应用问题,本文引入控制理论中的特征建模思想[15],面向目标姿态参量,寻求目标点云数据的简化表征方法,进而建立适用于空间实时应用的神经网络模型,实现了一种基于点云特征建模的空间非合作目标姿态智能测量方法.为空间非合作目标姿态的在轨实时测量应用,提供了一种可行的智能化方案.
1 目标点云的特征建模
1.1 特征建模思想
随着被控对象的结构越来越复杂,对目标精确动力学建模越来越困难;另一方面,工程应用上,控制器设计在满足性能指标要求下越简单越好.为了解决这一问题,文献[16]提出了特征建模的思想和理论方法,主要用来解决对于高阶复杂对象,在满足工程控制性能要求下,如何设计一个低阶控制器来对系统实施控制,从而化繁为简解决工程应用中复杂对象的控制问题.
在控制领域中,特征建模的主要特点有[16]:
1)在同样输入控制作用下,对象特征模型和实际对象在输出上是等价的,在稳定情况下,输出是相等的.
2)特征模型的形式和阶次除考虑对象特征外,主要取决于控制性能要求.
3)特征模型建立的形式应比原对象的动力学方程简单,易于控制器设计,工程实现容易方便.
4)特征模型与高阶系统的降阶模型不同,它是把高阶模型有关信息都压缩到几个特征参量中,并不丢失信息.
总体来说,特征建模的核心思想就是,面向工程应用,化繁为简,抓问题的主要矛盾和目标对象的本质特征,来有效解决问题.
当前,在非合作目标激光测量领域,也遇到了特征建模提出初期的类似的问题:一方面,为了精确表征目标的形态,期望空间目标的激光点云数据越多越好;另一方面,在空间计算资源极度受限的情况下,大多点云姿态处理算法的计算复杂度又非常的高.这一突出矛盾,使得大多数非合作目标姿态测量算法,很难实现保精度条件下的在轨工程应用.
为此,本文将特征建模思想从控制领域,引入非合作目标激光测量领域,以获得非合作目标的姿态为目的,从点云数据中寻找能代表目标姿态的主要特征,实现目标点云数据量的压缩,进而实现目标姿态高效、高精度的测量和估计.
1.2 目标姿态的点云特征参量构建
对于用激光雷达获取的目标点云来说,其最基本的信息,由测量敏感器空间直角坐标系下的一组XYZ坐标值组成.将这组点云坐标值中表示X轴方向的坐标值用列向量A来表示,表示Y轴方向的坐标值用列向量B来表示,表示Z轴方向的坐标值用列向量C来表示,则目标点云的协方差矩阵M定义为:
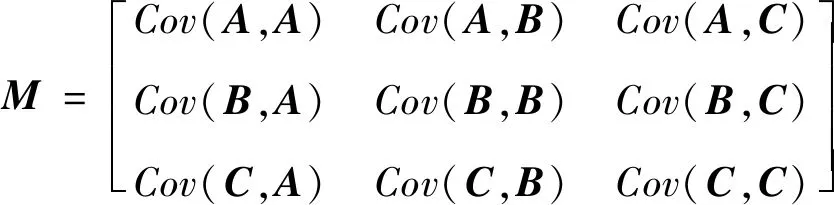
(1)
根据协方差矩阵的性质可知,目标点云的协方差矩阵为对称矩阵,即Cov(B,A)=Cov(A,B),Cov(C,A)=Cov(A,C),Cov(C,B)=Cov(B,C).因此目标点云的协方差矩阵M有6个有效的元素参数:Cov(A,A),Cov(B,B),Cov(C,C),Cov(B,A),Cov(C,A),Cov(C,B).对于坐标列向量A和B来说,其协方差Cov(A,B)用下述公式计算:
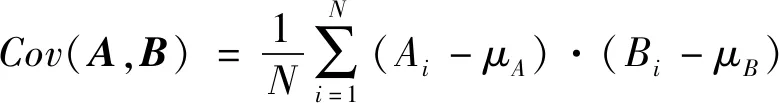
(2)
其中,Ai表示列向量A的第i个元素值,Bi表示列向量B的第i个元素值,μA是列向量A的均值,μB是列向量B的均值,其他列向量间的协方差计算方法与此类似.
通过以上定义,已知目标的一组点云就可以计算其对应的协方差矩阵M,用点云的协方差矩阵M的6个有效元素组成向量,来表征目标的点云姿态信息.
1.3 协方差矩阵特征与目标姿态的关系
根据特征建模思想,在1.2节实现了目标点云的协方差矩阵特征定义.但要实现目标姿态测量的目的,还需要定义的点云的协方差矩阵特征,能够有效表征目标的姿态.
对于刚性体非合作目标来说,从点云目标的协方差矩阵定义可知,目标的姿态与其点云的协方差矩阵有着对应的关系,可以将目标的姿态和其对应的协方差矩阵描述成如下函数关系:
Mcov=f(p,q,γ)
(3)
其中,Mcov为目标姿态p下对应的协方差矩阵,q为目标的几何形态因子,对于同一个刚体目标来说,几何形态因子q是固定的.γ在此表示影响点云协方差矩阵Mcov的其它弱相关参量,如点云的测量噪声、点云的采样数量等等,但是整体来看这些参量对点云协方差矩阵Mcov的影响非常有限,可根据特征建模思想,将这些参量作为次要矛盾考虑.因此,协方差矩阵的数值只与目标姿态p有强相关性,在几何形态因子q固定,γ作为弱相关参量予以忽略的条件下,不同的姿态p对应着不同的协方差矩阵Mcov.
如图1所示为同一目标,不同姿态下的三组点云集(红、绿、蓝).图2为图1中红色点云集的空间坐标数据,分别对应目标不同扫描点的x、y、z方向的空间位置,一组点云集中有多少个扫描点,就对应多少组这样的三维空间位置坐标值.同样的对于图1中的绿色、蓝色点云集,也分别有与其对应的空间坐标数据.为了观察目标不同姿态下点云集的数据曲线特征,分别对三组点云集的x方向、z方向的空间坐标数据进行曲线绘制,以坐标数据的序号为横轴,分别以x、z方向的空间坐标数值作为纵轴.依据上述规则绘制的曲线如图3所示.从图中可以看到,不同姿态下,目标点云集的数据坐标曲线形状是各不相同的.依据1.2节对目标点云协方差矩阵的定义,可以看到,协方差矩阵正是描述这种曲线与曲线自身、曲线与其他曲线间关系的一种有效的参数化表示方法.
通过协方差矩阵的这种统计特征参量,可以很好的综合利用目标的所有点云数据,实现目标点云特征的稳定、鲁棒抽取,为后面目标姿态的表征、测量打下基础.另一方面,可以看到点云协方差矩阵,对目标的几何形状和姿态具有表征作用,这是本文开展基于学习的姿态测量方法的关键.

图1 同一目标、三种姿态下的点云数据Fig.1 Point cloud data for three pose of the same target
图2 目标点云集的空间坐标数据Fig.2 Spatial coordinate data of target point cloud
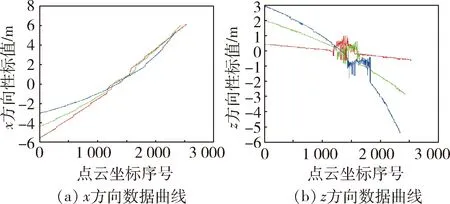
图3 目标不同姿态下点云集的空间坐标数据曲线Fig.3 Spatial coordinate data curve of point cloud in different pose of target
2 映射模型的选择与建立
2.1 智能测量的基本原理
本文提出的空间非合作目标姿态智能测量方法的基本方案如图4所示,通过前面小节的分析可知,不同姿态下的目标点云对应了不同的协方差矩阵特征,所以点云协方差矩阵与目标的姿态应该具有某种非显式的函数关系f(·),如果找到这种关系,那么就可以通过目标的协方差矩阵,估计出其对应的姿态值α、β、γ.而神经网络模型正是可以通过大量的数据学习,实现对于某些非显式的函数关系的近似逼近,从而完成点云协方差矩阵与目标姿态间对应关系的映射,进而解决基于点云的非合作目标姿态测量问题.
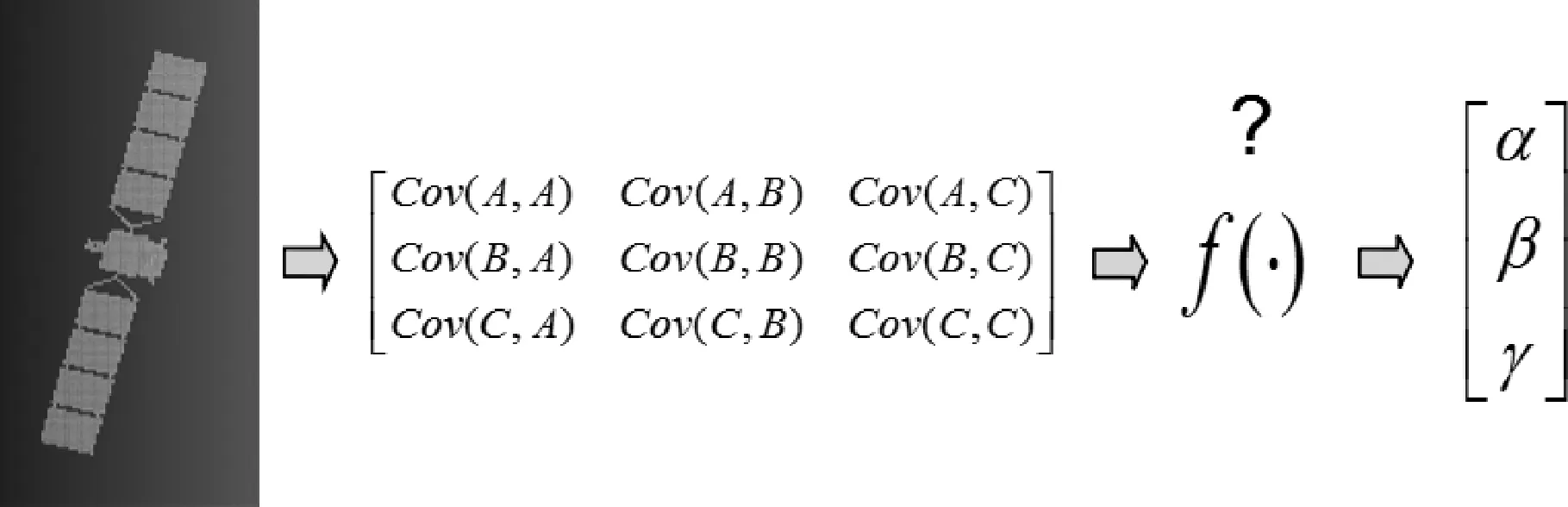
图4 非合作目标姿态智能测量方案Fig.4 Intelligent pose measurement scheme for non-cooperative target
2.2 网络训练数据集
利用神经网络进行点云协方差矩阵与目标姿态间的非显式函数关系f(·)的学习,面临的首要问题是网络训练的数据集问题.
为了获得目标点云数据和姿态标注,应用仿真的方法模拟激光位姿敏感器在不同角度对目标进行点云扫描,获得目标不同姿态的点云数据,如图5所示.考虑到在4n空间内,目标姿态数据处理量过大,也使得神经网络模型对计算机硬件和软件要求较高.因此,在不影响算法验证效果的前提下,对数据规模和解的空间进行缩减,展示本文提出的目标姿态智能测量方法的可行性.
将目标的姿态限定在绕z轴0°~180°的范围内,将其他两轴固定不变.这样本节要研究验证的问题为,通过绕z轴0°~180°的目标点云的协方差矩阵数据与其对应的角度标注,训练神经网络,学习出点云协方差矩阵与目标姿态间的对应关系模型,从而对于给定一个目标姿态的点云,模型都可以精确的预测出对应目标的姿态.图6为目标绕z轴0°~180°旋转,仿真点云不同姿态下的协方差矩阵各元素值的分布情况.从中可以看到不同的目标姿态,其协方差矩阵各元素组成的空间向量各不相同,说明通过目标协方差矩阵来估计目标的姿态是可行的.
运用仿真的方法,对目标进行不同姿态下的激光扫描,目标姿态旋转步长为1°,形成目标不同姿态的点云数据.同时对相同姿态的点云数据加入均值为零、标准差为0.008 m的高斯噪声,形成相同姿态下的50组噪声数据.最终形成9050条点云姿态数据.
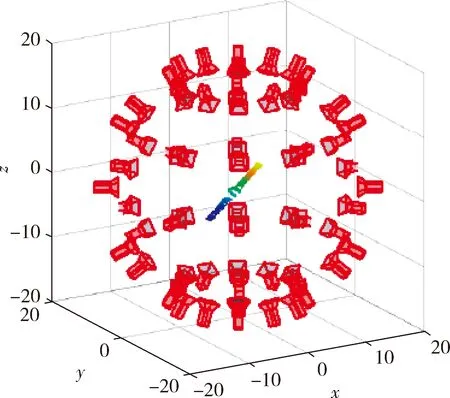
图5 目标的全方位点云数据获取Fig.5 Omnidirectional point cloud data acquisition
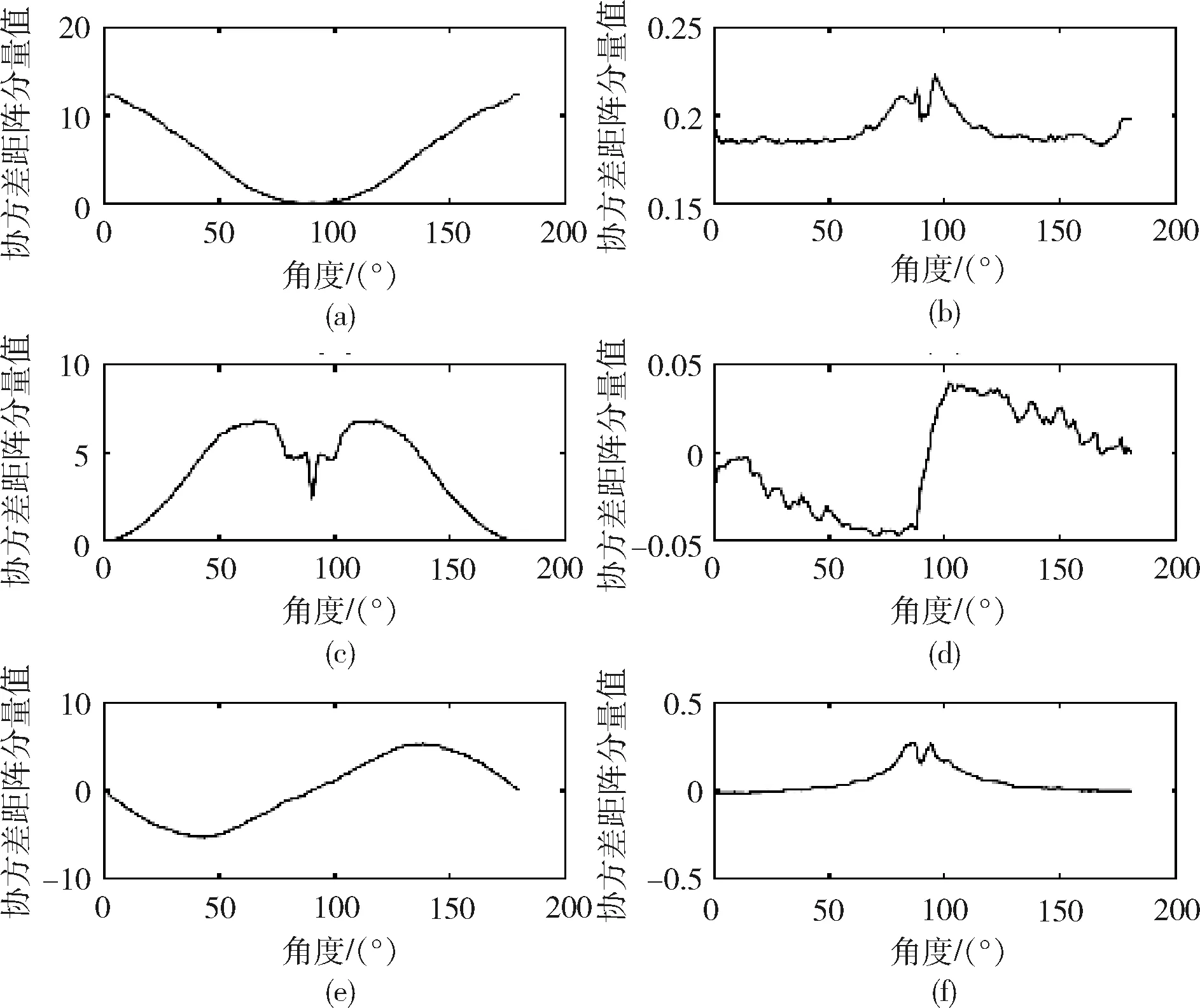
图6 目标不同角度下的点云协方差矩阵元素值Fig.6 Covariance matrix value of point cloud for different pose of target
2.3 神经网络模型的设计与训练
为了实现目标点云协方差矩阵与对应姿态间关系的学习,建立如图7所示的神经网络结构.模型由一个输入层、两个隐藏层和一个输出层组成,输入层的输入个数为6个,分别对应点云协方差矩阵的主对角元素M(1,1)、M(2,2)、M(3,3)和非主对角元素M(1,2)、M(1,3)、M(2,3).第一个隐藏层为全连接层,具有六个输出,激活函数设定为Sigmoid函数;第二个隐藏层有两个输出;输出层由一个神经单元组成.输出层的输出为目标旋转的姿态角度值.神经网络的输入x与输出y间的数学关系如式(4)~式(8)所示.网络的权重参数共计有50个,偏置参数共计有8个.
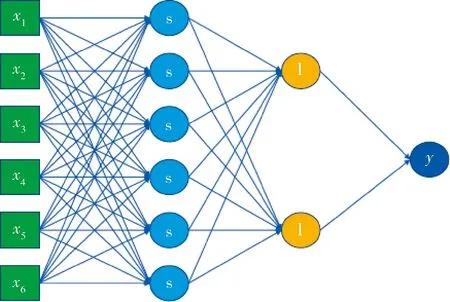
图7 神经网络结构Fig.7 Neural network structure
x=[x1x2x3x4x5x6]T
(4)
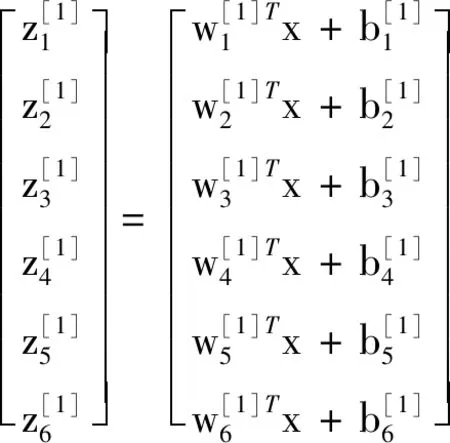
(5)
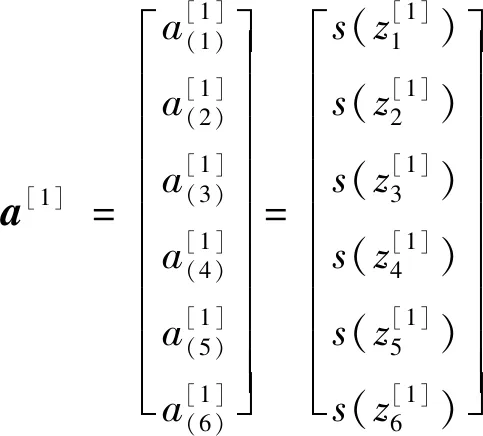
(6)
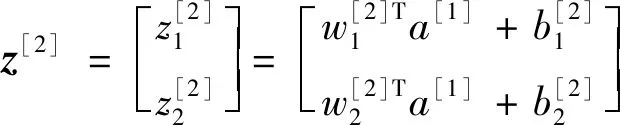
(7)
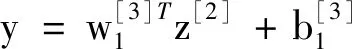
(8)

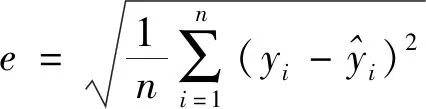
(9)
图8为最终网络训练的结果,误差损失函数已经平稳达到较小的数值,满足姿态预测精度的要求.
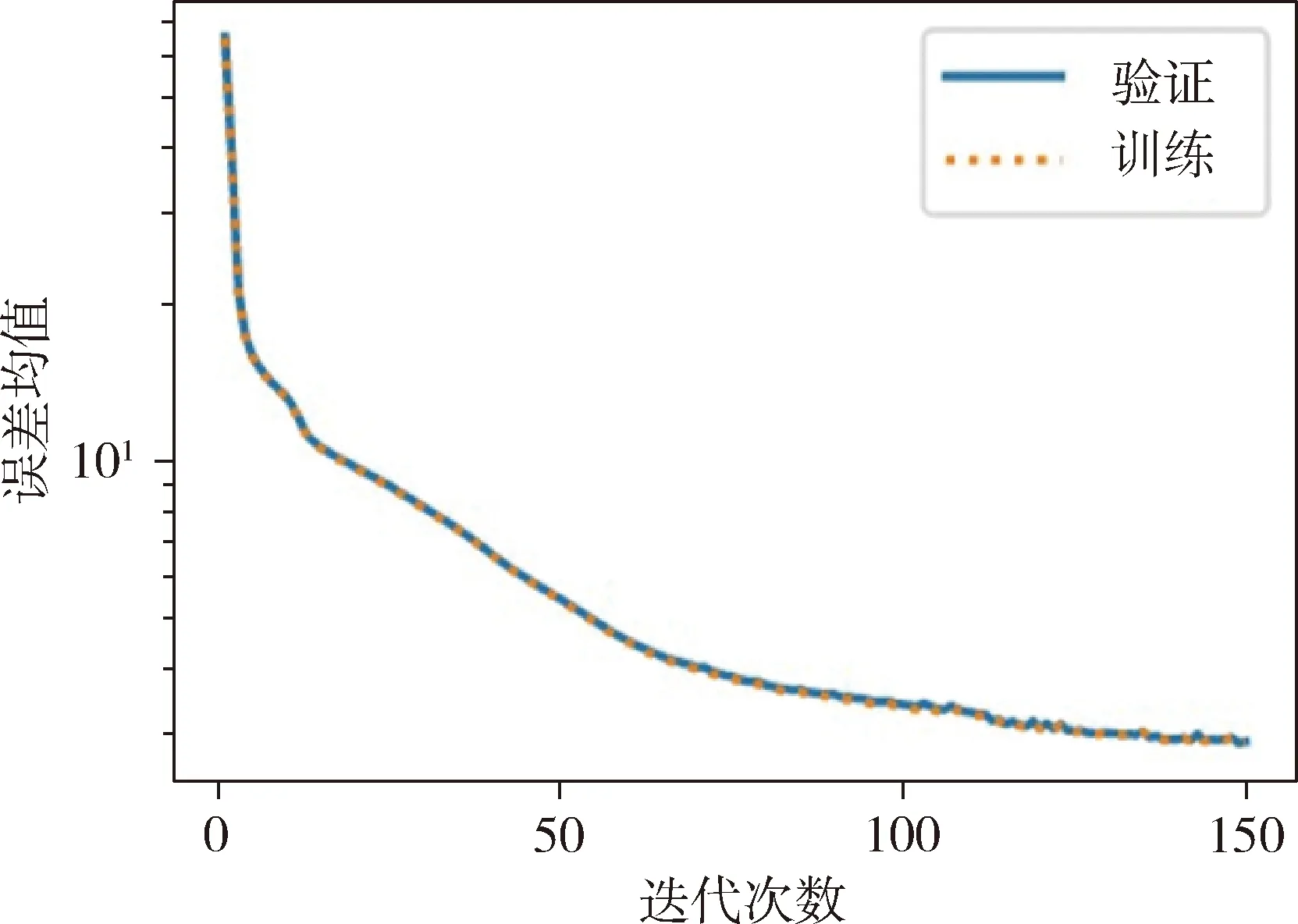
图8 网络最终训练结果Fig.8 Network training result
3 实验与结果
本节主要对提出的测姿方法,进行测量精度实验和算法的时间复杂度评估,验证算法的有效性和空间在轨工程应用的前景.
3.1 测量精度实验
应用预留的点云测试数据集,对训练后神经网络的姿态估计能力进行测试.在0°~180°范围内,用己知姿态的目标点云数据测试神经网络,如图9所示,模型对目标姿态估计的标准差为1.9°.
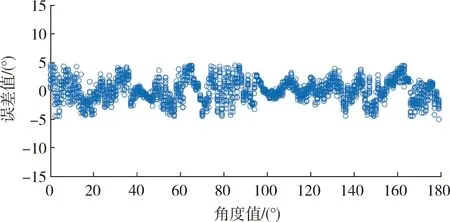
图9 模型对测试集的预测误差Fig.9 Test results for the network model
3.2 算法时间复杂度分析
经分析可知,本文提出的姿态测量算法估算目标点云姿态的核心步骤为:
1)计算目标点云的协方差矩阵;
2)神经网络参数的乘加计算.
因此,算法核心语句的执行次数与问题的规模无关,所以算法的时间复杂度为O(1).
对比传统的基于匹配技术的ICP方法,以及KNN算法,如图10所示,本文提出的姿态测量算法随着问题规模的增长具有时间复杂度低的特点.
为了定量比较不同算法的时间复杂度,对具有917个点的点云目标,在64位Windows 7 操作系统,Intel CPU 3.2 GHz主频,8 GB内存的计算平台下,对三种点云处理算法的执行时间进行了实测.每种算法均执行100次姿态解算,对每种算法的点云姿态解算时间进行统计比较,结果如表1所示,可以看到本文算法在计算时间上非常具有优势.
综上,本文提出的算法,在空间计算资源受限的条件下具有很好的在轨应用前景.
图10 不同点云处理算法的时间复杂度比较Fig.10 Time complexity of different algorithms

表1 算法时间复杂度定量比较Tab.1 Comparisons of algorithmic time complexity
4 结 论
针对当前空间非合作目标点云测姿态算法复杂度高、空间在轨计算资源受限,难以实现测姿态算法的在轨工程应用问题,本文提出一种基于点云特征建模的空间非合作目标姿态智能测量方法.该方法以特征建模思想为指导,实现了一种目标点云姿态的简捷高效表征算子,并在此基础上构建、训练了神经网络模型,验证了方法的实时性和有效性.实验结果表明,本方法具有计算复杂低、实时性好、适于在轨工程应用的特点.
致谢:
感谢吴宏鑫院士对本文工作的指导和帮助.在特征建模思想的核心内容、如何将特征建模思想应用到系统控制以外的其他领域、如何有效抓取研究目标的本质特征方面,吴宏鑫院士同作者进行了探讨并为本文提供了指导和帮助.

