具有抗噪性能适用高维数据的增量式聚类算法*

邵俊健，王士同

江南大学 数字媒体学院，江苏 无锡 214122

1 引言

聚类是机器学习和数据挖掘领域中的一种常用的数据分析工具，目前已被广泛地应用到生物、医学、交通等领域中。在过去的几十年中，有不少学者提出了各种各样的方法来解决不同场景下的聚类问题[1-2]。聚类方法是将具有一定规则的样本划分成具有同种性质的样本集的过程，没有先验知识的指导，是属于“无监督学习”的一种方法。聚类分析的内容包括系统聚类法、动态聚类法、图论聚类法等。20世纪80 年代由Bezdek 学者提出的模糊C 均值聚类算法[3]（fuzzy C-means clustering，FCM）成为一种经典的聚类算法，并且被有效地应用在数据分析、图像分割、数据挖掘等领域，具有实际应用价值和重要的理论指导意义。随着研究与应用的进一步发展，对FCM算法的研究也在不断丰富。

进入信息化时代以来，随着信息技术的不断发展，数据的不断累积，存放于数据库中的数据不断增多，对于大规模的高维数据的分析成为一个亟待解决的问题，这一问题在文献[4]中也曾被提及。如果对这些大规模高维数据依旧采用原始的聚类算法进行数据分析，可能会出现以下问题：（1）由于样本量过大，原始数据将会无法加载进入内存；（2）程序时间运行过长，严重占用计算机资源，降低算法性能等。针对以上问题，目前一般可以采用子空间聚类方法[5-6]、增量式聚类方法[7]来对大规模的高维数据进行有效的数据分析。

近年来，也有不少学者提出了许多不同的增量式聚类算法。李桃迎等人在文献[8]中对各种不同的聚类算法进行了简单的介绍。结合该文献和近年来提出的一些新的增量式聚类算法，大致可以将增量式聚类算法的几种改进方法分为：（1）在传统的聚类算法上进行改进；（2）在生物智能基础上进行改进；（3）对数据流的聚类算法。此外，Hore提出了单程模糊C 均值聚类算法[9]（single-pass fuzzy C-means，SpFCM）和在线模糊C 均值聚类算法[10]（online fuzzy C-means，OFCM）。Mei 等人在SpFCM 和OFCM 算法的基础上进行改进提出适用于对高维数据进行聚类的算法[11-12]。Wang 等人提出适合用于大规模数据集的多中心增量模糊聚类算法（incremental multiple medoids based fuzzy clustering，IMMFC）[13]。

FCM 算法是一种基于划分的聚类算法，在数据集存在异常数据的情况下，通常无法准确地对异常数据进行处理，亦就是说FCM 算法对噪声数据有很大的敏感性。研究者们通常对FCM算法的目标函数进行修改或者采用新的聚类算法，提出新的可以适用于并且有效处理含有噪声数据的算法。石文峰等人[14]通过扩展决策粗糙模糊集模型进行聚类的有效分析来确定FCM 算法的聚类数，可以避免初始化结果不好的缺点。刘沧生等人[15]在密度峰值聚类算法[16-17]的基础上，提出基于密度峰值优化的模糊C 均值聚类算法。该算法能更准确地得到聚类簇的数目，性能有明显的提高。前者是有明显的图像分割效果，后者相比于FCM 可以有更少的迭代次数和更快的效率，但是以上两种算法没有提及噪声或是高维数据对聚类算法产生的影响。陈加顺等人[18]提出的非噪声敏感性FCM算法能够有效克服对噪声的敏感性，从而提高算法的效率。该算法在人工生成的服从高斯分布的数据集上可以得到相对于FCM较好的聚类结果，但是没有考虑到将实验用于区间数据集上进行进一步的实验分析。张辰等人[19]结合样本加权的知识，在Zhang等人提出的改进可能模糊C均值聚类算法（improved possibilistic C-means clustering，IPCM）[20]基础上提出一种概率模糊聚类新算法。该算法虽然具有处理大量噪声数据的能力，但是在噪声少或没有的情况下，其聚类效果并不是特别明显。此外，该算法仅是在低维数据的情况下分析，没有考虑在含有噪声的高维数据集的聚类效果。武斌等人[21]为了克服广义噪声聚类算法（generalized noise clustering，GNC）[22-23]对于参数选择和运行该算法之前必须运行FCM 算法来获取参数的缺点，结合可能聚类算法（possibilistic clustering algorithm,PCA）[24]提出一种快速的具有更快速度和更高准确率的广义噪声聚类算法（fast generalized noise clustering,FGNC）。该算法可以很好地处理含有噪声数据，聚类准确性高且聚类时间更短，从文中实验来看，该算法没有处理高维机制下对聚类算法产生的影响。

为了克服FCM算法对初始化聚类中心敏感的问题以及高斯噪声在高维数据进行聚类分析时会产生的影响，本文使用文献[25]中提出的模糊（c+p）均值聚类算法（fuzzy(c+p)means clustering，FCPM）中的初始化聚类中心的方法。即通过FCPM 算法计算当前数据子块的聚类中心，并且将距离聚类中心最近的部分样本点加入到下一个即将进行聚类的数据子块中进行聚类。此外，使用一种适合于含有高斯噪声的高维数据的新的距离度量方式来减少高斯噪声在高维数据进行聚类分析时带来的影响，本文提出一种适用于高维数据且含有高斯噪声的聚类算法ANFCM(c+p)（anti-noise fuzzy(c+p)means clustering）。

2 相关工作

2.1 模糊C均值聚类算法

假设X=(x1,x2,…,xn),X是一个含有N个样本的集合，其中xk(k=1,2,…,n)表示集合X中的一个样本。FCM算法的目标是将这N个样本按照其固有的特征属性划分成c(1≤c≤N)类。Bezdek 定义FCM 的目标函数如式（1）所示：

其中，U∈Uf为X的模糊隶属度矩阵，V={v1,v2,…,vc}表示聚类中心，uik表示第k个样本属于第i类的隶属程度，||xk-vi||表示样本xk与vi的欧氏距离，m为模糊指数。通过式（1）和拉格朗日乘子法可以求出隶属度矩阵U和聚类中心V的迭代公式，如式（2）、式（3）。

对于模糊C均值聚类算法而言，需要满足以下三个条件：

在本文中由于篇幅原因，对FCM 算法的具体步骤和迭代计算不做详细介绍，该算法的基本思想可以参看文献[3]。

2.2 FCPM聚类算法

传统的FCM 算法对于聚类中心的初始化很敏感，常常会得到局部最优解，其聚类效果不是特别稳定。在FCPM算法中，采用将已知的一类固定来计算另一类的方法。在该方法下，某一类的聚类中心会吸引属于该类的样本，而排斥来自其他类的样本。

假设有c个聚类中心来自同一类，有p个聚类中心来自另外一类，FCPM 算法的任务是将这N个样本集合划分成c个类，其目标函数如式（4）所示：

式（4）中的uik与tjk需要满足式（5）的约束条件：

在式（4）中，Q=[q1,q2,…,qc]∈Rd×c，即Q为c个聚类中心所构成的矩阵。Z=[z1,z2,…,zp]∈Rd×p，即Z为已知的p个聚类中心所构成的矩阵。U=[uik]∈[0,1]c×N与T=[tjk]∈[0,1]p×N分别代表的是未知类和已知类的模糊隶属度矩阵。uik代表第k个样本xk与聚类中心qi的隶属度，tjk代表第k个样本xk与聚类中心zj的隶属度。

根据拉格朗日乘子法，式（4）在满足式（5）的约束条件下，可以求解得到模糊隶属度矩阵U和T以及聚类中心V的计算公式：

在文献[25]中，作者对FCPM算法的隶属度矩阵和聚类中心的解法进行了详细的介绍。此外，由于FCM 算法对于初始化聚类中心敏感性的问题，在该文中，作者通过FCPM算法初始化未知类的聚类中心V，依旧用原始的FCM算法初始化已知类的聚类中心Z，最后通过式（6）～式（8）迭代计算得到模糊隶属度矩阵U和聚类中心V，算法的具体步骤见FCPM 算法的描述。

算法1FCPM算法

步骤1设置一个空索引，记为l。

步骤2计算每个样本点的几何中心xmean=

步骤3计算各个样本到几何中心的距离，ak=||xk-xmean||,k=1,2,…,N。

步骤4找出距离几何中心最近的样本点xl1作为新的聚类中心加入集合A。

步骤5计算bk=ak||xl-xk||,k=1,2,…,N。

步骤6找出距离bk最远的样本点xl2作为第二个聚类中心加入集合A。

步骤7重复步骤6直至有c个聚类中心。

步骤8通过vk=xlk-0.1(xlk-xmean)计算聚类中心，其中k=1,2,…,N;l={l1,l2,…,lc}。该式中的系数0.1不是必要的，它可以加快聚类方法的收敛速度，并且减少边远数据的影响。

3 具有抗噪性能的增量式模糊聚类算法

3.1 ANFCM(c+p)

传统的FCM 算法对聚类中心敏感，导致一般的基于FCM算法的增量式聚类算法也有此问题。针对这一问题，文中使用FCPM算法中提及的一种新方法来初始化聚类中心。以往，原有的SpFCM 和OFCM算法都是通过WFCM（weighted fuzzy C-means clustering algorithm）算法进行加权，即通过赋予每个数据块的样本不同的权值来进行聚类，从而影响其聚类结果。但是数据块之间聚类中心的相互影响程度可能会由于上一次聚类结果的加入而影响聚类结果。本文不采用加权的方式赋予各个样本不同的权值，而是将经过上一次聚类的数据子块的聚类中心附近的部分样本点加入到下一个数据子块进行聚类。通过计算样本点到距离中心的距离，可以快速地获取需要添加到下一个数据子块的样本点。同时在算法的目标函数中添加一个相关项用来维持原数据块之间聚类中心的相互影响程度，其中β称为相关因子。当β=0 时，算法不考虑数据块间聚类中心的影响，仅仅考虑了某一数据块的聚类中心及其周围的几个样本点对下一个数据块的聚类性能的影响。当β≠0 时，既考虑数据块间聚类中心的影响，又考虑到某一数据块的聚类中心及其周围的几个样本点对下一个数据块的聚类性能的影响。在FCPM 算法中，uik与tjk需要满足式（5）的约束，为了能区别已知类和未知类在算法中的重要性程度，在原FCPM算法中的约束条件里加入一个判别因子λ，如式（9）所示。

在式（9）中，根据λ的不同取值，可以从以下两方面进行分析。

第一种情况，当λ=0 时，式（9）就变成了传统的FCM 算法的约束条件。根据前文中提到的FCM 算法对初始化聚类中心敏感性的问题，当λ=0 时，所提出的算法也会对初始化聚类中心敏感，因此在文中实验时，不对λ=0 这一情况进行讨论和分析。

第二种情况，当λ=1 时，式（9）即为原FCPM 算法的约束条件，即把c个未知类和p个已知类在算法中赋予相同的权值，不区分两种类的不同影响程度，与原FCPM算法无异。

结合以上分析，为了能更好地区分已知类和未知类的影响程度以及体现本文算法的优越性，一般实验的时候不考虑以上两方面所述。当λ值大于0且小于1 时，说明已知类在算法中的影响程度并不高，而当λ大于1 时，说明未知类在算法中的影响程度不高。

结合文献[26]在大量高维数据的实验场景中对各种不同距离度量的讨论，可以从其实验结果中看出余弦距离处理高维数据时能获得较好的结果。在文献[27-29]中，作者均指出余弦距离在高维海量数据集中能有效地度量样本之间的相似性。在高维数据中，随着数据维度的不断增加，数据将变得越来越稀疏，传统的欧式距离是用向量之间的间隔长度大小衡量距离，在面对高维数据时，通过其计算的相似性几乎是完全一致的，不能很好地判断两个样本之间的差异。余弦距离是通过计算两个向量之间的夹角来衡量两个样本之间的相似度。对于任意两个向量x=(x1,x2,…,xn)和y=(y1,y2,…,yn)，由数学知识余弦相似度为两个向量夹角的余弦，即：

根据文献[26]对余弦距离的描述，可以使用如式（11）所示的余弦距离公式。

对于一个数据集X={x1,x2,…,xn}，任取其中的两个样本记为X和Y，分别对这两个样本加入一定的高斯噪声ε1=(0,σ)和ε2=(0,σ)，其中0表示高斯噪声的均值，σ表示高斯噪声的标准差。设加入高斯噪声后的两个样本分别记为X′和Y′，其中X′=X+ε1，Y′=Y+ε2。分别计算在加入高斯噪声之后的两个样本在均值情况下式（11）的后半项的分子和分母，如式（12）所示：

根据数学期望的性质和加入的高斯噪声的特点，可以将式（12）化简得到式（13）：

那么，根据式（13）可以推出一个适用于含有高斯噪声的样本集的新的距离公式，如式（14）所示：

其中，Δ=ε2，Δ指的是所加入的高斯噪声的方差。

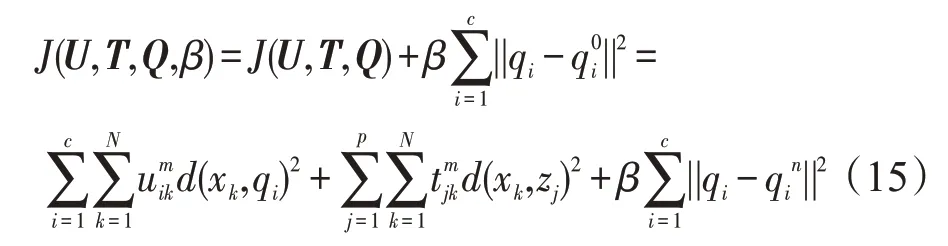
在式（15）中，uik是第k个样本相对于第i类的隶属度，qi是第i类的聚类中心，tjk是第k个样本相对于第j类的隶属度，zj是已知的p个类的聚类中心，是由FCPM算法计算得到的新的聚类中心。

采用拉格朗日乘子法对式（15）在满足式（9）的约束条件下求解新的隶属度矩阵U和T,新的聚类中心Q。

对式（16）中的P(U,T,Q,λk)的各变量分别求偏导并且令其等于0，得到式（17）所示的等式。

对式（17）求解可以得到隶属度uik和tjk以及聚类中心qi的计算公式（18）。

从式（18）可以看出，更新过后的模糊隶属度矩阵U和T与相关因子β的取值无关，更新过后的聚类中心qi在β等于0 或者不等于0 时又分为两种情况讨论。当β=0 时，从目标函数式（14）就可以看出忽略了数据块之间聚类中心的相互影响，为了能更好地提高算法性能，一般考虑β不等于0的情况。

3.2 算法实现

通过结合FCPM 算法中提及的新初始化中心的方法，给出ANFCM(c+p)算法的具体步骤。

算法2ANFCM(c+p)

输入：样本集X，未知类的类数c，已知类的类数p，模糊指数m，迭代终止条件ε，聚类中心临近点数a。

输出：隶属度矩阵U，聚类中心Q。

步骤1将样本集X根据不同增量比例随机划分成大小相等的t个子集，即X={x1,x2,…,xt}。

步骤2设置两个空集合Xnear和Xnew。Xnew用来存放每一个数据块产生的聚类中心，Xnear用于存放聚类中心附近的a个样本点。

步骤3依次循环对每一个数据块遍历获取聚类中心。

（1）初始化未知类和已知类的聚类中心Q和Z。

（2）将通过上一个数据块处理得到的样本集Xnear添加到当前数据块中，即Xc={Xc⋃Xnear}。

（3）通过式（17）计算当前数据块更新过后的隶属度矩阵U和T以及聚类中心Ql。

（4）将距离聚类中心Ql最近的a个样本点存入Xnew中。

（5）将聚类中心Ql及其附近的a个样本点存入Xnear中，即Xnear={Ql⋃Xnew}。

步骤4循环结束，得到隶属度矩阵U。

在步骤3 中，初始化聚类中心的方法是采用FCPM 算法来初始化未知类的聚类中心，采用原FCM 算法来初始化已知类的聚类中心。FCPM 算法的迭代停止条件为目标函数的连续变化值小于迭代终止条件ε，当所有子集数据块都遍历完毕获得最终的聚类中心Q和隶属度矩阵U时，整个ANFCM(c+p)算法结束。

ANFCM(c+p)算法通过FCPM 算法中提及的初始化聚类中心的方法和新的距离度量公式，用来对含有高斯噪声的高维数据进行聚类分析。此外，通过判别已知类的重要性程度和数据块的c个聚类中心及其附近的a个样本点作为辅助聚类信息加入到下一个即将进行聚类的数据子块中，从而来提高算法的聚类效果，并且保持算法良好的鲁棒性。

4 实验研究

为了对各聚类算法的聚类效果做出评价，本文采用归一化互信息（normalized mutual information，NMI）和兰德指数（rand index，RI）对算法性能进行分析。首先，为了分析加入不同样本点的个数对算法产生的影响，选择两个数据集进行简单的实验，主要分析不加入样本点和加入不同个数样本的ANFCM(c+p)算法的性能。其次，选择FCPM 算法、IFCM(c+p)（incremental fuzzy(c+p)means clustering）算法以及SpFCM 算法作为对比算法，将不同的噪声加入后与ANFCM(c+p)算法进行对比，从而验证算法的有效性。通过文献[9]对SpFCM 算法的介绍，可以计算SpFCM 算法的时间复杂度为O(ndT′c2)。通过文献[21]对FCPM 算法的介绍，可以计算FCPM 算法的时间复杂度为O(Tnd(c+p)+T′c)，其中T指的是算法迭代次数，n是样本数目，d是样本维度，c是未知类的类数，p是已知类的类数。由于FCPM算法不是增量式的算法，但是SpFCM、IFCM(c+p)和ANFCM(c+p)是增量式的，因此在其时间复杂度的计算中，需要对每个不同增量比例的数据块的迭代次数求其平均才是IFCM(c+p)和ANFCM(c+p)的时间复杂度，即O(T′nd(c+p)+T′c)，T′即为每个数据块的平均迭代次数。

4.1 评价指标

（1）归一化互信息（NMI）[30-31]

在式（19）中，N是指该数据集的样本总数，Ai指经本文聚类算法之后第i类的样本总数，Bj指真实数据集的第j类的样本总数，Ri,j是指第i类与第j类的共有样本总数。

（2）兰德指数（RI）[30-32]

在式（20）中，N为该数据集的样本总数，a指经本文聚类算法之后与实际类别信息中同类别的样本个数，b指经本文聚类算法之后与实际类别信息中不同类别的样本个数。

NMI与RI指标的取值范围均在[0,1]之间，其中当值越接近1 越能反映该聚类算法在某一数据集上的聚类效果越好，越靠近0时说明该算法在这一数据集上的聚类效果越差。

4.2 实验结果

4.2.1 实验环境

文中的实验在表1所示的实验环境中进行。

4.2.2 实验数据集

在实验中使用的数据集包括人脸表情数据集jaffe（http://www.kasrl.org/jaffe.html）、人脸数据库ORL数据集（http://www.cl.cam.ac.uk/Research/DTG/attarchive:pub/data/att_faces.tar.Z）、Coil 数据集、warp-AR10P数据集（http://featureselection.asu.edu/datasets.php）、Bin-alpha 数据集、MSRA 数据集（https://mmcheng.net/msra10k/）。各数据集的具体参数如表2所示。

Table 1 Experiment environment表1 实验环境

Table 2 Parameters of datasets表2 数据集的具体参数

4.2.3 实验参数设置

文中实验的参数设置为：模糊指数m取值为1.5，最大迭代次数max_iter取值为100，迭代终止参数min_impro取值为1E-3，在新初始化聚类中心方法（即FCPM算法）中距聚类中心最近的样本点n0取值为5，对各个数据集样本点在1 000 以下的数据集重复进行20次实验，对数据集的样本点在1 000以上的重复进行15次实验。由于是基于增量式方法的聚类算法，因此实验中每次加载进入内存的数据块大小是不同的。根据表2所示的数据集的样本总数，结合考虑IFCM算法初始化聚类中心的特点，分别对jaffe、ORL和Coil数据集样本总数的5%、10%、20%、25%、50%，对warpAR10P 数据集样本总数的10%、20%、30%、40%和50%，对MSRA 和Bin-alpha 数据集的1%、5%、10%、20%、25%和50%随机抽取进行增量聚类。由于MSRA 和binalpha 数据集的样本点无法合理地按照以上增量比例进行实验，在本文中一般随机选取MSRA数据集的1 700个样本点和binalpha数据集的1 400个样本点进行实验。在本文实验中，设置已知类p的值为按照不同比例进行增量的小数据块中最后一块的类的个数。例如，对于Coil数据集，当选取5%的样本进行增量聚类时，每一个数据小块的样本数是72，把最后一个小数据块即第1 369到第1 440 的样本的类别数目作为p值。此外，还对参数相关因子β进行参数寻优，其寻优范围分别在{0.1,0.2,…,1.0}。

4.2.4 算法性能比较

第一部分实验，选择Coil、jaffe两个数据集，在每次聚类时，加入不同个数的样本点到下一个聚类数据子块中。由隶属度矩阵计算得到的NMI和RI评价指标分析结果如图1和图2所示。

根据图1和图2的实验结果来看，在不加入样本点的情况下，在增量比例较小的情况下，其聚类效果比较好，但是当增量比例逐渐增大时，其聚类效果就低于加入样本点到下一个数据子块中去聚类的情形。总体来说，加入聚类中心附近的样本点到下一个要聚类的数据子块中进行聚类是可以得到较好的聚类结果。此外，加入不同个数的样本点同样也会对算法产生一定的影响。在不同增量比例时，样本点个数的加入也会有不同的结果。在文中加入聚类中心附近的样本点是为了考虑数据块之间聚类中心的相互影响。

第二部分实验，在表2所示的数据集上分别添加均值为0，标准差为0.3 和2.0 的高斯噪声后，将ANFCM(c+p)与非增量式的FCPM 算法、增量式的SpFCM 算法和IFCM(c+p)算法进行对比实验，计算经过以上4 个算法聚类得到的隶属度矩阵而得出的NMI和RI评价指标，如表3～表14所示，表中加粗的结果即是在文中所示实验环境下，模糊指数m为1.5时的结果。

Fig.1 NMI of Coil and jaffe with different samples图1 Coil和jaffe数据集加入不同样本点后的NMI值

Fig.2 RI of Coil and jaffe with different samples图2 Coil和jaffe数据集加入不同样本点后的RI值

从表中的实验结果可以看出，虽然FCPM算法在一两个数据集里得到的RI和NMI评价指标比较好，但是在大部分情况下，该算法相比于增量式的聚类算法的聚类效果并不是特别理想。随着维度逐渐增加，从表中实验结果看出ANFCM(c+p)算法具有良好的抗噪性能。在给样本添加高斯噪声后，ANFCM(c+p)算法的抗噪性能在大部分情况下是优于实验中三种对比算法的。而对以上数据集加入不同标准差的高斯噪声时，可以看出当高斯噪声的方差比较大时，ANFCM(c+p)算法在多数情况是能比其余三种算法得到更好的聚类结果。而噪声方差比较小时，三种不同的增量式算法都在不同增量比例时达到最好的聚类结果。在Coil数据集中，本文所提出的ANFCM(c+p)算法是完全拥有了良好的抗噪性能。当样本的数量比较多的情况下，无论是噪声方差比较大或较小的情况下，ANFCM(c+p)相比而言，更能得到良好的聚类结果。在表2所有的数据集中进行实验时，亦可以发现，随着样本增量比例逐渐增加至50%左右，其聚类效果一般是低于增量比例较小的数据块。这是由于，当增量比例较大的时候，进行聚类的数据块是趋向于对整个数据集进行数据分析，与传统的非增量式聚类算法没有差别，一般情况下，其聚类性能是比较低的。因此，在使用增量式聚类算法的时候，选择一个合适的样本比例是一个重要的选择。ANFCM(c+p)算法在使用新的距离度量时，考虑到新增加进来高斯噪声的影响，将这部分影响在进行聚类之前就将其减去，相比于传统的欧氏距离其聚类效果是有很大提升的。

Table 3 NMI of Coil dataset表3 Coil数据集的NMI 值

Table 4 NMI of warpAR10P dataset表4 warpAR10P数据集的NMI 值

Table 5 NMI of MSRA dataset表5 MSRA数据集的NMI 值

Table 6 NMI of Bin-alpha dataset表6 Bin-alpha数据集的NMI 值

Table 7 NMI of ORL dataset表7 ORL数据集的NMI 值

Table 8 NMI of jaffe dataset表8 jaffe数据集的NMI 值

Table 9 RI of Coil dataset表9 Coil数据集的RI 值

Table 10 RI of warpAR10P dataset表10 warpAR10P数据集的RI 值

Table 11 RI of MSRA dataset表11 MSRA数据集的RI 值

Table 12 RI of Bin-alpha dataset表12 Bin-alpha数据集的RI 值

Table 13 RI of ORL dataset表13 ORL数据集的RI 值

Table 14 RI of jaffe dataset表14 jaffe数据集的RI 值

5 结束语

本文从两个角度出发，一个是高维数据，另一个是含有高斯噪声的样本，提出了一种具有良好抗噪性能的ANFCM(c+p)算法。为了能有效地处理高维数据，该算法基于余弦距离度量进行改进用于处理含有高斯噪声的高维数据。余弦距离可以有效地对高维数据进行样本间相似性的计算，具有良好的鲁棒性。为了解决原FCM算法对初始化聚类中心敏感的问题，该算法使用FCPM 算法初始化聚类中心，综合考虑已知类和未知类在算法中的重要性程度，来有效提升含高斯噪声的样本的聚类性能。从第4 章的实验结果分析，文中提出的ANFCM(c+p)算法确实可以提高含有高斯噪声的数据集的聚类性能。文中两个值，相关因子β和约束条件式（9）中的λ是在实验中根据经验和大量参数寻优而得，而这两个值又是ANFCM(c+p)算法的关键所在，如何合适地选取是下一步的研究方向。根据文中实验结果的分析，选取一个合适的增量比例进行增量聚类也是一个可以研究的方向。此外，噪声的类别不只高斯噪声，还有如重尾噪声、拖尾噪声等，对于如何处理这些噪声也是一个可以继续研究的方向。