一种改进的图像消噪增强算法研究
宋建辉,樊思萌,于 洋,刘砚菊
(沈阳理工大学 自动化与电气工程学院,沈阳110159)
在传统的车辆识别系统中,一般从整幅图像中直接查找车辆,对于简单背景和较少干扰的车辆图像,利用图像分割技术可以比较好地分割出目标车辆;但对于具有复杂背景的车辆图像,直接提取目标车辆往往效果不佳。图像滤波能在某种程度解决这个问题,因为图像滤波能抑制图像噪声等细节的扰动,突出图像的主体,既可以对目标图像的噪声进行抑制,同时又能尽量保留图像细节特征。正是因为图像滤波的这种特性,使得其被大量应用在消噪增强等图像处理过程中。图像滤波也称图像平滑,分为线性滤波和非线性滤波两大类。线性滤波包括高斯滤波、均值滤波和方框滤波等,在图像消噪中得到广泛应用,但效率不高。文献[1-3]在考虑了图像像素强度之间的相似性和图像像素空间距离关系的基础上,提出了双边滤波算法这种非线性图像滤波算法,可以基本保持图像中各区域的分布,从而很好的保留了目标的边缘特征;不过该滤波算法对于图像背景滤波效果不佳,不能很好地抑制背景噪声,且该算法复杂度比较高。Xu L等[4]通过限制图像的像素梯度数量来对图像进行滤波,这种方法被称为L0梯度最小化平滑算法,通过该图像滤波算法可以获取良好的图像滤波结果图;但该算法会使所得到的图像边缘部分产生模糊,不利于后期处理。Zhang Q等[5]在研究了大量图像直方图信息的基础上提出了中值滤波算法,通过求取图像联合直方图中像素的权值,利用中值跟踪策略动态搜索邻域像素的中值,最后采用项链表工具实时采集直方图数据;该算法对图像滤波有效,但通过迭代控制平滑度,难以实现自适应。文献[6-7]提出了全变分平滑算法,该算法能够在约束条件和图像保真度之间找到一种平衡点,从而在去噪的同时保持图像的边缘;但该算法易将噪声误识别为图像边缘,使滤波后的图像产生假检,同时该算法会在滤波过程中改变图像的对比度。
为提高图像滤波后的视觉效果,在进行完图像滤波消噪后常需要对图像进行彩色图像增强处理。彩色图像增强是图像处理领域中的一个重要研究内容。近年来,彩色图像增强方法通常是基于色彩空间转换的,首先转换原始RGB图像致某个特定色彩空间下,然后使用灰度图像增强算法,最后将图像转换回到RGB色彩空间下,从而实现彩色图像增强。但这种方法对于各颜色成分的处理不能实现统一,因此此方法会使增强后的图像发生失真。1963年Land提出了Retinex理论,目前已出现多种改进的Retinex增强算法。传统Retinex图像增强算法对数域中直接将背景光照分量从原始图像中剔除,可以实现图像全局亮度和整体图像对比度的提升,但会减弱图像的局部对比度,且计算量也较大。
为更好地保留图像的边缘特征,提出了一种新的图像滤波算法。首先以图像像素强度和图像梯度作为约束条件,构造滤波函数的最优化方程,将图像处理问题转化为数学问题,采用变量分离和交替优化算法相结合的方式进行求解,并融合改进Retinex算法进行彩色图像增强。
1 本文算法流程
图像滤波消噪常运用在车辆识别的初始阶段。为能更好地使图像中车辆目标对象的边缘特征尽可能清晰准确的保留下来,提出一种改进的图像滤波算法,通过建立数学优化模型,将图像像素强度和图像梯度作为优化方程的约束函数,以此建立图像滤波算法,并融合彩色图像增强,步骤如图1所示。
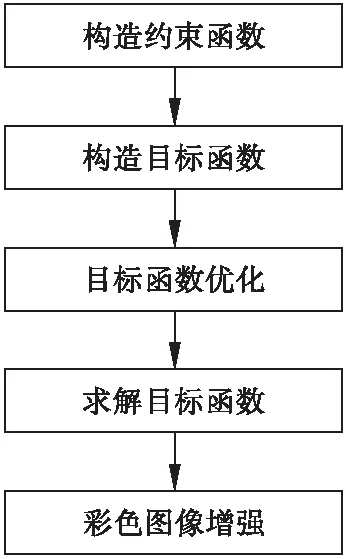
图1 本文算法流程图
首先构造以图像像素强度和图像梯度函数作为约束项的约束函数(这是因为图像滤波算法的作用是尽可能使经过滤波算法处理后的图像中目标对象的边缘更加清晰准确,模糊图像中非目标对象边缘区域的色彩,从数学角度上说,就是使得图像中非目标对象边缘区域的梯度变化为0。当图像矩阵中所有像素值为相同常数C时,则可以得到该梯度图像的梯度矩阵为零矩阵,既图像实现了完全滤波。根据这个理论,可以通过减少图像的梯度矩阵中非零元素的个数实现图像滤波算法);然后,构造图像滤波目标函数,图像像素强度和图像梯度为两个未知变量,所以在构造目标函数时要引入两个其它变量来代替这两个未知变量;由于目标函数引入了辅助变量,因此要在目标函数中人为加入两个惩罚因子,得到新的图像滤波目标函数;最后,图像滤波模型转变为求解这个新的目标函数最小化的最优数学问题;同时采用改进的Retinex算法改善图像的视觉效果。
2 图像滤波数学模型
2.1 图像滤波数学模型构造
假设原图像为A,如图2所示。图2中车辆为待提取目标,背景包含其它车辆、商店、行人等多种干扰信息。

图2 原图像
设滤波后的图像为B,则构造图像像素强度和图像梯度函数作为约束项。
P(B)=σ‖B‖0+‖B‖0
(1)
式中:B∈Rm×n为滤波后的图像强度;B∈Rm×n为滤波后的图像梯度;σ为人为引入的惩罚因子1,目的是保证图像像素强度和图像梯度之间的平衡关系。
构造最小二乘模型,使滤波处理后的图像B接近于原图像A,则目标函数为
(2)
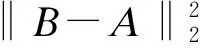

(3)
2.2 图像滤波数学模型求解
2.2.1 模型优化
运用半二次分裂思想[8]进行求解,引入两个辅助变量u和h=(hx,hy)T,分别代替约束项(3)中的B和B,同时引入两者误差的2-范数平方作为惩罚因子2,使辅助变量u和h逼近原图像像素强度和梯度,则滤波图像的方程重写为

(4)
式中β和χ分别控制辅助变量u和h与原图像强度变量B和梯度变量B的相似程度。
为更好地求解式(4),可采用变量分离和交替优化算法相结合,利用Matlab求解。将目标函数的l1成分(带未知量部分)和l2成分(不带未知量部分)解耦,l1正则优化问题简化为一系列非约束优化问题或常数。
2.2.2 算法分析

(5)

(6)
同理可解决关于u的最小化问题。将h和u带入式(4),求解滤波模型的最终解析解B,从而获得滤波后的图像。
3 改进Retinex彩色图像增强
3.1 经典Retinex算法分析
经典Retinex彩色图像增强理论的基本思想是光照图像和反射率图像的乘积等于原始图像,其数学表达式如式(7)所示。
S(x,y)=J(x,y)L(x,y)
(7)
基于Retinex图像增强的目的是对原始图像S中的光照L进行估计[11],以便对其进行分解,得到反射率图像J,从而消除不均匀光照因素对图像的影响,最终提高图像的视觉效果。为方便求解,将图像转至对数域[12],即s=logS,r=logJ,l=logL,则
logS=log(JL)
(8)
logS=logJ+logL
(9)
s=j+l
(10)
Retinex方法的核心是估测照度L,并去除L分量,利用式(7)得到原始反射分量J,既
l=f(s)
(11)
j=s-f(s)
(12)
3.2 Retinex算法改进
与降噪理论类似,Retinex算法的核心是合理假设图像的构成。即,假设人眼看到的图像是具有乘性噪声的图像,那么入射光的分量就是具有乘性的噪声。Retinex算法所做的就是正确估计图像中每个位置的噪声并将其去除。
在理想情况下,可认为整幅图像中的分量都是均匀的,那么估计照度L的最简单方式就是将图像变换为对数域后计算整幅图像的平均值。因此,对于Retinex算法改进的步骤如下。
(1)将图像变换到对数域,即s=logS;
(3)反变换到实数域,即J=exp(jlog255)。
在此基础上,还可对改进的Retinex算法进行补充,即通过使用引导滤波快速估计光照,可减少光晕的出现;另外,在完成Retinex算法处理后,可再对图像做gamma校正处理。后续实验表明,该方法色彩保持能力也有一定的提升。
4 实验结果与分析
利用构造的数学模型求解,并融入彩色图像增强,选取含有较多背景细节的汽车图像作为实验对象,图3为本文算法在取不同值时的图像滤波效果,由图3可以看出,α的取值与滤波程度有关,α值越大,图像越平滑,但过大会使得图像颜色失真。图4为多种效果图,由图4可以看出,当α取0.01时,本文算法效果最佳,与双边滤波的处理效果相似。图5为本文滤波算法在α取0.01时,融入彩色图像增强算法的效果图,由图5可以看出,在进行图像滤波后采用彩色图像增强能得到更好的图像视觉效果。

图3 本文算法效果图

图4 多种图像滤波效果图

图5 彩色图像增强效果图
通过主观视觉效果来衡量,本文算法滤波效果和双边算法滤波效果最好;彩色图像增强的目的主要是满足人眼观察的需要。本文选择计算图像标准差、均值和平均梯度三个客观参数指标来衡量图像质量的优劣。具体来说,图像均值与图像亮度呈正相关,图像均值越大图像亮度越大,反之越小;根据图像标准差与图像像素值和图像均值的离散程度,标准差越大图像质量越好;平均梯度与图像清晰度和纹理变化成正相关,平均梯度越大表明图像越清晰。表1所示为图像各种算法的客观性能比较,由表1可以得出,本文滤波算法和改进的Retinex算法对图像有较好的处理效果。

表1 图像客观性能比较
5 结论
提出了一种改进的图像滤波算法,通过建立数学优化模型,将图像像素强度和图像梯度作为优化方程的约束函数,构造图像平滑函数的最优化方程,将图像处理问题转化为数学问题,采用变量分离和交替优化算法相结合的方法进行求解,并融合改进Retinex算法进行彩色图像增强。实验结果表明本文算法处理图像具有良好的效果。

