凹形土质边坡降雨入渗研究的有限单元法
任德斌,张正涛,杨倩怡
(沈阳建筑大学 土木工程学院,沈阳 110168)
近年来,由于降雨造成浅层滑坡现象屡见不鲜,对人们的生产、生活造成了巨大的损失,从力学角度着手进行分析,主要是由于雨水入渗使得土体抗剪强度降低,从而导致滑坡[1]。学术界针对土质边坡降雨入渗的研究主要包括:有限元模拟降雨条件下边坡瞬态渗流过程[2];通过借助ABAQUS等有限元通用软件,来模拟不同降雨强度、不同土坡性质下的二维非饱和渗流,进而研究土坡稳定性问题[3];考虑因降雨引起边坡产生裂隙的原因,并对边坡稳定性进行分析[4];考虑地表径流与地下渗流耦合作用对入渗过程的影响[5]等。目前,针对土质边坡降雨入渗研究,主要采用二维简化模型进行分析,而忽略了边坡的三维效应,这就使得计算所得的地表径流深度不准确,同时,计算出的边坡安全系数与实际状况偏差较大,这对降雨入渗过程及边坡稳定性分析造成了一定的影响,最终会导致因工程建设的浪费而使工程成本增加或因对滑坡机制的误判造成重大工程事故。为了更深入的研究降雨滑坡问题,本文提出了一种考虑三维效应对地表径流及土坡边界条件影响的降雨边坡分析方法,为工程项目建设提供相关理论依据与合理化的对策建议。
1 非饱和土坡降雨入渗过程分析
非饱和土降雨入渗可以将其视为水平半无限空间的垂直入渗问题进行求解[6],入渗率是研究降雨入渗的重要参数,因此,在本文的研究过程中,将其视为关于时间的函数,二者之间变化关系如图1所示。
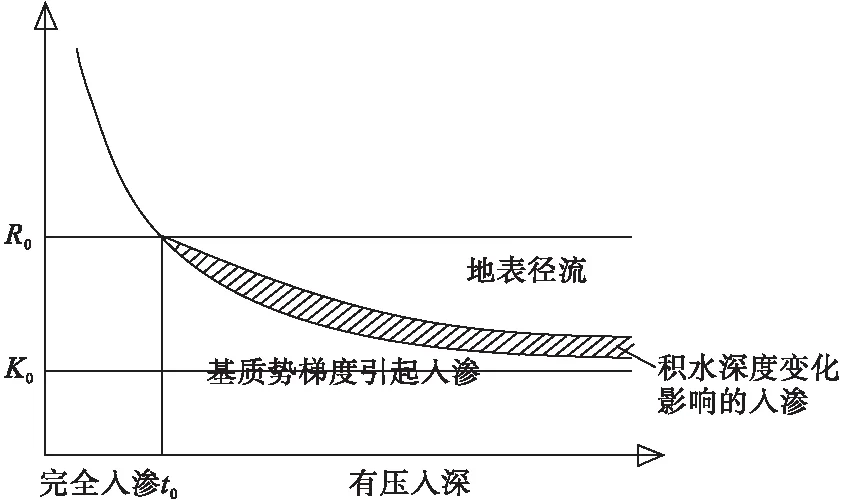
图1 稳定降雨强度下的入渗过程
从图1关系曲线可以看出,入渗过程大体上可以分为两个阶段,随着时间的推移依次经历完全入渗阶段和压入渗阶段,每一阶段都有其各自的特性。在雨水入渗过程中,土壤入渗率随着其饱和度的增大而逐渐减小[7]。以t0作为完全入渗与压入渗得临界时间,在t0之前,土壤的入渗能力较强,其远大于降雨强度,因此,该阶段的实际入渗率即可用降雨强度进行表示,渗流速度主要受供水控制,雨水全部渗入土体当中,降雨入渗处于完全入渗阶段。在t0之后,由于土体含水量较高,土壤入渗能力较t0之前有明显下降,此时降雨强度大于土壤入渗能力,所以该阶段的实际入渗率即为土壤入渗率,与完全入渗阶段不同的是此时雨水是部分入渗,另一部分,即超出入渗能力的部分则形成地表径流,渗流过程受到地表积水深度的动态变化及土壤基质势梯度二者共同影响,降雨入渗进入压入渗阶段[8]。
2 工程背景
2.1 工程概况
以杭州市某项目为例,该项目位于杭州市江干区牛田单元,地理位置隶属于杭嘉湖平原,根据地勘报告显示,该基坑属二级基坑工程,基坑开挖深度预计为20m,基坑开挖影响范围内土层主要为粉土,性质一般,土体自稳能力一般,透水性较强,在降雨条件下雨水水平渗流作用下边坡稳定性将会受到影响,严重时将会产生流土、管涌现象。
2.2 气象水文条件
据杭州市气象局近30年的统计资料显示:杭州市常年平均气温16.1℃,雨水充沛,降雨主要集中在在4~6月和7~9月,年平均降雨量达到了1400.7mm,日雨量大于25mm/d的天数达到16天左右,日雨量≥50mm/d天数为3.5天,日雨量≥100mm/d天数不到0.5天。该项目在基础工程施工期间降雨强度不大,但持续时间较长。
考虑到工程状况以及气象水文条件等因素,需要对土质边坡降雨入渗进行深入研究,并对边坡的稳定性进行分析,保证工程质量。
3 数值模拟的可行性分析
在进行凹形土质边坡降雨入渗及稳定性分析之前,需要进行数值模拟的可行性分析。首先,通过极限平衡法求解出降雨入渗条件下的安全系数,其次,建立有限元模型,模拟雨水入渗作用下边坡土体的失稳破坏形态,以收敛性作为确定安全系数的依据,以此得到数值模拟结果,最后将理论计算结果与数值模拟结果进行对比,以此来分析凹形土质边坡降雨入渗及边坡稳定性分析的数值模拟途径的可行性。
3.1 降雨边坡安全系数理论计算
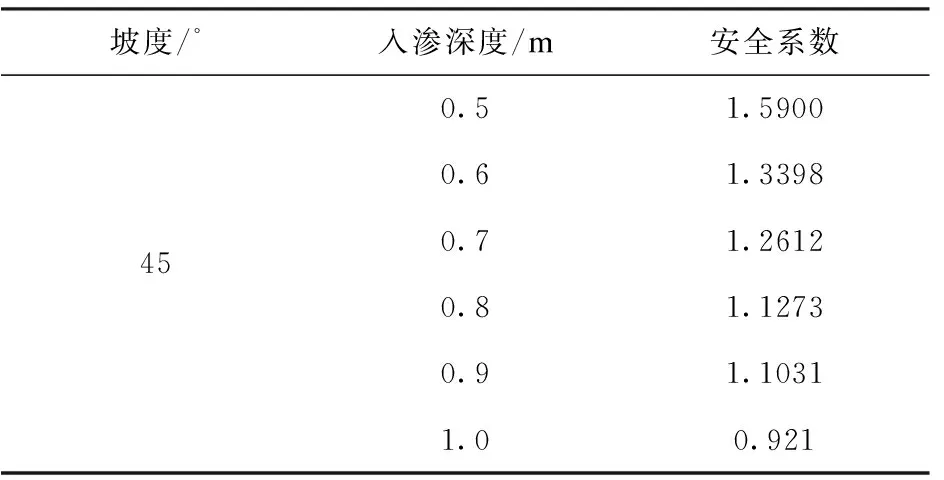
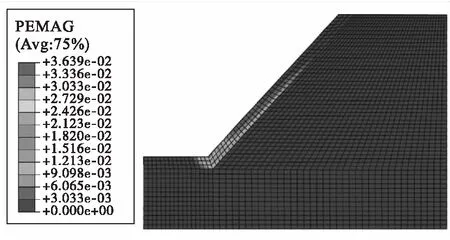
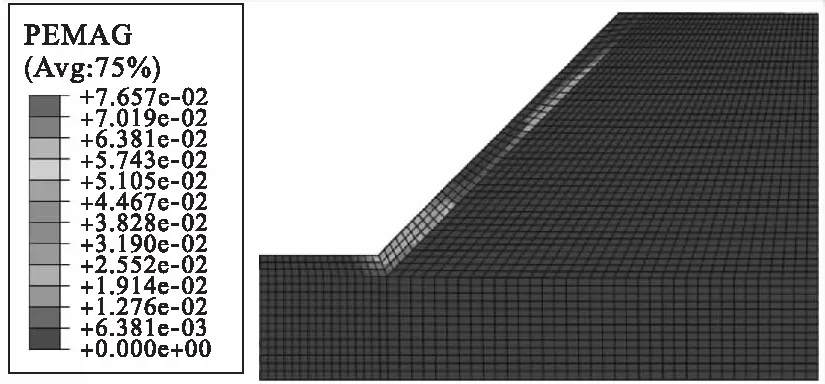
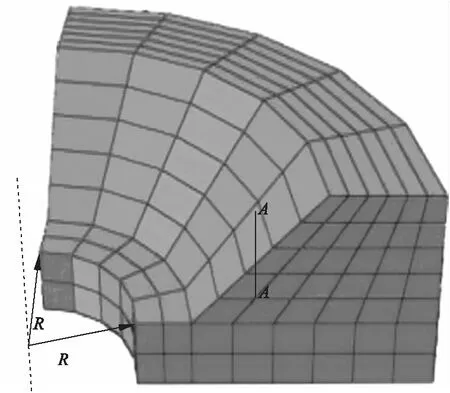
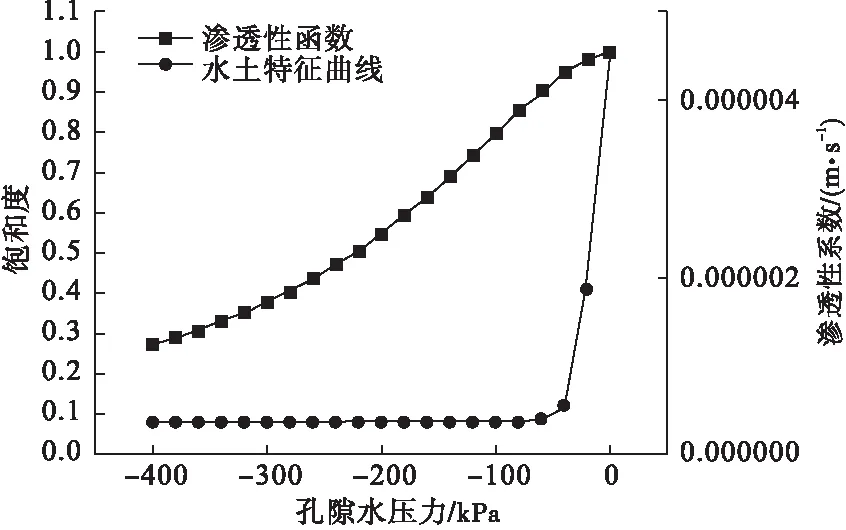
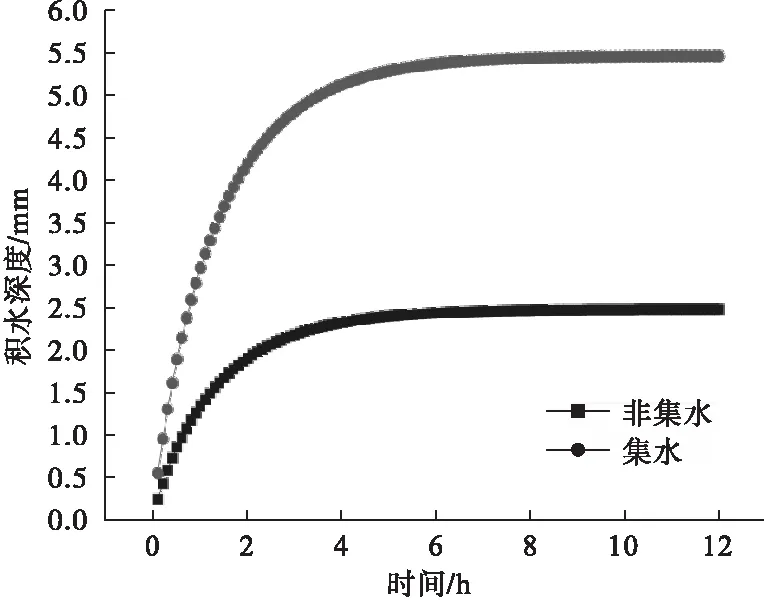
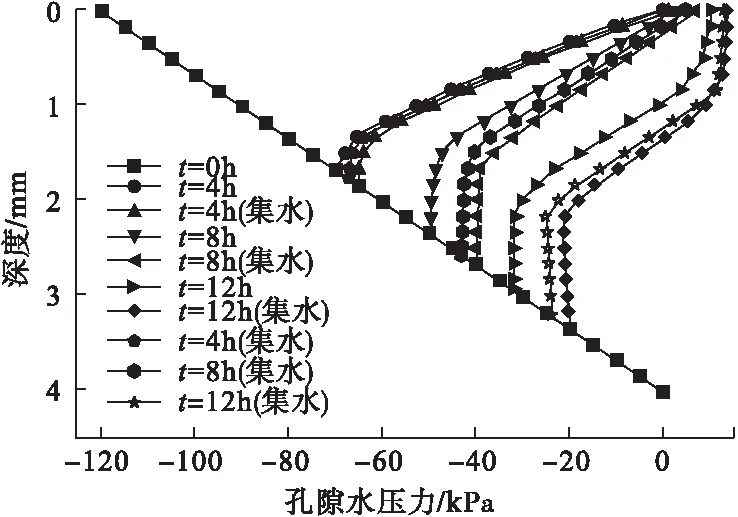
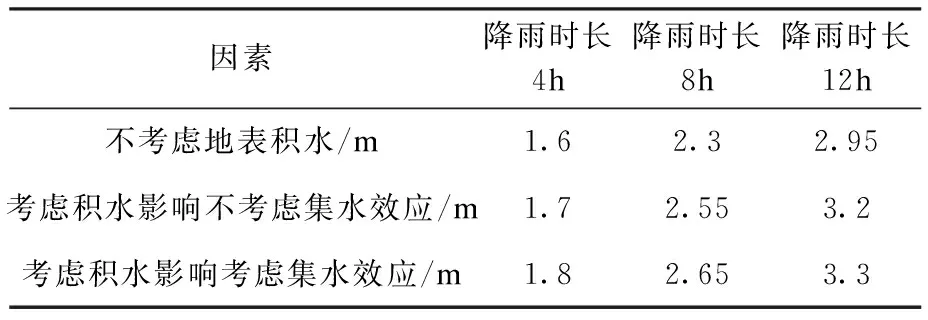
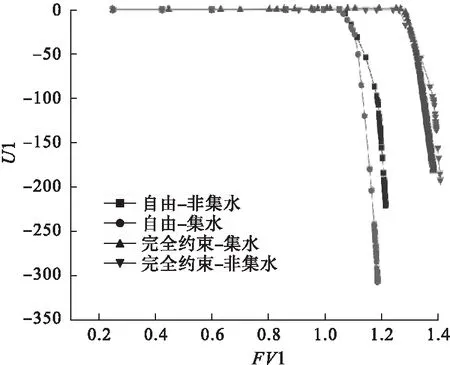
取边坡内单位厚度的平行四边形abcd作为一个土体单元来研究边坡土体的安全系数,即边坡的稳定性。土体中雨水的入渗深度为h,饱和的土层高度为mh(m为浸水比,且0 图2 边坡模型示意图 通过理论推导,最终得到了降雨情况下边坡安全系数Fs计算公式。 (1) 式中:τf为土体抗剪强度;τ为滑动面上的剪应力大小;γ为土体的容重;γw为水的容重;γsat为饱和黏土的容重;φ′为有效内摩擦角;c′为饱和土的有效黏聚力。 根据开挖范围内土体的相关性质,对土体的相关参数进行取值,取值如表1所示。 表1 土体参数取值 将土体的相关参数带入公式(1),可得到雨水渗入不同深度的所对应的安全系数,求解结果如表2所示。 表2 不同入渗深度对应的安全系数 通过理论计算可知,当雨水入渗达到1m深度时,边坡安全系数为0.921,安全系数小于1,说明边坡在此时发生失稳。 借助ABAQUS软件模拟雨水入渗作用下边坡土体的失稳破坏形态,以计算收敛作为边坡失稳的判定依据[9],至此得到了安全系数为0.8与0.9252时坡体塑形区开展状况,如图3和图4所示。 图3 Fs=0.8时坡体塑性区的开展状况 图4 Fs=0.9252时坡体塑性区的开展状况 通过图3和图4可以发现,边坡在雨水入渗条件下已经发生了塑形变形,塑形变形逐渐从坡脚向坡顶扩散,而且形成了一条贯通区,滑动面的位置也恰好与极限平衡法的假设一致。 进一步利用ABAQUS软件的数据处理功能,得到了折减系数Fs=0.9353,与极限平衡法中得到的安全系数相差0.0143.同时,通过有限元计算得到了折减系数Fs=0.9353时的边坡变形云图如图5所示。 图5 Fs=0.9353时的边坡变形云图 运用极限平衡法对安全系数的理论计算与ABAQUS的数值模拟,验证了数值模拟的可行性,对于后续研究地表积水与集水效应作用下的凹形土质边坡稳定性具有一定的可行性。 应用ABAQUS软件,分别对不同边界条件下考虑与不考虑地表径流和集水效应的降雨入渗进行数值模拟。在进行有限单元法的分析时,对模型进行了如下简化:(1)利用对称性,采用三维有限元模拟对边坡的稳定性进行分析;(2)现场施工对边坡的影响忽略不计; 同时,应该考虑模型与周围土体有一定的相互约束作用,以此对模型左右、前后以及基底各方向进行约束[10]。 模型计算过程中的相关参数如表3所示。 表3 土体参数取值 ABAQUS软件进行建模,构建出一个坡角为45°,坡高20m,坡长23.8m,边坡旋转半径R为30m,旋转角度为90°的边坡,如图6所示。 通过有限元结果分析,得到了水土特征曲线和渗透性函数如图7所示。 以降雨强度为50mm/h进行研究,降雨持续时间为0~12h,其日降雨量相当于暴雨水平,其小时降雨量为暴雨水平。三维边坡集水效应考虑与否对于最大径流深度的确定有较大的影响,至此,对A-A剖面处进行分析,得到地表径流积水深度随时间变化的关系曲线如图8所示。 图6 三维凹形边坡结构示意图 图7 渗透性函数及水土特征曲线 图8 坡面积水深度随时间变化曲线 由图8可知,在考虑集水效应与不考虑集水效应情况下,坡面积水深度均呈现指数增长,增长幅度逐渐降低,当达到3h左右时,坡面积水深度逐渐趋于稳定,同时,通过计算发现,考虑集水效应情况下的积水深度是不考虑集水效应情况下积水深度的2.2倍。 坡面径流深度主要受边坡形状、降雨强度、坡面粗糙度等因素的影响,在暴雨情况下,陡坡积水深度以毫米级进行计量,如遇到特大暴雨时,积水深度可能达到十几甚至几十毫米[2]。当降雨强度为50mm/h时,坡脚处剖面空隙水压力分布如图9所示。 图9 A-A剖面孔隙水压力分布 通过观察三种不同降雨时长雨水入渗过程发现,坡面积水在某种程度上直接影响降雨入渗深度,同时,三维边坡集水效应对入渗深度有一定影响,并且在考虑与不考虑三维边坡集水效应这两种情况下的深度差随着降雨的进行先增加而后逐渐趋于稳定,计算结果如表4所示。图10为FV1与U1的关系图。 表4 地表积水与集水效应下的雨水入渗深度 图10 FV1随U1变化关系 图10以出现唯一拐点作为降雨条件下土坡稳定的评价标准,边界条件采用自由边界与完全约束边界,以此来分析考虑集水效应与不考虑集水效应情况下边坡的安全系数,研究结果表明,考虑集水效应与否对于边坡安全系数影响较小,平均变化幅度为1.81%,但边界条件对于边坡安全系数影响较大,在考虑集水效应情况下,完全约束边界下边坡的安全系数远大于自由边界,安全系数提高了20.8%。 (1)在考虑三维凹形土质边坡集水效应对降雨入渗的影响过程中,随着雨水大量渗入土体,使得空隙水压力大幅提高,在水力梯度作用下浸润锋影响更深,并且在土层交界处其变化幅度较大。 (2)相同约束条件下,当考虑三维边坡集水效应时,边坡安全度略有减小,但影响程度较小,三维边坡边界效应对边坡的稳定性有显著影响,完全约束边界条件下的边坡,安全系数远大于自由边界下的边坡。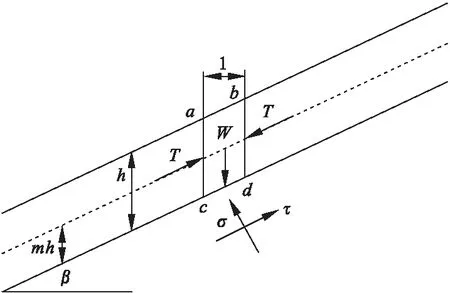

3.2 基于数值模拟的可行性研究

4 有限元模型建立
4.1 模型基本假设及基本参数确定

4.2 计算结果分析
5 结论

