基于RTDS仿真的最大功率点交叉检验的MPPT研究

王耀坤，姜志慧

（珠海市钰海电力有限公司，广东 珠海 519055）

0 引 言

光伏系统中，光伏板组成阵列可以被看作是直流电流电源，通常需要经过直流-交流（DC-AC）逆变器后再接入电网。光伏板的发电功率是由有效接收的太阳辐射决定的，由于太阳辐射等外界环境的变动性，需要采取最大功率追踪（MPPT）来跟踪最大功率点（MPP）。

目前，已有许多MPPT算法的研究，如固定步长法、扰动观察法（P&O）和电导增量法（INC）等[1-6]。基于C曲线的可变步长电导增量MPPT算法引入了变化因子，使步长根据距离MPP的远近而改变大小，可以在快速跟踪MPP同时减小MPP的震荡现象。然而，该算法也存在问题，当PV工作点接近并穿过MPP时，仍会引起明显的震荡现象，从而降低光伏系统的电能质量。

因此，本文通过实时数字模拟器（RTDS）仿真平台，改进设计并建立了一种具有最大功率点交叉校验（MPPcrosscheck）的可变步长增量电导MPPT算法，实现了高效和低震荡的MPPT算法目标。实时数字模拟器（RTDS）是专门为研究电力系统中的电磁瞬变而设计的设备，是由RTDS硬件和RSCAD软件组成，可以连续地计算出并给出近似代表实际电力系统情况的结果，实时仿真时间步长小[7]。

1 基本原理

1.1 基于C曲线的可变步长电导增量MPPT

由于受到光照、温度及遮蔽等外部环境的影响，PV电源的发电功率总在变动。因此，PV系统需要具有连续搜索并跟踪MPP的能力。MPPT基于光伏电源的P-V特性，是一种用于跟踪最大光伏功率的控制方案，通常由光伏系统的DC-AC逆变器来控制。该算法通过采样计算相关参数，控制逆变器，以确保系统达到最高的能量转换效率。MPPT的质量往往取决于跟踪MPP的效率、跟踪的震荡幅度以及外部条件变化时的跟踪速度。

电导增量算法可以快速地追踪外部环境的变动，并且具有相对较高的精度和稳定性。该算法根据PV特性曲线的斜率跟踪MPP，如果斜率为正，意味着PV工作点位于MPP的左侧，反之亦然。一种改进的可变步长电导增量算法，PV工作点距离MPP较远时步长取最大步长，距离MPP较近时取很小步长，既能快速跟踪变化，又能显著降低PV工作点在MPP的震荡。具体公式为：

其中，Vref为用于实现控制的参考电压。

基于C曲线的可变步长电导增量算法引入了C曲线：C曲线斜率的正负符号可以用于表示PV工作点距离MPP的远近。同时，根据PV曲线的斜率来确定步长Sk。其中Vref为参考电压、dVref为设定的最大步长。具体公式为：

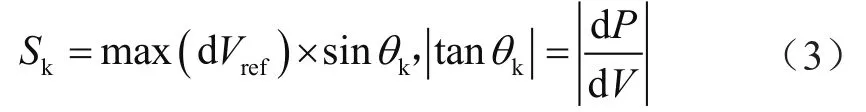
因此有：

1.2 仿真平台及算法建模

用于搭建算法的仿真平台为RTDS内建的PV系统模型，如图1所示。

图1 基于RTDS的光伏系统仿真模型

该系统是一个典型光伏系统，由13.2 kV三相输电线路连接的光伏模块、电网和动态负载组成[8]，拥有多个控制端口。在RTDS中构建控制算法并设置采样频率为40 Hz，最大步长为0.04 kV，C曲线中的N为1。

然而，源于C曲线MPPT的缺陷，实时运行中，PV在MPP附近工作时有明显的扰动和震荡。

1.3 基于C曲线MPPT的改进分析

当MPPT实时运行时，用于计算和条件检查的所有参数都依赖于直流电压Vk和光伏电流的采样，因此实际的PV曲线斜率和Vre曲线斜率是基于采样的近似值。为了方便分析，规定条件语句，如下所示：

其中，ΔVk=Vk-Vk-1,ΔPk=Pk-Pk-1,ΔCk=Ck-Ck-1。

当跟踪MPP时，很难精确地控制PV工作点使其正好落在MPP。因此，Vk和Vref会在MPP的左右两侧往复震荡。图2为PV工作点穿越MPP时的采样过程。

由图2可知，当PV工作点穿过MPP时，ΔVk的符号不变。然而，的符号无法确认，因为此时分别位于MPP的两侧，无法被视为斜率近似值，可以大于或小于从而导致步长的失序。

2 算法改进

2.1 MPP交叉检验

表1为PV工作点穿越MPP时的采样过程。

图2 PV工作点穿越MPP时的采样过程

表1 PV工作点穿越MPP时的采样过程

由表1可知，当PV工作点穿越MPP时，IF3k和IF4k输出的1或0的概率约为50%，这导致算法在MPP附近追踪时出现了约为50%的最大步长±max(dVref)，使参考电压Vref大幅来回震荡，进而导致光伏输出功率的大幅波动。为了改进上述算法，本文引入了MPP交叉检验（MPPcrosscheck），其定义如下：

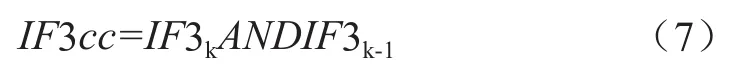
在最大步长算法路径前引入IF3cc，当PV工作点在MPP附近并穿越MPP时，能使步长保持在一个很小的值（Sk），可以避免出现大步长的失序现象。根据此原理，改进的MPPT算法的逻辑框图如图3所示。

图3 带有交叉检查的可变步长电导增量MPPT逻辑框图

2.2 MPP停止追踪算法

电导增量MPPT是一种不间断的追踪算法，由于控制系统本身的局限性以及光伏系统和外部条件的多重干扰，使得PV系统直流端的电压难以完全被追踪和控制。当MPPT在MPP附近工作时，被追踪和控制的直流回路电压会在MPP周围往复交叉移动。因此，加入MPP停止追踪算法（MPPstop）。综合MPPcrosscheck与MPPstop的MPPT算法的逻辑框图如图4所示。

3 仿真结果及分析

图5、图6与图7、图8分别展示了恒定光照强度（1 000 W/m2）下与光照强度阶跃变化（400～1 000 W/m2）时几种MPPT算法的仿真结果，其中横轴为时间t/s，纵轴包括PV直流输出电压VDCA8、PV直流参考电压VMMPA和PV直流输出功率Pin。

3.1 恒定光照强度（1 000 W/m2）

图5显示了固定步长MPPT的问题，其中在MPP附近往复追踪导致了电压和功率的震荡。如图6采用改进的带交叉检验的变步长MPPT算法，明显使震荡减小，显著提高了PV系统直流回路功率（Pin）的追踪精度和追踪效率。此外，图6比图5具有更高的平均输出电压及功率，同时消减了往复追踪带来的震荡。

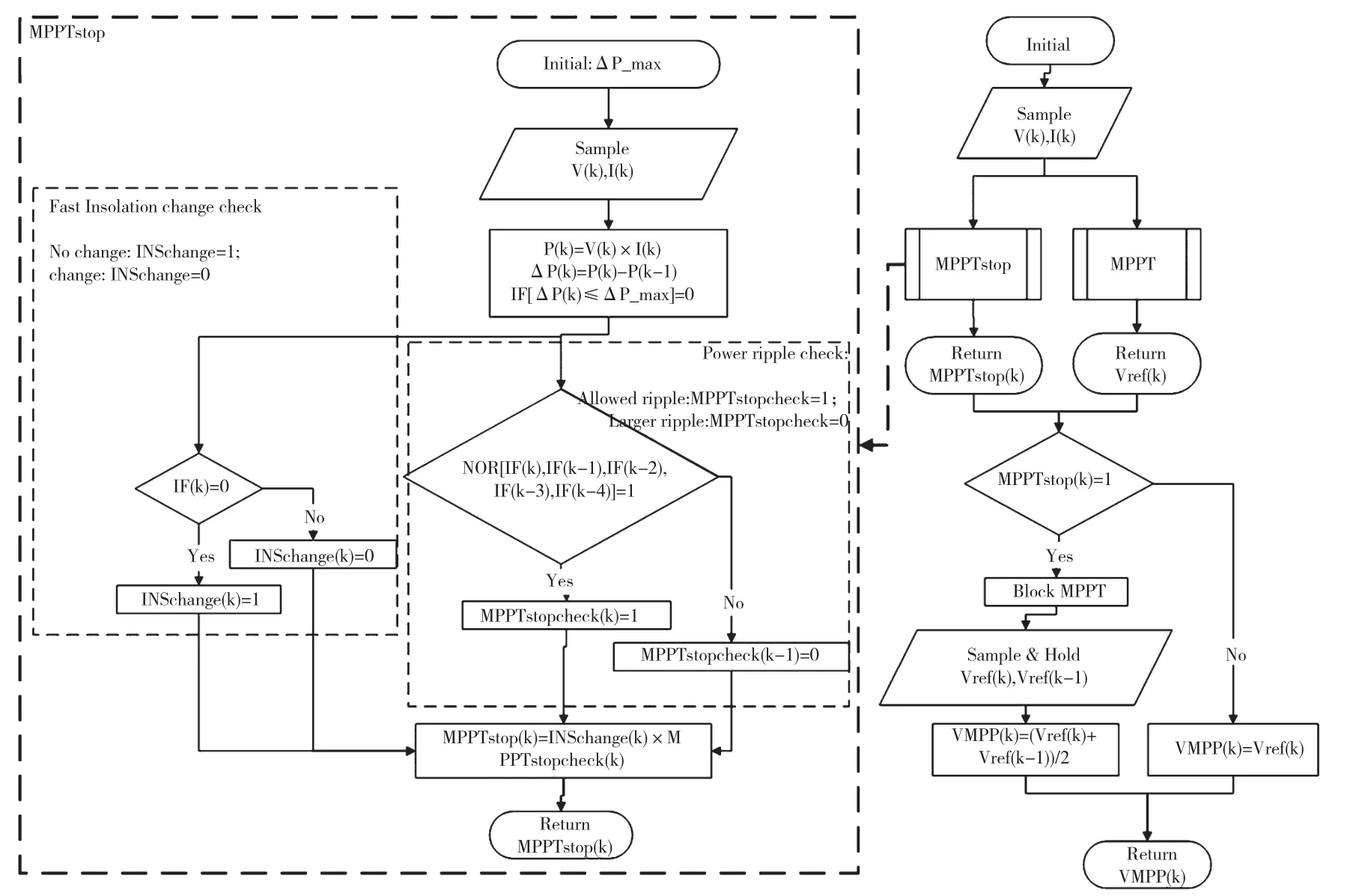
图4 MPPcrosscheck和MPPstop的全局结构逻辑框图

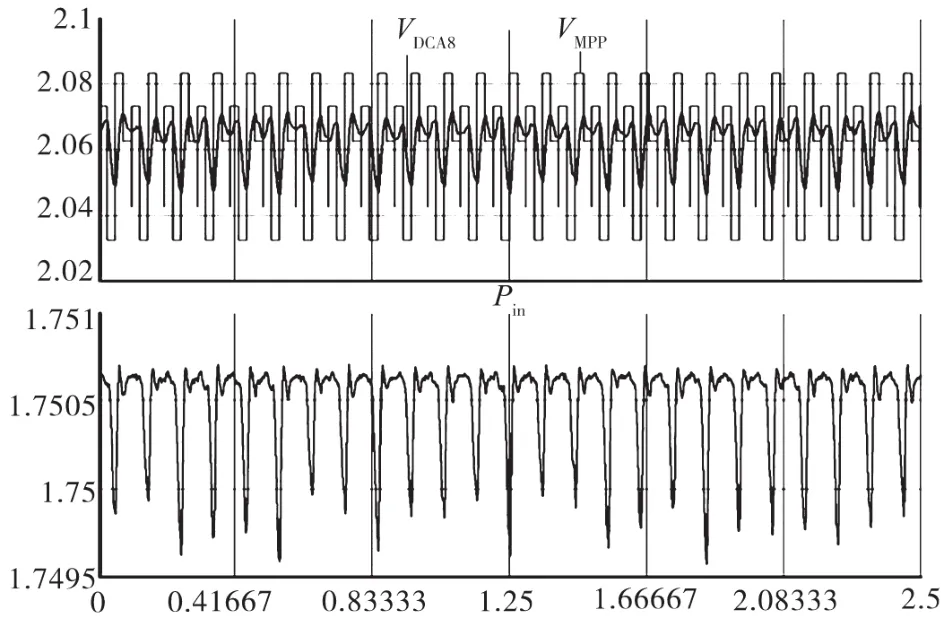
图5 基于固定步长MPPT的仿真结果（光强恒定）

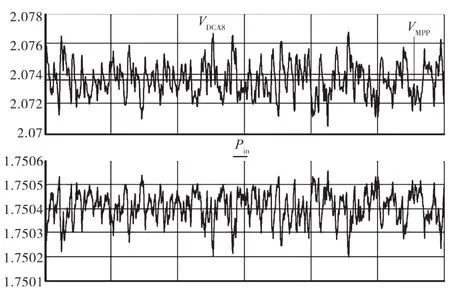
图6 带有MPPTstop和MPP交叉检验的MPPT仿真结果（光强恒定）

图7 基于固定步长MPPT的仿真结果（光强变化）

图8 带有MPPTstop和MPP交叉检验的MPPT仿真结果（光强变化）

3.2 光照强度阶跃变化（400～1 000 W/m2）

光强阶跃变化中，改进的MPPT算法相较于典型的固定步长MPPT算法，其PV直流回路电压能够更快接近光强变动后的MPP，同时电压的震荡幅度也相对较小，提高了PV系统追踪日照变化的效率。

4 结 论

通过基于RTDS的光伏系统的MPPT算法建模和实时仿真，引入了MPP交叉校验并改进了基于C曲线的MPPT算法，使系统在追踪电压并穿越MPP时保持微小的步长，同时MPP停止算法可以消除连续往复追踪MPP而引起的电压及功率的震荡。仿真结果表明，改进后的MPPT使PV系统直流端的输出性能有所提高，使其相较于经典的固定步长MPPT算法具有更小幅的功率震荡和更高的追踪效率。