基于加权社区检测与增强人工蚁群算法的高维数据特征选择

巫红霞 谢 强

1(镇江市高等专科学校装备制造学院 江苏 镇江 212000)2(南京航空航天大学计算机科学与技术学院 江苏 南京 210016)

0 引 言

特征选择是数据处理与模式识别领域的基础性研究，其性能直接影响分类器、模式匹配等应用的分类精度与泛化性能[1]。特征选择的目标是从特征集中选出判别性高、冗余度低的特征子集，降低数据集的维度，并降低不相关特征对数据分析的干扰，从而提高数据分析的效果与效率[2]。目前已存在大量有效的特征选择算法，并且已经成功地应用于低维数据领域[3]，但许多特征选择方法在高维海量或高维小样本数据集的处理过程中，存在计算开销过大或过学习的问题[4]。

在生物信息学、基因表达谱微阵列和图像识别等领域中，高维小样本数据容易引发“维数灾难”和过拟合问题，成为了亟待解决的难题。高维度导致计算复杂度高且分类器性能差，样本少则导致分类器学习效果差[5]。许多研究人员针对高维小样本数据提出了有效的解决方案，包括结合随机森林和邻域粗糙集的特征选择[6]、基于文化基因算法和最小二乘支持向量机的特征选择[7]、基于协方差估计多元回归的特征选择[8]等。为了提高特征选择的效果，文献[6]引入了随机森林分类与粗糙集计算，文献[7]引入了文化基因与最小二乘SVM，文献[8]则引入了多元回归模型等。这些算法对所有的特征进行高复杂度的运算，导致计算成本极高，难以运用于实际的工程应用。文献[9]的GCACO算法是一种性能较好的高维数据特征选择算法，该算法将特征分类，然后采用ACO(Ant Colony Optimization)算法对每个特征分类进行寻优处理。该算法将特征子集建模为完全图，导致模型复杂度较高。

减少冗余特征与不相关特征是特征选择的两个目标，许多研究将减少不相关特征作为目标，而忽略了冗余特征对分类性能的干扰[10]。特征选择主要可分为3类：过滤式、封装式和嵌入式，过滤式方法具有结构简单、训练速度快、独立于具体训练模型的优点。过滤式方法对于高维数据的计算速度快，因此本文采用过滤式方法。此外，本文算法同时将减少不相关特征与冗余特征作为研究目标，提出了无监督的高维数据特征选择算法。在特征选择过程中采用人工蚁群算法对特征进行了高效的寻优处理，提取出最优的特征子集。

1 特征选择的问题模型

常规的ACO算法一般基于完全图进行搜索处理，但文献[9]将特征选择建模为完全图，其算法复杂度较高。此外，因为特征选择问题的搜索空间有限，所以ACO算法容易陷入局部最优。许多高维特征选择算法并未考虑特征之间的冗余度。针对上述问题，本文设计了新的特征选择模型。

1.1 ACO的搜索空间表示

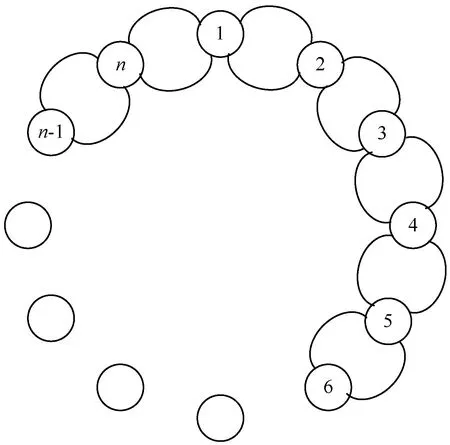
图1 特征选择问题的循环无向加权图

1.2 特征相似性评价

采用Pearson相关系数的绝对值评估特征之间的相似性：

(1)

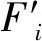
(2)

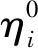
(3)

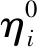
1.3 删除冗余特征

许多研究[12]通过计算当前特征集与之前特征集之间的相似性来选择冗余特征，但在一些特殊情况下，少量变化剧烈的特征导致当前特征集与之前特征集的平均相似性较低。为了避免该问题，从当前特征集中选出q个相关性最高的特征，计算q个特征与之前特征集的平均相似性。最终的平均相似性定义为：

(4)

式中:Γk为q个相似性最大的特征集；k为之前选择的特征集大小；l为之前选择的特征集。上述的每个特征集对应人工蚁群算法每次迭代所选择的网络节点集。

2 增强的蚁群优化算法与高维特征选择

2.1 增强蚁群算法的局部开发能力

为了防止蚁群在搜索过程中陷入局部最优，为蚁群算法引入两个随机算子与一个变异算子：(1) 随机位置(随机决定蚂蚁开始移动的节点)；(2) 随机方向(随机决定蚂蚁的移动方向)；(3) 节点变异。

受遗传算法的启发，设计了变异算子来增加搜索空间的状态数量，以防止发生早熟收敛。随机性算子与变异算子的实现方法为：ACO的第一次迭代将蚁群随机分布于图中各个节点；在每次迭代中，基于变异算子的条件交叉图中的指定节点，蚁群在新的图模型中游走。通过评估连续两次迭代的信息素改变率来决定是否应用变异算子，归一化的信息素改变率定义为：

(5)

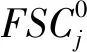
变异率决定了变异的发生概率，人工蚁群算法在早期阶段具有很强的全局搜索能力，在迭代过程中局部开发能力与收敛性逐渐提高。所以本文算法在第一次迭代的变异率设为最大值0.2，在迭代过程中逐渐降低变异率，从而在全局搜索与局部开发之间寻求平衡。

2.2 增强的蚁群优化算法

基于增强的蚁群优化算法(Enhanced Ant Colony Optimization,EACO)的特征选择算法如算法1所示。EACO的每次迭代中，将一个蚂蚁随机置于图中，然后，随机决定蚂蚁的移动方向(顺时针或者逆时针方向)。随后蚂蚁在循环图中游走，直至返回起点位置。一般情况下，信息方差大的特征包含的信息更为丰富，因此选择方差最高的特征进行状态切换。每个节点被蚁群选择与删除的次数定义为特征的状态计数器，每次迭代的结束阶段更新节点的信息素值(特征状态计数器)。在达到结束条件之后，选择信息素最高的特征作为最终的特征集。

算法1基于EACO的特征选择算法

输出：基于信息素排列的特征集

2. 计算启发式信息；

/*式(3)、式(4)*/

3. 节点的信息素初始化为常量τ0；

4. 创建startnodes与finalnodes两个列表；

5. foreachtfrom 1 toIter

6.mutationrate=0.2；

/*变异率初始化为1*/

7.mutationcondition=Phr(t)-Phr(t-1)；

8. ifmutationcondition>0

9. 图中的startnodes与finalnodes应用变异算子；

/*随机选择30%的节点，切换其状态*/

10.mutationrate=mutationrate-(0.2/Iter)；

/*变异率递减*/

11.FSCil=0；

/*初始化为0*/

12. 将蚁群随机分布于变异图上；

13. foreachjfrom 1 toAntsdo

14. 随机决定蚂蚁的方向；

15. 蚁群保持移动；

16. 蚁群根据状态切换规则选择或者取消一个节点

/*式(6)*/

17.FSCis=FSCis+1；

18. 计算信息素改变率；

/*式(5)*/

19. 更新信息素值；

/*式(9)*/

20. 基于FSC将startnodes与finalnodes两个列表分别设为最优节点与最差节点；

21. 特征集按信息素降序排列。

2.3 特征的状态切换规则

特征的状态切换规则定义为：

(6)

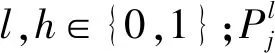
(7)

如果γ大于θ，那么应用概率规则：

(8)

式中:γ0为一个随机值。

2.4 EACO的信息素更新策略

每次迭代需更新每条边的信息素，EACO的信息素更新策略定义为：

(9)

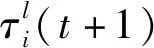
3 基于社区检测的并行特征选择方法

人工蚁群算法的求解效果较好，但是计算成本较高，因此设计了基于社区检测的并行特征选择方法。通过加权社区检测技术将特征集分类，对每个分类分别采用EACO并行地选择特征集，然后设计了全局的竞争机制处理所有分类的最优特征，选出全局最优的特征集。本方法同时提高了特征选择的性能与计算效率。

3.1 基于加权社区检测的特征分类

社区检测算法通过最大化模块化函数实现对节点的分类处理，社区检测算法的实现简单、性能较好，但是并未考虑特征子集之间的判别能力差异，因此本文设计了加权的社区检测算法。图2为特征集的社区检测示意图。

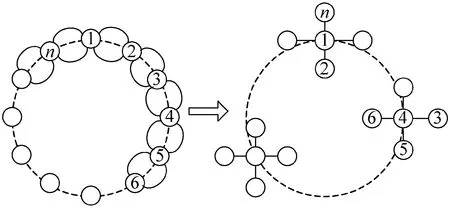
图2 社区检测的示意图

(1) 模块度函数。模块度函数评估社区划分的质量，定义为社区内部的总边数与网络中总边数的比例减去一个期望值。该期望值是将网络设定为随机网络同样的社区划分所形成的社区内部总边数和网络总边数的比例。假设一个加权网络共有N个节点与L条边，若将网络分为c个社区，那么模块度函数Q定义为：

(10)

式中:A为邻接矩阵，Axy={0,1}，1表示节点x与y之间存在一条边。Pxy为x与y之间边的期望值，Cx与Cy分别为x与y的社区，δ函数定义为：

(11)

一般通过配置模型计算边的期望值，定义为Pxy=kxky/2L，kx与ky分别为节点x与y的度。据此将式(10)改写为：

(12)

网络的总模块度定义为节点对每个社区的模块度之和：

(13)

式中：li为社区i中边的总数量；di为社区i中节点度的总和。因此eii=li/L为社区i中边的分数，ai=di/2L为至少一个端点在社区i中的边分数。

(2) 加权的模块化函数。通过最大化模块度的社区检测算法存在分辨率的问题，传统的模块度方法计算所有社区的模块度qi之和，将所有社区的贡献度视为相等。该方法倾向于将小社区组成大社区，从而实现较高的模块度。而在高维数据特征分类的应用场景中，基于相似性将特征分类，但相似性并未反映特征的判别能力，因此传统的模块度社区检测算法无法直接处理特征分类问题。

为了解决上述问题，通过为模块度函数引入一个权重项来区分强弱社区。加权的模块度函数定义为：

(14)

(15)

式中：Qw为网络的加权模块度；ni为社区i的节点数量。权重λi反映了社区的强度，即社区中边与最大值的比例，λiqi表示社区之间的相似度。权重λ的作用是确保强连接社区的贡献度被分配较高的权重，而弱连接社区的贡献度被分配较低的权重。

(3) 最大化加权模块度的社区检测。首先，将网络的各个节点设置一个社区，网络节点总数量为N则设置N个社区。然后，采用贪婪策略遍历每个社区，将两个社区合并，如果合并后的加权模块度提高，那么产生新的社区划分结果。重复该迭代过程直至获得最大的加权模块度。

如果社区i与社区j合并，合并后的加权模块度增益表示为：

ΔQw(i,j)=λcom×qcom-[λi×qi+λj×qj]

(7)

式中：qcom与λcom分别为合并后新社区的模块度与权重。每次迭代的社区节点总数量ncom、总度数dcom、边数lcom、总权重λcom、模块度qcom的计算公式为：

(8)

在每次迭代的结束阶段，将矩阵的第i行替换为更新后的指标值，即ni=ncom、li=lcom、di=dcom、qi=qcom、λi=λcom。算法2为基于贪婪加权模块度的社区检测算法。

算法2基于贪婪加权模块度的社区检测

/*网络图*/

/*最优社区划分结果*/

2. 计算网络参数n,d,l,lext,Q,Qw；

4. foreachcfromNto 1 do

5. foreachi,j∈{1,2，…,c} do

6. 式(7)计算u、v的模块度增益；

7. end for

10.Qw=ΛTQ；

/*Λ为权重向量，Q为模块度向量*/

13. end if

14. end for

(9)

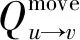
算法3社区检测的局部优化程序

/*最优社区划分结果*/

1. 计算网络参数n,d,l,lext,Q,Qw；

3. foreachu,v∈{1,2,…,N} do

4. 式(9)计算u、v的模块度增益；

5. end for

9. goto 第3行；

10. end if

3.2 并行队列的特征选择

每次循环提取每个特征类(队列)的top-k特征；然后，应用EACO处理所选的特征子集，从中选出K0个最优特征。然后对剩余的特征队列重复该过程，直至选出期望数量的特征子集。虽然该步骤重复了nf/K0次，nf为选择的特征数量，但其时间成本远小于处理全部特征的情况，并且蚁群算法对于子图的处理时间远小于处理全部特征的初始图。图3是并行队列的特征选择流程图。

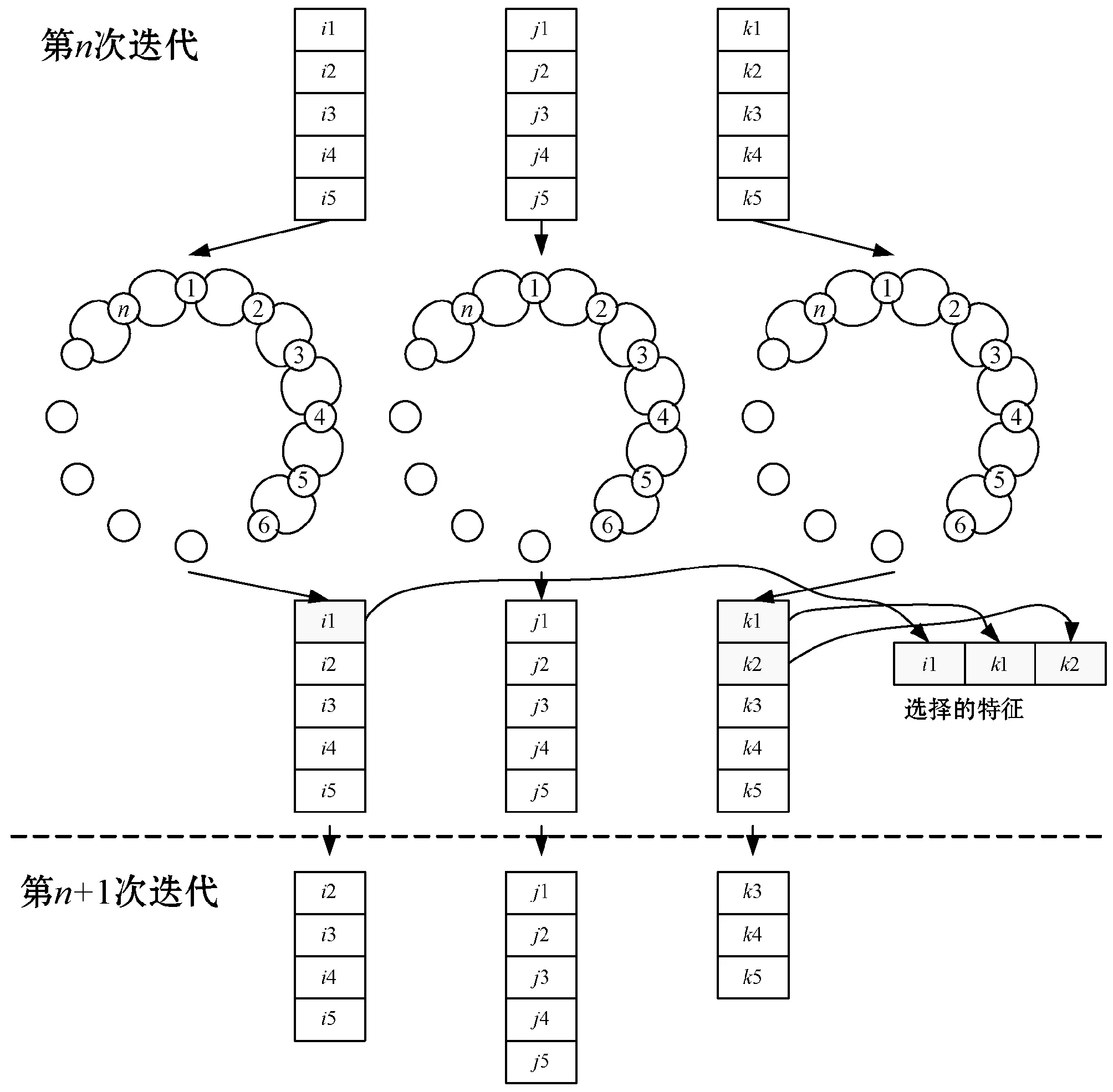
图3 并行队列的特征选择流程图(K0=3)

算法4为并行队列的特征选择算法。算法的第1、2行为并行的特征选择处理，通过EACO处理每个分类，获得特征队列。第4～8行的循环体迭代地从每个队列中选出全局最优的特征子集。

算法4并行队列的特征选择算法

/*降维的数据集*/

1. 特征分类；

2. EACO处理每个特征分类，获得特征队列；

3.k=nf/nc;K=K0；

4. foreachifrom 1 tokdo

5. 从每个队列中选出top-K特征集FK；

6. 根据信息素从FK中选出top-K特征子集；

7. 更新特征队列；

8. end for

为了实现全局地特征比较，应当将每个队列的信息素做归一化处理：

(13)

式中：τijl为类j中特征i的信息素；l=0与1分别对应该特征被选择与删除；LCj为类j的特征数量；n为特征的总数量；nc为分类的数量。

4 仿真实验与结果分析

实验的硬件环境为Intel Xeon CPU E5- 2650 v3@2.3 GHz处理器，软件环境为Ubuntu 16.04 LTS操作系统。采用C++语言编程实现相关算法。

4.1 实验数据集

实验采用两组公开数据集，第一组为UCI数据集，表1为UCI数据集的基本属性。第二组为高维数据集[13]，表2为高维数据集的基本属性。

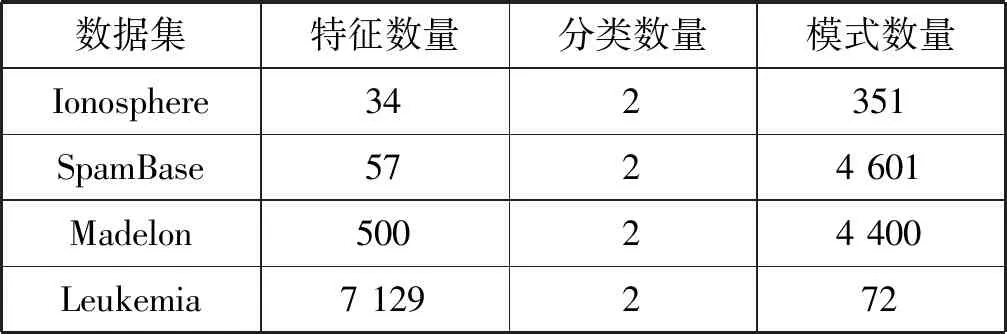
表1 UCI数据集的基本属性

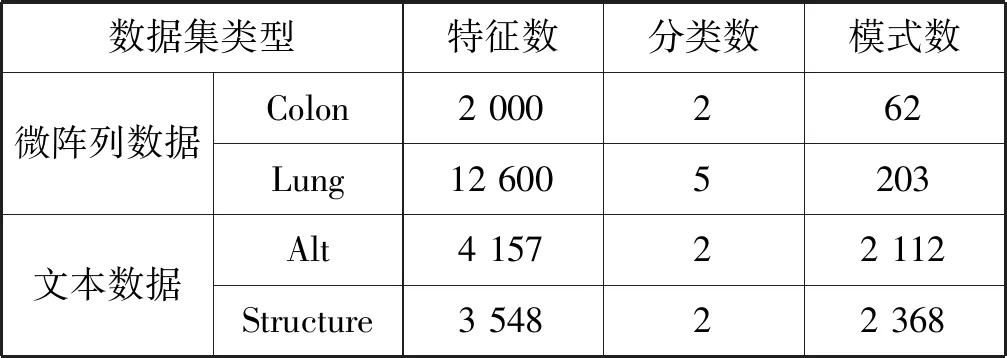
表2 高维数据集的基本属性

4.2 分类器与性能评价指标

(1) 分类器选择 本算法是一个过滤式特征选择算法，一般将过滤式特征选择算法与分类器结合，通过分类的性能评价特征选择算法的性能。为了排除不同分类器的影响，采用四种常用的分类器进行实验，分别为SVM(支持向量机)、DT(决策树)、KNN(k-近邻分类器)、RF(随机森林分类器)。

(2) 性能评价指标 根据文献[14]，分类误差率CER是评价特征选择算法的有效指标，CER值越小表示分类性能越高，CER定义为：

CER=错误分类的样本/样本总数量

(15)

4.3 仿真参数设置

蚁群算法的最大迭代次数设为50，信息素挥发率设为0.2，信息素初始值设为0.2，变异特征的概率设为30%，蚁群规模设为数据的特征数量，如果数据集的特征数量大于100，统一将蚁群规模设为100。

4.4 分类器性能的结果

本文采用K-折交叉检验评估分类器的性能。本算法与其他无监督的过滤式特征选择算法比较，分别为HGSA[15]、FSHD[16]和BGWOFS[17]。其中：HGSA也采用了与本文算法相似的人工蚁群优化；FSHD是一种新颖的高维数据特征选择算法，采用正则化机制对高维度冗余做惩罚处理，通过反馈机制学习优质的特征子集；BGWOFS则是一种基于灰狼优化算法的特征选择算法。

图4-图7分别为SVM、DT、KNN、RF四个分类器的特征选择结果，每组实验独立地重复10次，计算10次CER值的平均值与标准偏差作为统计结果。从图中可看出，本算法对于SpamBase、Madelon两个模式数量较多的数据集实现了较好的分类性能，其结果优于其他三种算法。此外，本算法那对于特征规模较大的Leukemia数据集表现出了较高的分类性能，明显地优于其他三个算法。最终，本文算法对于四个不同的分类器均表现出较好的分类效果，说明本算法选择的特征集具有较好的判别能力、较低的冗余度与不相关性，并且具有较高的稳定性。

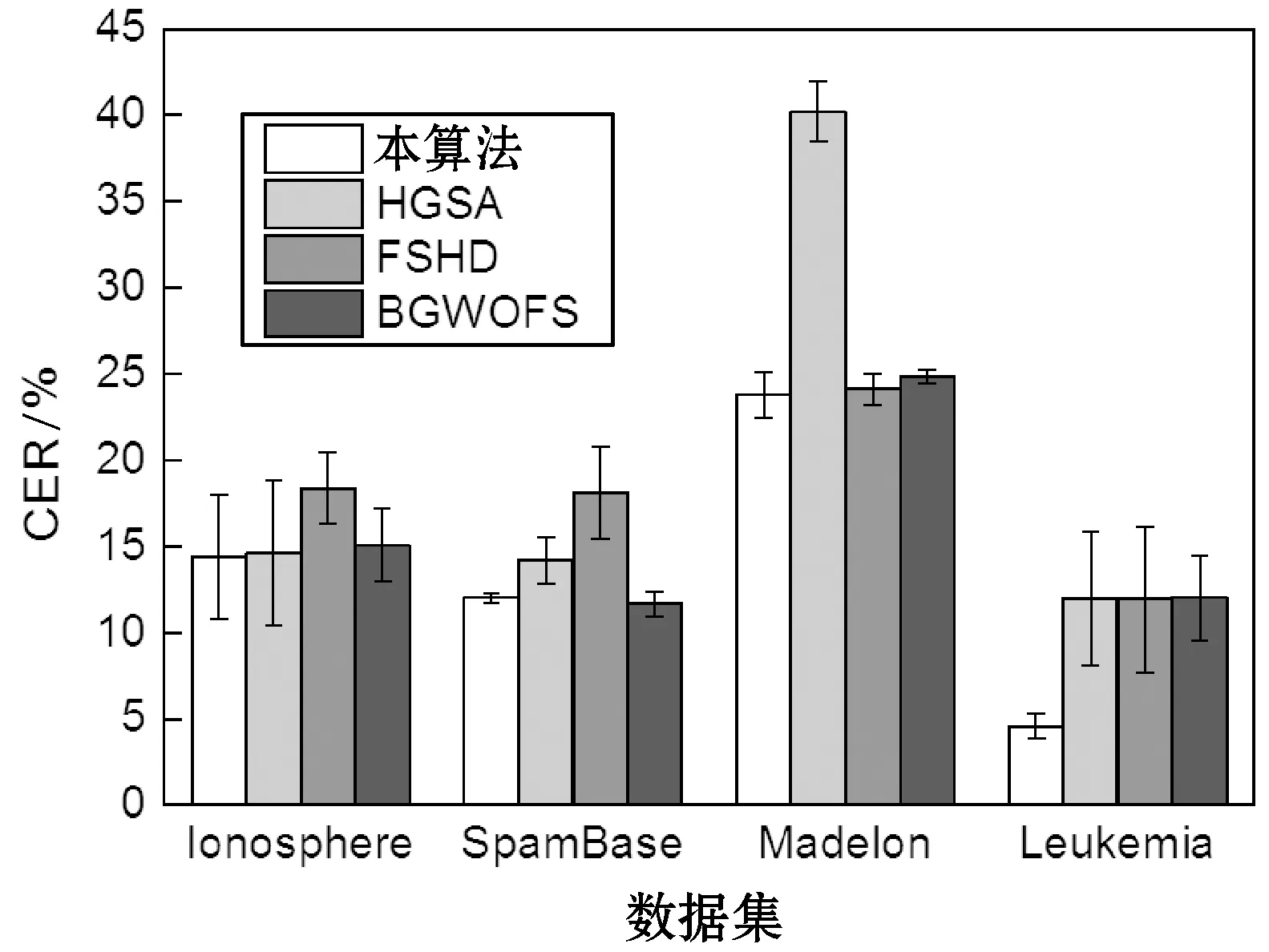
图6 KNN分类器的结果

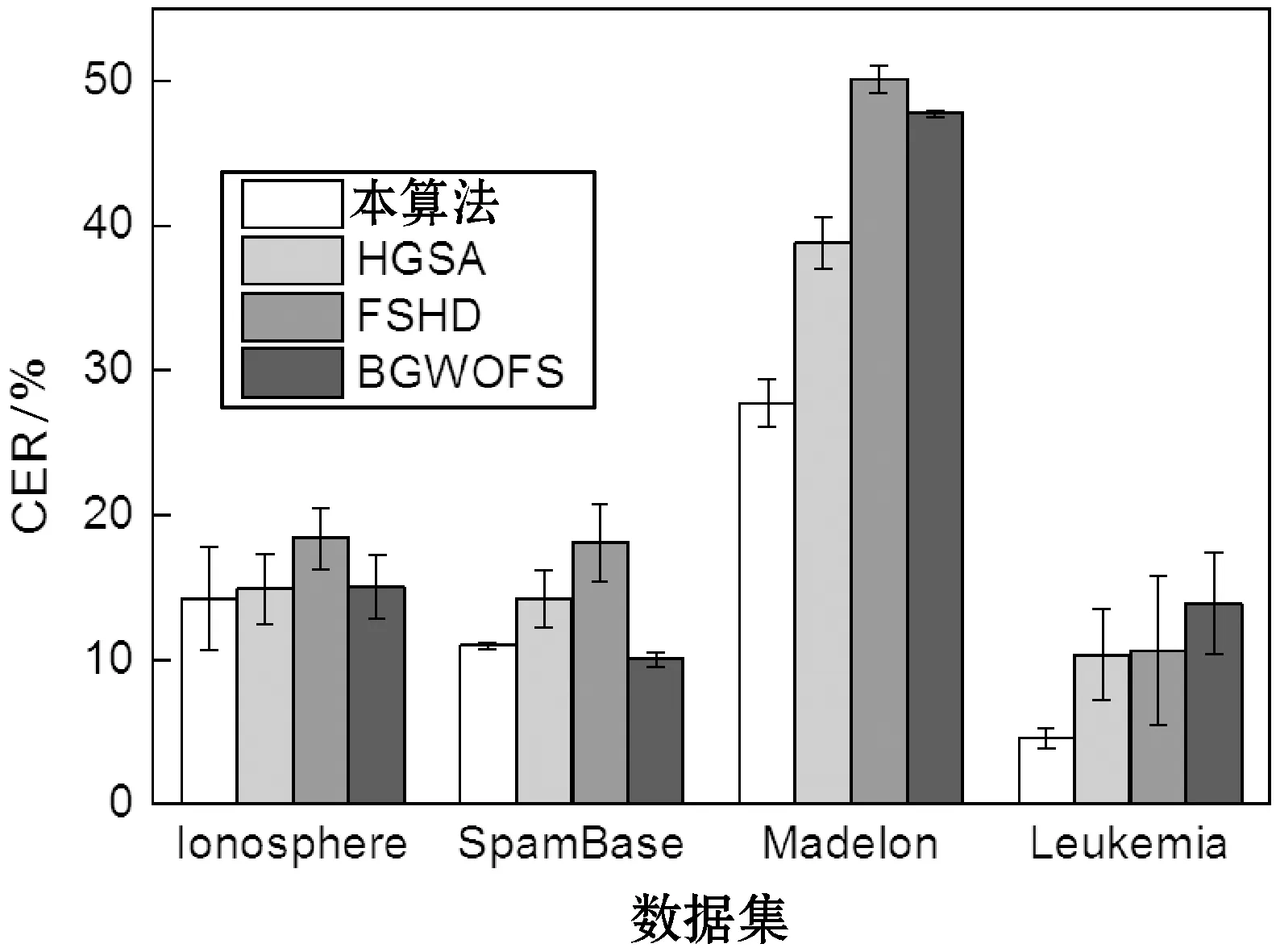
图7 RF分类器的结果

4.5 算法的时间效率

每组实验独立地重复10次，计算10次算法处理时间的平均值作为统计结果。表3是4个算法处理各个数据集的平均时间。HGSA与BGWOFS是两个基于种群的特征选择算法，这两个算法的计算时间随着特征规模的增加而剧烈增加。FSHD则是一种分布式的特征选择算法，其计算时间随着特征规模的增加呈现缓慢增长的趋势。本文算法是并行算法，即使对于大规模的特征集，本文算法也能分为若干的特征子集，并行地处理每个特征子集，而人工蚁群算法分别处理每个小规模的循环无向图，实现了合理的计算成本。

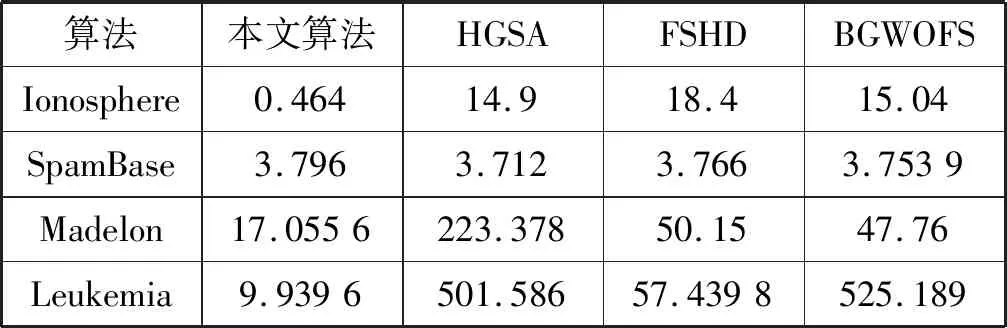
表3 4个算法处理各个数据集的平均时间 s

4.6 对高维数据集的分类器性能

上述实验评估了本算法对于低维数据集的性能，本算法的优势主要在于对高维数据集的处理效果。选择另外两个高维数据特征选择算法与本算法比较，分别为：BKHAFS[18]、TSSLR[19]。BKHAFS是一种新型的基于二元磷虾群的高维数据特征选择算法，TSSLR则是一种基于两阶段稀疏Logistic回归的高维数据特征选择算法。

图8-图11所示分别为三个高维数据特征选择算法与SVM、DT、KNN和RF四个分类器的性能结果。每组实验独立地重复10次，计算10次CER值的平均值与标准偏差作为统计结果。从图中可看出，本算法对于文本数据集与微阵列数据集的处理性能均优于其他两个算法。主要原因在于BKHAFS与TSSLR均将减少不相关特征作为目标，而忽略了冗余特征对分类性能的干扰，导致特征集中包含噪声与冗余特征，影响了分类器的分类性能。本算法则同时将减少不相关特征与减少冗余度作为目标，实现了较好的特征提取结果。

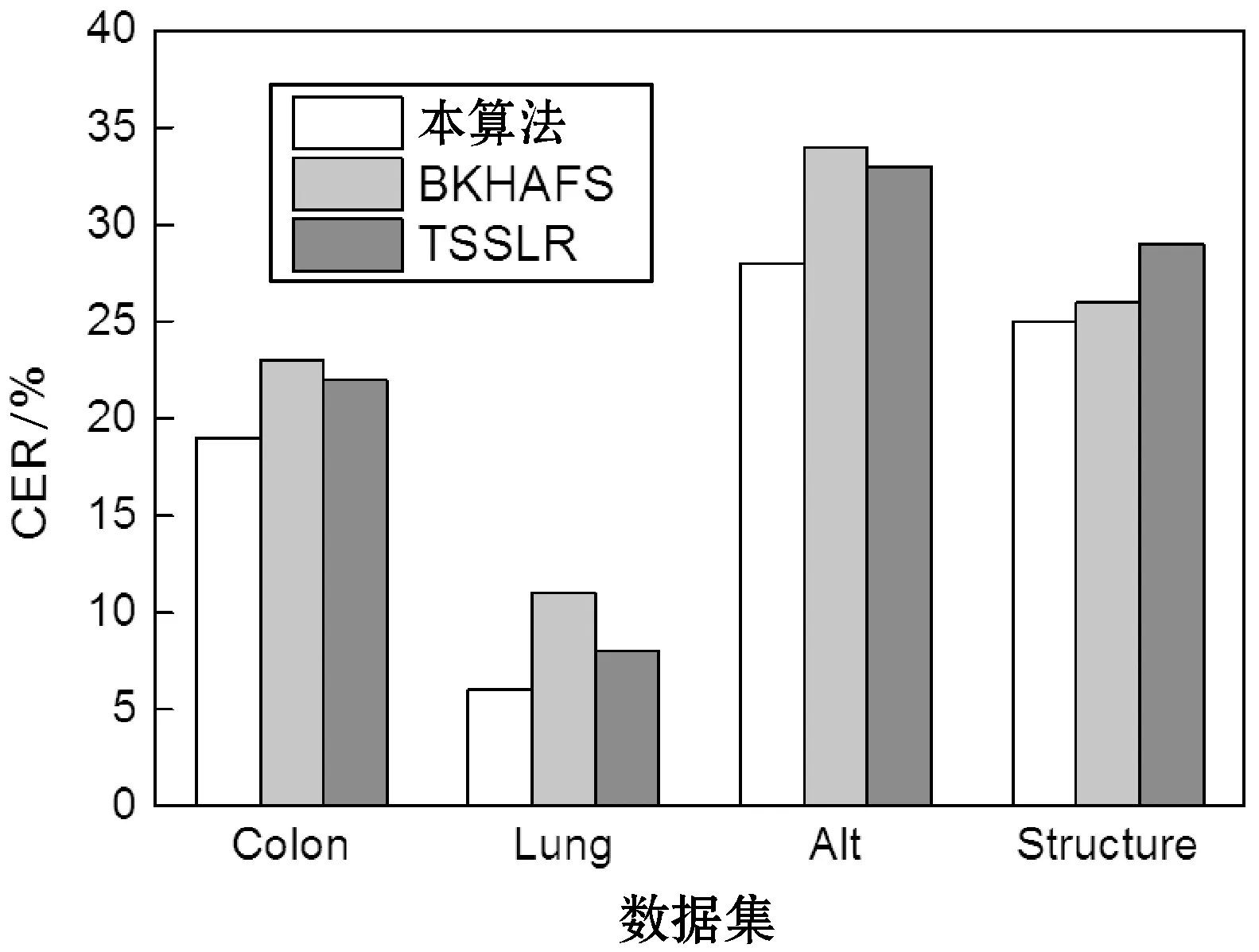
图8 SVM分类器的结果

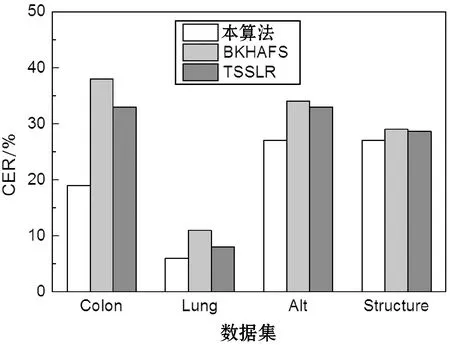
图9 NB分类器的结果

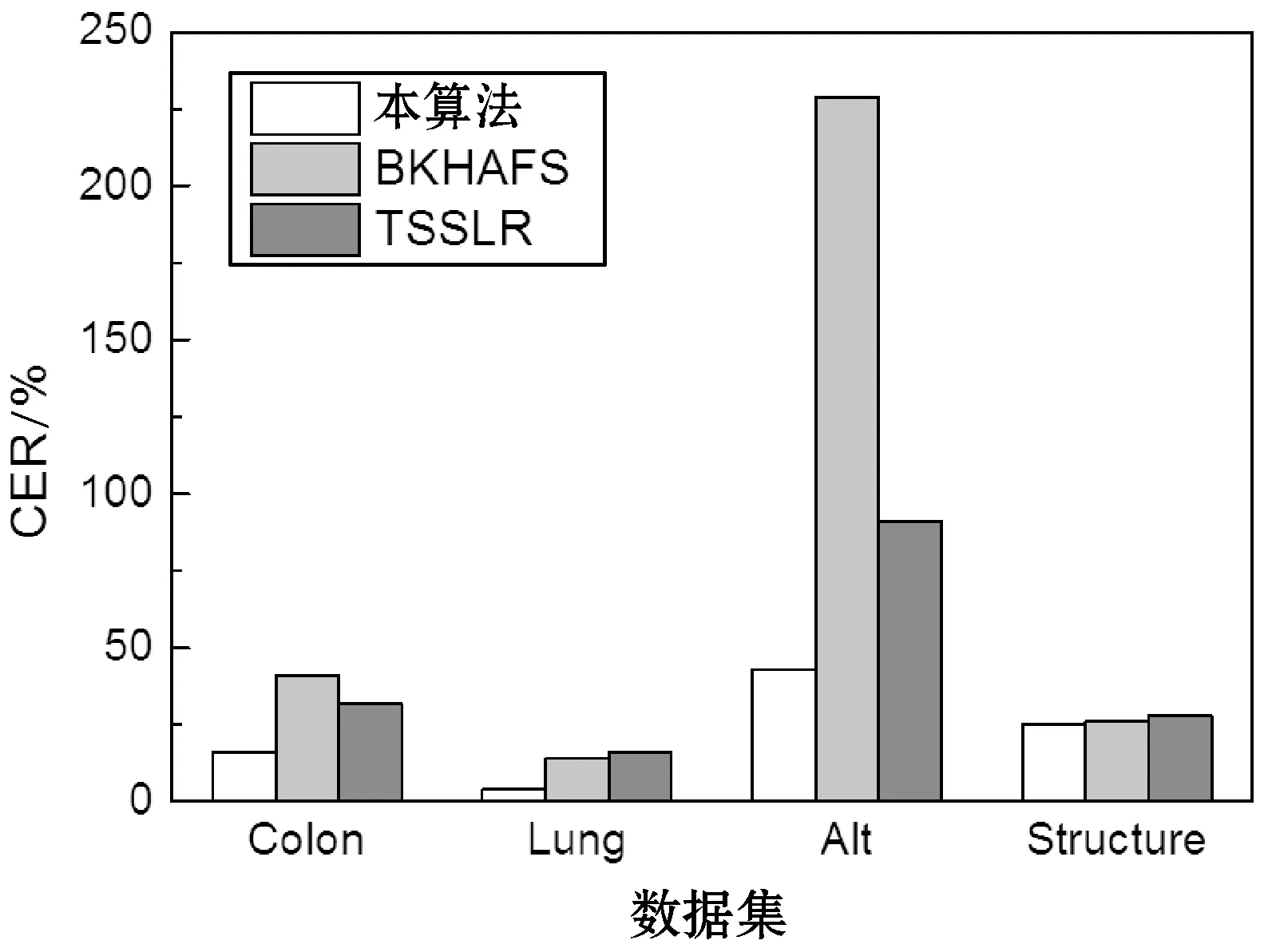
图10 DT分类器的结果

图11 RF分类器的结果

5 结 语

许多研究将减少不相关特征作为目标，而忽略了冗余特征对分类性能的干扰，本文将减少冗余特征与不相关特征作为特征选择的两个目标。人工蚁群算法的求解效果较好，但是计算成本较高，为此设计了基于社区检测的并行特征选择方法。通过加权社区检测技术将特征集分类，对每个分类分别采用EACO并行地选择特征集，然后设计了全局的竞争机制处理所有分类的最优特征，选出全局最优的特征集。本方法提高了特征选择的性能，实现了合理的计算效率。

本算法采用Pearson相关系数作为特征相似性的度量指标，未来将重点研究针对特定数据类型的相似性度量方法，从而提高特定应用问题的特征选择效果。