作文段落句间逻辑合理性等级评测

杨正祥 刘 杰* 袁克柔 周建设

1(首都师范大学信息工程学院 北京 100048)2(首都师范大学成像技术高精尖创新中心 北京 100048)

0 引 言

作文写作可以考察学生的逻辑思维与语言运用的能力和水平，是汉语考试中必考科目。国内每年学生写作的作文数目十分巨大，人工批改的成本极高。中文作文的自动评测研究逐渐兴起，对于提高作文评测效率、控制评分误差具有十分重要的意义。

由于中文语言逻辑的复杂程度高，现有的研究对作文评测大多从词汇使用[1]、语法表达、作文长度、关联词使用、修辞手法的运用[2]、文章主题一致性等角度而进行评测，并未涉及作文句间逻辑合理性的评测。而且，在作文评测中句间逻辑合理性同样是评价语言运用能力的一项重要指标。本文认为文本句间逻辑合理表现在句子组织顺序合理，这样的文本具有很好的可读性。因此，本文考虑使用句子自动排序的方法，通过判定句子集合的自动排序是否与人工排序一致，验证句间逻辑是否合理。

1 相关研究

本文以段落为基础，研究中文作文段落中句间逻辑合理性的等级判别模型。语篇连贯性的研究可以从关联词及语法信息的方面进行分析判断[3],另外根据句子组织顺序合理性也可以有效判断段落逻辑合理性。

句子排序的研究出现在文本自动摘要研究领域，其他领域并无相关研究。这是因为人工写作的摘要结构单一且内容精炼，涉及的词汇多为某领域内的专业词汇。文本自动摘要领域内的句子排序任务，主要是将人工已写好的、打乱顺序的文档摘要句集或机器选择的摘要候选句集组织为合理并且可读的文摘[4]。无论是单文档还是多文档自动摘要，都不可避免地要面临以下三个问题：文档冗余信息的识别与处理，重要信息的辨认，生成文摘的连贯性[5-9]。其中，文摘的连贯性与本文所要研究的段落内部句子之间的连贯性是非常有关联的，因此本文借鉴文本自动摘要中关于连贯性的处理方法，将其迁移应用到中小学作文的段落句间连贯性的研究上。

现有的研究大致可分为以下几类：① 利用句中时间信息确定句子顺序。以句子在语料中出现的时间为依据进行排序，例如新闻语料中，抽取句子内部的时间信息，再辅助排序算法对句子进行排序[10-11]。② 从大型的语料中挖掘内部句子的自然顺序。该方法在语料词汇的基础上，计算相邻句子间的邻近度，估计句子构成前后句对的条件概率，得到排序结果[12-14]。③ 从文档集合中句间的蕴含关系确定逻辑关系。该方法从句子内部实体在句间的转移、事件标签的延续状态、主题转移等方面挖掘句间所蕴含的逻辑关系[14]。文献[16]采用注意力机制的方法捕捉句子间的语义逻辑关系。

利用句子所包含的顺序信息、句间的继承关系、句子主题等方法，局限性较大，且对时间词以及隐含的时间的识别、主题识别、显示及隐式关联词挖掘等成为需要克服的技术难题。

考虑到现有语料数量巨大，人工标记不足，本文拟采用非监督方法，在不依赖时间、事件等标签，保证方法通用的前提下，挖掘段落内部句间的逻辑关系，获得较优的通用性。该方法在现有条件熵计算相邻句子间关系的基础上，提出词向量以及哈工大同义词词林(cilin)与其结合的方法，共同计算句子的邻近度；在排序算法上，则选取马尔科夫随机游走模型[17]，完成中小学作文段落内部的句子排序任务，并通过ROUGE-L[18]对排序结果打分，从而实现对段落逻辑合理性的等级评测，构建段落逻辑合理性等级评测模型(Logic Rationality Rating of Paragraph Model, RPM)。

2 段落句间逻辑合理性等级评测

中文作文句间合理性评测模型以条件熵为基础来计算句对关联程度，融合word2vec以及哈工大同义词词林，从语义相似的角度计算句子的邻近度，再依据马尔科夫随机游走模型，完成中小学作文的句子排序。为了评价排序结果与真实排序是否一致，选择使用ROUGE-L作为评价指标，模型排序结果与待评语料的真实排序顺序比较，若评价指标值大于等于0.6，则认为模型排序结果较接近语料的真实排序，排序是一致且可接受的，否则排序结果不可接受。通过在测试集上统计经模型得到的可接受排序比例，验证文中提出的句子排序方法是否能与真实排序一致，从而辅助评测作文句间逻辑是否合理。具体模型如图2 所示。

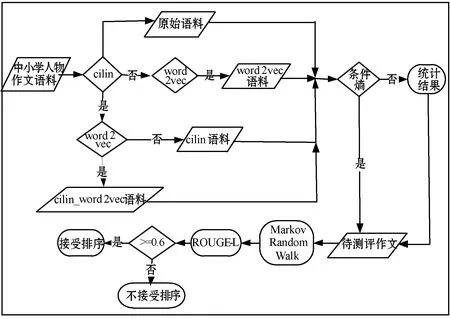
图1 段落逻辑合理性等级评测模型

2.1 条件熵算法

信息熵描述信源的不确定度，信息越有序熵越低，而信息越混乱熵较高，包含的不确定信息更多。从句子排序的角度来说，两个句子之间的连接越紧密，关联程度越强，而熵值就越小，依此为依据，依靠条件熵衡量不同句子间的连贯性强度。在本文中，条件熵作为评价两个变量，即两个句子之间信息关联程度的评价基础，其计算公式如下：

(1)

式中：X、Y是两个变量的集合，xi∈X，yj∈Y，p(xiyj)是xi、yj共同出现的概率，p(yj|xi)是条件概率，表示在xi出现的情况下，yj出现的概率。

在句子排序的研究中，句子作为单独的语义单元，出现相同表达的可能性几乎为零，词作为构成句子语义的最小单元，可重复出现在不同的句子中。因此，本文选择以句对间的单词搭配信息，来计算句间连贯性，对应的计算公式如下：

(2)

式中：Sm与Sm-1为相邻的两句话，wi为Sm-1中出现的词，wj为Sm中出现的词。考虑到语料词性中名词、动词、形容词在中文中表达意义比较丰富，因此在研究过程中，同样仅考虑了以上三种词性。p(wiwj)以及p(wj|wi)均可从语料中统计得出，计算公式如下：

(3)

(4)

式中：wi为前导句中出现的单词，wx为其后面句子中出现的单词，frequency(wxwy)计算两个单词共同出现的频次，frequency(wywi)计算wi与其他任意词搭配的频次。

2.2 word2vec以及同义词词林

由于统计语料中句对之间的词语搭配，参数空间大，且容易出现数据稀疏的问题，本文将借助语义词典，如词向量、《哈工大信息检索研究室同义词词林扩展版》，在语义上对词语进行划分与聚类，以降低不良影响[19]。

Google在2013年开源了一款用于词向量计算的工具word2vec[20], 该工具能够在上亿的数据集上进行高效训练，并且得到词向量可以度量词与词的相似度。本文根据十万篇不同类型的中小学作文语料，得到词向量字典，并将其按照相似程度聚类，每类下的单词可以认为其语义是相似的。

梅家驹等编辑完成的《同义词词林》为创作和翻译工作提供了较多的同义词语。《同义词词林》著作时间为1983年，较为久远，内容对当今所处的时代差距较远，因此《哈工大信息检索研究室同义词词林扩展版》应运而生，其中包含了更加丰富和符合当代背景的语义信息。但是能够共享的仅仅是其中的词典文件，其完整版并没有共享。词典内容的缺失必然会导致作文中未出现在词林中的不相干词汇划分为同一类别。因此，本文在同义词林(cilin)的基础上，加入word2vec对词典文件缺失的词汇进行近义词、同义词自动聚类，以降低因cilin内容缺失而带来的不良影响。

2.3 马尔科夫游走模型

在确定句间的邻近关系后，本文在众多排序算法中，选择马尔科夫随机游走模型(Markov Random Walk)对句子进行最终排序。随机游走(Random Walk)矩阵对应一个遍历的马尔科夫链，任意两个状态之间通过不断转移可以互相到达。如图2所示，每个状态节点之间可以以一定的概率p连接转移。

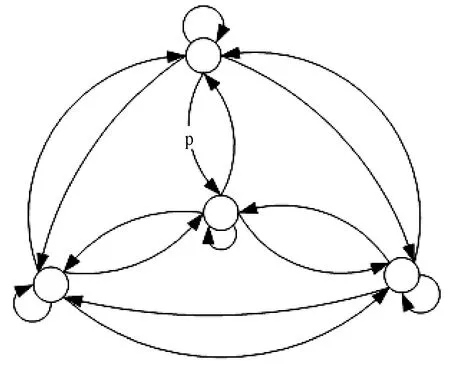
图2 马尔科夫随机游走模型

排序模型定义了图G=(V,E)，V是顶点集，即待排序句子集合，E是边集，即待排序句子集合中两个句子的邻近度，其值即为通过条件熵公式计算得到的句子vi→vj的概率。m个待排序句子可得到游走矩阵模型M=Mi,j|m×m，其中：

(5)

基于矩阵模型M，某个句子在排序中的分值可通过与其他句子得到，其计算公式如下：

(6)

图G=(V,E) 按照以上计算直至收敛，选取其中分值最高的句子优先排序，将剩余句子重新组成新图G′ 重新执行操作，直至待排序句子V为空。句子的排序顺序即为最终的排序结果。

2.4 评估算法与标准

因为本文所使用的语料数据量较大，人工评价模型不适合评估排序结果的合理性。因此，考虑自动的句间合理性评测方法，由于自动文摘的连贯性与作文段落句间连贯性评估标准非常相似，在自动文摘中使用ROUGE系统对自动生成的摘要与参考摘要进行比较计算得到相应分值，通过衡量二者相似度来分析文摘的连贯性。在本文中考虑模型排序结果与真实排序结果的相似度来分析段落句间的连贯性，所以采用ROUGE系统进行句间逻辑合理性评估。ROUGE系统中的ROUGE-L从两个序列的最长公共子串的角度考虑，进行相似度的打分。计算公式如下：

LSC=lsc(stand_order,sorted_order)

(7)

(8)

(9)

(10)

(11)

式中：stand_order是段落中句子集合真实的排序结果，sorted_order是排序模型生成的结果，LSC为两个排序的最长公共子串的长度，R、P分别指的是召回率和准确率，标准排序和模型排序结果的长度是一致的，公式经过化简，最终ROUGE-L的评分由公共子串在序列长度中的比例决定。本文通过实验将阈值设置为0.6，真实排序序列同模型排序序列比较，若评价分数大于或等于阈值，则两者排序结果是相似的，将模型排序的排序结果是可接受的，否则不接受模型排序。

3 实验结果与分析

3.1 数据集

本文从互联网上优秀的作文网站中使用爬虫工具获取中小学汉语作文语料16 329篇，其中，训练数据11 766篇，测试数据为4 563篇。并且将上述所有作文语料作为word2vec的训练语料，获得最终的词向量字典，共计79 770个词。

3.2 条件熵与词向量、cilin效果对比

本文使用条件熵预测句子排序结果。由于句中语义信息缺失，本文在此基础上，提出的应用word2vec，从数据集中训练得到的词向量字典，将所有单词聚类为500类与1 500类效果较优。此外，考虑到单词自动聚类不如人工聚类准确，本文考虑并加入了《哈工大信息检索研究室同义词词林扩展版》涉及的11 769类同义词，融合基础模型条件熵，通过马尔科夫随机游走模型预测句子排序。实验结果如图3 所示。

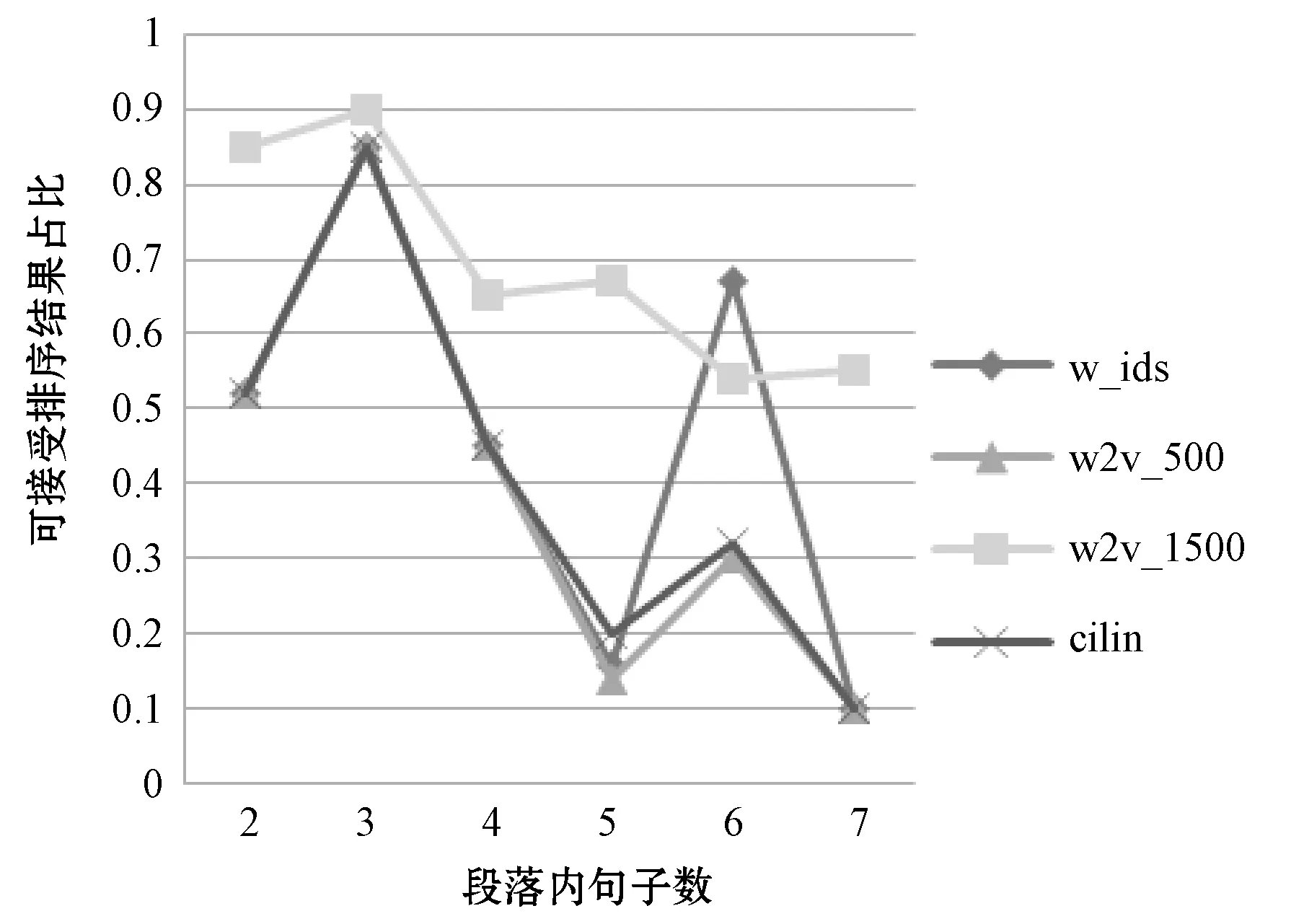
图3 ROUGE-L评测结果

由实验结果可知，针对句子数量相同的段落：采用原始词语的字典编号取得的效果很差；词向量能够优化条件熵的排序结果，且单词分类越多，各个类别下单词的语义相似，模型排序与原始排序通过ROUGE评分，可接受部分越多，最高能达89%左右，且实验中无论段落内部句子的数量，通过评价，可接受比例均在50%以上；cilin的使用能够在一定程度上优化排序结果，虽然效果优于采用聚类为500类的词向量模型，但远远不如将单词聚为1 500类的模型。然而，随着段落内句子数量的增多，模型越难以对段落的逻辑做出合理排序。

3.3 cilin、词向量融合效果对比

在上述实验中，cilin与word2vec聚类均能提升条件熵的排序效果，且word2vec聚类1 500类之后取得了最优的效果，远远高于应用cilin的模型。本部分将cilin与word2vec聚类1 500类的方法融合，在此基础上加入条件熵，通过马尔科夫随机游走模型预测句子排序。结果如图4所示。

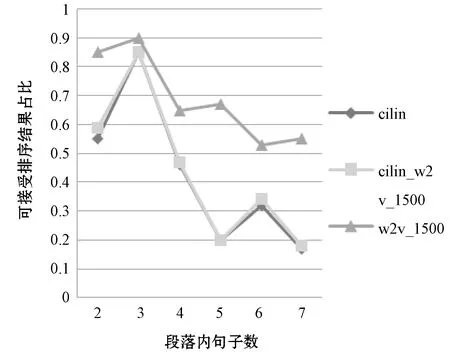
图4 ROUGE-L评测结果

由实验结果可知，cilin与word2vec聚类相结合的方式与单独cilin模型排序的效果相比，总体上稍有提升。但是仍不及单独用word2vec聚类1 500类的模型排序效果。分析其具体原因，word2vec用高维特征表示单词语义，词向量不仅能够包含单词的语义，还包含更多诸如语法结构等方面的信息，对其表征的词语进行聚类，相比cilin中词语仅依靠相近的语义聚类在一起，前者能从多角度多维度考虑词语的类别，更为合理。而两者融合，cilin对w2v_1500造成了不良影响，由ROUGE评分后，排序结果的可接受比例出现了明显下降；w2v_1500则一定程度上弥补了cilin不完整的缺陷，排序结果可接受比例稍有提高。

3.4 评测结果分析

从实验结果可知，随着段落长度的增加，模型排序结果经ROUGE系统评分，可接受的排序在所有排序中的比例越来越低，这主要是由模型算法自身缺陷导致的。RPM模型在对句子数量为2或3的段落排序，可接受的排序结果占的比例较高，取得了不错的效果，但是即使假设2句话的排序可接受占比达到0.9，随着句子数量越来越多， 在段落内句子数量为n的情况下，可接受的排序结果占比最高仅能达到0.9n，呈指数级别下降。

4 评测模型的优化

4.1 带优化策略的段落逻辑合理性评测模型

即使算法能够具有一定的通用性，在句子数量较少的段落情况下，RPM模型排序结果取得了不错的效果，但是随着段落内部句子数量的增多，排序结果的可接受比例指数下降，在实际评测中存在缺陷，因此本节对以上提出的条件熵模型进行改进。

经实验分析可知，段落内句子数量为2或3的情况下，RPM模型排序的结果比较令人满意。因此，本节拟通过对句子数量较多的段落首先进行拆分分块，以保证RPM模型仅处理句子数量为2或3的句子块。若段落内句子数量较多，段落可以被认为是包含很多叶子(段落内的句子)的树，段落整体作文根节点，对段落的每次划分，相当于对子节点的生成。在保证RPM仅处理句子数量为2或3的句子块的前提下，每个节点下的子节点数量应在2～3范围内。但是，本文实验仅考虑了句子数量为2～7的段落，可以通过简单的拆分表，对段落进行划分。表1为拆分表，图5展示了拆分过程。

表1 段落拆分表

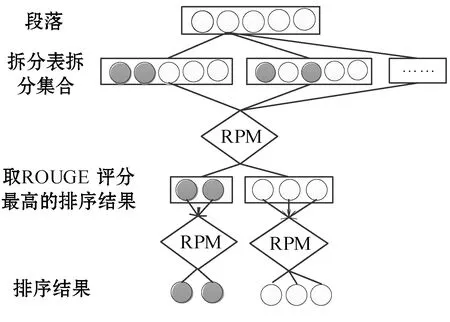
图5 拆分排序过程

图5 展示了句子数量为5的段落的拆分排序过程。首先对段落内句子按照拆分表进行分块划分，每种不同的拆分情况内，每块段落片段代表不同的类别，将相同块内的句子当作一个整体，从而能够应用RPM模型进行评分，完成块之间的排序。之后比较每种拆分的取得的ROUGE分值，取最高得分的块排序结果作为第一次的排序。然后每块内部再进行拆分或排序，同样取分值最高的排序结果作为当前排序结果。如此层次拆分，最终得到段落句子的最终排序。

4.2 优化策略模型实验结果

分析上一节中的实验结果，RPM融入经词向量聚类1 500类的语义相似词，在段落内句子数量为2～3的情况下，取得了不错的效果。本次实验以此为基础，建立OPT_RPM评测模型，验证优化策略的可行性。

由图6可以看出，优化策略能够减缓RPM随着段落内句子数量增多而存在的可接受排序结果占比指数下降的情况，对长度为4～5的段落句子排序结果的可接受比例有了较大的提高，从而验证本文提出的带优化策略的RPM，即OPT_RPM是可行的。

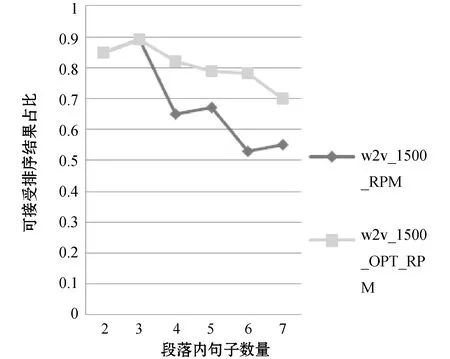
图6 OPT_RPM的ROUGE-L评测结果

5 逻辑等级与ROUGE分值对应关系

本文扩展可接受与不可接受两种评测结果，拟将段落的逻辑划分为4个等级：优秀、良好、及格以及不及格。为了能够在实践中应用，本节通过一系列的统计分析建立段落逻辑等级与ROUGE分值的对应关系。

本文选取1 000条段落，每个等级的段落均为250条，其评判等级均有专家参与，保证语料的准确性。使用OPT_RPM对句集排序得到机器排序结果，ROUGE-L对其进行评分。通过分析每个逻辑等级内ROUGE分数的范围，从而确定模型在实际应用中所使用的阈值。

OPT_RPM对每条段落进行句子排序，而ROUGE-L对排序结果进行了评分，本文将评分与人工真实评价等级对应起来，除去离散点，取分布最集中的分值作为ROUGE-L对段落逻辑等级划分的边界。其中，相邻等级之间存在交叉，本文考虑到划分边界模糊，为了激励使用者，将交叉冲突部分取等级较高的一方，最终得到表2 关于段落逻辑等级对应的ROUGE-L分值区域。由该表可知，1 000条段落通过ROUGE-L评分，判断分值散落在的区间对应得到段落评测等级，各个等级的评测准确率均在72%以上。

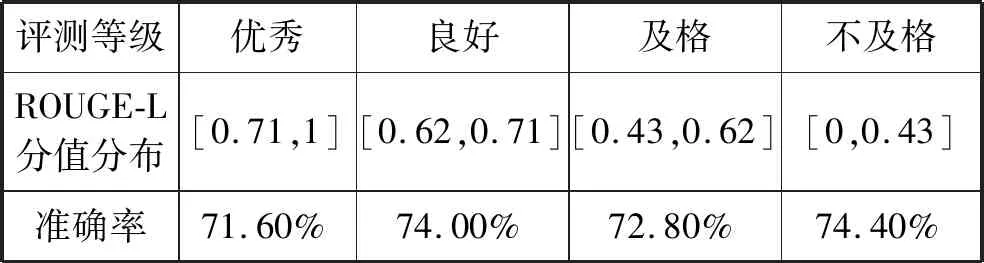
表2 段落逻辑等级与ROUGE-L评分对应关系

6 结 语

本文从句子排序角度提出评测句间逻辑合理性，对其进行定量分析。通过判定句子集合的排序与人工排序的相近程度，验证排序模型的有效性。在研究的排序方法中，应用word2vec、cilin以及两者相结合的条件熵句子排序方法均优于仅仅使用条件熵进行排序的方法。其中，词向量词典用高维特征表示单词语义，不仅能够包含单词的语义，还包含更多诸如语法结构等方面的信息，对其表征的词语进行聚类，相比cilin中词语仅依靠相近的语义聚类在一起，前者能从多角度多维度考虑词语的类别，在聚类为1 500类时，表现最佳；另外，本文提出了带优化的句间逻辑合理性评测模型OPT_RPM，经过实验证明，OPT_RPM对相同的实验数据进行了排序，由同一评测标准评测，取得了最优的效果；本文还对OPT_RPM在实际中的使用做了探究工作，通过统计分析了OPT_RPM对段落排序结果的ROUGE-L分值与由专家评判的段落逻辑合理性等级的对应关系，确定了ROUGE-L与逻辑合理性等级判定的分类边界，取得了不错的效果，为辅助中文作文智能评测提供了新思路。在未来的研究工作中，将计划进一步优化条件熵算法以及马尔科夫游走模型，从模型结构上改进提高算法评测效果,探索更多评估作文段落逻辑合理性的方法，努力推进中文作文智能评测研究的发展。