基于FPGA的变M/T归一化测速算法研究

李小闯 于 强

1(中国科学院国家空间科学中心 北京 100190)2(中国科学院大学 北京 100049)

0 引 言

在我国空间材料科学实验的研究中，传动结构往往基于步进电机进行；步进电机虽然控制方式较为简单，但往往难以获得较大的转矩，而随着实验样品体积的增大，步进电机逐渐难以满足实验需求。而永磁同步电机虽然控制较为复杂，但因其良好的转矩特性使其拥有更好的应用前景。在空间材料科学实验中，对样品的移动速度及准确定位要求十分严格，这也对永磁同步电机的速度控制提出了较高的要求。传统的M/T测速法虽然能够有效地对电机转速进行测量，但其在低速范围的实时性较差。而在空间材料科学实验中样品的移动速度跨度范围较大(5 mm/天～2 mm/min)，因此对M/T测速算法的改进势在必行。

本文针对永磁同步电机的测速问题，结合FPGA特性，提出一种基于FPGA的变M/T的归一化测速算法，从而在保持传统M/T测速精度的同时，改善测速的实时性。同时归一化的设计思路能够使得系统能够适用于任何基于增量编码器的永磁同步电机测速环境。针对设计中所需要的乘除运算，引入Booth算法以降低设计对DSP的需求。

1 增量编码器工作原理

永磁同步电机转速测量依靠在转子上安装的增量编码器进行速度检测。增量编码器采用光电转换原理，输出两相正交脉冲信号A、B与一路零相信号Z：A、B两相相差90°，若A相超前B相，则电机处于正转,否则处于反转；电机旋转一圈零相信号Z输出一个脉冲。增量编码器输出时序如图1所示[1]。

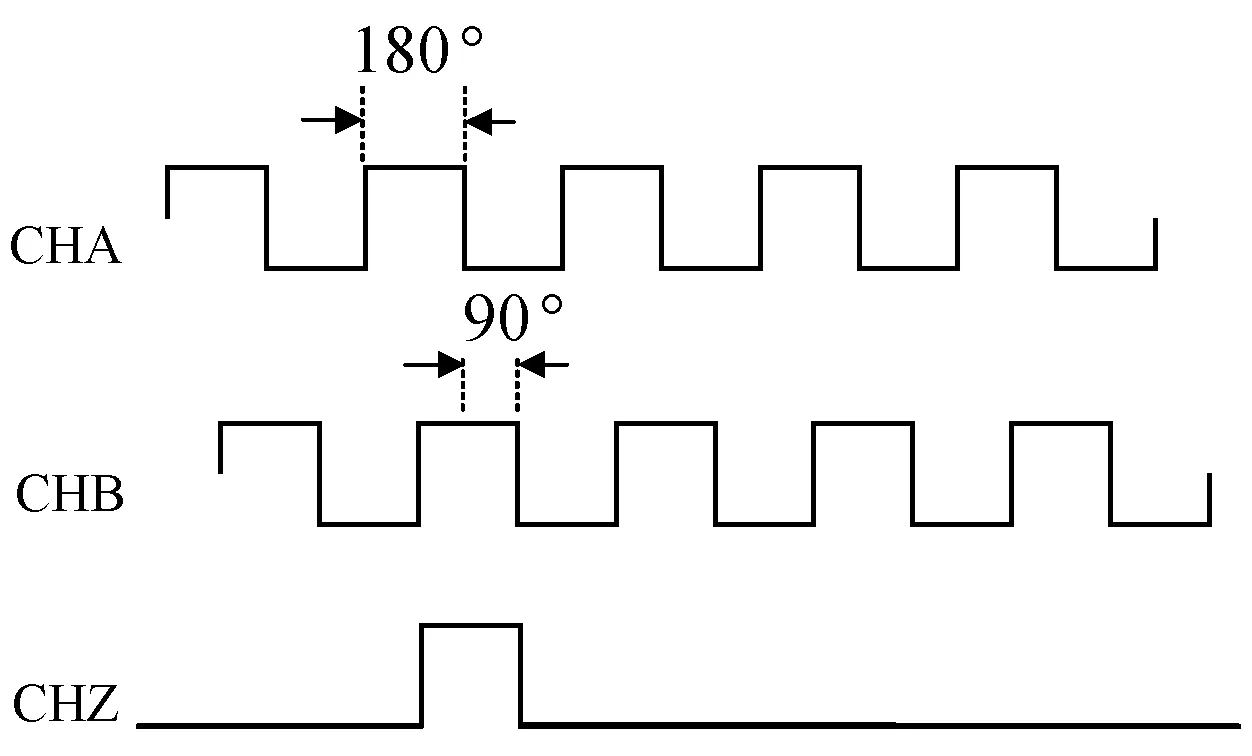
图1 增量编码器时序图

2 测速算法原理

2.1 M/T测速算法原理

M/T法测速原理是M法(频率法)和T法(周期法)的结合，其方式为在一定时间范围内，同时对光电编码器输出脉冲个数M1和捕获时钟的个数M2进行计数，用M2计算出的时间替代定时器的时间进行转速的计算[1]。其测速原理如图2所示。

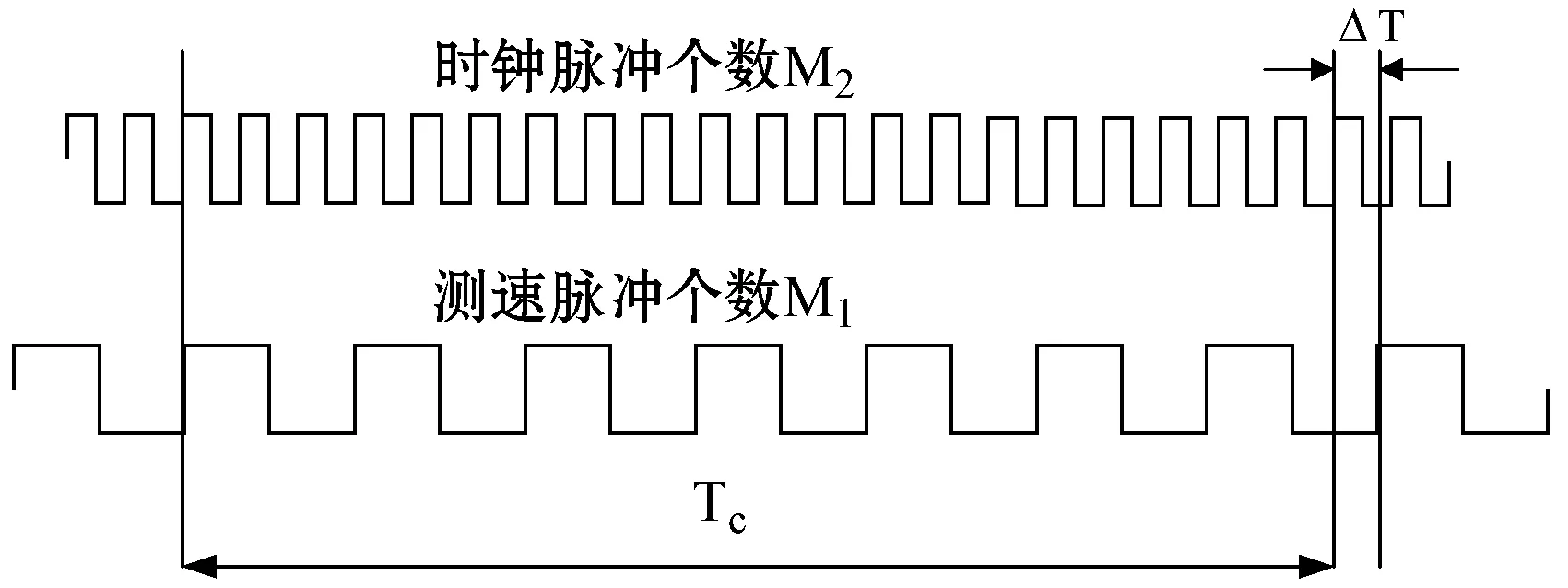
图2 M/T测速算法测速原理

假设时钟脉冲频率为fclk,编码器分辨率为N，M1为时间Tc内编码器脉冲计数,M2为时间Tc内高频时钟周期计数,则转子的转速v(单位：r/min)可表示为：

(1)

在进行计数过程中，由于检测时钟脉冲计数可能出现±1个脉冲误差[2]，因此M/T法测得电机转速误差Δv为：

(2)

相对误差为：

(3)

2.2 归一化

归一化也称标幺化。归一值(标幺值)是电力系统分析和工程计算中常用的数值标记方法，表示各物理量及参数的相对值，单位为pu(也可以认为其为无量纲)[3]。归一化是相对于某一基准值而言的。同一有名值，选取基准不同，其归一值也不同，其关系如下：

(4)

在伺服电机控制系统中，由于各种变量单位及范围不同，在采用浮点类型数据进行表示时计算性能较差，同时耗时较长，也不便于算法的移植。在FPGA、DSP等设备中，往往采用定点数进行数据的计算，这也就意味着采用实际值参与算法运算的不可行性[4]。因而归一化的引入有助于算法的定点化实现，同时也便于算法移植，减少计算周期。以Q15格式(1位符号位，15位小数位)为例，变量定点化计算方式为：

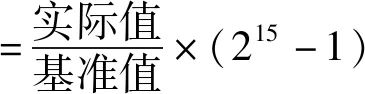
(5)

基准值的选取往往采用变量的额定值。经过归一化处理，变量取值范围被约束在[-1,+1]区间之间，各变量运算过程中不存在取值范围不同的问题。

2.3 变M/T归一化测速算法原理

M/T算法方法是统计一段时间内编码器脉冲计数与高频时钟计数来完成测速；为了兼顾算法在低速和高速时测量的可用性，其选取的统计时间往往较大，以确保无论在高速还是低速情况下测速时间窗口内均有足够的编码器计数脉冲。正是由于这一点导致M/T算法在低速模式下实时性较差的不足。

结合M/T算法测速原理，当伺服电机运转在低速模式下，为提高速度测量实时性，可采用缩短采样时间的方法。假设电机转速为v，增量编码器分辨率为N，则增量编码器单个脉冲周期时长t(单位：s)为：

(6)

可见，增量编码器单个脉冲周期与电机转速成反比。在低速情况下，可通过减少统计的编码器脉冲个数来减少算法响应时间。由此在系统运行过程中可通过实时监测编码器脉冲时长来动态调节测速时间以加快系统响应。

假定转速测量周期为T，则在测量周期内通过的增量编码器脉冲数M1为：

(7)

可见，M1与转速v成正比。通过针对不同转速范围设定不同的M1值可使得伺服电机无论高速运行还是低速运行均能有较高的测量精度以及较短的响应时间。同时对伺服电机转速测量归一化[5]，式(1)将变为：

(8)

式中：vrated为伺服电机的额定转速，该处采用Q15数据格式。

变M/T归一化测速算法能够在保证测量精度的同时，有效改善传统M/T测量算法低速实时性较差问题，对速度的变化将更敏感，同时归一化设计思路有利于定点化实现及算法移植。

2.4 Booth算法

在FPGA程序设计实现中，对于运算中的乘除法操作往往基于片内DSP运算单元进行。对于卫星上设备而言，其所选用芯片型号往往资源受限较多，Booth算法[6]能够有效降低算法对片上DSP单元的依赖。

Booth算法采用相加减的操作计算补码数据的乘积，其对乘数从最低位开始判断，根据后两个数据位的情况进行加法、减法或仅仅进行移位操作。判断的两个数据位为当前位及其右边的位(初始时需要增加一个辅助位0)，移位操作是向右移动。假定被乘数A及乘数B位宽为N，算法实现思路为：

(1) 乘数B“负一位”补零，乘积项P(2N+1位宽)寄存器清零；

(2) 乘数B填入P低N+1位；

(3) 按照表1对乘积项P低两位进行判定，根据判定结果对乘积项P高N位进行+A、-A或无操作，无视符号位溢出；

表1 Booth算法累加规则

(4) 判定乘积项P最高位，若为0则P右移高位补零，反之右移一位补1；

(5) 重复步骤(2)-步骤(4)N次；

(6) 乘积项P前2N位即为乘积项计算结果。

Booth算法能够有效利用FPGA的移位特性、简化乘法计算步骤、对于N位乘法计算其仅需N个时钟周期。

同时针对式(8)中的常量乘数项借鉴Booth算法编码规则可修改为：

(9)

通过将常量乘法转换为移位操作能够进一步降低对乘法器的依赖。

3 算法实现

为加快系统响应，算法设计基于FPGA平台进行实现。FPGA基于LUT+FF的结构使得算法能够高度并行化[7]。变M/T归一化测速算法分为预处理模块、速度区间预测模块及速度测量模块。其设计框图如图3所示。

图3 变M/T归一化测速算法设计框图

3.1 预处理模块

预处理模块包括信号同步、正交编码、方向预测三部分功能。

在FPGA设计中，对于外部多比特信号的采样牵涉到多比特信号跨时钟域处理从而避免亚稳态情况。但正如图1所示，增量编码器A、B两相信号相差90°，在同一时间只有一个比特位发生信号跳转，类似于格林编码，故而信号同步逻辑可通过单比特信号跨时钟域处理方式进行信号的同步。相比于多比特信号跨时钟域处理，单比特信号跨时钟域处理采用寄存器打拍形式即可，资源消耗较少[8]。

增量编码器A、B两相信号在一个脉冲周期内分别有两个状态、通过正交编码的处理，可形成四个状态。在此处设计中采用“异或”逻辑对两相信号处理，可获得更高的分辨率。而方向预测单元通过A、B两相相位关系获得电机转速方向。

3.2 速度区间预测模块

速度区间预测模块包括脉冲计时单元、超时保护单元及速度预测单元。

由式(6)可知，增量编码器单个输出脉冲周期与转子转速成反比，据此可由编码器单个脉冲周期来预判电机转速区间范围。

脉冲计时单元基于系统时钟对由正交编码输出信号单个脉冲信号进行计时，获取单个脉冲时间，同时在超时保护单元中设置计数阈值以避免在超低速情况下脉冲计时单元长时间无有效输出的情况。

速度预测单元根据编码器单个脉冲时长决定M/T测速法脉冲计数M1值，为节省资源开销及较少计算量，可根据脉冲时长区间指定不同的M1值，而不必按照式(7)的线性关系确定。

3.3 速度测量模块

速度测量模块包括脉冲计数单元、时钟计时单元、转速计算单元及归一化单元。

速度测量模块每完成一次速度测量则从速度区间预测模块获取脉冲计数值M1作为下次速度检测时脉冲计数。脉冲计数单元则完成正交编码单元脉冲计数，并由时钟计时单元基于系统时钟统计M1个编码脉冲所占用的时钟节拍M2。

转速计算单元与归一化单元完成伺服电机转速的计算及归一化。系统运行之前首先获取电机的额定转速值，通过式(7)完成电机的转速归一化化测量。

4 仿真结果与分析

实验设计采用Xilinx A7系列芯片作为系统主控芯片，基于VIVADO完成算法的实现及仿真[9]。算法设计资源占用情况及部分仿真图如图4、图5所示。系统时钟频率50 MHz，编码器分辨率为2 048线，电机额定转速4 500 r/min。

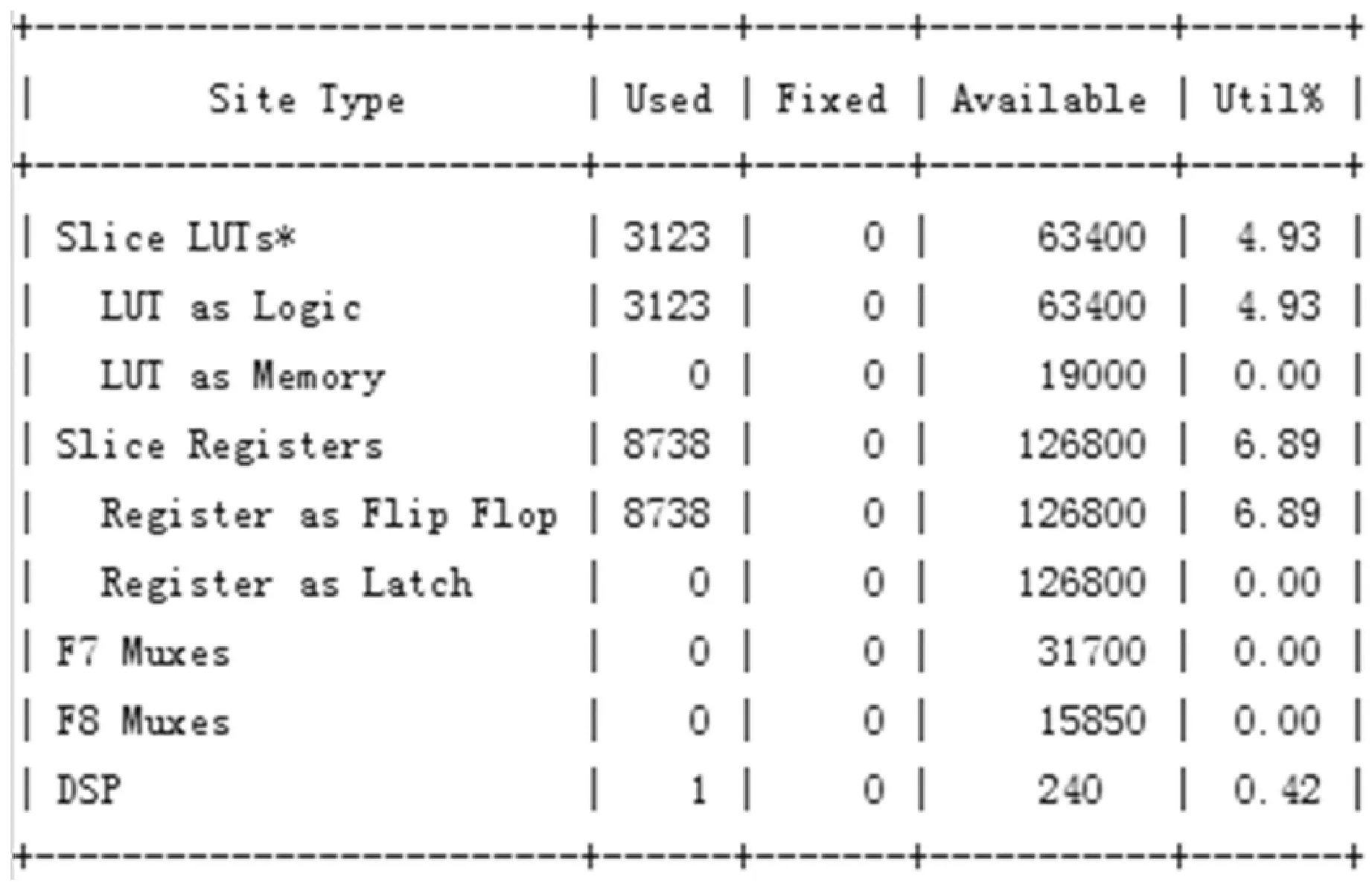
图4 资源利用报告

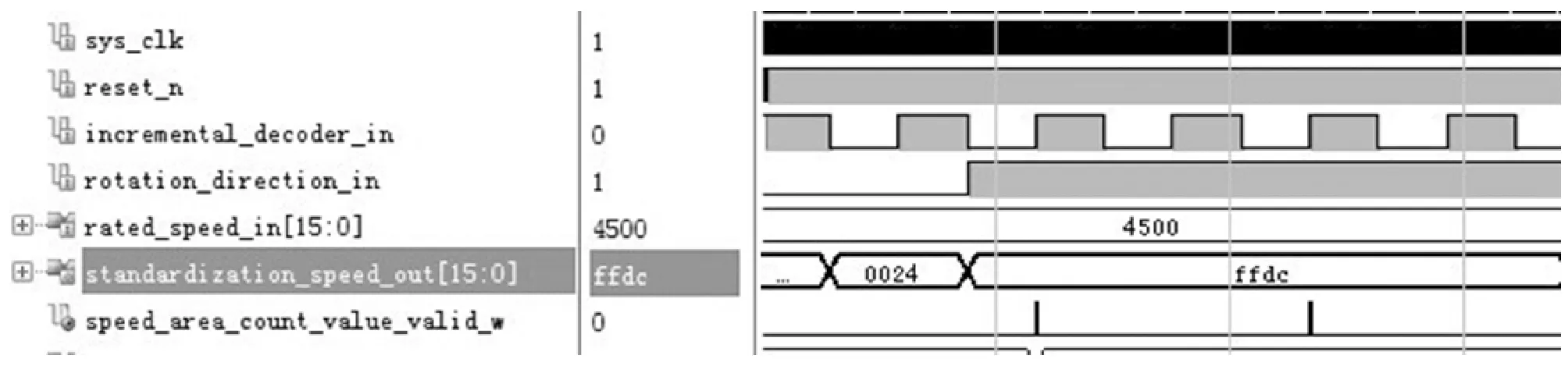
图5 算法仿真波形

从资源利用报告上看，整体设计上仅消耗2 260 LUT、5 609 FF及一个DSP运算单元用于除法操作，相对于整体片上资源而言只占用了非常小的一部分，而Booth算法的引入也极大降低了算法对DSP的依赖性。图5显示了当测量转速为+5 r/min、-5 r/min时的标幺化输出结果分别为0x24、0xffdc，与相应转速理论归一值一致。

针对不同转速输入，实验仿真结果及其绝对误差分别如表2、图6所示。

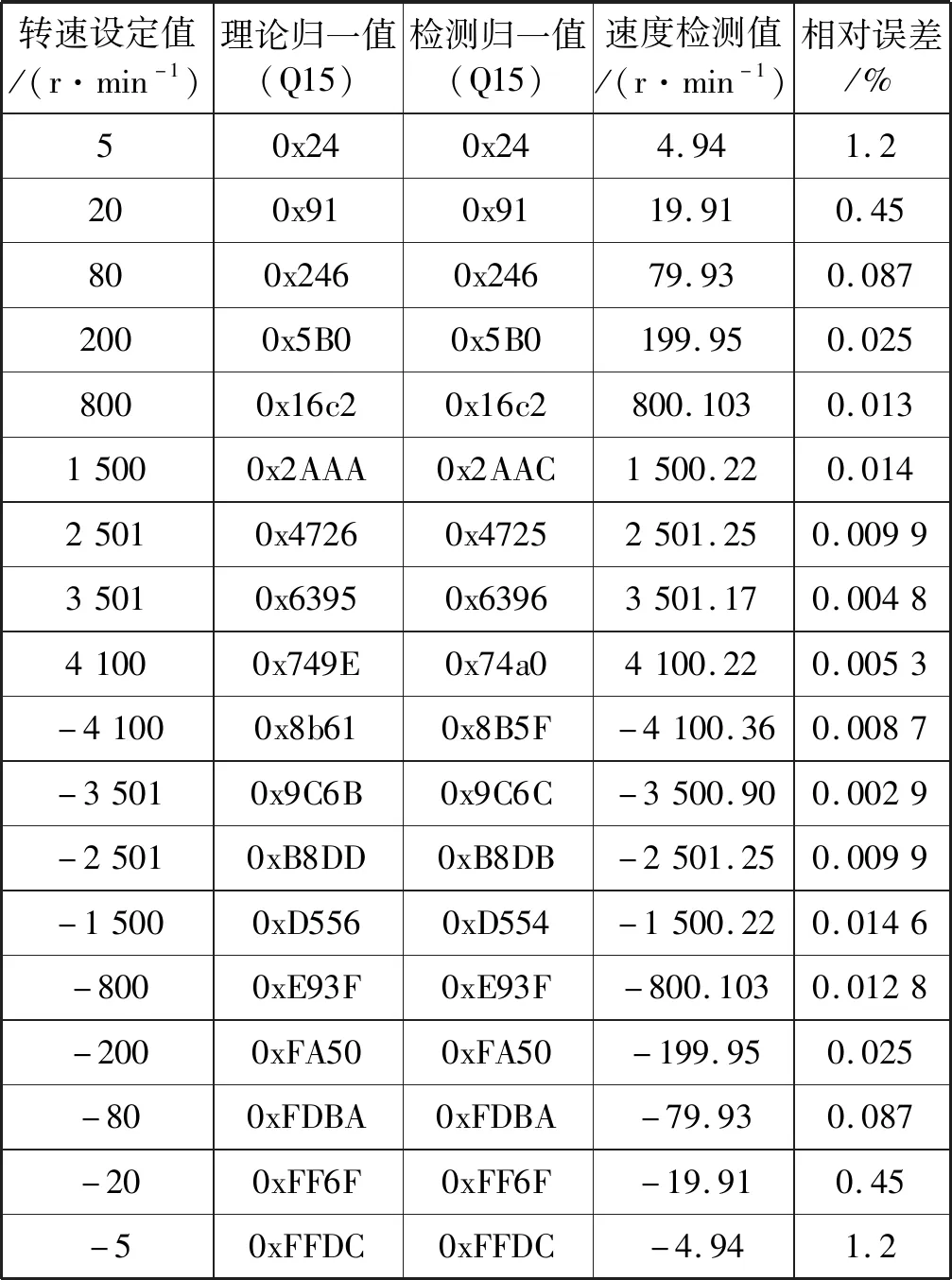
表2 实验仿真结果

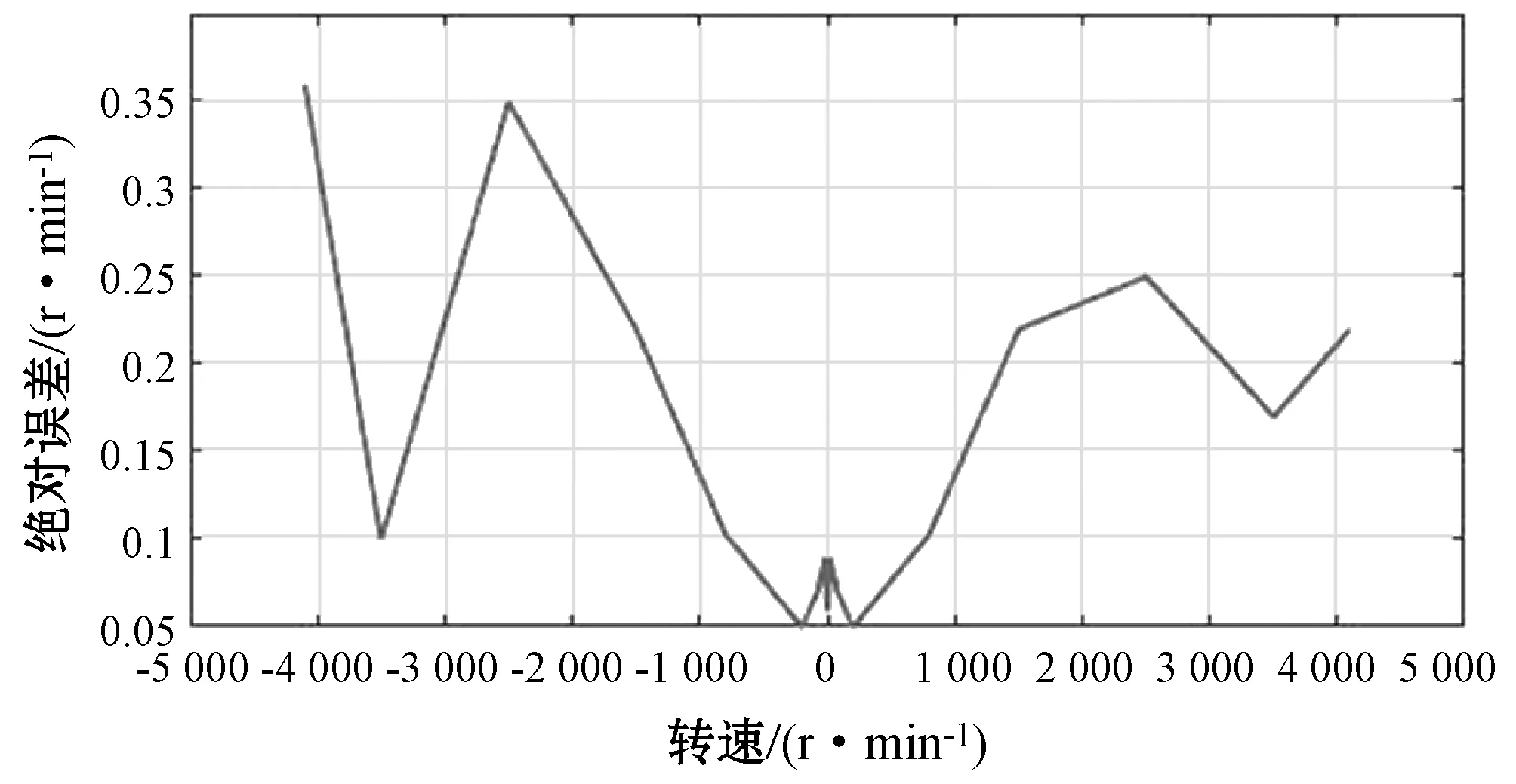
图6 绝对误差统计图

从仿真结果来看，以归一值表示时测量误差在±2范围之内，且在低速时有较高的准确度。转速测量值误差最大不超过±0.4 r/min，而在低速范围-200～200 r/min内，绝对误差不超过0.1 r/min。误差的存在主要由于：

(1) 归一化量化误差。归一化由于采用定点数，故在进行转换时会引入一定误差，误差范围在：

(2) 由于定点化的实现方式,FPGA在运算过程中会存在位宽截取情况，引入一定误差。

变M/T归一化测速算法及普通M/T测速算法(取M1值为128)不同转速下的响应时间对比结果如图7所示。

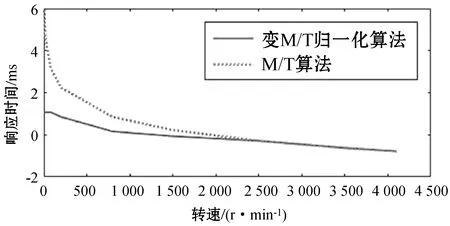
图7 响应时间对比对数图

根据图7对比，当电机处于低速运行时，变M/T归一化算法在响应时间上相比于M/T算法有极大的缩减，当转速低于50 r/min时响应时间能缩短25倍以上。这对于电机在低速运行时提高系统的灵敏度有极大的改善和帮助。

5 结 语

本文针对伺服电机的测速问题提出了一种基于FPGA的变M/T归一化测速算法。通过实验仿真表明，该算法无论在低速范围内还是高速范围内均有较高的测速精度，同时具有快速响应的特点。归一化的设计使得算法能够针对不同参数型号编码器及永磁同步电机均能有较高的测量精度，也广泛适用于伺服电机控制系统中的速度控制应用，避免因不同变量的单位数制问题引入的计算精度与计算误差。同时Booth算法的引入也极大降低了算法对DSP的依赖性。本文算法为空间材料科学实验装置中永磁同步电机的速度检测方式提供了一种参考设计思路。